R言語の紹介

はじめに

• 「ビッグテータ」に関心をもち「ビッグテータのデータ解析手法」をインターネットで調べる．
• データ解析言語R(R言語)を知る．

R言語とは

R言語（あーるげんご）はオープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境である。
R言語はニュージーランドのオークランド大学のRoss IhakaとRobert Clifford Gentlemanにより作られた。現在ではR Development Core Team（S言語開発者であるJohn M. Chambersも参画している[1]。）によりメンテナンスと拡張がなされている。
なお、R言語の仕様を実装した処理系の呼称名はプロジェクトを支援するフリーソフトウェア財団によれば『GNU R』である[2]が、他の実装形態が存在しないために日本語での慣用的呼称に倣って、当記事では、仕様・実装を纏めて適宜にR言語や単にR等と呼ぶ。 (Wikipediaより引用)

R言語の仕様

概要

  ＊＊＊＊＊＊＊ R (統計電卓）＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
  準備: # comment,  options(echo=F):非表示, system("ls")
  定数：pi, exp(1), ヘルプ：?plot, apropos("read")
  ライブラリ： source("RLIB"), library(xtable),
  例: x <- c(1,2,3); mean(x); var(x); length(x),stem(x); q();
  分布: 密度 dnorm(x),下側確率 pnorm(x),%点 qnorm(p), 乱数 rnorm(n)
  作図：plot(c(1,2,3),c(11,12,13)); curve(sin(x),0,4*pi);
  ソート: sort(a), order(a), unique(a), duplicate(a)
  方程式：solve(A, c(b1,b2)) <--- A x = b
  行列：A <- matrix(c(11,12,21,22), ncol=2, byrow=T)
        diag(c(11,22)), t(A), solve(A), eigen(A), svd(A)
        rbind(A,B), cbind(A, B), rep(x,n)
  ファイル：sink("out");  ... sink();
  ユーザ関数：ls(), 関数定義：関数名,　ライブラリ一覧: library()  
  ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊(T.INOUE)＊＊

定数

--- const : 定数 -------------------------------------------------------
   pi        : 円周率,                exp(1)     : 自然対数の底
   LETTERS   : アルファベット大文字   letters    : アルファベット小文字
   month.abb : 月の英語略号           month.name : 月の英語名
   TRUE (T)  : 真(論理値)             FALSE (F)  : 偽(論理値)
   NA        : 数値の欠側値           NaN        : 非数値の欠側値
   NULL      : 未定義                 Inf        : 無限大

   + (和),  - (差),  * (積),  / (商),  %% (x mod y),  ^ (巾乗),  
   %/% (整数商)   %o% (外積)
------------------------------------------------------------------------

基本関数

● 三角関数ファミリー(引数の単位はラディアンでベクトル化されている)
   cos(x)  sin(x)  tan(x)  acos(x)   asin(x)  atan(x)   atan2(y, x)
● hyperbolic 関数ファミリー  [cosh(x) = (exp(x) + exp(-x))/2]
   cosh(x)  sinh(x)  tanh(x)   acosh(x)  asinh(x)  atanh(x)   
● 対数，指数関数ファミリー(底 base は実数．引数 x は実数もしくは複素数)
   log(x, base = exp(1))   底 base (既定値 exp(1)) の対数
   log10(x)        常用対数 log(x, base=10)
   log2(x)         底 2 の対数
   exp(x)          指数関数
● 組合せ論的関数
    * choose(n, k) n 個から k 個を取り出す場合の数
    * lchoose(n, k) choose(n,k) の自然対数
    * factorial(x) x の階乗 x! (R 1.9 より登場．実際は単に gamma(x+1) を
      計算するだけで，整数でない x も可能)
● その他の組込み関数(符号，絶対値，平方根)
    * sign(x) 実数 x の符号．x > 0, = 0, x <0 に応じて sign(x) = -1,0,1
    * abs(x) 実数もしくは複素数 x の絶対値
    * sqrt(x) 整数の平方根，もしくは複素数の平方根(主値)
● 数値ベクトルに対する逐次処理関数
    * cumsum(x) 累積和ベクトルを返す
    * cumprod(x) 逐次積ベクトルを返す
    * cummax(x) 逐次最大値ベクトルを返す
    * cummin(x) 逐次最小値ベクトルを返す
●  ガンマ関数ファミリー，確率分布関数，統計関数，作図関数，等は後で示す．

データの並び(ベクトル)の生成

c(10,30,20)              # > より右が入力部分を示す．結果は[1]の後の部分

## [1] 10 30 20

10:30                    # 初期値10，終値30，増分1の数列

##  [1] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

seq(10,30,by=5)          # 初期値10，終値30，増分5の数列

## [1] 10 15 20 25 30

seq(10,30,length=11)     # 区間[10,30]を10等分する分点列

##  [1] 10 12 14 16 18 20 22 24 26 28 30

x <- 10:30               # ベクトルxの定義 (<- は付値記号と呼ばれる)
x[2]; x[2:5]; x[-(2:5)]  # ベクトルxの部分の取り出し

## [1] 11

## [1] 11 12 13 14

##  [1] 10 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

--- vect : ベクトルのメモ------------------------------------------------
   x <- c(1,3,2)
   length(x) # ベクトルxの大きさ(長さ)
   a:b    # a から始まり(b を越えない)公差 1 (または -1) の等差数列
   seq(a, b, by = c) # a から始まり(b を越えない)公差 c の等差数列
   seq(a, b, length = n) # a, b 間を n 等分する等差数列
   rep(x, n) # x を n 回繰り返したベクトル
   numeric(n) # 0 を n 個並べたベクトル
   sequence(3)   ---> 1 2 3
   sequence(3:1) ---> 1 2 3  1 2  1   # sequence(c(3,2,1)) の意味
   sequence(1:3) ---> 1  1 2  1 2 3   # sequence(c(1,2,3)) の意味
 ベクトルの一部を取り出す
    x[2:5]    # x[2], x[3], ..., x[5] を取り出す，x[c(2,3,4,5)] でも良い
    x[-2:5]   # x[2], x[3], ..., x[5] 以外を取り出す
    head(x), head(x,n=10)         # 既定では最初の6要素, 10要素
    tail(x, n=10)                 # 最後の10要素
 ベクトルの一部を取り除く
    x <- 1:9;  x[-2, -3, -5]             # x[2], x[3], x[5] を取り除く
 ベクトルの一部を置き換える
    x=1:10;  y=c(2,5,10);  z=c(12,15,20)
    w=replace(x,y,z) # xのyで指定される添字箇所をzの要素で置き換える
    w <- replace(x,y,NA) # 上記zの代わりにNAで置き換える
        ---> [1]  1 NA  3  4 NA  6  7  8  9 NA
    replace(w,which(is.na(w)),0) # wの中のNAを0で置き換える
        ---> [1] 1 0 3 4 0 6 7 8 9 0
 ベクトルの要素がある条件を満たすような添字を取り出す
   x <- c(0.1, 0.7, 0.2, 0.6, 0.3)
   y <- which(x < 0.5)  # 0.5 未満以の値を持つ要素の添字を取り出す
   y  ---> [1]  1  3  5 
   x[y]    # 0.5 未満以の値を持つ要素を取り出す，x[x < 0.5] と同じ
   注意！　xにNAが入っているとx[x < 0.5] とx[which(x < 0.5)]は異なる．
      x=c(-Inf,1,2,3,NA,NaN,5,6, Inf)
      x[x<4]        ---> [1] -Inf    1    2    3   NA   NA
      x[which(x<5)] ---> [1] -Inf    1    2    3
-----------------------------------------------------------------------

行列演算

(A <- matrix(c(1,2, 3,4),2,2,byrow=T)) # (2x2)行列Aの定義

##      [,1] [,2]
## [1,]    1    2
## [2,]    3    4

(b <- matrix(c(4,10),2,1))              # (2x1)ベクトルbの定義

##      [,1]
## [1,]    4
## [2,]   10

dim(A); dim(b)                         # 次元数確認

## [1] 2 2

## [1] 2 1

solve(A,b)                       # A x = b を(ベクトルxについて)解く

##      [,1]
## [1,]    2
## [2,]    1

solve(A)                         # Aの逆行列を求める

##      [,1] [,2]
## [1,] -2.0  1.0
## [2,]  1.5 -0.5

その他の行列操作:
　　diag(c(1,2,3),3,3)  # (3x3)対角行列
　　A <- rbind(c(1,2,3),c(4,5,6)) # (2x3)行列
　　A <- cbind(c(1,2,3),c(4,5,6)) # (3x2)行列
　　A %*% B # 行列の積，t(A) : 転置行列，solve(A) : 逆行列，
　　det(A) : 行列式，　eigen(A) : 固有値分解，　svd(A) : 特異値分解

#　逆行列が存在しない場合の例
(A <- matrix(c(1,2,3, 4,5,6, 7,8,9), 3,3, byrow=T))

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

det(A)   # 行列式の値は0より，逆行列は存在しない

## [1] 6.661338e-16

try( solve(A) )  # エラー終了を回避する

## Error in solve.default(A) : 
##    システムは数値的に特異です: 条件数の逆数 = 1.54198e-18

データの並びとソート,順位

x <- c(20,40,30,10)   # 4個のデータの並びを(ベクトル)xとする
sort(x)               # 昇順に並び換えた結果を返す

## [1] 10 20 30 40

order(x)              # 昇順順位の個体番号（データ位置）を返す

## [1] 4 1 3 2

                      #     (第1順位データは4番目)
rank(x)               # 個体番号の昇順順位を返す(20は第2順位である)

## [1] 2 4 3 1

x[c(1,3)]             # x から1番目と3番めのデータを取り出す

## [1] 20 30

ox <- order(x); x[ox] # ox を添字ベクトルとするデータ(間接指定)

## [1] 10 20 30 40

rev(x)                # xを逆順に並べた結果

## [1] 10 30 40 20

統計関数

多くの場合，総称関数として作用し，多変量データ，時系列データにも使える．
  * max(..., na.rm=FALSE)       最大値
  * min(..., na.rm=FALSE)       最小値
  * range(..., na.rm = FALSE)   範囲
  * mean(x, ...)                平均
  * weighted.mean(x, w)         重み付平均
  * median(x, na.rm=FALSE)      メディアン(中央値)
  * quantile(x, probs = seq(0, 1, 0.25),na.rm =FALSE, ...)  パーセント点
  * fivenum(x, na.rm = TRUE)    Tukey統計値
  * IQR(x)                      四分位範囲(Interquartile Range)
  * mad(x)                      中央値絶対偏差(median absolute deviation)
  * var(x, y = NULL)            分散(不偏分散)  共分散も可

  * sd(x, na.rm = FALSE)        標準偏差
  * cor(x, y = NULL)            相関係数
  * cov(x, y = NULL)            共分散

  * table(x)                    集計表
  * cut(x,breaks,right=T)       度数集計

  * sum(x)                      総和
  * prod(x)                     総積
  * cumsum(x)                   累積和

  * rowSums  rowMeans           各行ごとの和   行ごとの平均
  * colSums  colMeans           各列ごとの和   列ごとの平均

  * diff(x, lag=1, dfference=1, ...)   階差

  * scale(X)                           標準化変換(平均，標準偏差による) 
  * scale(X,scale=F)                   平均を原点とする変換

x <- c(10,20,30)         # 3個のデータをベクトルxとする
min(x); max(x)           # 最小値，最大値を求める

## [1] 10

## [1] 30

mean(x); var(x); sd(x)   # 平均，分散(不偏分散)，標準偏差を求める

## [1] 20

## [1] 100

## [1] 10

str(scale(x))                 # 平均と標準偏差に基づく標準化変換を行う

##  num [1:3, 1] -1 0 1
##  - attr(*, "scaled:center")= num 20
##  - attr(*, "scaled:scale")= num 10

確率分布

    (d***：確率密度，p***：分布関数値，q***：パーセント点，r***：乱数)
    2項：binom(x,n,p),              ポアソン：pois(x,lam)，
    負の2項：nbinom(x,n,p)          幾何：geom(x,p)，    
    超幾何 : hyper(x,m,n,k)，       *離散一様: DU(x,x0,dx,x1)
    一様：unif(x,a,b)，             指数：exp(x,lam)，
    正規：norm(x,mu,sd),            コーシー：cauchy(x,mu,s)， 
    ガンマ：gamma(x,a,rate=1/s)，   ベータ：beta(x,a,b)，
    対数正規：lnorm(x,mu,sigma)，   ワイブル：weibull(x,shape,scale=1)，
    ロジスティック：logis(x,loc=0,scale=1)，
    t：t(x,df,ncp=0)，              カイ2乗：chisq(x,df,ncp=0)，
    F：f(x,df1,df2),                
    *混合正規分布:normmix(x.mu1,sd1,mu2,sd2,p)
    *2変量正規分布：dnorm2(x,y,means=c(0,0),sds=c(1,1),cor=0)
    *多変量正規分布に従う乱数生成 : mk.mvd(n,av,sd,R,seed=1,round=F)

確率分布と乱数

options(width=60,dights=4)
dnorm(0,0,1)   # 正規分布N(0,1^2)の0における確率密度

## [1] 0.3989423

pnorm(0,0,1)   # 正規分布N(0,1^2)の0における分布関数値(P{X < 0})

## [1] 0.5

1 - pnorm(c(0,1,2,3),0,1)   # 上側確率 P{X > x}

## [1] 0.500000000 0.158655254 0.022750132 0.001349898

c(1/2, 1/6, 1/44, 1/1000)   # 上記の上側確率に近い分数 

## [1] 0.50000000 0.16666667 0.02272727 0.00100000

qnorm(0.5,0,1) # 正規分布N(0,1^2)の50%点(P{X < x0}=0.5 となるx0の値)

## [1] 0

rnorm(10,0,1)  # N(0,1^2)に従う確率変数の実現値(正規乱数)を10個生成

##  [1] -0.26833282 -0.74244654  0.63939834  1.38297166
##  [5]  1.53611517  0.28488036  0.76007271 -0.04007211
##  [9]  0.28415353  0.86844364

set.seed(1)                  # 乱数の初期値を設定
x <- rnorm(10000,0,1)        # N(0,1^2)に従う乱数を10000個生成する
out <- hist(x,freq=F,xlim=c(-4,4))  # データxのヒストグラムを描画する 
par(new=T)                   # 図を上書きする
dens <- function(x){dnorm(x,mean=0,sd=1)} 
   # N(0,1^2)の密度関数を関数densとする(dnormは3変数関数であるため)
curve(dens,xlim=c(-4,4),col="red",add=T) # 関数densを上書き描画する

out      # ヒストグラム(度数分布表)の詳細

## $breaks
##  [1] -4.0 -3.5 -3.0 -2.5 -2.0 -1.5 -1.0 -0.5  0.0  0.5  1.0
## [12]  1.5  2.0  2.5  3.0  3.5  4.0
## 
## $counts
##  [1]    2   16   59  182  444  904 1490 1971 1864 1432  955
## [12]  438  193   40    7    3
## 
## $density
##  [1] 0.0004 0.0032 0.0118 0.0364 0.0888 0.1808 0.2980 0.3942
##  [9] 0.3728 0.2864 0.1910 0.0876 0.0386 0.0080 0.0014 0.0006
## 
## $mids
##  [1] -3.75 -3.25 -2.75 -2.25 -1.75 -1.25 -0.75 -0.25  0.25
## [10]  0.75  1.25  1.75  2.25  2.75  3.25  3.75
## 
## $xname
## [1] "x"
## 
## $equidist
## [1] TRUE
## 
## attr(,"class")
## [1] "histogram"

正規分布 \(X \sim N(\mu,\,\sigma^2)\) の確率密度関数\(f(x)\): \[ f(x) = \frac{1}{\sqrt{2\,\pi\,\sigma^2}}\,e^{-\,\frac{(x-\mu)^2}{2\,\sigma^2}}\]

R言語に基づくデータ解析例

options(width=60); source("/home/inoue/r-ex/RLIB")
# CSVファイルから読み込み
X0 <- read.csv("/home/inoue/r-ex/dex2.csv",header=T) 
head(X0,3); tail(X0,3)　　# 内容確認

##   No. 英語 数学 国語 社会
## 1   1   50   62   54   52
## 2   2   36   30   56   53
## 3   3   48   44   59   74

##    No. 英語 数学 国語 社会
## 38  38   47   65   67   65
## 39  39   45   48   63   75
## 40  40   35   35   62   75

df <- data.frame(X0[,-1]) # 第1カラムを除いてデータフレーム化
str(df)                   # データフレームdfの属性表示

## 'data.frame':    40 obs. of  4 variables:
##  $ 英語: int  50 36 48 50 40 46 45 76 62 43 ...
##  $ 数学: int  62 30 44 28 43 40 28 78 68 48 ...
##  $ 国語: int  54 56 59 53 66 51 75 70 58 69 ...
##  $ 社会: int  52 53 74 63 77 65 74 89 57 75 ...

head(df,3); tail(df,3)    # 最初の３例，最後の３例を表示

##   英語 数学 国語 社会
## 1   50   62   54   52
## 2   36   30   56   53
## 3   48   44   59   74

##    英語 数学 国語 社会
## 38   47   65   67   65
## 39   45   48   63   75
## 40   35   35   62   75

apply(df,2,mean)          # 変量毎の平均を求める

##   英語   数学   国語   社会 
## 49.725 49.550 60.950 65.575

var(df)                   # 分散・共分散行列を求める

##            英語        数学       国語       社会
## 英語  99.332692 106.8217949 20.0884615   2.905769
## 数学 106.821795 223.8948718  0.2589744 -31.862821
## 国語  20.088462   0.2589744 98.6641026  58.029487
## 社会   2.905769 -31.8628205 58.0294872 101.173718

apply(df,2,sd)            # 変量毎の標準偏差を求める

##      英語      数学      国語      社会 
##  9.966579 14.963117  9.932981 10.058515

cor(df)                   # 相関行列を求める

##            英語         数学        国語        社会
## 英語 1.00000000  0.716294628 0.202918195  0.02898552
## 数学 0.71629463  1.000000000 0.001742429 -0.21170362
## 国語 0.20291819  0.001742429 1.000000000  0.58081161
## 社会 0.02898552 -0.211703622 0.580811615  1.00000000

par(family="Japan1")
par(mfrow=c(2,2),cex=0.6)                  # 2x2の作図領域を確保
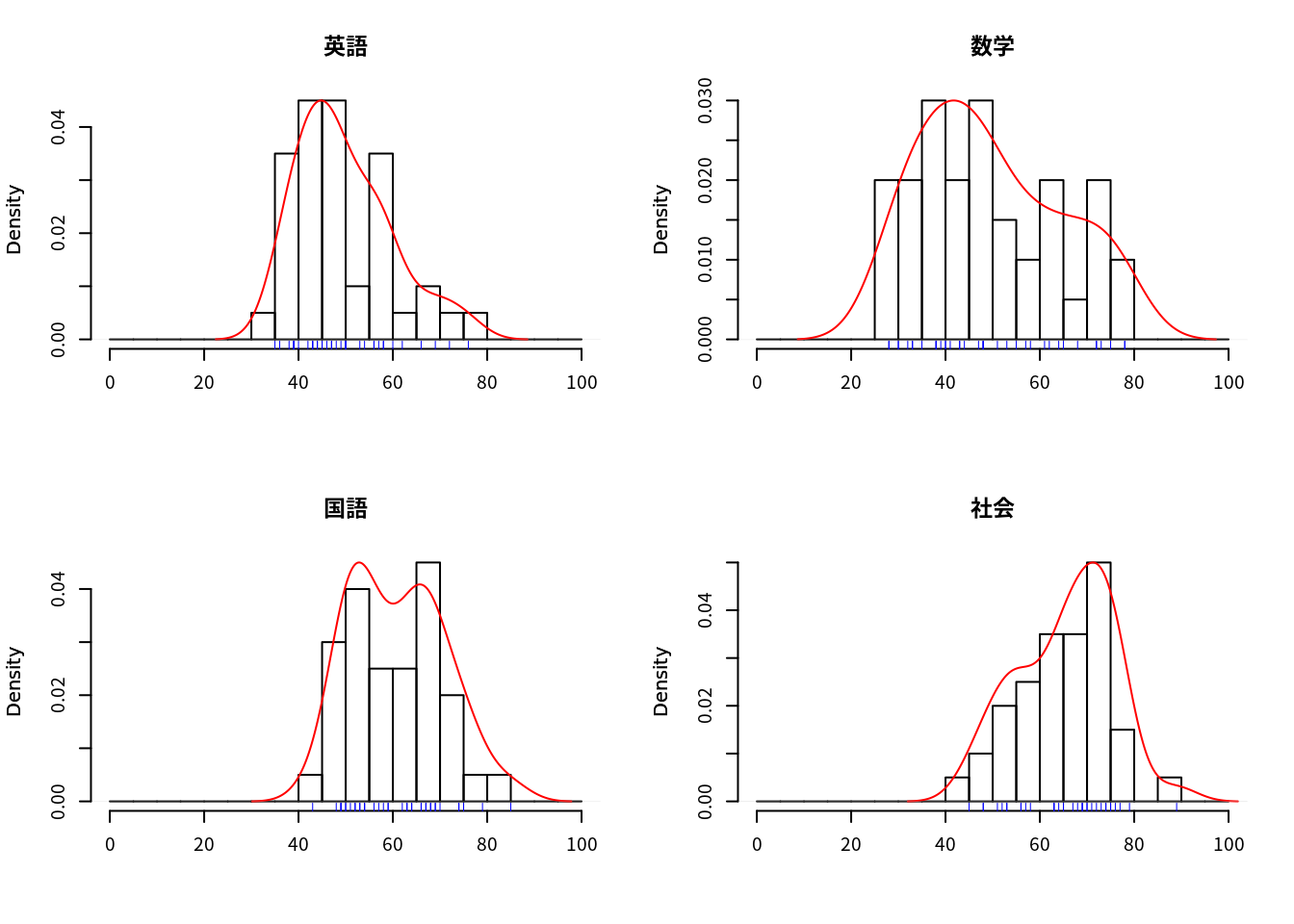
colnames(df)

## [1] "英語" "数学" "国語" "社会"

for (j in 1:ncol(df)) {                    # 変量毎のヒストグラム
  hist(df[,j],xlim=c(0,100),freq=F,breaks=seq(0,100,5),
       main=colnames(df[j]),xlab="") 
  par(new=T);                              # 推定密度関数の重ね書き
  plot(density(df[,j]),xlim=c(0,100),col="red",main="",xlab="",axes=F)
  rug(df[,j],col="blue")                   # データ点の描画を追記
  }

par(family="Japan1",pty="s",omd=c(0,1,0,1)); 
pairs(scale(df),xlim=c(-3.1,3.1),ylim=c(-3.1,3.1),cex=0.3)  # 対散布図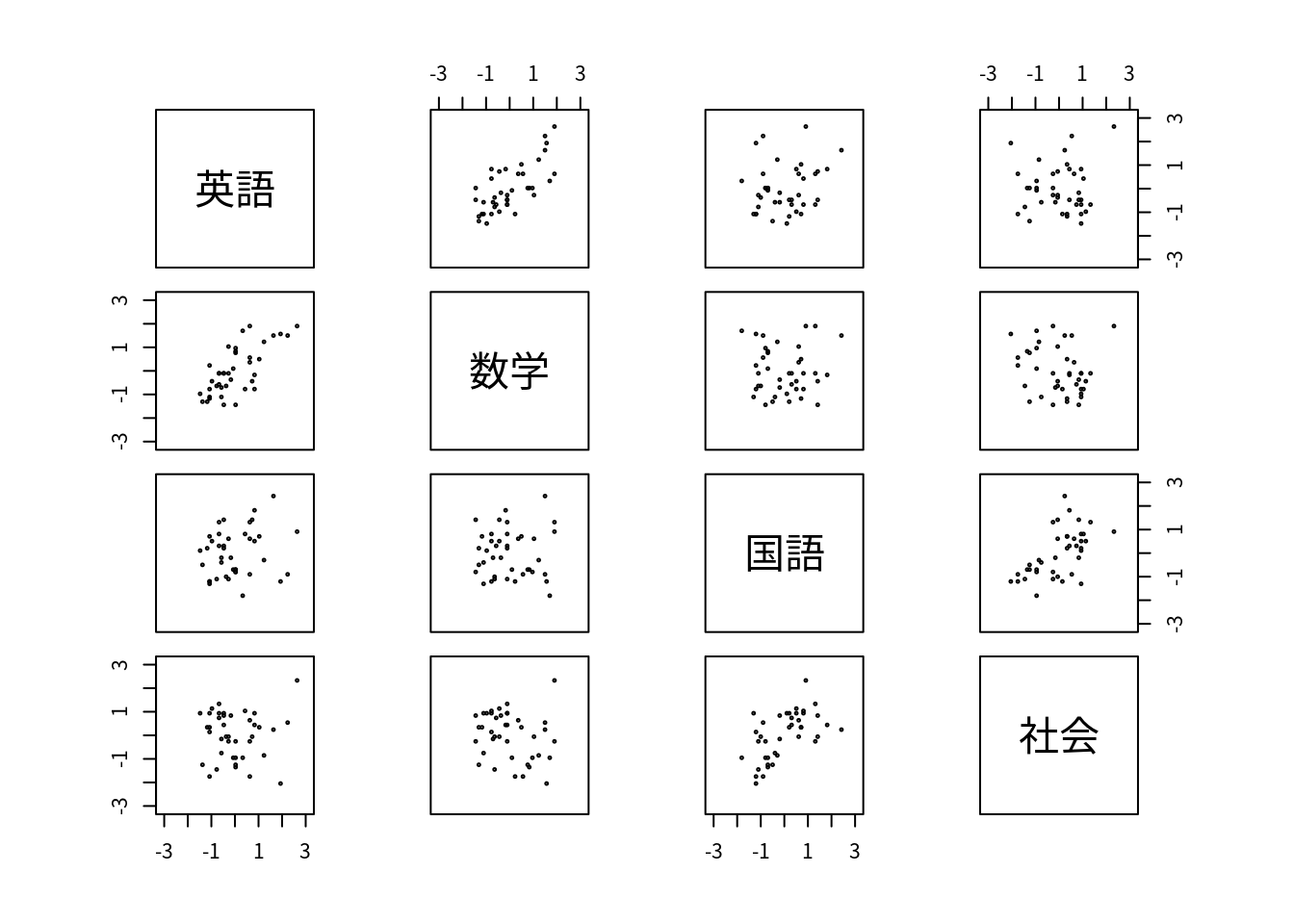 

par(family="Japan1"); pairs1(df)           # 私用ライブラリの利用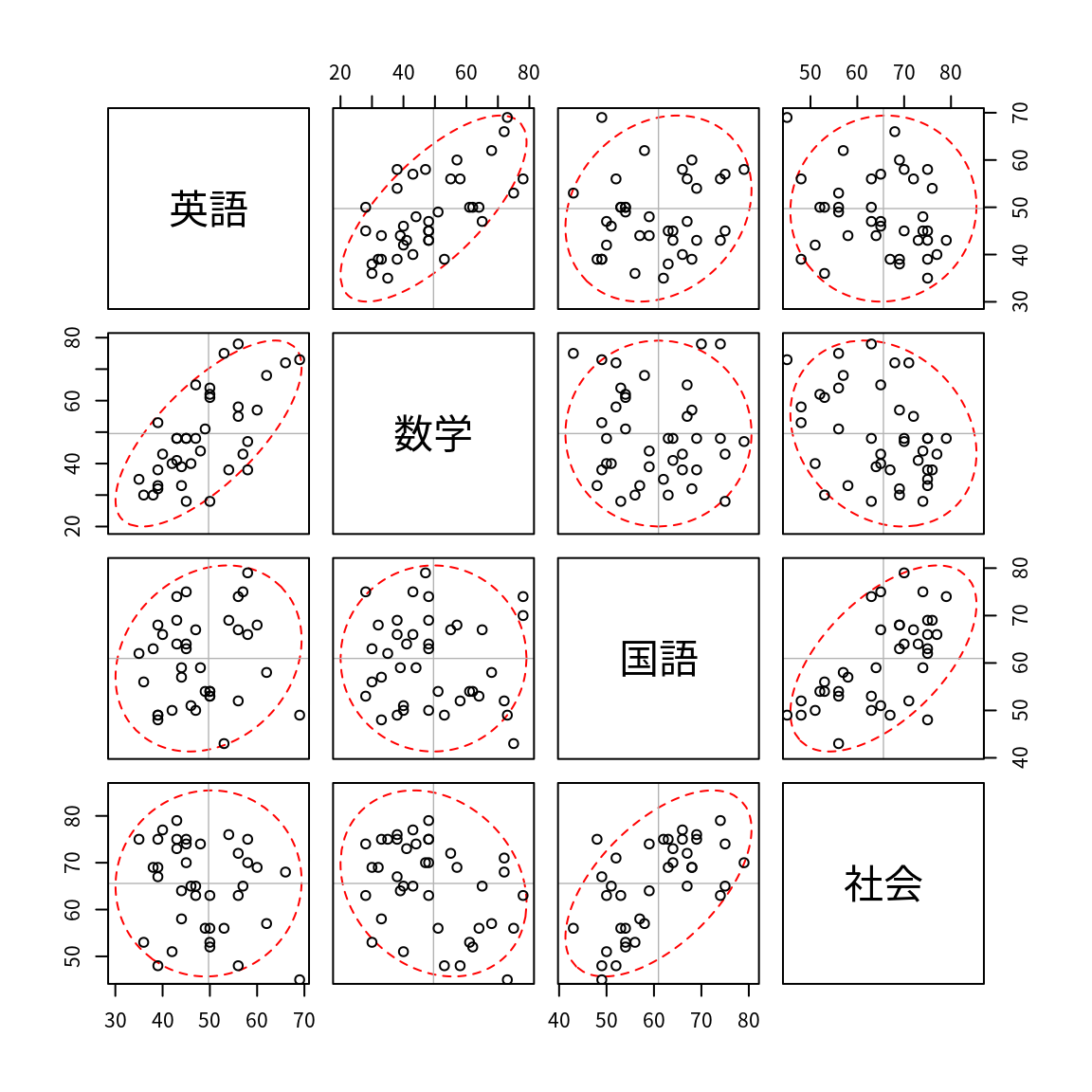

par(family="Japan1"); 
boxplot(df,main="箱ひげ図(四分位数）")      # 箱ひげ図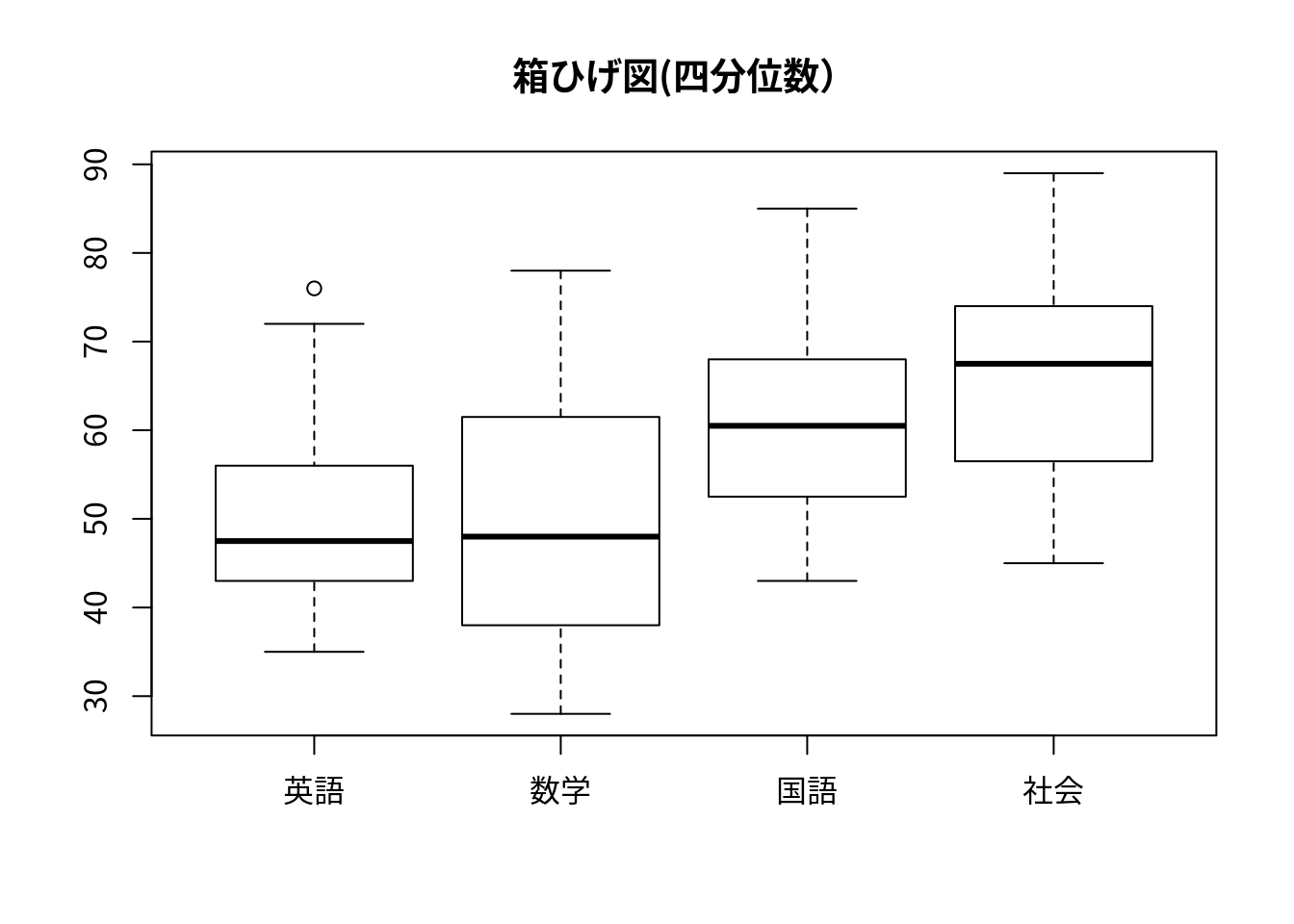

主成分分析，クラスタ分析，因子分析

prc <- prcomp(scale(df))                  # 主成分分析
summary(prc)

## Importance of components:
##                           PC1    PC2     PC3     PC4
## Standard deviation     1.3211 1.2715 0.62717 0.49459
## Proportion of Variance 0.4364 0.4042 0.09834 0.06115
## Cumulative Proportion  0.4364 0.8405 0.93885 1.00000

par(family="Japan1"); 
hc <- hclust(dist(scale(df)))
plot(hc,xlab="")                # クラスタ分析(デンドログラム)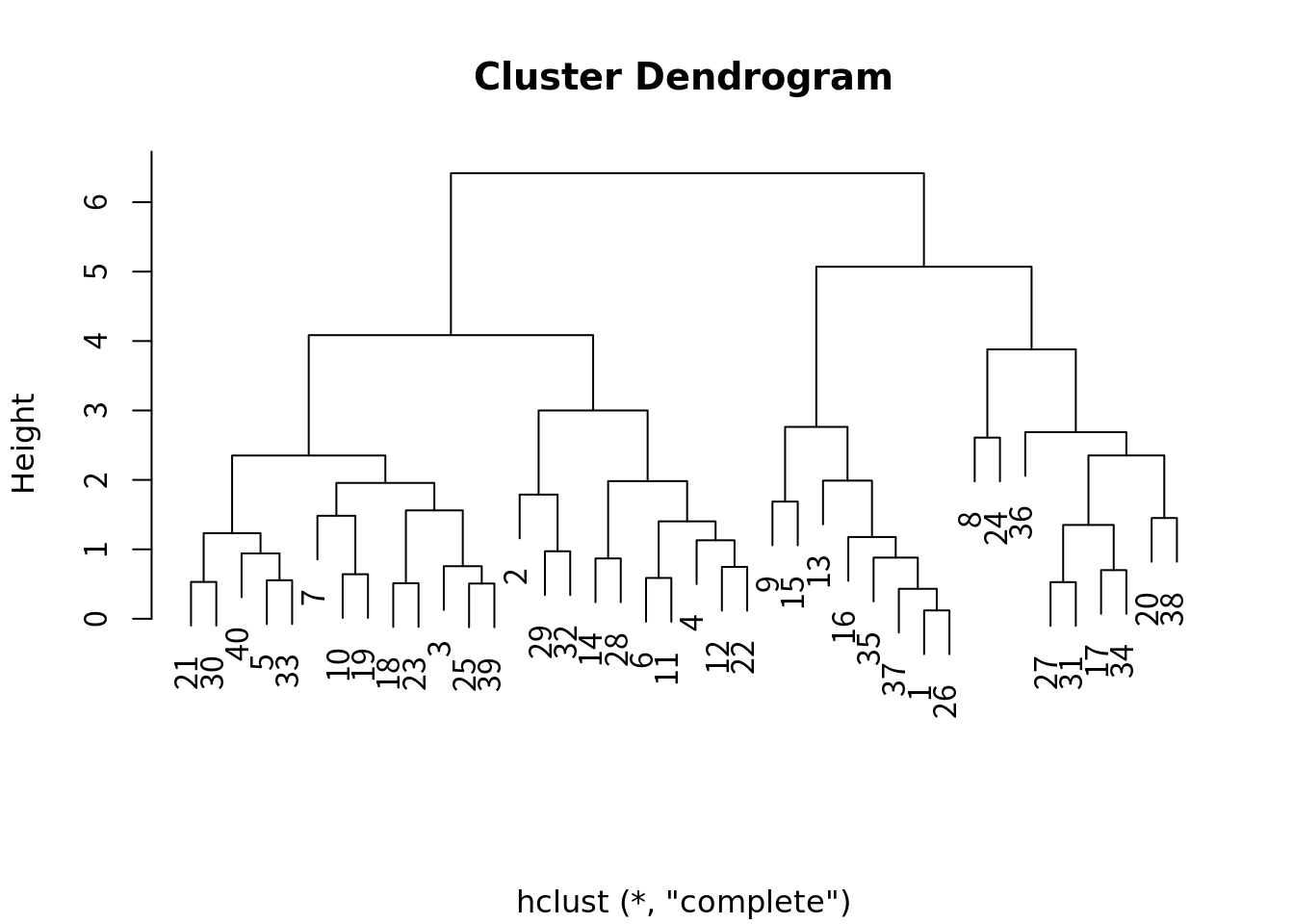

df[c(21,22,9,38),]

##    英語 数学 国語 社会
## 21   39   32   68   69
## 22   44   39   59   64
## 9    62   68   58   57
## 38   47   65   67   65

scale(df)[c(21,22,9,38),]

##            英語      数学       国語       社会
## [1,] -1.0760964 -1.172884  0.7097568  0.3405075
## [2,] -0.5744198 -0.705067 -0.1963157 -0.1565838
## [3,]  1.2316162  1.233032 -0.2969904 -0.8525116
## [4,] -0.2734138  1.032539  0.6090820 -0.0571655

pca1 <- pca(scale(df))                   # 主成分分析(因子分析)
#summary(pca1)
### 私用関数 pca.fig を定義する
pca.fig <- function(pca, label=c("x1","x2","x3","x4"), ...) { 
  opar <- par(mfrow = c(1, 2),pty="s",cex=0.8);  
  first <-  pca1$factor[,1];  second <-  pca1$factor[,2]
  plot(first, second,  type="n", xlim=c(-1.1,1.1),ylim=c(-1.1,1.1),
      main="因子負荷", cex=0.6)
  abline(h=0); abline(v=0)
  text(first, second, label=label,cex=0.8)
  z1 <- -1 * pca$Zstandard[,1]
  z2 <- -1 * pca$Zstandard[,2]
  plot(z1, z2, type="n", 
       main="(標準化)主成分スコア",cex=0.6)
       abline(h=0); abline(v=0)
  text(z1, z2, label=1:length(z1),cex=0.8)
} # end of pca.fig

par(family="Japan1")
pca.fig(pca1,label=colnames(df))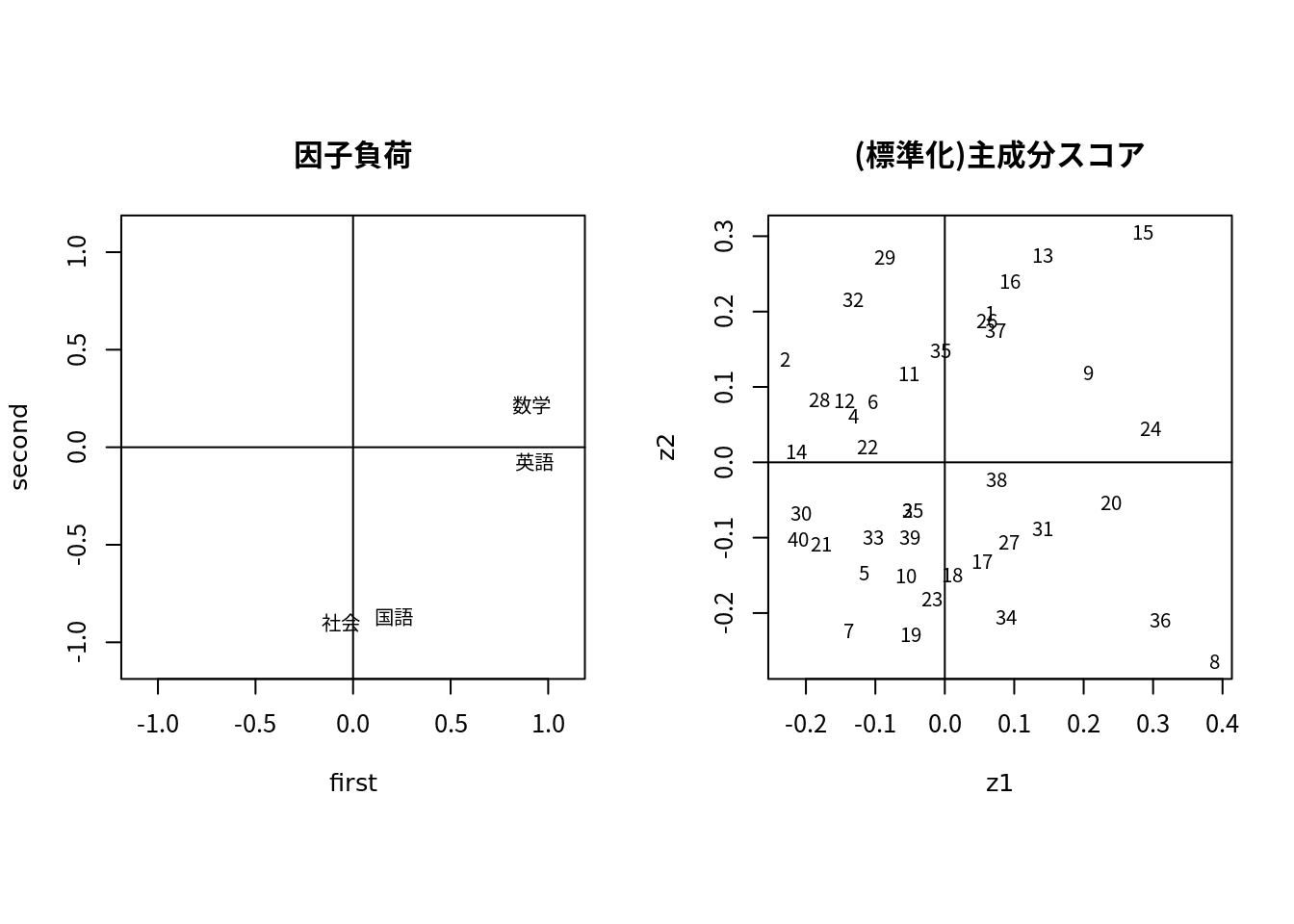

Z <- scale(df); Z[c(8,15,24,19),]

##            英語      数学       国語      社会
## [1,]  2.6363109  1.901342  0.9111062  2.328873
## [2,]  1.9339635  1.567187 -1.2030629 -2.045531
## [3,]  2.2349695  1.500356 -0.9010387  0.539344
## [4,] -0.6747551 -0.103588  1.3138050  1.334690

直線の当てはめ(最小2乗法)

直線の当てはめ問題をR言語を用いて処理する例を示す.関数lsfit()の出力の内 の coefficients(回帰係数)より,モデル \(y = \beta_0 + \beta_1\,x\) の回帰係数 \(\beta_0=-3.4, \, \beta_1=2\) を得る.また,データ \((x,y)\) のプロット,回帰式の作図を示す.

x <- c(3,4,5,6,7)   # データｘ
y <- c(2,6,6,8,11)  # データｙ
out <- lsfit(x,y)   # 関数lsfit()を利用してy=b0+b1*x(直線)を当てはめる
str(out)            # 結果の簡略表示

## List of 4
##  $ coefficients: Named num [1:2] -3.4 2
##   ..- attr(*, "names")= chr [1:2] "Intercept" "X"
##  $ residuals   : num [1:5] -0.6 1.4 -0.6 -0.6 0.4
##  $ intercept   : logi TRUE
##  $ qr          :List of 6
##   ..$ qt   : num [1:5] -14.758 6.325 -0.138 0.309 1.757
##   ..$ qr   : num [1:5, 1:2] -2.236 0.447 0.447 0.447 0.447 ...
##   .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..$ : NULL
##   .. .. ..$ : chr [1:2] "Intercept" "X"
##   ..$ qraux: num [1:2] 1.45 1.12
##   ..$ rank : int 2
##   ..$ pivot: int [1:2] 1 2
##   ..$ tol  : num 1e-07
##   ..- attr(*, "class")= chr "qr"

out$coefficients    # 回帰係数のみを表示

## Intercept         X 
##      -3.4       2.0

plot(x,y)           # データ点(x,y)を作図
abline(out,col=2)   # 推定直線を赤(col=2)で表示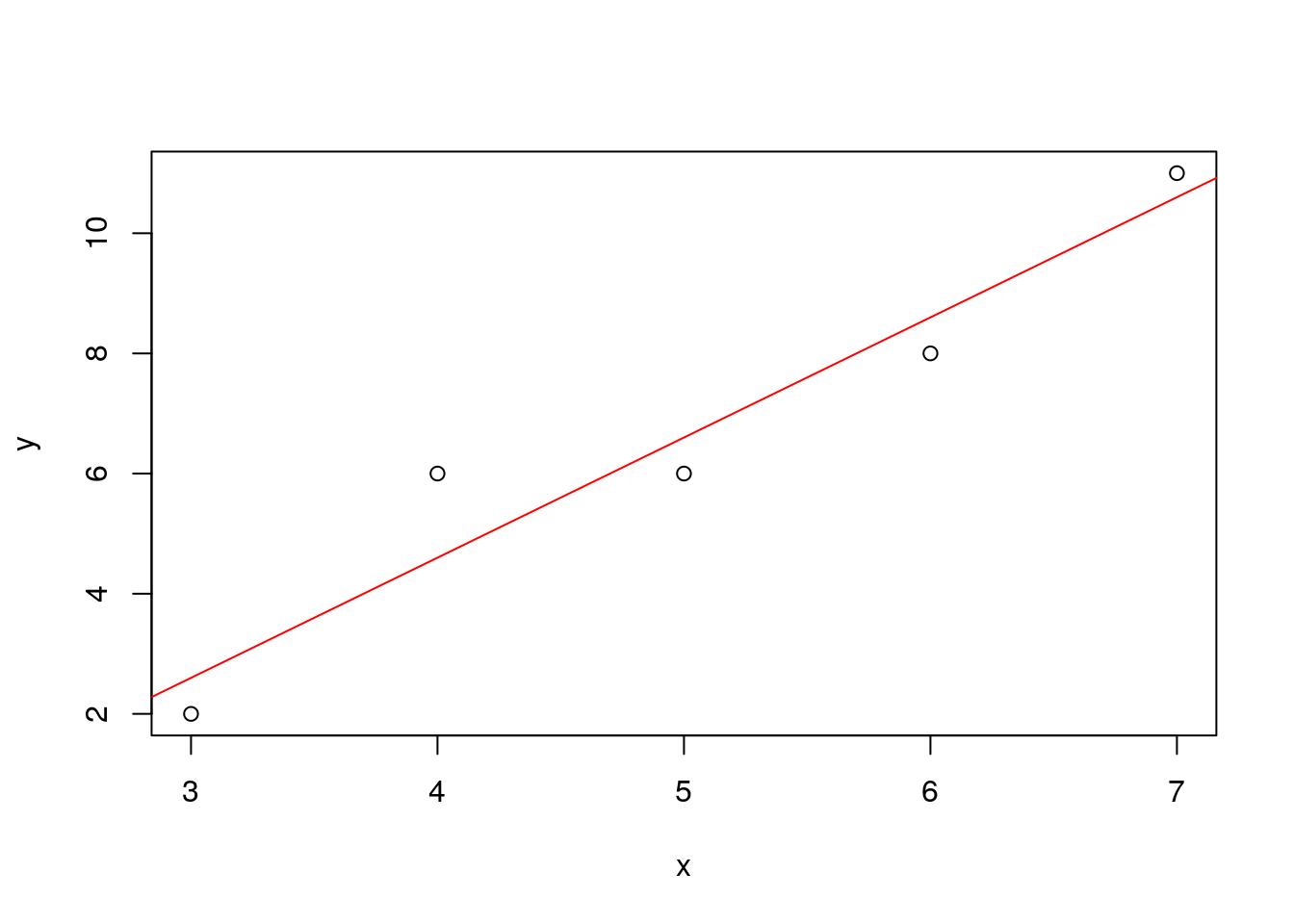

次に，原点を通る直線\(y = \beta_1 \,x\) を当てはめる場合の結果を示す．

out <- lsfit(x,y,intercept=FALSE)  # y=b1*x(原点を通る直線)を当てはめる
out$coefficients                   # 回帰係数のみを表示

##       X 
## 1.37037

plot(x,y,xlim=c(0,7),ylim=c(0,11)) # データ点(x,y)を作図
abline(out,col=2)                  # 推定直線を赤(col=2)で表示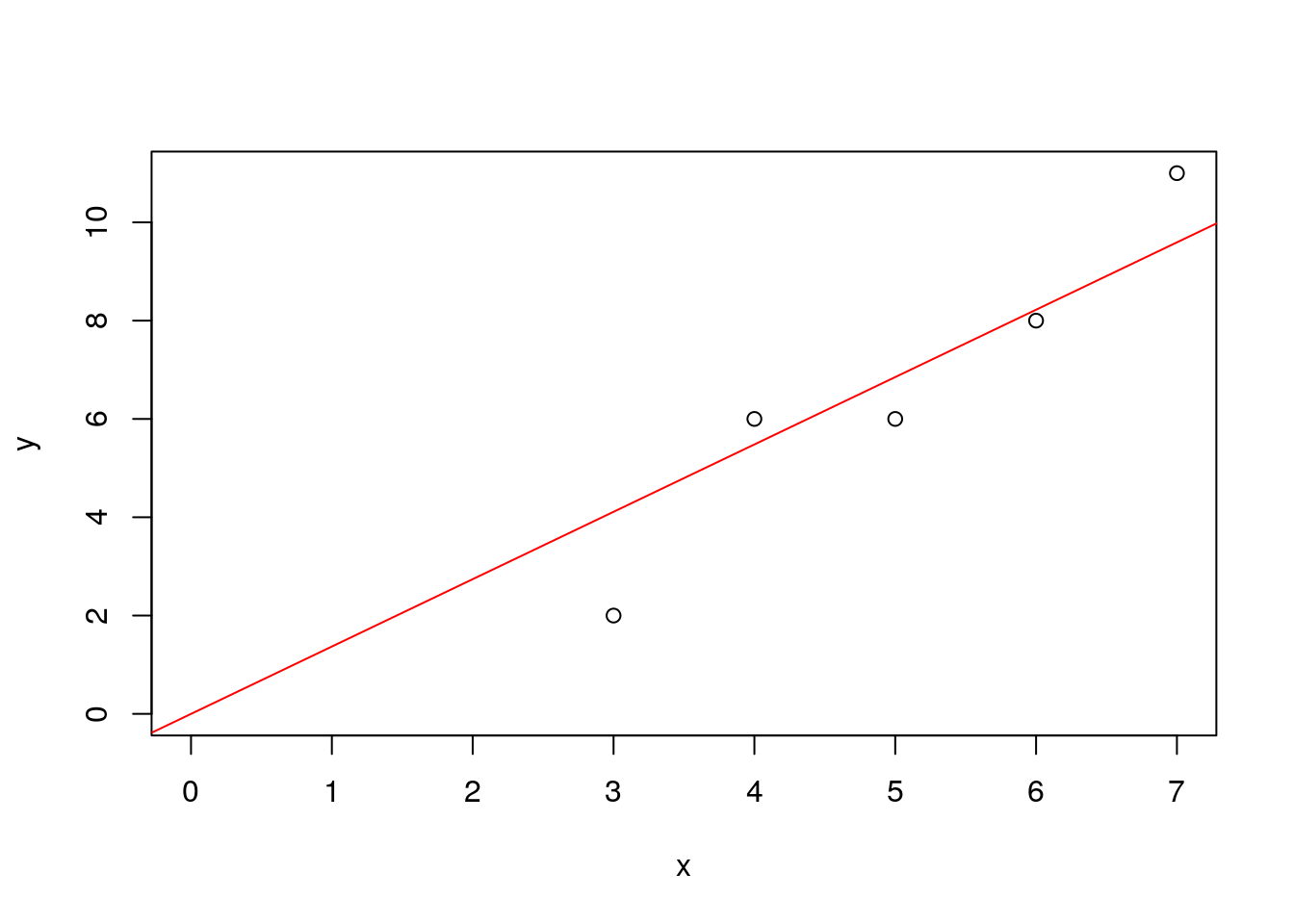

最後に，3次の多項式$ y = _0 + _1,x + _2,x^2 + _3,x^3$ を当てはめる 場合の結果を示す．

X <- cbind(1,x,x^2,x^3) # 計画行列Xを作成(定数項を含む3次多項式)
out <- lsfit(X,y,intercept=F) # 線形モデル y = X b + e を当てはめる  
out$coefficients                       # 回帰係数のみを表示

##                       x                         
## -48.4000000  31.8333333  -6.2500000   0.4166667

yh <- X %*% out$coefficients  # データ点ｘでのｙの推定値
xg <- seq(x[1],x[length(x)],length=51) # 推定多項式の描画点の並び
Xg <- cbind(1,xg,xg^2,xg^3)            # 描画点に基づく計画行列
yhg <- Xg %*% out$coefficients         # 描画点における推定値の並び
plot(x,y)                              # テータ点(x,y)の描画
par(new=T)                             # 追加描画の設定
plot(xg,yhg,type="l",col=2,xlab="",ylab="",axes=F) # 推定多項式の描画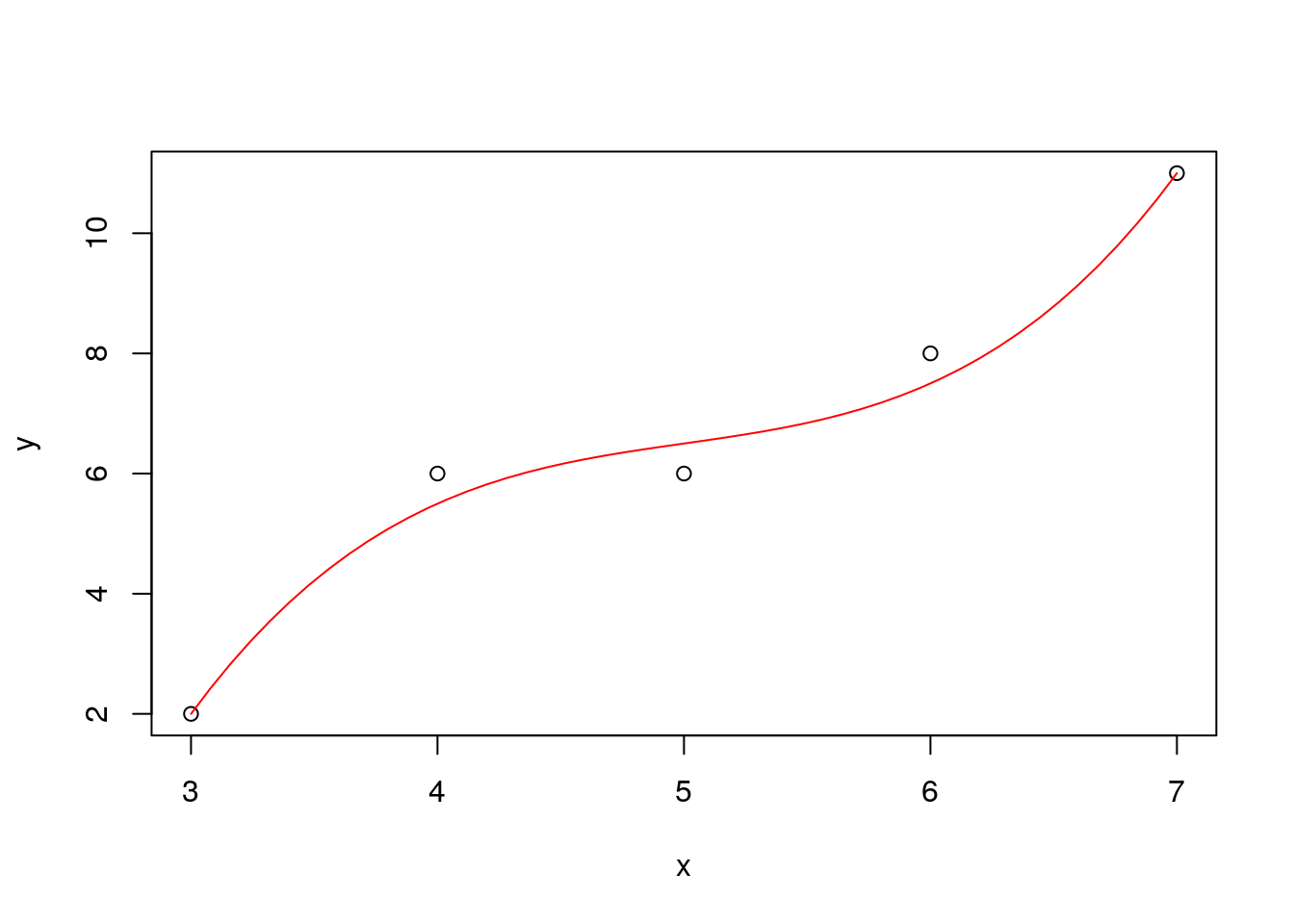

R言語のプログラム環境

プログラム制御

--- program : R-プログラミング -----------------------------------------
* for (i in 1:3) cat(i,"\n")
* if (cond) expr
  if (cond) {expr1; expr2; ...}
  if(cond) cons.expr  else  alt.expr
  if(cond1) expr1            # if else 構文は入れ子にできる
    else if (cond2) expr2
    else expr3
  ifelse(cond, expr1, expr2)  ---> if(cond) expr1 else expr2 
* while(cond) expr    注意：条件 cond は必ず一度は評価される
* repeat と break
   i=0; repeat {if ((i <- i+1) == 5) {cat(i,"\n"); break}} --->   5
* switch
   > centre <- function(x, type) {
       switch(type,
                 mean = mean(x),
                 median = median(x),
                 trimmed = mean(x, trim = .1),
                 "Otherwise"  )   }
   > x <- rcauchy(10); centre(x, "mean")  
  [1] -1.163613  # 文字列 "mean" にマッチした項目の値 mean(x) が返される
* 基本論理演算子
  !x     : x の否定      x == y : 一致             x != y : 不一致   
  x > y  : x が大        x >= y : x が大か等しい   x < y  : x <= y
  x || y : 論理和 (x が TRUE か y が TRUE なら TRUE)
  x && y : 論理積 (x, y が ともに TRUE なら TRUE)
* 関数定義に関して
  func <- function(x,y=NULL,xlim=c(x0,x1),...) { body }
  return(out)
  invisible(list(x=x,y=y))
  [停止] f <- function(x){ifelse(x<=0, stop(message='非負値引数'),log(x))}
  try( func(...) ) <--- エラー回復機能付実行
 ---------------------------------------------------------------------

リストとデータフレーム

--- list : リスト ----------------------------------------------------
 > Lst <- as.list(NA)  # リストオブジェクト Lst の初期化
 > Lst <- list(sex=c(1,2),name=c("Tarou","Hanako"))
 > Lst
 $sex
 [1] 1 2
 $name
 [1] "Tarou"  "Hanako"
 > Lst[[1]]
 [1] 1 2
 > Lst[["sex"]]
 [1] 1 2
 > Lst$sex
 [1] 1 2
 > x=list(vec=1:3, mat=matrix(1:4,c(2,2)),char=c("a","b"))
 > str(x)
 List of 3
  $ vec : int [1:3] 1 2 3
  $ mat : int [1:2, 1:2] 1 2 3 4
  $ char: chr [1:2] "a" "b"

--- df : データフレーム ------------------------------------------------
●  列(i.e. 変数名)ラベルの無いデータファイル
 a  1  2 yes    # 列ラベルの無いデータファイル "temp.data"
 b  2  3  no
 c  5  7 yes
 > x=read.table("temp.data")  # 既定の header=FALSE で読み込み
 > x
   V1 V2 V3  V4    # 列(変数名)ラベルが自動的につけられる
 1  a  1  2 yes
 2  b  2  3  no
 3  c  5  7 yes
●データフレームを直接作る．関数 data.frame()
●  数値ベクトルからデータフレームを作る
 > data.frame(vx=1:3, vy=rnorm(3)) # 3x2のデータフレーム(列ラベル vx,vy)
    vx          vy
 1 1   -0.8481768
 2 2    0.8831475
 3 3    0.2178012
●  数値行列からデータフレームを作る
 > x
      [,1] [,2] [,3]
 [1,]    1    5    9
 [2,]    2    6   10
 [3,]    3    7   11
 [4,]    4    8   12
 > data.frame(x)
   X1 X2 X3
 1  1  5  9
 2  2  6 10
 3  3  7 11
 4  4  8 12
---------------------------------------------------------------------

その他

#　　(R言語はベクトルを意識した言語)
(x <- 1)

## [1] 1

str(x)

##  num 1

(y <- exp(x))

## [1] 2.718282

x <- c(1,2,3); y <- x
for (i in 1:length(x)) { y[i] <- exp(x[i]) }; y  # 従来の発想

## [1]  2.718282  7.389056 20.085537

(y <- exp(x))  # ベクトルx(の各要素)に指数関数を適用する

## [1]  2.718282  7.389056 20.085537

関数の微分

R言語に用意されている関数微分関数D()の使用例を示す．

f <- expression(sin(3*x)); f　　　#　f=sin(x) を表現として定義する

## expression(sin(3 * x))

D(f,"x")　　#　関数fを変数xで微分(数式微分)する

## cos(3 * x) * 3

df <- f　　　#　関数fの3次までの導関数を求める
for (i in 1:3) {
  df <- D(df,"x"); cat("i=",i," : "); print(df)
  }

## i= 1  : cos(3 * x) * 3
## i= 2  : -(sin(3 * x) * 3 * 3)
## i= 3  : -(cos(3 * x) * 3 * 3 * 3)

R言語から数式処理言語Maximaを呼び出す試み

準備: Maxima の使用ライブラリ .maxima/max-init.mac に関数 rfuncout() を作成する 
/****** maximaの数式処理結果をR言語の関数として使用する **************************/
rfuncout(fname,vars,funcbody,[args]) :=
  block(
    system("rm -f tmp-maxima-work"),
    if member(new,args) then system("rm -f tmp-maxima-out"), 
    with_stdout("tmp-maxima-work",
      print(fname," <- function(",vars, "){",
            funcbody, "}")
            ),
    system("cat tmp-maxima-work >> tmp-maxima-out")
    )$
rfuncout_ex() := block([],
   /*** example  ***/
     print("=== rfuncout_ex の使用例 ==="),
     display2d:false,
     define(f(x,y), 2/3*x^2*y), 
     fx : diff(f(x,y),x),
     rfuncout("fxy","x,y",f(x,y),new), /* 新規 */
     rfuncout("fx","x,y",fx),          /* 追記 */
     t5 : taylor(sin(x),x,0,5),
     rfuncout("t","x",t5),             /* 追記 */
     system("cat tmp-maxima-out"),
     return("---end of rfuncout_ex---")
     )$

/*######################################################################*/

#--- R から Maxima を実行するR関数を作成 
rmaxima <- function(maxin){
  system("rm -f tmp-maxima-*")
  sink("tmp-maxima-in"); cat(maxin,"\n");   sink()
  system("max < tmp-maxima-in > out") 
       # maxima ではmaxima-init.macを読まない私的環境に設定されている為
  if (file.exists("tmp-maxima-out"))
    {source("tmp-maxima-out")
     print("File: tmp-maxima-out に出力された内容をR関数として取り込みました．")}
}
#--- Maxima 実行スクリプトの例 (この部分にMaximaプログラムを書く)
maxin <- paste(' \
 display2d:false$ \
 define(f(x,y), 2/3*x^2*y); \
 define(fx(x,y), diff(f(x,y),x))$ \
 t5 : taylor(sin(x),x,0,5); \  /* sin(x) をx=0において5次までTaylor展開する */
 define(t(x), t5)$ \
 /* 結果をRの関数として渡すMaxima私用関数rfuncout()を準備する */ 
 fundef(rfuncout); \   /* 結果が表示できない? */
 rfuncout("f","x,y", f(x,y), new)$ \  /* tmp-maxima-out に新規書き込み */
 rfuncout("fx","x,y", fx(x,y))$ \     /* 追記 */
 rfuncout("t","x",t(x))$ \            /* 追記 */
 quit();\
')
#--- 実行例
rmaxima(maxin)

## [1] "File: tmp-maxima-out に出力された内容をR関数として取り込みました．"

system("cat out")             #　非表示?
system("cat tmp-maxima-out")　　#　非表示?
f; f(2,1)

## function (x, y) 
## {
##     (2 * x^2 * y)/3
## }

## [1] 2.666667

fx; fx(2,1)

## function (x, y) 
## {
##     (4 * x * y)/3
## }

## [1] 2.666667

t # taylor(sin(x),x,0,5) をMaximaにより数式処理した結果をRの関数として受け取る

## function (x) 
## {
##     x - x^3/6 + x^5/120
## }

t(pi/10); sin(pi/10)

## [1] 0.3090171

## [1] 0.309017

curve(sin,xlim=c(-pi,pi),col="blue",lty=2,main="Taylor Expansion of sin(x)")
curve(t,xlim=c(-pi,pi),col="red",lty=1,add=T); abline(h=0); abline(v=0)
legend(1,-0.5,c("sin(x)","Taylor"),col=c("blue","red"),lty=c(2,1))

表のTeX表示

library(xtable)
tab <- matrix(1:6,2,3,byrow=T)
rownames(tab) <- c("row-1","row-2")
colnames(tab) <- c("col-1","col-2","col-3")
print(xtable(tab,digits=4,caption='tab1'))

## % latex table generated in R 3.4.4 by xtable 1.8-2 package
## % Mon Apr 13 07:00:52 2020
## \begin{table}[ht]
## \centering
## \begin{tabular}{rrrr}
##   \hline
##  & col-1 & col-2 & col-3 \\ 
##   \hline
## row-1 &     1 &     2 &     3 \\ 
##   row-2 &     4 &     5 &     6 \\ 
##    \hline
## \end{tabular}
## \caption{tab1} 
## \end{table}

---

統計の基礎

データの記法 (p.6)

[データの記法]

\(n\)個のデータ : \(x_1, \cdots, x_s, \cdots, x_n \quad\) (\(n\) : 標本数，標本の大きさ, データ数)

• 1変量データ > \(\{x_s ;~ s = 1, 2, \cdots, n\}\)
• 2変量データ > \(\{(x_s,~ y_s) ;~ s = 1, 2, \cdots, n\}\)
• p変量データ > \(\{{\bf x}_s = (x_{s1}, \cdots, x_{sj}, \cdots, x_{sp} ) ;~ s = 1, 2, \cdots, n\}\)
  

注 : 本書では個体番号(標本番号)を示す添字を\(s\)で表す．
\(x_s\)は変量\(x\)に関する \(s\) 番目の個体の値を表し，
\(x_{sj}\) は\(s\)番目の個体の第\(j\)変量の値を表す．

基本統計量(1）(p.6)

• データ ： \(\{ x_s; \, s = 1, 2, \, \cdots, n\}\)
• 平均 ： \(\bar{x} = \displaystyle \frac{1}{n} \, \sum_{s=1}^{n} x_s\)
• 分散 ： \(s^2 = \displaystyle \frac{1}{n} \, \sum_{s=1}^{n} \left(x_s - \bar{x} \right)^2\)
• 標準偏差 ： \(s = \sqrt{s^2}\) 分散の平方根

上記は「データから」求める基本統計量の定義式である．
後に，「度数分布表から」求める基本統計量の定義式を示す．
両者を区別して対応できるように．

例1 平均と分散の計算（データより）(p.7)}

例1．データ: 30, 40, 50, 40 (n = 4) について平均，分散，標準偏差を求める． \[\begin{eqnarray*} \bar{x} &=& \frac{1}{n} \sum_{s=1}^{n} x_s = \frac{1}{4} (30 + 40 + 50 + 40) = 40 \\ s^2 &=& \frac{1}{n} \sum_{s=1}^{n}(x_s-\bar{x})^2 \\ &=& \frac{1}{4} \{(30-40)^2 + (40-40)^2 + (50-40)^2 + (40-40)^2\} = 50 \\ s &=& \sqrt{s^2} = \sqrt{50} \doteq 7.07 \end{eqnarray*}\]

                              x
                         x    x    x
          +----+----+----+----+----+----+----+----+---> x
          0   10   20   30   40   50   60   70   80
                         <----*---->

例2 平均と分散の計算（データより）(p.7)}

例1．データ: 30, 40, 50, 40 (n = 4) について:~~\(\bar{x}=40,~ s^2=50,~ s \doteq 7.07\)

                              x
                         x    x    x
          +----+----+----+----+----+----+----+----+---> x
          0   10   20   30   40   50   60   70   80
                         <----*---->

例2．データ: 10, 40, 70, 40 (n = 4) について平均，分散，標準偏差を求める． \[\begin{eqnarray*} \bar{x} &=& \frac{1}{4} (10 + 40 + 70 + 40) = 40 \\[1ex] s^2 &=& \frac{1}{4} \{(10-40)^2 + (40-40)^2 + (70-40)^2 + (40-40)^2\} = 1800/4 = 450 \quad (例1の9倍) \\[1ex] s &=& \sqrt{s^2} = \sqrt{450} \doteq 21.21 \quad \longleftarrow s \doteq 7.07 \end{eqnarray*}\]

                              x
               x              x              x
          +----+----+----+----+----+----+----+----+---> x
          0   10   20   30   40   50   60   70   80
               <--------------*-------------->            

度数分布表へ (p.8)}

例3．データ: 30, 50, 40, 40, 30, 40, 40, 50 (n = 8) について \[\begin{eqnarray*} &\bar{x} &= \dfrac{1}{8} \left(30 + 50 + 40 + 40 + 30 + 40 + 40 + 50\right) \\[1ex] & &= 30 \times 2/8 + 40 \times 4/8 + 50 \times 2/8 \\[1ex] & &= 30 \times 0.25 + 40 \times 0.5 + 50 \times 0.25 \\[1ex] & &= x_1 \times p_1 + x_2 \times p_2 + x_3 \times p_3 \\[1ex] & &= 40 \quad (データ値とその値が全体に占める割合から平均を求めている)\\[2ex] & s^2 &= \frac{1}{8} \Big\{ (30-40)^2 + (50-40)^2 + (40-40)^2 + (40-40)^2 \\[1ex] & & \quad \quad + (30-40)^2 + (40-40)^2 + (40-40)^2 + (50-40)^2 \Big\} \\[1ex] & &= (30-40)^2\times0.25 + (40-40)^2\times0.5 + (50-40)^2\times0.25 \\[1ex] & &= (x_1 - \bar{x})^2 \times p_1 + (x_2 - \bar{x})^2 \times p_2 + (x_3 - \bar{x})^2 \times p_3 \\[1ex] & &= 50 \end{eqnarray*}\]

作業表 \[ \begin{array}{r|c|c|c} \hline i & x_i & f_i & p_i = f_i/n \\ \hline 1 & 30 & 2 & 0.25 \\ 2 & 40 & 4 & 0.50 \\ k=3 & 50 & 2 & 0.25 \\ \hline \end{array}\]

\[\begin{eqnarray*} \bar{x} &=& x_1 \times p_1 + x_2 \times p_2 + x_3 \times p_3 \\[1ex] &=& 30 \times 0.25 + 40 \times 0.5 + 50 \times 0.25 = 40\\[1ex] s^2 &=& (x_1 - \bar{x})^2 \times p_1 + (x_2 - \bar{x})^2 \times p_2 + (x_3 - \bar{x})^2 \times p_3 \\[1ex] &=& (30-40)^2\times0.25 + (40-40)^2\times0.5 + (50-40)^2\times0.25 = 50 \\[1ex] \end{eqnarray*}\]

上記の作業表を一般化したものが度数分布表である．

度数分布表 (p.9)

度数分布表

\[ \begin{array}{c|c|c|c|c|l} \hline 階級番号 & 階級 & 階級値 & 度数 & 相対度数 & 累積相対度数 \\ \hline 1 & [x_{(1)},~~~ x_{(2)}) & x_1 & f_1 & p_1 & F_1 = p_1\\ \vdots & \vdots & \vdots & \vdots & \vdots & \quad \vdots \\ i & [x_{(i)},~ x_{(i+1)}) & x_i & f_i & p_i & F_i = \displaystyle \sum_{j=1}^i p_j\\ \vdots & \vdots & \vdots & \vdots & \vdots & \quad \vdots \\ k & [x_{(k)},~ x_{(k+1)}) & x_k & f_k & p_k & F_k = 1\\ \hline %\multicol{6}{l}{x_{(i)},~x_{(i+1)} をそれぞれ第i階級の左境界値，右境界値という．} %\\ %\mcol{6}{l}{階級} [x_{(i)},~x_{(i+1)}) は x_{(i)} \le x < x_{(i+1)} を表す． }\\ \end{array}\]

\(x_{(i)},~ x_{(i+1)}\) をそれぞれ第 \(i\) 階級の左境界値，右境界値という．
階級 \([x_{(i)}, ~x_{(i+1)})\) は \(x_{(i)} \le x < x_{(i+1)}\) を表す．

平均と分散の定義

\[ \begin{array}{l||l|l} \hline 基本統計量 & データより & 度数分布表より \\ \hline 平均 & \displaystyle \bar{x} = \frac{1}{n} \sum_{s=1}^{n} x_s & \displaystyle \bar{x} = \sum_{i=1}^{k} x_i ~ p_i \\ \hline 分散 & \displaystyle s^2 = \frac{1}{n} \sum_{s=1}^{n}(x_s-\bar{x})^2 & \displaystyle s^2 = \sum_{i=1}^{k}(x_i - \bar{x})^2 ~ p_i \\ \hline \end{array} \]

度数分布表の例 (p.10)

例4．データ : 27, 23, 36, 46, 70, 30, 37, 50, 41, 53 (n = 10) について平均，\ 分散，標準偏差を求める．また，度数分布表を作成し，種々の統計値を求める．

度数分布表

\[ \begin{array}{r|c|c|c|c|c} \hline 階級No & 階級 & 階級値 & 度数 & 相対度数 & 累積相対度数 \\ i & x_{(i)} \sim x_{(i+1)} & x_i & f_i & p_i = f_i/n & F_i = \displaystyle \sum_{j=1}^{i} p_j \cr \hline 1 & 15 \sim 25 & 20 & 1 & 0.1 & 0.1 \cr 2 & 25 \sim 35 & 30 & 2 & 0.2 & 0.3 \cr 3 & 35 \sim 45 & 40 & 3 & 0.3 & 0.6 \cr 4 & 45 \sim 55 & 50 & 3 & 0.3 & 0.9 \cr k=5 & 55 \sim 85 & 70 & 1 & 0.1 & 1.0 \cr \hline %\mcol{6}{l}{階級 $x_{(i)} \sim x_{(i+1)}$ は $x_{(i)} \le x < x_{(i+1)}$ を表す．}\cr \end{array} \]
階級 \(x_{(i)} \sim x_{(i+1)}\) は \(x_{(i)} \le x < x_{(i+1)}\) を表す．

\[ \begin{array}{lll} & [データより] & [度数分布表より] \cr 平均 & \displaystyle \bar{x} = \frac{1}{n} \sum_{s=1}^n x_s = 41.3 & \displaystyle \bar{x} = \sum_{i=1}^k x_i ~ p_i = 42 \cr 分散 & \displaystyle s^2 = \frac{1}{n} \sum_{s=1}^n (x_s - \bar{x})^2 = 177.21 & \displaystyle s^2 = \sum_{i=1}^k (x_i - \bar{x})^2 ~ p_i = 176 \cr 標準偏差 & \displaystyle s = \sqrt{s^2} = 13.31 & \displaystyle s = \sqrt{s^2} = 13.27 \cr \end{array} \] 注： 度数分布表より求めた基本統計量の値(例えば平均 \(\bar{x}\) の値)は データから求めた値と異なる．
データ値 23 は 第1階級に入るが，このデータを第1階級の階級(代表)値 20 に置き換えている．

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
### ヒストグラムと経験分布関数のグラフ (p.11)
\fs{8}{9}
\vspace*{-0.5cm}
\FIGCAP{\includegraphics[width=8cm,height=6cm]{/home/inoue/Stat14/Fund/D1C-out.pdf}}
       {ヒストグラム(上図)と経験分布関数(累積相対度数)グラフ(下図)}
\vspace{-5ex}
\fs{9}{10}
\begin{enumerate}
\item[注1]{}
ヒストグラムにおいて，柱の面積が各階級の相対度数に対応する．したがって，
縦軸は\Color{Red}{「相対度数の密度」}を表わす．
\item[注2]{}
累積相対度数のグラフにおいて，点 {(15, 0), (25, 0.1), ... ,(85, 1.0)}
を線分で結ぶと $x$ の関数 $F(x)$ を得る．この関数を
\Color{Red}{経験分布関数}という．
\item[注3]{}
累積相対度数のグラフより，「35以下(未満)のデータは全体の30\%を占める」
と言える．これを，
データの\Color{Red}{「30\%点(パーセント点)は35である」}という．
\end{enumerate}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

25%点の求め方 (p.12)

           累積相対度数のグラフ(経験分布関数のグラフ)--->パーセント点
     y =  F(x)    
     1.0 |- - - - - - - - - - - - - - - - - - - -*
     0.9 |- - - - - - - - - - - - *              :        
     0.8 |                        :              :    
     0.7 |                        :              :       
     0.6 |- - - - - - - - - -*    :              :      
     0.5 |                   :    :              :        
     0.4 |                   :    :              :      
     0.3 |- - - - - - - *    :    : 横軸の値は階級境界値(階級値ではない)
     0.2 |              :    :    :              :     
     0.1 |- - - - -*    :    :    :              :          
     0   +----*----+----+----+----+----+----+----+--> x
         5   15   25   35   45   55   65   75   85   
                   <----> 第2階級

\[ x_{0.25} = 25 + (35 - 25) \times \dfrac{0.25 - 0.1}{0.3 - 0.1} = 32.5 \]

主なパーセント点 (p.12)

\[ \begin{array}{l} 25\%点(第1四分位数:Q_1) \\ \qquad \displaystyle x_{0.25} = 25 + (35-25) \times \frac{0.25-0.1}{0.3-0.1} = 25 + 7.5 = 32.5 \\ 50\%点(中央値) \\ \qquad \displaystyle x_{0.50} = 35 + (45-35) \times \frac{0.50-0.3}{0.6-0.3} = 35 + 6.66 = 41.66 \\ 75\%点(第3四分位数:Q_3) \\ \qquad \displaystyle x_{0.75} = 45 + (55-45) \times \frac{0.75-0.6}{0.9-0.6} = 45 + 5 = 50 \\ 四分位範囲 \\ \qquad R = Q_3 - Q_1 = x_{0.75} - x_{0.25} = 50 - 32.5 = 17.5 \end{array} \] パーセント点はよく用いられる統計値である．\ 80%点，90%点，95%点，98%点，99%点，99.5%点，．．．

２変量データの記述(共分散と相関係数) (p.16)

2変量データ： \(\{(x_s, y_s) ;~ s = 1, \cdots, n\}\)
\[ 共分散：~~ s_{xy} = \dfrac{1}{n} \sum_{s=1}^{n} (x_s - \bar{x})(y_s - \bar{y}) \hspace{1em} 相関係数：~~ r_{xy} = \dfrac{s_{xy}}{s_{x}\cdot s_{y}} \]

ここで，各データ \((x_s,\,y_s)\) 毎の \((x_s - \bar{x})(y_s - \bar{y})\) の符号に着目する． \[ 標準化変換 : ~ z_x(x_s) = \frac{(x_s - \bar{x})}{s_x} \qquad z_y(y_s) = \frac{(y_s - \bar{y})}{s_y} \] \[ r_{xy} = \frac{s_{xy}}{s_x \cdot s_y} = \frac{1}{n} \sum_{s=1}^{n} \frac{(x_s - \bar{x})}{s_x} \cdot \frac{(y_s - \bar{y})}{s_y} \] 相関係数\(r_{xy}\)は単位を持たない係数となることが判る．

標準化散布図と相関係数 (p.17)

\centerline{\includegraphics[width=8cm,height=6cm]{cor-scatter.pdf} }
\clearpage

２変量データの記述 (p.18)

2変量度数分布表の形式 \[ \begin{array}{c|c|c||ccccc||c} \hline & & & 1 & & j & & \ell & \\ & & & y_{(1)}\sim y_{(2)} & \cdots & y_{(j)}\sim y_{(j+1)} & \cdots & y_{(\ell)}\sim y_{(\ell+1)} & p_{i\cdot}\\ & & & y_1 & \cdots & y_j & \cdots & y_\ell & \\ \hline \hline 1 & x_{(1)}~\sim ~x_{(2)} & x_1 & p_{11} & \cdots & p_{1j} & \cdots & p_{1\ell} & p_{1\cdot} \\ \vdots & \vdots & \vdots & \vdots & & \vdots & & \vdots & \vdots \\ i & x_{(i)} \sim x_{(i+1)} & x_i & p_{i1} & \cdots & p_{ij} & \cdots & p_{i\ell} & p_{i\cdot} \\ \vdots & \vdots & \vdots & \vdots & & \vdots & & \vdots & \vdots \\ k & x_{(k)} \sim x_{(k+1)} & x_k & p_{k1} & \cdots & p_{kj} & \cdots & p_{k\ell} & p_{k\cdot} \\ \hline \hline & p_{\cdot j} & & p_{\cdot 1} & \cdots & p_{\cdot j} & \cdots & p_{\cdot \ell} & p_{\cdot\cdot} \\ \hline \end{array} \]

\[ \begin{array}{llp{10cm}} p_{ij} & 同時(結合)相対度数 & xに関して第i階級かつ y に関して第j階級に属する標本の全標本数に対する相対度数\\ p_{i\cdot} & xの周辺相対度数 & $= \displaystyle \sum_{j=1}^{\ell} p_{ij}$ \\ p_{\cdot j} & yの周辺相対度数 & $= \displaystyle \sum_{i=1}^{k} p_{ij}$ \\ \end{array} \]

基本統計量(2) (p.18)

\[ \begin{array}{l|l|l} \hline 基本統計量 & データより & 度数分布表より \\ \hline xの平均 & \displaystyle \bar{x} = \frac{1}{n} \sum_{s=1}^n x_s & \displaystyle \bar{x} = \sum_{i=1}^k x_i \cdot p_{i\cdot} \\ xの分散 & \displaystyle s_x^2 = s_{xx} = \frac{1}{n} \sum_{s=1}^n (x_s - \bar{x})^2 & \displaystyle s_x^2 = s_{xx} = \sum_{i=1}^k (x_i - \bar{x})^2 \cdot p_{i\cdot} \\ yの平均 & \displaystyle \bar{y} = \frac{1}{n} \sum_{s=1}^n y_s & \displaystyle \bar{y} = \sum_{j=1}^\ell y_j \cdot p_{\cdot j} \\ yの分散 & \displaystyle s_y^2 = s_{yy} = \frac{1}{n} \sum_{s=1}^n (y_s - \bar{y})^2 & \displaystyle s_y^2 = s_{yy} = \sum_{j=1}^\ell (y_j - \bar{y})^2 \cdot p_{\cdot j} \\ xとyの{\bf 共分散} & \displaystyle s_{xy} = \frac{1}{n} \sum_{s=1}^n (x_s - \bar{x})(y_s - \bar{y}) & \displaystyle s_{xy} = \sum_{i=1}^k \sum_{j=1}^\ell (x_i - \bar{x}) (y_j - \bar{y}) \cdot p_{ij} \\ xとyの{\bf 相関係数} & \displaystyle r_{xy} = \frac{s_{xy}}{s_x \cdot s_y} & \displaystyle r_{xy} = \frac{s_{xy}}{s_x \cdot s_y} \\ \hline \end{array} \]

注： \(x\) と \(y\) の共分散 \(s_{xy}\) の式(データより)を用いて，\(x\) と \(x\) の共分散 \(s_{xx}\) を考えると \(x\) の分散 \(s_x^2\) を得る．これより，\(x\) の分散 \(s_x^2\) を \(s_{xx}\) で 表わすことがある．

[例5] ２変量データの記述 (p.19)

\[\begin{array}{c|ccccccccccl} \hline s & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 &= n \\ \hline x_s & 27 & 23 & 36 & 46 & 70 & 30 & 37 & 50 & 41 & 53 \\ y_s & 0 & 0 & 2 & 3 & 2 & 1 & 1 & 2 & 3 & 5 \\ \hline \end{array}\]

２変量度数分布表

\[ \begin{array}{rcc||ccccc||c} \hline & & & j: & 1 & 2 & 3 & 4 =l& \\ & & & y: & -0.5\sim0.5 & 0.5\sim1.5 & 1.5\sim2.5 & 2.5\sim5.5 & \\ i & x & x_i& y_j: & 0 & 1 & 2 & 4 & x: p_{i\cdot} \\ \hline \hline 1 & 15\sim25 & 20 & & 0.1 & & & & 0.1 \\ 2 & 25\sim35 & 30 & & 0.1 & 0.1 & & & 0.2 \\ 3 & 35\sim45 & 40 & & & 0.1 & 0.1 & 0.1 & 0.3 \\ 4 & 45\sim55 & 50 & & & & 0.1 & 0.2 & 0.3 \\ k= 5 & 55\sim85 & 70 & & & & 0.1 & & 0.1 \\ \hline \hline & y: p_{\cdot j} && & 0.2 & 0.2 & 0.3 & 0.3 & 1.0 \\ \hline \end{array} \]

\[ xの平均 : \bar{x} = \sum_{i=1}^{5} x_i \cdot p_{i\cdot} = 42, \quad yの平均 : \bar{y} = \sum_{j=1}^4 y_j \cdot p_{\cdot j} = 2.0 \]

２変量度数分布表より共分散を求める (p.20)

◎ メモ : 記法

\(\displaystyle \sum_{i=1}^{k} \sum_{j=1}^{\ell} a_{ij} = \sum_{i=1}^{k} \left\{ \sum_{j=1}^{\ell} a_{ij} \right\}\) について

\[\begin{array}{ccl} \displaystyle \sum_{i=1}^{k} \sum_{j=1}^{\ell} a_{ij} &=& \displaystyle \sum_{j=1}^{\ell} a_{1j} + \sum_{j=1}^{\ell} a_{2j} + \cdots + \sum_{j=1}^{\ell} a_{kj} \\ &=& a_{11} + a_{12} + \cdots + a_{1\ell} \qquad (i=1 のとき) \\ &~~~~~+& a_{21} + a_{22} + \cdots + a_{2\ell} \qquad (i=2 のとき)\\ && \quad \cdots \cdots \\ &~~~~~+& a_{k1} + a_{k2} + \cdots + a_{k\ell} \qquad (i=k のとき) \\ \end{array}\]

\(a_{ij}\) として \((x_i - \bar{x})(y_j - \bar{y}) \cdot p_{ij}\) を考えると 次式を得る．

\[ \begin{array}{ccl} \displaystyle s_{xy} &=& \displaystyle \sum_{i=1}^k \sum_{j=1}^{\ell} (x_i - \bar{x})(y_j - \bar{y}) \cdot p_{ij}\\ &=& \displaystyle \sum_{i=1}^k \left\{ \sum_{j=1}^{\ell} (x_i - \bar{x})(y_j - \bar{y}) \cdot p_{ij} \right\} \\ &=& \displaystyle \sum_{i=1}^k \left\{ (x_i - \bar{x}) \sum_{j=1}^{\ell} (y_j - \bar{y}) \cdot p_{ij} \right\} \\ % &=& (x_1-\bar{x})(y_1-\bar{y})p_{11} + (x_1-\bar{x})(y_2-\bar{y})p_{12} % + \cdots + (x_1-\bar{x})(y_{\ell}-\bar{y})p_{1\ell}\\ % &~~~~~~+& % (x_2-\bar{x})(y_1-\bar{y})p_{21} + (x_2-\bar{x})(y_2-\bar{y})p_{22} % + \cdots + (x_2-\bar{x})(y_{\ell}-\bar{y})p_{2\ell}\\[-1ex] % && \qquad \cdots \cdots \\[-1ex] % &~~~~~~+& % (x_k-\bar{x})(y_1-\bar{y})p_{k1} + (x_k-\bar{x})(y_2-\bar{y})p_{k2} % + \cdots + (x_k-\bar{x})(y_{\ell}-\bar{y})p_{k\ell}\\ &=& (x_1-\bar{x})\Big\{ (y_1-\bar{y})p_{11} + (y_2-\bar{y})p_{12} + \cdots + (y_{\ell}-\bar{y})p_{1\ell} \Big\} \\[-1ex] &~~~~~~+& (x_2-\bar{x})\Big\{ (y_1-\bar{y})p_{21} + (y_2-\bar{y})p_{22} + \cdots + (y_{\ell}-\bar{y})p_{2\ell} \Big\} \\[-1ex] && \qquad \cdots \cdots \\[-1ex] &~~~~~~+& (x_k-\bar{x})\Big\{ (y_1-\bar{y})p_{k1} + (y_2-\bar{y})p_{k2} + \cdots + (y_{\ell}-\bar{y})p_{k\ell} \Big\} \end{array} \]

[例5] ２変量データの記述(共分散を求める) (p.20)

２変量度数分布表

\[ \begin{array}{rcc||ccccc||c} \hline & & & j: & 1 & 2 & 3 & 4 =l& \\ & & & y: & -0.5\sim0.5 & 0.5\sim1.5 & 1.5\sim2.5 & 2.5\sim5.5 & \\ i & x & x_i& y_j: & 0 & 1 & 2 & 4 & x: p_{i\cdot} \\ \hline \hline 1 & 15\sim25 & 20 & & 0.1 & & & & 0.1 \\ 2 & 25\sim35 & 30 & & 0.1 & 0.1 & & & 0.2 \\ 3 & 35\sim45 & 40 & & & 0.1 & 0.1 & 0.1 & 0.3 \\ 4 & 45\sim55 & 50 & & & & 0.1 & 0.2 & 0.3 \\ k= 5 & 55\sim85 & 70 & & & & 0.1 & & 0.1 \\ \hline \hline & y: p_{\cdot j} && & 0.2 & 0.2 & 0.3 & 0.3 & 1.0 \\ \hline \end{array} \]

\[ xの平均 : \bar{x} = \sum_{i=1}^{5} x_i \cdot p_{i\cdot} = 42, \quad yの平均 : \bar{y} = \sum_{j=1}^4 y_j \cdot p_{\cdot j} = 2.0 \]

\[ \begin{array}{rll} & 共分散 ： s_{xy} &= \displaystyle \sum_{i=1}^5 \sum_{j=1}^4 (x_i - \bar{x}) (y_j - \bar{y}) \cdot p_{ij} \\ & &= (20 - 42)(0 - 2)\cdot 0.1 \\ & &\quad + (30 - 42) \Big\{ (0 - 2)\cdot 0.1 + (1 - 2)\cdot 0.1 \Big\}\\ & &\quad + (40 - 42) \Big\{ (1 - 2)\cdot 0.1 + (2 - 2)\cdot 0.1 + (4 - 2)\cdot 0.1 \Big\} \\ & &\quad + (50 - 42) \Big\{(2 - 2)\cdot 0.1 + (4 - 2)\cdot 0.2 \Big\}\\ & &\quad + (70 - 42) \Big\{(2 - 2)\cdot 0.1 \Big\}\\ & &= 11 \end{array} \]

相関係数(省略)

相関係数\(r_{xy}\)について \[ \begin{array}{rll} & r_{xy} &= \displaystyle \frac{s_{xy}}{s_x \cdot s_y} \\ & &= \displaystyle \frac{1}{n} \sum_{s=1}^{n} \frac{(x_s - \bar{x})}{s_x} \cdot \frac{(y_s - \bar{y})}{s_y} \qquad \leftarrow s_{xy} = \frac{1}{n} \sum_{s=1}^{n} (x_s - \bar{x})(y_s - \bar{y}) \\ & &= \displaystyle \frac{1}{n} \sum_{s=1}^{n} z_x(x_s) \cdot z_y(y_s) \\ \end{array} \]

\[ 標準化変換 : z_x(x_s) = \frac{(x_s - \bar{x})}{s_x} \qquad z_y(y_s) = \frac{(y_s - \bar{y})}{s_y} \]

                               
                                  散布図
           y                                      y                 
                     |     *                                |          
       |   |         |  * *                   |   |  *  *   |        
       |   |         | ** *                   |   |     * * |             
       |   |       * * ***                    |   |      **** *          
       *   |--------*+**-**----->             *   | ----**-*+***-**-----> 
       |   |     *  *** *                     |   |        *** *          
       |   |    **** * *                      |   |         |** **        
       |   |   ** *  |                        |   |         |  *  *     
           |   *     |                            |         |    *        
     ------------------------>x              ------------------------>x    
           |    <----*---->                       |    <----*---->    

               r_xy ≒ 0.7                            r_xy ≒ -0.7

相関係数の性質

• 相関係数は，2つの変量\(x\)，\(y\)の間の線形傾向(直線傾向)の強さを示す指標
• 次の不等式が成り立つ: \(-1 \le r_{xy} \le 1\)

標準化変換と散布図 (p.21)

\[ \hspace{4em}標準化変換 : \quad z_x(x_s) = \frac{x_s - \bar{x}}{s_x} \qquad z_y(y_s) = \frac{y_s - \bar{y}}{s_y} \]

2.4 多変量のデータの記述 (p.22)

\(p\)変量データ： \(\{(x_{s1}, \cdots, x_{sj}, \cdots, x_{sp}) ; ~s = 1, \cdots, n\}\) _~ \(x_{sj}\) : \(s\)番目の個体の第\(j\)変量の値を表す．

データ行列： \(X = \begin{pmatrix} x_{11} & ... & x_{1j} & ... & x_{1p} \cr \vdots & & \vdots & & \vdots \cr x_{s1} & ... & x_{sj} & ... & x_{sp} \cr \vdots & & \vdots & & \vdots \cr x_{n1} & ... & x_{nj} & ... & x_{np} \end{pmatrix}\)

1. 第\(j\)変量の平均 : \(\bar{x}_{j} = \displaystyle \frac{1}{n} \sum_{s=1}^{n} x_{sj}\) \(\Longrightarrow\) 平均ベクトル： \(\bar{x} = (\bar{x}_1, \cdots, \bar{x}_j, \cdots, \bar{x}_p)\)
   
2. 第\(i\)変量と第\(j\)変量との共分散 : \(\displaystyle s_{ij} = \frac{1}{n} \sum_{s=1}^{n} (x_{si} - \bar{x}_i)(x_{sj} - \bar{x}_j)\) \(\Longrightarrow\) 分散・共分散行列：\(S\)
   
3. 第\(i\)変量と第\(j\)変量との相関係数 : \(\displaystyle r_{ij} = \frac{s_{ij}} {\sqrt{s_{ii}} \cdot \sqrt{s_{jj}}}\) \(\Longrightarrow\) 相関行列：\(R\\[1ex]\)
   \(S = \begin{pmatrix} s_{11} & ... & s_{1j} & ... & s_{1p} \cr \vdots & & \vdots & & \vdots \cr s_{i1} & ... & s_{ij} & ... & s_{ip} \cr \vdots & & \vdots & & \vdots \cr s_{p1} & ... & s_{pj} & ... & s_{pp} \end{pmatrix}\) \(\quad ,\) \(R = \begin{pmatrix} r_{11} & ... & r_{1j} & ... & r_{1p} \cr \vdots & & \vdots & & \vdots \cr r_{i1} & ... & r_{ij} & ... & r_{ip} \cr \vdots & & \vdots & & \vdots \cr r_{p1} & ... & r_{pj} & ... & r_{pp} \end{pmatrix}\)

上記 1，2，3 を多変量データの基本統計量という．

多変量データの解析例 (p.23)

◎サイズ40の4変量データ  (p = 4,  n = 40)

    No. 英語 数学 国語 社会           No. 英語 数学 国語 社会
     1   50   62   54   52           21   39   32   68   69
     2   36   30   56   53           22   44   39   59   64
     3   48   44   59   74           23   54   38   69   76
     4   50   28   53   63           24   72   72   52   71
     5   40   43   66   77           25   45   48   64   70
     6   46   40   51   65           26   50   61   54   53
     7   45   28   75   74           27   56   55   67   72
     8   76   78   70   89           28   39   38   49   67
     9   62   68   58   57           29   39   53   49   48
    10   43   48   69   75           30   38   30   63   69
    11   47   48   50   63           31   60   57   68   69
    12   44   33   57   58           32   42   40   50   51
    13   53   75   43   56           33   43   41   64   73
    14   39   33   48   75           34   58   47   79   70
    15   69   73   49   45           35   49   51   54   56
    16   56   58   52   48           36   66   72   85   68
    17   57   43   75   65           37   50   64   53   56
    18   58   38   66   75           38   47   65   67   65
    19   43   48   74   79           39   45   48   63   75
    20   56   78   74   63           40   35   35   62   75

多変量データの解析例 (p.23)

◎基本統計量 
                  英語         数学        国語        社会
  　総ケース数   40.0000000  40.0000000 40.0000000  40.0000000
  有効ケース数   40.0000000  40.0000000 40.0000000  40.0000000
  　　　最大値   76.0000000  78.0000000 85.0000000  89.0000000
  　　　最小値   35.0000000  28.0000000 43.0000000  45.0000000
  　　　中央値   47.5000000  48.0000000 60.5000000  67.5000000
  　　２５％点   43.0000000  38.0000000 52.7500000  56.7500000
  　　５０％点   47.5000000  48.0000000 60.5000000  67.5000000
  　　７５％点   56.0000000  61.2500000 68.0000000  74.0000000
  　　不偏分散   99.3326923 223.8948718 98.6641026 101.1737179
  　　標準偏差    9.9665788  14.9631170  9.9329805  10.0585147
  　　算術平均   49.7250000  49.5500000 60.9500000  65.5750000
                     
 分散・共分散行列 
                 英語         数学       国語        社会 
        英語  99.332692  106.8217949 20.0884615    2.905769
        数学 106.821795  223.8948718  0.2589744  -31.862821
        国語  20.088462    0.2589744 98.6641026   58.029487
        社会   2.905769  -31.8628205 58.0294872  101.173718

 相関行列 
                 英語        数学        国語        社会 
        英語 1.00000000  0.716294587 0.202918202  0.02898552
        数学 0.71629459  0.999999940 0.001742429 -0.21170361
        国語 0.20291820  0.001742429 0.999999940  0.58081162
        社会 0.02898552 -0.211703613 0.580811620  1.00000000

source("/home/inoue/r-ex/RLIB")
options(width=60,dights=4)
X0 <- read.csv("/home/inoue/r-ex/dex2.csv")
head(X0,3)

##   No. 英語 数学 国語 社会
## 1   1   50   62   54   52
## 2   2   36   30   56   53
## 3   3   48   44   59   74

par(family="Japan1")
df <- data.frame(X0[,-1])
boxplot(df,main="箱ひげ図(四分位数による)")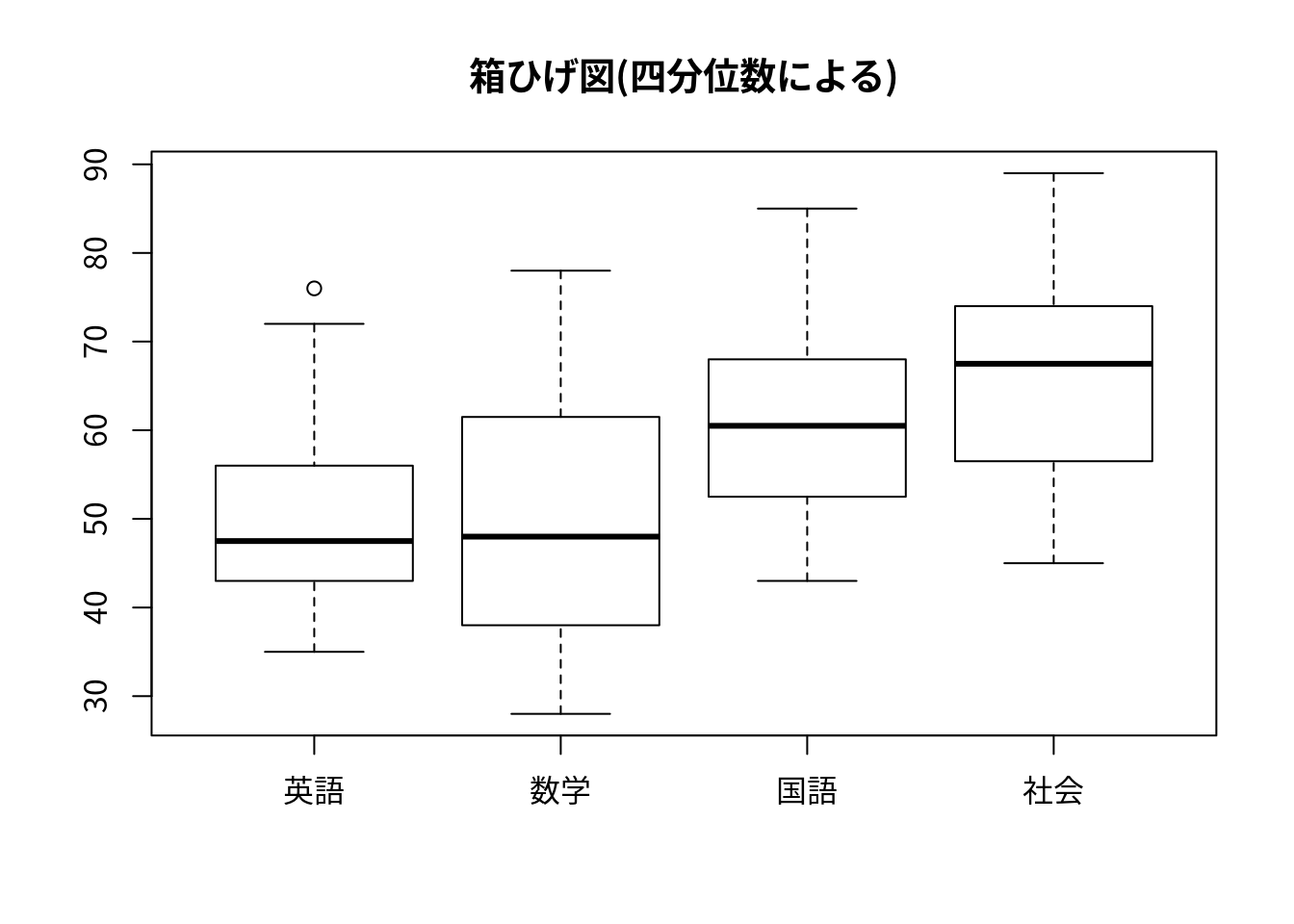

箱ヒゲ図は左から英語，数学，国語，社会を表す．
箱ヒゲ図(右図)について
    黒丸      中央値
    箱の上下    第3四分位数，第1四分位数
    ヒゲの上下   四分位範囲の±1.5倍以内での最大外れ値
    白丸      外れ値

par(family="Japan1")
pairs1(df)

散布図行列の例 (p.24)

標準化後の散布図になっている．また，数字は個体番号を識別している．