多変数不等式の求解への試み
INOUE Takakatsu 2024-05-11
言語エンジンeng_langの環境設定
HOME <- system("echo ${HOME}", intern=T)
setup_file <- paste(HOME,"/bin/eng_lang_setup.R",sep="")
source(setup_file)## === knitr, (reticulate,) eng_lang are go. ===on3env() : on3ライブラリーのロードとlispファイルの書き出し
batchload("/home/inoue/Maxlib-20/on3lib21.mx")$
on3env()$
max_save()$ /* lisp ファイルに書き出す */## ~/bin/go TMP/tmp_lang/chunk-1.mx > TMP/tmp_lang/chunk-1.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-1.mx")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-1.mx
## batchload("/home/inoue/Maxlib-20/on3lib21.mx")
## on3env()
## -- <on3env> logbegin --
## maxima_tempdir = TMP/tmp_maxima figs_dir = figs
## max_save()
## save("/tmp/max_save.lisp", all)
## "/var/www/html/LANG/TMP/tmp_lang/chunk-1.mx"- 注: 20011年に応用統計学に掲載された内容ですが,その後のプログラムがかなり変更されています。本稿では,プログラム変更に伴い,当時の例題が正しく動作するかを確認する目的で RMarkDown を用いて時々検証しています。以下はその結果です。
0 要旨
多変数関数に関する不等式を解く問題を取り上げる.多変数関数としては,多変数多項式とそれを分子,分母にもつ有理式を想定する.また連立不等式の場合を取り上げる.不等式求解の手順を示し,それを,数式処理言語 Maxima 上に関数 on3ineq() として作成する.機能検証のための使用例を示す.
1 はじめに
数式処理言語を用いて,多変数関数 \(f(x,y_1,...,y_m,z)\) に関する不等式 \[ f_l \leq f < f_r \] を,変数 \(x,y_1,...,y_m,z\) について解く問題を考える.
数式処理言語としては,商用でなく,かつ
Windows版,MacOS版,Linux版が用意されている点を考慮して,
Maxima(中川(2002),横田(2006,2007)参照)を用いることとする.
解くべき不等式をMaxima上に関数表現 on3ineq([f,fl,fr,lr])
を用いて定める.ここで,引数f,fl,frは多変数多項式または多変数多項式を分子,分母にもつ有理式とする.
引数lrは開閉を表すシンボル (\(f_l \leq f \leq
f_r\) のときcc, \(f_l \leq f <
f_r\) のときco, \(f_l < f \leq
f_r\) のときoc, \(f_l < f <
f_r\) のときoo)とする.
また,不等式が \(f_l \leq f\)
で現れるときは \(f_l \leq f <
\infty\) と見なしon3ineq([f,fl,inf,co]),\(f < f_r\) で現れるときは \(- \infty < f < f_r\) と見なし
on3ineq([f,minf,fr,oo]) の様に与える. 不等式の解は,3変数 \(x,y,z\)の場合
\[
\sum_{i} on3(x,xl_i,xr_i,xlr_i)*
on3(y,yl_i(x),yr_i(x),ylr_i)*
on3(z,zl_i(x,y),zr_i(x,y),zlr_i)
\] の様に表す.ここで,関数
on3(x,xl,xr,xlr)はx:変数または式,xl:左境界,xr:右境界,xlr:開閉シンボル(cc,co,oc,oo)を用いてxに関する区間を定義・評価する.xlr=coの場合では,\(xl \leq x < xr\) のとき 1(true)
を返し,その他のとき 0(false)
を返す.また,評価不定の場合は定義式を返す(井上(2008)参照).
以下に,2変数不等式
\[
\frac{1}{x-1} \leq \frac{x-y}{(x-1)(y-2)} < \frac{1}{y-2}
\]
を解く例を実行例1に示す.なお,関数on3show()は結果の表示関数(井上(2008)参照)であり,実行例内の
<–は注釈を表す.
実行例 1
(%i2) display2d:false$
(%i3) out:on3ineq([(x-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co]); <-- 不等式の定義
(%o3) on3(x,2,inf,oo)*on3(y,2,(x+2)/2,oc) <-- 不等式の解(on3関数表現)
+on3(x,0,1,oo)*on3(y,1,(x+2)/2,oc)
(%i4) display2d:true$
(%i5) on3show(out)$ <-- 不等式の解(表示関数による)
[ 1 (0 < x < 1) & (1 < y <= (x+2)/2) ]
out = [ 1 (2 < x < inf) & (2 < y <= (x+2)/2) ]
[ 0 ( otherwise ) ] - Maxima 実行例1
display2d:false$
if false then out:on3ineq([(x-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co]); /* <-- 不等式の定義 */
out : on3ineq([(x-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co],'title = "ex1",
'xrange = [-2,6],'yrange = [0,4],
'file_name = "figs/jjas-ex1",'noview,
'resultonly,'outsum);
display2d:true$
on3show(out)$ ## ~/bin/go TMP/tmp_lang/chunk-2.mxl > TMP/tmp_lang/chunk-2.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-2.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-2.mxl
## display2d:false
## if false then out:on3ineq([(x-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co])
## false
## out:on3ineq([(x-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co],'title = "ex1",'xrange = [-2,6],
## 'yrange = [0,4],'file_name = "figs/jjas-ex1",'noview,'resultonly,'outsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## display2d:true
## on3show(out)
## out = out
## /var/www/html/LANG/TMP/tmp_lang/chunk-2.mxl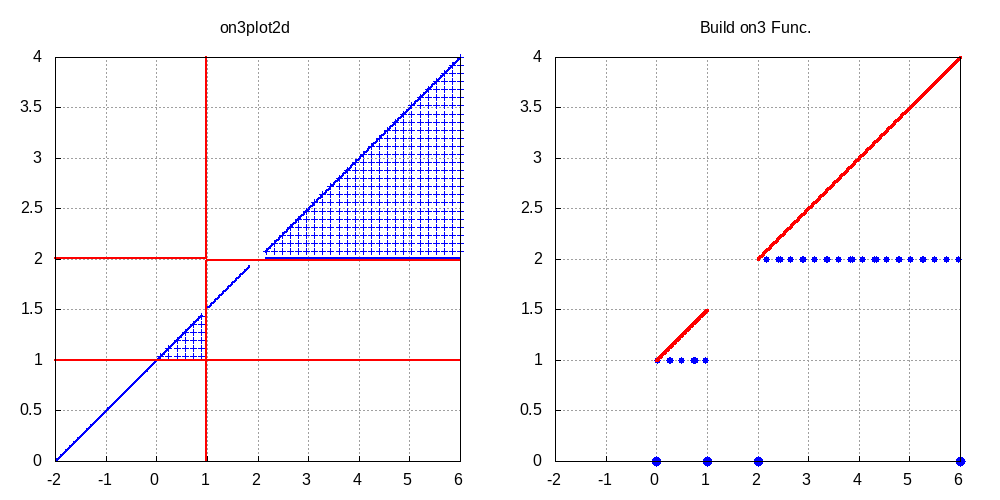
数式処理言語 Maxima では,不等式の求解機能は標準では提供されていないが, maxima/バージョン/share/contrib ディレクトリ内のファイル solve_rat_ineq.mac に1変数多項式とその有理式の不等式を解く 関数 solve_rat_ineq() が提供されている. 本稿の関数 on3ineq() は,上記関数 solve_rat_ineq(). この機能により,不等式によって定まる定義域上での関数の多重積分 等の数式処理に寄与すると考えられる (井上(2008)参照). なお,商用の数式処理言語 Mathematica では,Reduce 関数があり,関連する処理関数との連携もよく整備されている.しかしながら,Mathematica,および,その構成手順を明らかにすることは重要であると考える. 加えて,統計処理言語 R の様な商用でない処理言語の中で数式処理言語を呼び出して用いるような状況では,上記のような機能を商用でないプログラムとして整備しておくことは重要であると考える.
2 解法手順
以下では,多変数関数\(f(x,y_1,...,y_m,z)\) に関する不等式を,記号の煩雑さを避ける意味で3変数関数 \(f(x,y,z)\) の場合について説明する. なお,2変数関数\(f(x,y)\)の場合は,中間変数\(y\)がなく,最終変数\(z\)を改めて\(y\)と見なす.1変数関数\(f(x)\)も同様に見なす. 不等式 \[ f_l \leq f(x,y,z) < f_r \] の解領域の境界は方程式 \(f(x,y,z)-f_l=0\) および \(f(x,y,z)-f_r=0\) で表せ,それらを境界方程式と呼ぶことにし,その一般形を\(F(x,y,z)=0\)で表す. 与不等式の求解には,派生する境界方程式ごとに行う”零点表示処理”(齋藤他(2003),近藤他(2005)参照)と,派生境界方程式から2個の方程式の組合せを作り,それらの組に対して連立方程式を解く”交点処理”を必要とする. 解の表示には,曲面を陽関数表示\((x,\,y=y(x),\,z=z(x,y))\)で表し,孤立点を\((x=x_0,y=y_0,z=z_0)\),孤立線を\((x=x_0,\,y=y,\,z=z(y))\) の様に表す. 陽関数表示では,\((z,\,y=y(z),\,x=x(z,y))\)といった表現が必要になる場合もあり,それらは変数(の消去する)順序と関連する.本稿では変数順序を明示的に指定しない場合は\((x,\,y=y(x),\,z=z(x,y))\)を用い,変数順序の明示的指定例は節3.1の実行例5に示す. 方程式\(F(x,y,z)=0\)の求解関数としては,\({\rm Maxima}\)の標準関数\({\rm algsys}\)を用いる. 数式処理における多項式方程式の求解は求解変数の次数に関して,通常4次までに制限される.用いる求解関数\({\rm algsys}\)においてもこの制限を受ける.また,4次以下の次数であっても係数が複雑な場合は求解に失敗するが, 逆に,5次以上であっても探索的な因数分解に成功する場合には正しく解を求める場合もある. また,1変数多項方程式においては係数が浮動小数でない場合には厳密解を求めようとするが, これに失敗した場合には数値的解法に切り替え近似解(数値解,浮動小数解)を返す(横田(2007)参照). この数値解法を許せば,第1変数の求解に関しては4次までの次数制限は解除される. また,解を得るには境界方程式\(F(x,y,z)=0\)から最終変数\(z\)を消去した消去方程式\(F(x,y)=0\)を得る必要がある.このための処理関数として\({\rm Maxima}\)の標準関数\({\rm eliminate}\)を用いる. この関数は,終結式を求めることで 変数消去を行い,結果を多項式で返す(結果はグレブナー基底に基づく最小多項式と一致する).
2.1 変数消去に基づく等式解
与えられた不等式が \(f_l(x,y,z) \leq f(x,y,z) < f_r(x,y,z)\) で表せる場合(第1不等号に等号が含まれ,第2不等号には等号が含まれない場合)について示す.
項目1) 境界方程式 \[ f_1(x,y,z) = f(x,y,z) - f_l(x,y,z)=0, ~~~ f_2(x,y,z) = f(x,y,z) - f_r(x,y,z)=0 \] を生成し,開閉記号を含めたリスト表現 \([[f_1(x,y,z),{\rm c}],[f_2(x,y,z),{\rm o}]]\) を得る.
項目2) 境界方程式\(f_1(x,y,z)=0\)を最終変数\(z\)に関して解き,結果を\(\{[z_{1i}(x,y),\,{\rm c}];~i=1,2,\cdots\}\) とする. 同様に,境界方程式\(f_2(x,y,z)=0\)を\(z\)について解いた結果を\(\{[z_{2i}(x,y),\,{\rm o}];~i=1,2,\cdots\}\) とする. ここで, \(z=z_{1i}(x,y)\)は閉曲面となり, \(z=z_{2i}(x,y)\)は開曲面となる.この処理を Maxima の標準関数 algsys を用いて行う. これらの解 \(z=z(x,y)\) を保存するためのリスト va を準備し,第3変数 \(z\) に対応する va の第3要素 va[3] に追加する.
項目3) 境界方程式\(f_1(x,y,z)=0\)に,これを変数\(z\)で偏微分した方程式 \(f_{1z}(x,y,z)=0\)を加えた連立方程式から変数\(z\)を消去した方程式\(f_1(x,y)\)を得る.次に,消去方程式\(f_1(x,y)=0\)を中間変数\(y\)について解き,結果を\(\{[y_{1i}(x),\,{\rm c}];~i=1,2,\cdots\}\)とする.変数消去には Maxima の標準関数eliminate 関数を用いる. 同様の処理を境界方程式\(f_2(x,y,z)=0\)に対して実行し,結果を\(\{[y_{2i}(x),\,{\rm o}];~i=1,2,\cdots\}\)とする.これらの処理を零点処理と呼ぶことにする.さらに,境界方程式\(f_1(x,y,z)=0\)と\(f_{2}(x,y,z)=0\)からなる連立方程式から変数\(z\)を消去した方程式\(f_{12}(x,y)\)を求め,これを変数\(y\)について解いた結果を\(\{[y_{12i}(x),\,{\rm o}];~i=1,2,\cdots\}\)とする. これは,境界方程式\(f_1(x,y,z)=0\)から定まる閉曲面\(z=z(x,y)\)と\(f_2(x,y,z)=0\)から定まる開曲面\(z=z(x,y)\)の交線\(y=y(x)\)(開交線)を与える.これを交線処理と呼ぶことにする. これらの解\(y=y(x)\)を解リスト va+ の第2要素 va[2]+ に追加する.
項目4) 上記の境界方程式\(f_1(x,y)=0,~f_2(x,y)=0\)および\(f_{12}(x,y)=0\)の各々について,変数\(y\)を消去した方程式を導いた上で変数\(x\)に関して解く零点処理を行い,結果 \(\{[x_{1i},\,{\rm c}];~i=1,2,\cdots\}\), \(\{[x_{2i},\,{\rm o}];~i=1,2,\cdots\}\), \(\{[x_{12i},\,{\rm o}];~i=1,2,\cdots\}\) を得る. 次に,3組(3個の方程式から2個の方程式を取り出す組合せ数)の連立方程式 \(\{f_1(x,y)=0,~f_2(x,y)=0\}\), \(\{f_1(x,y)=0,~f_{12}(x,y)=0\}\),\(\{f_2(x,y)=0,~f_{12}(x,y)=0\}\) の各々に対して交点処理を行い,結果\(\{[x_{(1,2)i},\,{\rm c}];~i=1,2,\cdots\}\), \(\{[x_{(1,12)i},\,{\rm o}];~i=1,2,\cdots\}\),\(\{[x_{(2,12)i},\,{\rm o}];~i=1,2,\cdots\}\) を得る.これらの解を解リスト va+ の第1要素 va[1]+ に追加する.
なお,eliminate 関数の使用 eliminate([f,g],[z])
において,f と g に共通因子がある場合には共通因子を除く必要がある.
2.2 解領域の生成
解領域の生成手順を示す.
- 項目1) 第1変数\(x\)に関する解リストva[1]+の昇順第i順位点を\(x_i\),第i+1順位点を\(x_{i+1}\)とする.
- 項目2) \(x_i\) と \(x_{i+1}\) の中間点 \(x_{(i)}\) で 中間変数\(y=y(x)\)の解リスト va[2] を評価し, 評価値が第j順位である関数を\(y_j(x)\),第j+1順位の関数を\(y_{j+1}(x)\)とし,中間値を\(y_{(j)}\)とする.
- 項目3) 中間値\((x_{(i)},y_{(j)})\)において,最終変数\(z=z(x,y)\)の解リスト va[3] を評価し, 評価値が第k順位である関数を\(z_k(x,y)\),第k+1順位の関数を\(z_{k+1}(x,y)\)とし, 中間値を\(z_{(k)}\)とする.
- 項目4) 中間値\((x_{(i)},y_{(j)},z_{(k)})\)が与不等式を満たせば,セル領域 \[ \rm {\rm on3}(x,x_i,x_{i+1},{\rm oo})*{\rm on3}(y,y_j(x),y_{j+1}(x),{\rm oo})*{\rm on3}(z,z_k(x,y),z_{k+1}(x,y),{\rm zlr}) \] を解領域の1つとする.ここで,最終変数\(z\)の開閉 zlr は va[3] の開閉を用いる.
- 項目5) 上記1)から4)をすべてのセル領域にわたり行う. 結果のリスト表現を LL とする.
LL = [[Ix[1],Iy[1],Iz[1]],…,[Ix[k],Iy[k],Iz[k]]],
ただし Ix[i]=[xl[i],xr[i],xlr[i]], Iy[i]=[yl[i],yr[i],ylr[i]], Iz[i]=[zl[i],zr[i],zlr[i]]以上の処理には,間接ソート関数,添字リストとそのスタック処理を伴う.
2.3 開閉処理
前節で得られた解領域リスト LL において最終変数\(z\)に関する開閉は確定している.本節では,最終変数\(z=z(x,y)\)の開閉と,関数\(z=z(x,y)\)の中間変数\(y\)の境界点\(y_j\)における連続性の評価に基づき,中間変数の開閉を定める手順を採用する.まず,2変数の場合についての手順を示す.
- 項目2-1) LL+に現れる\(x_i\)を1つ固定し,\(x_i\)を右,左境界値にもつLL+の項を抽出し,これをLYLR+とする. \[ \rm {\rm LYLR} = [[[\ell_1,LR_1],[yl_{1},yr_{1},ylr_1]],\, [[\ell_2,LR_2],[yl_{2},yr_{2},ylr_2]],\, \cdots ] \] ここで, \(\ell_i\)はLL+の要素番号を表し,\({\rm LR}_i\)は境界点\(x_i\)からみて左に現れる(\(x_i\)を右境界値にもつ)ときL,右に現れる(\(x_i\)を左境界値にもつ)ときRとする.
- 項目2-2) LYLR+の\(\rm yl_i,~yr_i\)に現れる\(y=y(x)\)の各々について, 左極限値\(\displaystyle y(x_i-)=\lim_{x \rightarrow x_i-0}y(x)\), 右極限値\(\displaystyle y(x_i+)=\lim_{x \rightarrow x_i+0}y(x)\)を求める (右,左極限値は\({\rm Maxima}\)の標準関数\({\rm limit}\)を用いる.極限値が存在しない場合はnullとする). すべての\(y(x)\)の右,左極限値を併合したものを昇順ソートし, 右,左極限値に基づく昇順順位\({\rm P}\)を与える.これをリストLYにまとめる. \[ \rm {\rm LY}=[['y(x),[y(x-),{\rm P}_{-},{\rm lr}_{-}],[y(x+),{\rm P}_{+},{\rm lr}_{+}]],\,\cdots] \] ここで,開閉\(\rm lr_{-}\)は点\(\rm P_{-}\)を通るすべての曲線\(y(x)\)が閉線のとき閉(c), その他のときは開(o)として定まる.開閉\(\rm lr_{+}\)についても同様である.
- 項目2-3) 2-1)のLYLR+に2-2)のLY+の結果を併合し,以下のリストLTAB+を生成する. \[ \rm {\rm LTAB} = [[[\ell_1,LR_1],['yl_1,'yr_1,lr_1], [P_{1l},lr_{1l}],[P_{1r},lr_{1r}],"判定結果"],\,\cdots] \] ここで,\(\rm LR_1=L\)とすると,関数\(\rm yl_1\)が点\(x_i\)の左から点\(\rm P_{1l}\)に近づき,\(\rm lr_{1l}\)は点\(\rm P_{1l}\)の開閉を表す.同様に関数\(\rm yr_1\)が点\(x_i\)の左から点\(\rm P_{1r}\)に近づき,\(\rm lr_{1r}\)は点\(\rm P_{1r}\)の開閉を表す.\(\rm LR_1=R\)の場合は点\(x_i\)の右からの評価に基づく.
- 項目2-4) 境界点\(x_i\)をもつ区間\((x_{i-1},\,x_{i})\),または\((x_i,\,x_{i+1})\)において\(x_i\)を含めるか否かの判定を次の規則に基づき行う.
> - 項目R1) LTAB+に現れる\(x_i\)上の\(y\)の区間\((\rm P_{jl},\,P_{jr})\)において, 飛び越し(\(\rm P_{jl}=P_1\)(第1順位点),\(\rm P_{jr}=P_3\)(第3順位点)であれば\(\rm P_2\)(第2順位点)が飛び越された点となる)がある場合, 飛び越された点にo点があれば飛び越し区間を不採用(\(x_i\)を含めない)とし, 飛び越された点がすべてc点のときは\(x_i\)を含める. また,含める場合には,飛び越された順位点をもつ\({\rm LTAB}\)の項をR1-included(処理済み)とする. >
- 項目R2) 区間\((\rm P_{jl},\,P_{jr})\)が飛び越しのない2点区間の場合は,\(\rm lr_j\)と\(\rm lr_{jl}\),\(\rm lr_{jr}\)の開閉が一致する\({\rm LTAB}\)の項の1ヶ所に\(x_i\)を含め,その他の同一項はR2x(処理済み)とする. >
- 項目R3) 区間\((\rm P_{jl},\,P_{jr})\)が1点区間(同一順位点)である場合は,その点が閉\(({\rm c})\)であれば\(x_i\)を含め, 開\(({\rm o})\)であれば含めないとする.また,同一の1点区間をもつ項はR3x(処理済み)とする. 上記の判定結果を\({\rm LTAB}\)の各項の最終要素に書き込む.
- 項目2-5) \({\rm LTAB}\)に上記規則を適用し,\({\rm LL}\)を更新する.例えば, \({\rm LL[1] = [[x5,x1,oo],[y4,y1,co]]}\) として\({\rm x1}\)が含まれると判定されたとき, \({\rm [[x5,x1,oc],[y4,y1,co]]}\)のように更新される.
- 項目2-6) 上記2-1)から2-5)を\({\rm LL}\)に現れるすべての\(x_i\)について繰り返し,開閉処理を終了する.
開閉処理の概要を略図1に示す.
略図1
LL = [[[x5,x1,oo],[y4,y1,co]], 1 <- LLの項番号
[[x1,x2,oo],[y4,y3,co]], 2
[[x1,x2,oo],[y2,y1,oo]], 3
[[x2,x3,oo],[y4,y1,co]], 4
[[x3,x4,oo],[y6,y5,cc]], 5
[[x3,x4,oo],[y4,y1,co]], 6
[[x4,x6,oo],[y4,y1,co]]] 7
<case-1> x_i = x1 = -4.3414 に固定 <case-2> x_i = x2 = -2.287623 に固定
LTAB=[[[1,L],[y4,y1,co],[P1,c],[P2,o],"R2"], LTAB=[[[2,L],[y4,y3,co],[P1,c],[P2,o],"R2"],
[[2,R],[y4,y3,co],[P1,c],[P2,o],"R2x"], [[3,L],[y2,y1,oo],[P2,o],[P3,o],"R2"],
[[3,R],[y2,y1,oo],[P3,o],[P3,o],"R3x"]] [[4,R],[y4,y1,co],[P1,c],[P3,o],"R1x"]]
y1=y1(x)は点x_1において不連続
P3:o---y1:o <ーR3x y1:o--- P3:o---y1:o
P3:o---y2:o R2 -> ] |
| y2:o ---P2:o
y1:o ---P2:o---y3:o y3:o ---P2:o <---R1x
R2 -> ] | <ーR2x R2 -> ] |
y4:c ---P1:c---y4:c y4:c ---P1:c---y4:c
| |
x_1=-4.3414 x_2=-2.2876略図1では,領域生成処理によってリスト\({\rm LL}\)が得られたとして,境界点\(x_1\)の開閉処理をcase-1+に,境界点\(x_2\)の開閉処理をcase-2+に示した.case-1+においては\({\rm LL}\)の第1要素において\(x_1\)が含まれ,case-2+では\({\rm LL}\)の第2,第4要素において\(x_2\)が含まれる.略図1で示した開閉処理は節2.4の実行例2に現れる. 注意点としては以下の事項が挙げられる.
- 項目c1)
開閉処理には一意に定められる場合とそうでない場合が存在する.上記
+の場合において,区間\([{\rm P}1,{\rm P}2)\)は \({\rm [[x5=minf,x1,oc],[y4,y1,co]]}\) とするか, \({\rm [[x1,x2,co],[y4,y3,co]]}\) の自由度をもつ.その場合には規則 R2) に従い,最初に検出された区間 \({\rm [[x5=minf,x1,oc],}\) \({\rm [y4,y1,co]]}\) が採用される. - 項目c2) 第1変数\(x\)の境界点は\(x_1=-4.3414\),\(x_2=-2.2876\)のように近似解(浮動小数解)として得られている.これは求解関数\({\rm algsys}\)が厳密解を得られないと判断したときに近似解法(数値解法)に切り替えて求解処理を行うことによる.あくまでも厳密解を得たい場合には大域変数\({\rm algexact:true}\)として実行すればよいが,厳密解が得られる問題は限られ,また,多大の計算機資源を必要とするため現実的ではない.本稿では,${} \(~(Maxima+のデフォルト) として処理する.そのとき, 左極限値\)y(x_i-)={x x_i-0}y(x)\(, 右極限値\)y(x_i+)={x x_i+0}y(x)\(を求める際に,微小正数\)$ を用い,\(x_i-0\)を\(x_i-\varepsilon-0\),\(x_i+0\)を\(x_i+\varepsilon+0\) として処理される.
次に上記の開閉処理を3変数の場合に拡張する.
- 項目3-0) 3変数の場合,解リスト \({\rm LL}\) は以下の形式で表せる. \[ \begin{array}{ll} {\rm LL} = & \rm [[[xl_1,xr_1,xlr_1],[yl_1,yr_1,ylr_1],[zl_1,zr_1,zlr_1]],~ \\[1ex] & \rm ~~[[xl_2,xr_2,xlr_2],[yl_2,yr_2,ylr_2],[zl_2,zr_2,zlr_2]],\, \cdots] \nonumber \end{array} \] ここで,最終変数\(z\)に関する開閉\(\rm zlr_i\)は確定している.
- 項目3-1) LL+に現れる\(y_j\)を1つ固定し,\(y_j\)を右,左境界値にもち,かつ共通の\({\rm Ix =[xl,xr,xlr]}\)をもつLL+の項を抽出し,これをLZLR+とする. \[ \rm {\rm LZLR} = [[[\ell_1,LR_1],[zl_{1},zr_{1},zlr_1]],\, [[\ell_2,LR_2],[zl_{2},zr_{2},zlr_2]],\, \cdots ] \] ここで, \(\ell_i\)はLL+の要素番号を表し,\({\rm LR}_i\)は境界点\(y_j\)からみて左に現れる(\(y_j\)を右境界値にもつ)ときL,右に現れる(\(y_j\)を左境界値にもつ)ときRとする.
- 項目3-2) LZLR+の\(\rm zl_k,~zr_k\)に現れる\(z=z(x,y)\)の各々について,\(x_{(m)}\)を\({\rm Ix =[xl,xr,xlr]}\)に現れる\({\rm xl}\),\({\rm xr}\)の中間値と定めると,\(y_j=y_j(x_{(m)})\)は値(関数値)となり, 左極限値\(\displaystyle z(x_{(m)},y_j-)=\lim_{y \rightarrow y_j-0}z(x_{(m)},y)\), 右極限値\(\displaystyle z(x_{(m)},y_j+)=\lim_{y \rightarrow y_j+0}z(x_{(m)},y)\)を評価できる (極限値が存在しない場合はnullとする). すべての\(z(x_{(m)},y)\)の右,左極限値を併合したものを昇順ソートし, 右,左極限値に基づく昇順順位\({\rm P}\)を与える.これをリストLZにまとめる. \[ \rm {\rm LZ} = [['z(x,y),[z(x_{(m)},y-),{\rm P}_{-},{\rm lr}_{-}],[z(x,y+),{\rm P}_{+},{\rm lr}_{+}]],\,\cdots] \] ここで,開閉\({\rm lr}_{-}\)は点\({\rm P}_{-}\)を通るすべての曲線\(z(x_{(m)},y)\)が閉線のとき閉(c), その他のときは開(o)として定まる.開閉\({\rm lr}_{+}\)についても同様である.
- 項目3-3) 3-1)の LZLR に3-2)の LZ の結果を併合し,以下の LTAB を生成する. \[ \rm {\rm LTAB} = [[[\ell_1,LR_1],['zl_1,'zr_1,lr_1], [P_{1l},lr_{1l}],[P_{1r},lr_{1r}],"判定結果"],\,\cdots] \]
- 項目3-4) 境界\(y_j\)をもつ区間\((y_{j-1},\,y_{j})\),または\((y_j,\,y_{j+1})\)において\(y_j\)を含めるか否かの判定を前述の規則 R1),,R2),,R3)に基づき行う.
- 項目3-5) 3-1)において\(y_j\)を1つ固定した上で,別の共通\({\rm Ix = [xl,xr,xlr]}\)をもつ\({\rm LL}\)の項があれば, 3-1)から3-4)を繰り返す. また, \(y_j\)に関しても同様に繰り返す.
- 項目3-6) 3-1)から3-5)によって中間変数\(y=y(x)\)に関する開閉処理を終了する. この中間変数\(y\)の開閉結果を用いて,第1変数\(x\)の開閉処理を2変数の場合に従って行う.
2.4 実行例
節2.1から節2.3の手順を以下の例で確かめる.
◎ 2変数不等式の例1: 不等式 \[
1 \leq x^2+2\,x\,y+y^3 < 9
\] の求解結果を図1および実行例2に示す.
実行例2
(%i1) on3ineq([x^2+2*x*y+y^3,1,9,co]);
LL = [[['V[1][5],'V[1][1],oc],['V[2][4],'V[2][1],co]], <- 解領域のリスト表現
[['V[1][1],'V[1][2],oc],['V[2][4],'V[2][3],co]],
[['V[1][1],'V[1][2],oc],['V[2][2],'V[2][1],oo]],
[['V[1][2],'V[1][3],oc],['V[2][4],'V[2][1],co]],
[['V[1][3],'V[1][4],oc],['V[2][6],'V[2][5],cc]],
[['V[1][3],'V[1][4],oc],['V[2][4],'V[2][1],co]],
[['V[1][4],'V[1][6],oo],['V[2][4],'V[2][1],co]]]
, where
V[ 1 ]= [-4.3414023,-2.2876238,-2.0459579,-0.652667,minf,inf] <- 第1変数xの境界点
V[ 2 ]= [(sqrt/Product(2)-Quotient)^(1/3)-2*x/(3*Expt), <- 最終変数y=y(x)の簡易表現
(-Quotient-1/2)*(Quotient+Negterm)^(1/3)-2*Sum(2)*x/(3*Expt), (標準関数 reveal による)
(Product(2)/2-1/2)*(Quotient+Negterm)^(1/3)-2*Sum(2)*x/(3*Expt),
(sqrt/Product(2)-Quotient)^(1/3)-2*x/(3*Expt),
(-Quotient-1/2)*(Quotient+Negterm)^(1/3)-2*Sum(2)*x/(3*Expt),
(Product(2)/2-1/2)*(Quotient+Negterm)^(1/3)-2*Sum(2)*x/(3*Expt),minf,inf] - Maxima 実行例2
on3ineq([x^2+2*x*y+y^3,1,9,co],'noview, 'resultonly, 'nooutsum,
'file_name="figs/jjss-ex2");## ~/bin/go TMP/tmp_lang/chunk-3.mxl > TMP/tmp_lang/chunk-3.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl
## on3ineq([x^2+2*x*y+y^3,1,9,co],'noview,'resultonly,'nooutsum,
## 'file_name = "figs/jjss-ex2")
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl"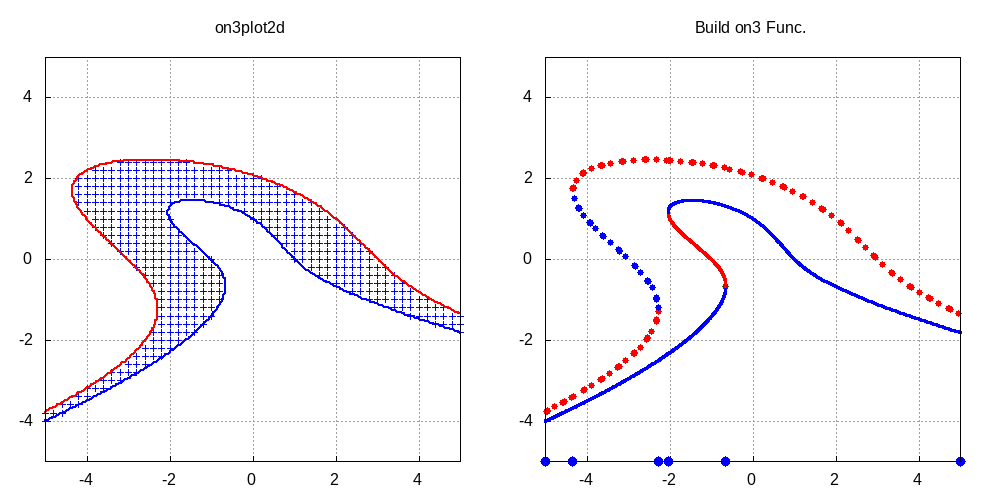
実行例2の LL は不等式の解領域のリスト表現を表す.V[1][5]=minf は
\(x_5=-\infty\) を表し,
V[2][4]=(sqrt/Product(2)-Quotient)^(1/3)-2*x/(3*Expt) は
\(y_4="y_4(x)\) の簡易表現を表す.
簡易表現で表された最終変数 \(y\) の関数
\(y_j=y_j(x)\)
は整理すると以下で表せる.
\[ \small \begin{array}{ll} {\rm 'V[2][1]:} & y_1(x) = a(x) - \displaystyle \frac{2\,x}{3\,a(x)}\, \\[1.2ex] {\rm 'V[2][2]:} & y_2(x) = \displaystyle \frac{-\sqrt{3}\,i-1}{2} a(x) - \frac{\sqrt{3}i-1}{2}\,\frac{2\,x}{3\,a(x)} \quad (i は虚数単位を表す)\\[1.2ex] {\rm 'V[2][3]:} & y_3(x) = \displaystyle \frac{\sqrt{3}\,i-1}{2}\,a(x) - \frac{-\sqrt{3}i-1}{2} \,\frac{2\,x}{3\, a(x)} \\[1.2ex] {\rm 'V[2][4]:} & y_4(x) = b(x) - \displaystyle \frac{2\,x}{3\,b(x)}\, \\[1.2ex] {\rm 'V[2][5]:} & y_5(x) = \displaystyle \frac{-\sqrt{3}\,i-1}{2} b(x) - \frac{\sqrt{3}i-1}{2}\,\frac{2\,x}{3\,b(x)} \\[1.2ex] {\rm 'V[2][6]:} & y_6(x) = \displaystyle \frac{\sqrt{3}\,i-1}{2}\,b(x) - \frac{-\sqrt{3}i-1}{2} \,\frac{2\,x}{3\, b(x)} \\[1.2ex] ただし & a(x) = \displaystyle \left(\frac{\sqrt{27\,x^4+32\,x^3-486\,x^2+2187}}{2\cdot3^{3/2}} - \frac{x^2-9}{2}\right)^{1/3}, \quad b(x) = \displaystyle \left(\frac{\sqrt{27\,x^4+32\,x^3-54\,x^2+27}}{2\cdot3^{3/2}} - \frac{x^2-1}{2}\right)^{1/3} \\[2ex] \end{array} \]
よって,LL1要素は \({\rm on3}(x,-\infty,-4.34,{\rm oc})*{\rm on3}(y,y_4(x),y_1(x),{\rm co})\) を表す. 解領域のリスト表現は \(y_j(x)\) が複雑な式になるときに \({\rm on3}\) 関数表現に変えて用いることにする. 関数 \(y_1(x)\) は \(x=x_1≒-4.34\) で不連続であり,\(y_4(x)\) は \(x=x_3≒-2.04\) で不連続となる. 図1における左図は境界方程式の陰関数表示に基づく描画に,図示領域内の \(50\times50\) の分割点において与不等式を満たすとき \(+\)を 表示した.右図は不等式求解関数に基づく区間陽関数表示で,実線は閉を破線は開を表し,横軸上の \(\bullet\) は境界点 \(x_i\) を表す.
◎ 2変数不等式の例2:
境界方程式に自己交差を含む不等式(近藤他(2005)参照) \[-1 < x^2-y^2-(x^2+y^2)^2 \leq 0
\] の求解結果を実行例3および図2に示す.
実行例 3
(%i1) on3ineq([x^2-y^2-(x^2+y^2)^2,-1,0,oc]);
(%o1) on3(x,-sqrt(sqrt(5)+1)/sqrt(2),-1,oc)*on3(y,-sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),
sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),oo)
+on3(x,1,sqrt(sqrt(5)+1)/sqrt(2),co)*on3(y,-sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),
sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),oo)
+on3(x,0,1,oo)*on3(y,-sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),
-sqrt(sqrt(8*x^2+1)-2*x^2-1)/sqrt(2),oc)
+on3(x,-1,0,oc)*on3(y,-sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),
-sqrt(sqrt(8*x^2+1)-2*x^2-1)/sqrt(2),oc)
+on3(x,0,1,oo)*on3(y,sqrt(sqrt(8*x^2+1)-2*x^2-1)/sqrt(2),
sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),co)
+on3(x,-1,0,oc)*on3(y,sqrt(sqrt(8*x^2+1)-2*x^2-1)/sqrt(2),
sqrt(sqrt(8*x^2+5)-2*x^2-1)/sqrt(2),co)
-on3(x,0,0,cc)*on3(y,0,0,cc)
\includegraphics[width=24em,height=17em]{./H1a-1.eps}
\includegraphics[width=24em,height=17em]{./H1a-2.eps}
\caption{陰関数表示{\sc \footnotesize (左図)}と求解関数表示{\sc \footnotesize (右図)}のグラフ}- Maxima 実行例3
on3ineq([[x^2-y^2-(x^2+y^2)^2,-1,0,oc]],'title = "ex3:H1a",
'xrange = [-1.5,1.5],'yrange = [-1.5,1.5],
'file_name = "figs/jjas-ex3",'noview,
'resultonly,'nooutsum);## ~/bin/go TMP/tmp_lang/chunk-4.mxl > TMP/tmp_lang/chunk-4.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-4.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-4.mxl
## on3ineq([[x^2-y^2-(x^2+y^2)^2,-1,0,oc]],'title = "ex3:H1a",'xrange = [-1.5,1.5],
## 'yrange = [-1.5,1.5],'file_name = "figs/jjas-ex3",'noview,'resultonly,'nooutsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-4.mxl"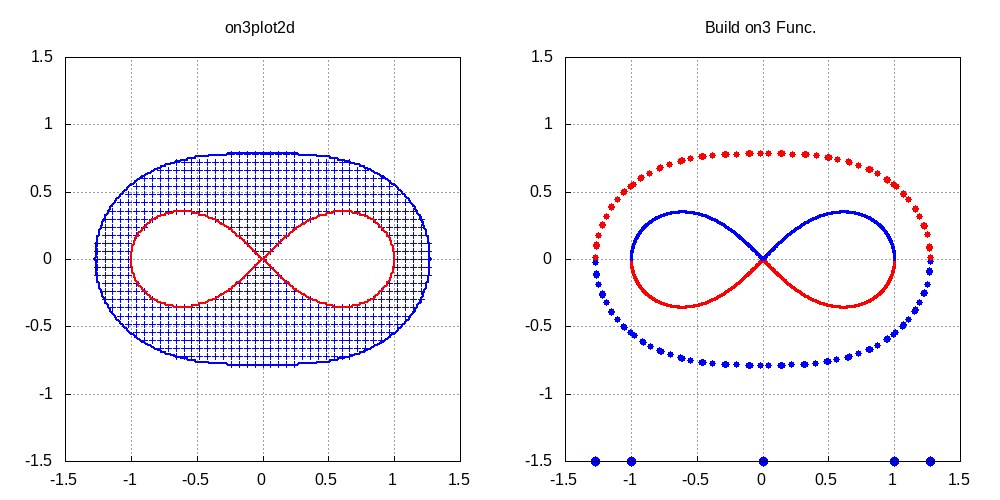
◎ 3変数不等式の例:
3変数不等式の開閉処理を確かめるために,不等式 \[1 \leq x^2+y^2+z^2 < 9
\] に適用した結果を実行例4に示す.
実行例 4
(%i1) on3ineq([x^2+y^2+z^2,1,9,co]); LLの要素番号
LL = [[['V[1][1],'V[1][2],oc],['V[2][3],'V[2][4],oo],['V[3][3],'V[3][4],oo]], 1
[['V[1][2],'V[1][3],oo],['V[2][3],'V[2][1],oc],['V[3][3],'V[3][4],oo]], 2
[['V[1][2],'V[1][3],oo],['V[2][1],'V[2][2],oo],['V[3][3],'V[3][1],oc]], 3
[['V[1][2],'V[1][3],oo],['V[2][1],'V[2][2],oo],['V[3][2],'V[3][4],co]], 4
[['V[1][2],'V[1][3],oo],['V[2][2],'V[2][4],co],['V[3][3],'V[3][4],oo]], 5
[['V[1][3],'V[1][4],co],['V[2][3],'V[2][4],oo],['V[3][3],'V[3][4],oo]]] 6
, where
V[ 1 ]= [-3,-1,1,3,minf,inf]
V[ 2 ]= [-sqrt(1-x^2),sqrt(1-x^2),-sqrt(9-x^2),sqrt(9-x^2),minf,inf]
V[ 3 ]= [-sqrt(-y^2-x^2+1),sqrt(-y^2-x^2+1),-sqrt(-y^2-x^2+9),sqrt(-y^2-x^2+9),minf,inf]
(%o1) `on3(x,1,3,co)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo) 6
*on3(z,-sqrt(-y^2-x^2+9),sqrt(-y^2-x^2+9),oo)
+on3(x,-3,-1,oc)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo) 1
*on3(z,-sqrt(-y^2-x^2+9),sqrt(-y^2-x^2+9),oo)
+on3(x,-1,1,oo)*on3(y,-sqrt(9-x^2),-sqrt(1-x^2),oc) 2
*on3(z,-sqrt(-y^2-x^2+9),sqrt(-y^2-x^2+9),oo)
+on3(x,-1,1,oo)*on3(y,sqrt(1-x^2),sqrt(9-x^2),co) 5
*on3(z,-sqrt(-y^2-x^2+9),sqrt(-y^2-x^2+9),oo)
+on3(x,-1,1,oo)*on3(y,-sqrt(1-x^2),sqrt(1-x^2),oo) 3
*on3(z,-sqrt(-y^2-x^2+9),-sqrt(-y^2-x^2+1),oc)
+on3(x,-1,1,oo)*on3(y,-sqrt(1-x^2),sqrt(1-x^2),oo) 4
*on3(z,sqrt(-y^2-x^2+1),sqrt(-y^2-x^2+9),co)- Maxima 実行例4
on3ineq([[x^2+y^2+z^2,1,9,co]],'noview,'noplot, 'outsum);## ~/bin/go TMP/tmp_lang/chunk-5.mxl > TMP/tmp_lang/chunk-5.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl
## on3ineq([[x^2+y^2+z^2,1,9,co]],'noview,'noplot,'outsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl"実行例4における結果のリスト表現と関数表現の項の順序は一致しない(関数表現において\({\rm Maxima}\)の項表示順序規則の影響を受ける為).解リスト LL の要素番号と解の関数表現における対応を示す.
3. その他の対応
3.1 縮退解領域(孤立点,孤立線)への対応
与えられた不等式の解に,孤立点や孤立線が含まれる場合の対応について考える. 与不等式から得られる境界方程式は, \[[[f_1(x,y,z)=0,\,{\rm c}],~[f_2(x,y,z)=0,\,{\rm o}]]\] の様に表せる.この場合には,方程式 \(f_1(x,y,z)=0\) のみの零点処理となり,解法としては,方程式 \(f_1(x,y,z)=0\) にこれを変数 \(x,y,z\) でそれぞれ偏微分した方程式 \(f_{1x}=0,f_{1y}=0,f_{1z}=0\) を加えた連立方程式 \([f_{1}=0,f_{1x}=0,f_{1y}=0,f_{1z}=0]\) を変数 \((x,y,z)\) について解くことから出発する(齋藤他(2003)参照).続いて,連立方程式 \([f_{1}=0,f_{1x}=0,f_{1y}=0]\),\([f_{1}=0,f_{1x}=0]\),\([f_{1}=0]\) を変数 \((x,y,z)\) について解くことを繰り返す. 求解関数として \({\rm algsys}\) を用い,結果を返さない場合に対応する為に \({\rm errcatch}\) とともに用いる.結果をリスト \([[x=x_1,\,y=y_2,\,z=z_1],\,[x=x_2,\,y=y_2,\,z=z_2],\,\cdots]\) として得る. 結果において,補助変数を伴った解の処理,複素数表現処理(解に \([x=x,\,y=y_o+i(x-x_o)]\) が現れたとき \([x=x_o,\,y=y_o]\) に変換する処理),完全2次形式処理(解に \([x=x,\,y=y,\,z=z_o+\sqrt{-x^2+2\,x_o\,x-y^2+2\,y_o\,y+x_o^2+y_o^2}]\) が現れたとき \([x=x_o,\,y=y_o,\,z=z_o]\) に変換する処理)を必要とする. また,境界方程式が \([[f_1(x,y,z)=0,\,{\rm c}],~[f_2(x,y,z)=0,\,{\rm c}]]\) の様に表せる場合には,方程式 \(f_1(x,y,z)=0\) の零点処理に加えて方程式 \(f_2(x,y,z)=0\) の零点処理を行い,さらに両方程式の交点処理が必要となる.交点処理においては,連立方程式 \([f_{1}=0,\,f_2=0,\,f_{1x}=0,\,f_{2x}=0,\,f_{1y}=0,\,f_{2y}=0,\,f_{1z}=0,\,f_{2z}=0]\) から出発して,\([f_{1}=0,\,f_2=0,\,f_{1x}=0,\,f_{2x}=0,\,f_{1y}=0,\,f_{2y}=0,\,f_{1z}=0]\),\([f_{1}=0,\,f_2=0,\,f_{1x}=0,\,f_{2x}=0,\,f_{1y}=0,\,f_{2y}=0]\),\(\cdots\),\([f_{1}=0,\,f_2=0]\) を変数 \((x,\,y,\,z)\) について解くことを繰り返す. 以上の処理を実行する関数を \({\rm salgall()}\) としてまとめる.その実行例を実行例5に示す.
実行例 5
(%i1) h(x,y) := 93392896/15625*x^6 <- (近藤他(2005),齋藤他(2003,p.81)参照)
+(94359552/625*y^2+91521024/625*y-249088/125)*x^4
+(1032192/25*y^4-36864*y^3-7732224/25*y^2-207360*y+770048/25)*x^2
+65536*y^6+49152*y^5-135168*y^4-72704*y^3+101376*y^2+27648*y-27648$
(%i2) salgall(h(x,y),[y,x]); <- 方程式 h(x,y)=0 の同時解を変数順序 [y,x] を指定して求める
(%o2) [[y = -386/351,x = -35*sqrt(14)/351],[y = -386/351,x = 35*sqrt(14)/351],
[y = -1,x = 0],[y = -41/76,x = -5*7^(3/2)/(19*2^(3/2))],
[y = -41/76,x = 5*7^(3/2)/(19*2^(3/2))],[y = 3/4,x = 0],
[y = 1.4555639,x = -0.891117],[y = 1.4555639,x = 0.891117]]
\includegraphics[width=30em,height=19em]{./H2-2.eps}
\caption{$h(x,y)=0$ の零点描画}- 実行例5
h(x,y) := 93392896/15625*x^6 /* <- (近藤他(2005),齋藤他(2003,p.81)参照) */
+(94359552/625*y^2+91521024/625*y-249088/125)*x^4
+(1032192/25*y^4-36864*y^3-7732224/25*y^2-207360*y+770048/25)*x^2
+65536*y^6+49152*y^5-135168*y^4-72704*y^3+101376*y^2+27648*y-27648$
salgall(h(x,y),[y,x]); /* <- 方程式 h(x,y)=0 の同時解を変数順序 [y,x] を指定して求める */
on3ineq([[h(x,y),0,0,cc]],'title = "ex4:H2",
'xrange = [-1.5,1.5],'yrange = [-1.5,1.5],
'file_name = "figs/jjas-ex5",'noview,
'resultonly,'nooutsum);## ~/bin/go TMP/tmp_lang/chunk-6.mxl > TMP/tmp_lang/chunk-6.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl
## h(x,y):=(93392896/15625)*x^6+((94359552/625)*y^2+(91521024/625)*y+(-249088)/125)*x^4
## +((1032192/25)*y^4-36864*y^3+((-7732224)/25)*y^2+(-207360)*y+770048/25)*x^2+65536*y^6
## +49152*y^5+(-135168)*y^4+(-72704)*y^3+101376*y^2+27648*y-27648
## salgall(h(x,y),[y,x])
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3ineq([[h(x,y),0,0,cc]],'title = "ex4:H2",'xrange = [-1.5,1.5],'yrange = [-1.5,1.5],
## 'file_name = "figs/jjas-ex5",'noview,'resultonly,'nooutsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl"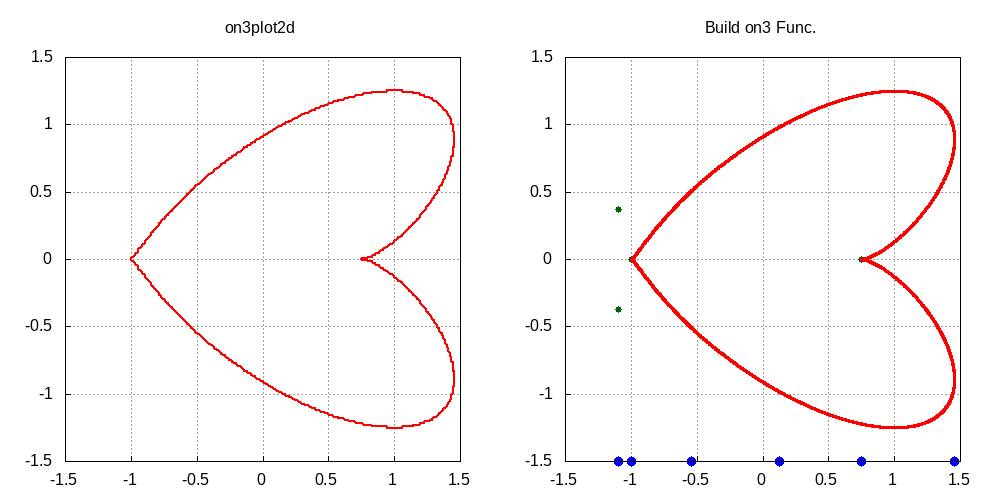
関数 \(h(x,y)\) (近藤他(2005),齋藤他(2003)参照)では,変数 \(y\) に関する次数の並びは\((6,5,4,3,2,1)\) で,変数 \(x\) に関しては \((6,4,2)\) である.よって,\(t=x^2\) と見なせば最高次数は3と見なせる.この為,(%i2) では,変数順序を [y,x] のように指定し,変数 \(x\) の変数消去を先に実行している. また,方程式 \(h(x,y)=0\) を不等式 \(0 \leq h(x,y) \leq 0\) と見なし, 不等式求解関数 \({\rm on3ineq([h(x,y),0,0,cc],\,'varl=[y,x])}\) を実行した結果を図3に示す. ここで,引数 ’varl=[y,x] は変数順序指定を表し,図3の横軸は \(y\),縦軸は \(x\) を表す.
3.2 有理式への対応
多変数多項式を分子,分母にもつ有理式に関する不等式 \[ \frac{f_{ln}(x,y,z)}{f_{ld}(x,y,z)} \leq \frac{f_n(x,y,z)}{f_d(x,y,z)} < \frac{f_{rn}(x,y,z)}{f_{rd}(x,y,z)} \] を解くことを考える.このとき,境界方程式は \[ f_{l}(x,y,z) = f_{n} \times f_{ld} - f_{ln} \times f_{d} =0 \] \[ f_{r}(x,y,z) = f_{n} \times f_{rd} - f_{rn} \times f_{d} =0 \] で表せ,開閉記号を含めたリスト表現\([[f_{l}(x,y,z),\,{\rm c}],\,[f_{r}(x,y,z)=0,\,{\rm o}]]\)を得る. また,方程式 \[ f_{s}(x,y,z) = f_{ld} \times f_{d} \times f_{rd} = 0 \] を特異方程式(分母を零にする特異点,特異線,等を表す)と呼び,リスト表現を\([f_{s}(x,y,z)=0,\,{\rm s}]\) とする.このとき,\([[f_{l}(x,y,z),\,{\rm c}],\,[f_{r}(x,y,z)=0,\,{\rm o}]]\)の零点処理,交点処理に加えて \([f_{s}(x,y,z)=0,\,{\rm s}]\)の零点処理,\([f_{s}(x,y,z)=0,\,{\rm s}]\)と\([[f_{l}(x,y,z),\,{\rm c}],\,[f_{r}(x,y,z)=0,\,{\rm o}]]\)の交点処理が追加される.この交点処理の結果の開閉記号には\({\rm s}\)を用い,開閉処理対象から除外される. 不等式 \[ \displaystyle \frac{1}{x-1} \leq \frac{x^2-y}{(x-1)(y-2)} < \frac{1}{y-2} \] の求解結果を実行例6および図4に示す.\
実行例 6
(%i1) on3ineq([(x^2-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co]);
(%o1) on3(x,minf,-sqrt(2),oc)*on3(y,(x^2+2)/2,x^2-x+1,co)
+on3(x,(sqrt(5)+1)/2,2,co)*on3(y,x^2-x+1,(x^2+2)/2,oc)
+on3(x,0,1,oo)*on3(y,x^2-x+1,(x^2+2)/2,oc)
+on3(x,sqrt(2),(sqrt(5)+1)/2,oo)*on3(y,2,(x^2+2)/2,oc)
+on3(x,-sqrt(2),-(sqrt(5)-1)/2,oo)*on3(y,2,x^2-x+1,oo)
\caption{陰関数表示{\sc \footnotesize (左図)}と求解関数表示{\sc \footnotesize (右図)}のグラフ}- 実行例6
on3ineq([[(x^2-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co]],
'title = "ex6:S1",'xrange = [-4,4],'yrange = [0,5],
'file_name = "figs/jjas-ex6",
'noview, 'resultonly,'nooutsum);## ~/bin/go TMP/tmp_lang/chunk-7.mxl > TMP/tmp_lang/chunk-7.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-7.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-7.mxl
## on3ineq([[(x^2-y)/((x-1)*(y-2)),1/(x-1),1/(y-2),co]],'title = "ex6:S1",'xrange = [-4,4],
## 'yrange = [0,5],'file_name = "figs/jjas-ex6",'noview,'resultonly,'nooutsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-7.mxl"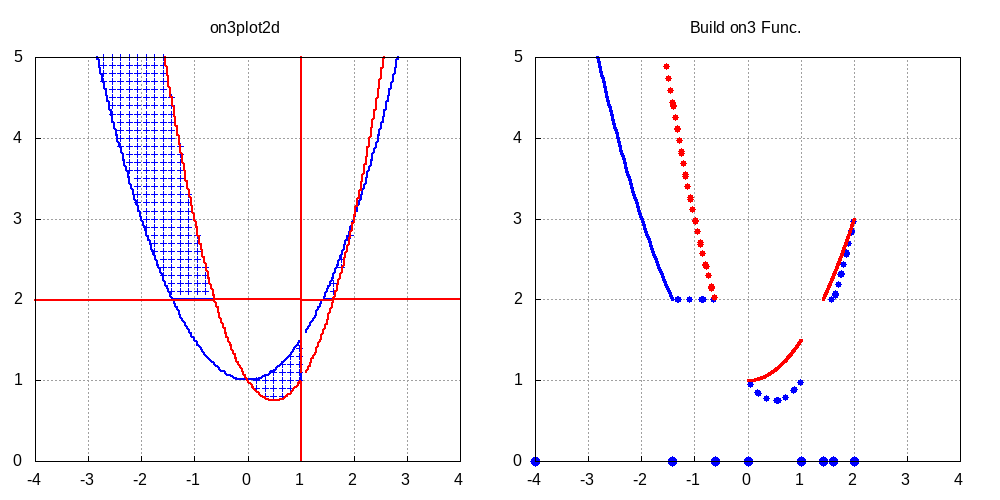
3.3 連立不等式への対応
連立不等式 \[ \left\{ \begin{array}{l} f_{1l}(x,y,z) \leq f_{1}(x,y,z) < f_{1r}(x,y,z) \\[1ex] f_{2l}(x,y,z) \leq f_{2}(x,y,z) < f_{2r}(x,y,z) \nonumber \end{array} \right. \] を解くことを考える.このとき,境界方程式は \[ \begin{array}{ll} F_{1l}(x,y,z) = f_1 - f_{1l}=0, & F_{1r}(x,y,z) = f_1 - f_{1r} = 0, \\[1ex] F_{2l}(x,y,z) = f_2 - f_{2l}=0, & F_{2r}(x,y,z) = f_2 - f_{2r} = 0 \nonumber \end{array} \] で表せ,開閉記号を伴った以下のリスト表現を得る. \[ \rm {\rm FL} = [[F_{1l}(x,y,z) = 0, {\rm c}],\, [F_{1r}(x,y,z) = 0, {\rm o}],\, [F_{2l}(x,y,z) = 0, {\rm c}],\, [F_{2r}(x,y,z) = 0, {\rm o}]] \] 次に,リスト\({\rm FL}\)から2個の要素を取り出す全組み合わせ \[ \rm {\rm FF}=[[F_{1l},F_{1r}],\,[F_{1l},F_{2l}],\,[F_{1l},F_{2r}],\, [F_{1r},F_{2l}],[F_{1r},F_{2r}],\, [F_{2l},F_{2r}]] \] を生成し,その一つを\({\rm [F_a,F_b]}\)で表す.このとき,連立不等式の解は,以下の処理
- 項目1) \(F_a(x,y,z)=0\)に対して零点処理を行う.
- 項目2) \(F_b(x,y,z)=0\)に対して零点処理を行う.
- 項目3) \(F_a(x,y,z)=0\),\(F_b(x,y,z)=0\)に対して交点処理を行う.
をリスト\({\rm FF}\)の全要素に対して行うことで得られる.使用例として連立不等式 \[ \left\{ \begin{array}{l} (x-1)(x-5)+5 \leq y < -(x-1)(x-5)+5 \\[1ex] 5-x \leq y < x+1 \nonumber \end{array} \right. \] の求解例を実行例7および図5に示す.
実行例 7
(%i1) on3ineq([[y,(x-1)*(x-5)+5,-(x-1)*(x-5)+5,co],[y,5-x,x+1,co]]);
(%o1) on3(x,(sqrt(21)+5)/2,5,oo)*on3(y,x^2-6*x+10,6*x-x^2,co)
+on3(x,(sqrt(5)+5)/2,(sqrt(21)+5)/2,oc)*on3(y,x^2-6*x+10,x+1,co)
+on3(x,2,(sqrt(5)+5)/2,oc)*on3(y,5-x,x+1,co) - 実行例7
on3ineq([[y,(x-1)*(x-5)+5,(-(x-1))*(x-5)+5,co],
[y,(-(x-2))+3,(x-2)+3,co]],'title = "ex6:A1",
'xrange = [0,6],'yrange = [-2,10],
'file_name = "figs/jjas-ex7",'noview,
'resultonly,'nooutsum);## ~/bin/go TMP/tmp_lang/chunk-8.mxl > TMP/tmp_lang/chunk-8.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl
## on3ineq([[y,(x-1)*(x-5)+5,(-(x-1))*(x-5)+5,co],[y,(-(x-2))+3,(x-2)+3,co]],
## 'title = "ex6:A1",'xrange = [0,6],'yrange = [-2,10],'file_name = "figs/jjas-ex7",
## 'noview,'resultonly,'nooutsum)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl"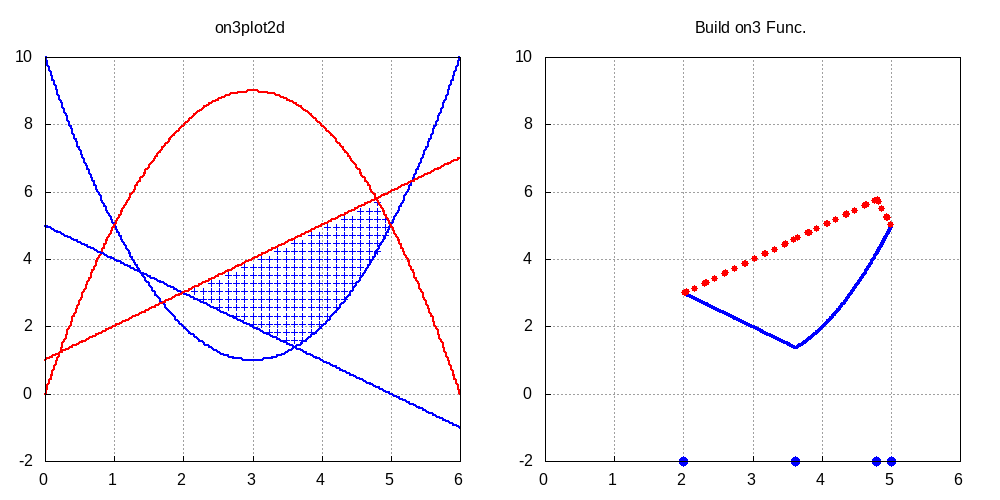
%[6] 連立不等式への対応
% f1l(x,y,z) <= f1(x,y,z) < f1r(x,y,z) かつ
% f2l(x,y,z) <= f2(x,y,z) < f2r(x,y,z)
%
% [[F1l(x,y,z) = f1 - f1l, c], [F1r(x,y,z) = f1 - f1r, o],
% [F2l(x,y,z) = f2 - f2l, c], [F2r(x,y,z) = f2 - f2r, o]]
%
% FL : [F1l,F1r,F2l,F2r]
% FF : full_listfy(powerset(fullsetify(FL))) <- FL から2個を取り出す組み合わせ
% -> [[F1l,F1r],[F1l,F2l],[F1l,F2r], [F1r,F2l],[F1r,F2r], [F2l,F2r]]
% -> {[FA,FB]}
% 上記 [FA,FB] に対して以下の操作を行う.
% (1) FA(x,y,z)=0 を解く
% ansz : algsys([FA],[z]) --> [z=z1(x,y),z=z2(x,y),...]
% [ansy,fy] : elimalg1(FA,z,y) <- FA から変数zを消去した後に変数yについて解く
% fy : eliminate([FA,diff(FA,z)],[z]),
% ansy : algsys([fy],[y])
% [ansx,fx] : elimalg1(fy,y,x) <- fyから変数yを消去した後に変数xについて解く
% fx : eliminate([fy,diff(fy,y)],[y])
% ansx : algsys([fx],[x])
% (2) FB(x,y,z) = 0 を解く
% (3) FA(x,y,z)=0 かつ FB(x,y,z)=0 を解く(交面,交線,交点を求める)
% ansz : algsys([FA,FB],[z])
% [ansy,fy] : elimalg1([FA,FB],z,y)
% fy : eliminate([FA,FB],[z])
% ansy : algsys([fy],[y])
% [ansx,fx] : elimalg1(fy,y,x)
% fx : eliminate([fy,diff(fy,y)],[y])
% ansx : algsys([fx],[x])4 適用例
4.1 多重積分への応用
2重積分 \(\displaystyle \int\!\!\int_D\, (x+y+5)\,dx\,dy,~~ D =\{(x,y):~ 1 \leq x^2+y^2 < 9\}\) を求める(実行例8参照).
実行例 8
(%i2) display2d : false$
(%i3) D:on3ineq([x^2+y^2,1,9,co]); <-- 定義域Dの定義
(%o3) on3(x,1,3,co)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo)
+on3(x,-3,-1,oc)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo)
+on3(x,-1,1,oo)*on3(y,-sqrt(9-x^2),-sqrt(1-x^2),oc)
+on3(x,-1,1,oo)*on3(y,sqrt(1-x^2),sqrt(9-x^2),co)
(%i4) fxy:(x+y+5)*D; <-- 被積分関数の定義
(%o4) (y+x+5)*(on3(x,1,3,co)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo)
+on3(x,-3,-1,oc)*on3(y,-sqrt(9-x^2),sqrt(9-x^2),oo)
+on3(x,-1,1,oo)*on3(y,-sqrt(9-x^2),-sqrt(1-x^2),oc)
+on3(x,-1,1,oo)*on3(y,sqrt(1-x^2),sqrt(9-x^2),co))
(%i5) fx:on3integ10(fxy,y); <-- 変数yに関する定積分
(%o5) 2*x*sqrt(9-x^2)*on3(x,1,3,co)+10*sqrt(9-x^2)*on3(x,1,3,co)
+((9-x^2)/2-(1-x^2)/2)*on3(x,-1,1,oo)+((1-x^2)/2-(9-x^2)/2)*on3(x,-1,1,oo)
+2*(x*sqrt(9-x^2)-x*sqrt(1-x^2))*on3(x,-1,1,oo)
+2*(5*sqrt(9-x^2)-5*sqrt(1-x^2))*on3(x,-1,1,oo)
+2*x*sqrt(9-x^2)*on3(x,-3,-1,oc)+10*sqrt(9-x^2)*on3(x,-3,-1,oc)
(%i6) f:on3integ10(fx,x); <-- 変数xに関する定積分
(%o6) 40*%pi <-- 結果- Maxima 実行例 8
display2d : false$
D:on3ineq([x^2+y^2,1,9,co],'noplot,'noview); /* <-- 定義域Dの定義 */
fxy:(x+y+5)*D; /* <-- 被積分関数の定義 */
fx:on3integ19(fxy,y,minf,inf); /* <-- 変数yに関する定積分 */
f:on3integ19(fx,x,minf,inf); /* <-- 変数xに関する定積分 */## ~/bin/go TMP/tmp_lang/chunk-9.mxl > TMP/tmp_lang/chunk-9.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-9.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-9.mxl
## display2d:false
## D:on3ineq([x^2+y^2,1,9,co],'noplot,'noview)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## fxy:(x+y+5)*D
## D*(y+x+5)
## fx:on3integ19(fxy,y,minf,inf)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## f:on3integ19(fx,x,minf,inf)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-9.mxl"なお,関数on3integ10() は on3 関数を伴った式の積分関数である(井上(2008)参照).
4.1 統計への使用例1
平均ベクトル\((0,\,0)\),分散ベクトル\((1,\,1)\),相関係数\(0.7\)をもつ2変量正規分布の同時確率密度関数を \(\phi(x,\,y)\)とする.この確率分布において,定義域を \(D_0 = \{(x,\,y):\,-4 \leq x \leq 4,~ -4 \leq y \leq 4\}\)に制限した打ち切り正規分布を考えるとその確率密度関数\(f(x,\,y)\)は \[ f(x,\,y) = \frac{\phi(x,\,y)} { \int\!\!\int_{D_0}\, \phi(x,\,y)\,dx\,dy}, \quad (x,\,y) \in D_0 \] で与えられる.ここで,領域 \(D\) を \[ D = \{(x,\,y):\, x+y \geq 2, ~ x \leq 1 \} \] として,確率\(P\{(X,\,Y) \in D\}\) を求める問題を考える. この問題は,2段階選抜試験において1次試験の得点を\(x\),2次試験の得点を\(y\)とするとき,\(x+y \geq 2\)を合格とすべきを,1次選抜で \(x < 1\)で足切りを行った為に不合格となった確率を求める問題を模擬している. 以下に実行結果を実行例9および図6に示す.
実行例 9
(%i2) D0:on3ineq([[x,-4,4,cc],[y,-4,4,cc]]); <- 制限領域の設定
(%o2) on3(x,-4,4,cc)*on3(y,-4,4,cc)
(%i3) f:nor2d(x,y,0,0,1,1,0.7); <- 平均(0,0),分散(1,1),相関係数0.7の正規分布の確率密度関数
(%o3) 0.70014*%e^-(0.980392*(y^2-1.4*x*y+x^2))/%pi
(%i4) Fxy0:expand(f*D0); <- 制限領域D0上の確率密度関数
(%o4) 0.70014*on3(x,-4,4,cc)*%e^(-0.980392*y^2+1.372549*x*y-0.980392*x^2)*on3(y,-4,4,cc)/%pi
(%i5) Fx0:on3integ10(Fxy0,y);
(%o5) on3(x,-4,4,cc)
*(0.140028*sqrt(51)*%e^-(x^2/2)
*erf(7*x/(sqrt(2)*sqrt(51))+5*2^(5/2)/sqrt(51))/(2^(3/2)*sqrt(%pi))
-0.140028*sqrt(51)*%e^-(x^2/2)
*erf(7*x/(sqrt(2)*sqrt(51))-5*2^(5/2)/sqrt(51))/(2^(3/2)*sqrt(%pi)))
(%i6) F0:on3romberg(Fx0);
(%o6) 0.999878
(%i7) fdens:f/F0; <- D0上の同時確率密度関数
(%o7) 0.700225*%e^-(0.980392*(y^2-1.4*x*y+x^2))/%pi
(%i8) D:on3ineq([[x+y,2,inf,co],[x,-4,1,cc],[y,-4,4,cc]]); <- 着目領域Dの設定
(%o8) on3(x,-2,1,cc)*on3(y,2-x,4,cc)
(%i9) Fxy:expand(fdens*D); <- D上の同時確率密度関数
(%o9) 0.700225*on3(x,-2,1,cc)*%e^(-0.980392*y^2+1.372549*x*y-0.980392*x^2)*on3(y,2-x,4,cc)/%pi
(%i10) Fx:on3integ10(Fxy,y); <- yで積分しxの周辺確率密度関数を得る
(%o10) on3(x,-2,1,cc)
*(0.140028*sqrt(51)*%e^-(x^2/2)
*erf(7*x/(sqrt(2)*sqrt(51))-5*sqrt(2)*(2-x)/sqrt(51))/(2^(3/2)*sqrt(%pi))
-0.140028*sqrt(51)*%e^-(x^2/2)
*erf(7*x/(sqrt(2)*sqrt(51))-5*2^(5/2)/sqrt(51))/(2^(3/2)*sqrt(%pi)))
(%i11) P:on3romberg(Fx); <- ロンバーグ積分によりxで積分する
(%o11) 0.027529 <- 結果の確率値
\includegraphics[width=24em,height=17em]{./q3-1.eps}
\includegraphics[width=24em,height=17em]{./q3-3.eps}
\caption{2変量正規分布{\sc \footnotesize (左図)}と定義域$D$上の正規分布{\sc \footnotesize (右図)}}- Maxima 実行例 9
q3('go, 'file_name="figs/q3", 'columns=2, 'dimensions=[1000,500], 'noview);## ~/bin/go TMP/tmp_lang/chunk-10.mxl > TMP/tmp_lang/chunk-10.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-10.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-10.mxl
## q3('go,'file_name = "figs/q3",'columns = 2,'dimensions = [1000,500],'noview)
## CS: progn = <q3> , dlist =
## [terminal = png,file_name = "figs/q3",columns = 2,dimensions = [1000,500]]
## ★
## ( /* 領域D0の設定, 相関のある2変量標準正規分布の確率密度関数 f の設定 */
##
## D0:on3ineq([[x,-4,4,cc],[y,-4,4,cc]],'resultonly,'noview),
##
## f:nor2d(x,y, 0,0, 1,1, 0.7), /* 相関のある2変量標準正規分布の確率密度関数 */
##
## Fxy0:expand(f*D0), Fx0:on3integ19(Fxy0,y,minf,inf), F0:on3romberg(Fx0),cshow(F0)
## )
## Condition in MEVAL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## CS: == Error in backsolve ==
## Maxima encountered a Lisp error:
## Condition in MEVAL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-10.mxl"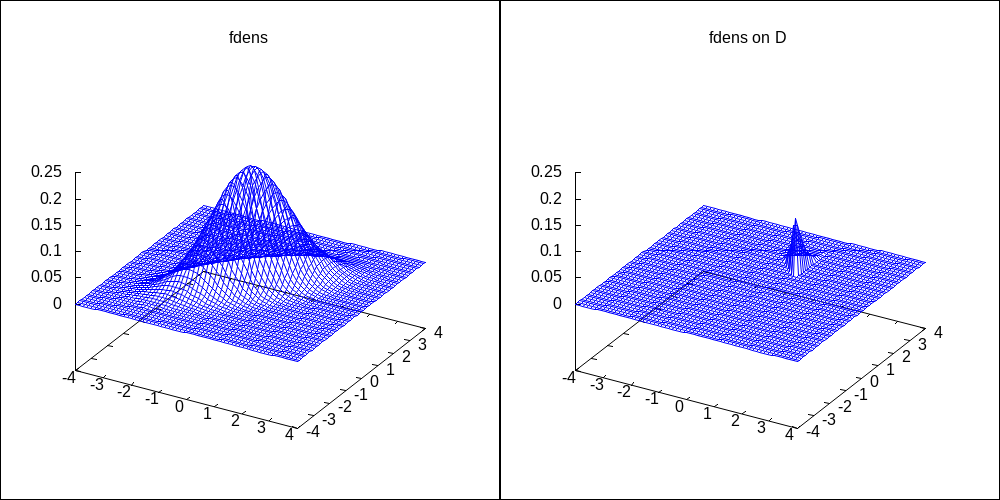
実行例9に現れる関数\({\rm erf(x)}\)は\({\rm Maxima}\)の標準関数で誤差関数と呼ばれている.ただし,標準正規分布の分布関数\(\Phi(z)\)との関係は \[ \Phi(z)=({\rm erf}(x)+1)/2,~~ z=x/\sqrt{2} \] であることに注意する.また,\({\rm on3romberg()}\)は\({\rm on3}\)関数を伴った式のロンバーグ積分である.
4.3 統計への使用例2
確率変数\(X\)と\(Y\)が互いに独立に標準正規分布に従い,領域\(D\)が \(D = \{(x,y)\,:\, 1 \leq x^3+x\,y+y^2 < 9 ~かつ~ -4 \leq y < 4 \}\) で表せるとき, 確率\(P\{(X,\,Y) \in D\}\)を求める問題を考える.結果を実行例10および図7に示す.
実行例 10
(%i1) D:on3ineq([[x^3+x*y+y^2,1,9,co],[y,-4,4,co]]); <- 領域Dの陽関数表現を得る
(%o1) on3(x,1.0906606,2.1668449,co)*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,
(sqrt(-4*x^3+x^2+36)-x)/2,oo)
+on3(x,-1.2553831,1.0906606,oo)*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,
-(sqrt(-4*x^3+x^2+4)+x)/2,oc)
+on3(x,-1.9359795,-1.2553831,oc)*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,
-(sqrt(-4*x^3+x^2+4)+x)/2,oc)
+on3(x,-2.5891325,-1.9359795,cc)*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,
-(sqrt(-4*x^3+x^2+4)+x)/2,oc)
+on3(x,-1.2553831,1.0906606,oo)*on3(y,(sqrt(-4*x^3+x^2+4)-x)/2,
(sqrt(-4*x^3+x^2+36)-x)/2,co)
+on3(x,-1.9359795,-1.2553831,oc)*on3(y,(sqrt(-4*x^3+x^2+4)-x)/2,4,co)
+on3(x,-3,-2.5891325,co)*on3(y,-4,-(sqrt(-4*x^3+x^2+4)+x)/2,cc)
(%i2) f:exp((-(x^2+y^2))/2)/(2*%pi); <- 2変量正規分布の確率密度関数
(%o2) %e^((-y^2-x^2)/2)/(2*%pi)
(%i3) Fxy:expand(f*D); <- 定義域D上の同時密度関数
(%o3) on3(x,1.0906606,2.1668449,co)*%e^(-y^2/2-x^2/2)
*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,(sqrt(-4*x^3+x^2+36)-x)/2,oo)/(2*%pi)
+on3(x,-1.2553831,1.0906606,oo)*%e^(-y^2/2-x^2/2)
*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,-(sqrt(-4*x^3+x^2+4)+x)/2,oc)/(2*%pi)
+on3(x,-1.9359795,-1.2553831,oc)*%e^(-y^2/2-x^2/2)
*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,-(sqrt(-4*x^3+x^2+4)+x)/2,oc)/(2*%pi)
+on3(x,-2.5891325,-1.9359795,cc)*%e^(-y^2/2-x^2/2)
*on3(y,-(sqrt(-4*x^3+x^2+36)+x)/2,-(sqrt(-4*x^3+x^2+4)+x)/2,oc)/(2*%pi)
+on3(x,-1.2553831,1.0906606,oo)*%e^(-y^2/2-x^2/2)
*on3(y,(sqrt(-4*x^3+x^2+4)-x)/2,(sqrt(-4*x^3+x^2+36)-x)/2,co)/(2*%pi)
+on3(x,-1.9359795,-1.2553831,oc)*%e^(-y^2/2-x^2/2)
*on3(y,(sqrt(-4*x^3+x^2+4)-x)/2,4,co)/(2*%pi)
+on3(x,-3,-2.5891325,co)*%e^(-y^2/2-x^2/2)
*on3(y,-4,-(sqrt(-4*x^3+x^2+4)+x)/2,cc)/(2*%pi)
(%i4) Fx:on3integ10(Fxy,y); <- xの周辺密度関数
(%o4) on3(x,1.0906606,2.1668449,co)
*(%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi))
+%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)-x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-1.2553831,1.0906606,oo)
*(%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-1.9359795,-1.2553831,oc)
*(%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-2.5891325,-1.9359795,cc)
*(%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-1.2553831,1.0906606,oo)
*(%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+36)-x)/2^(3/2))/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)-x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-3,-2.5891325,co)
*(erf(2^(3/2))*%e^-(x^2/2)/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)+x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
+on3(x,-1.9359795,-1.2553831,oc)
*(erf(2^(3/2))*%e^-(x^2/2)/(2^(3/2)*sqrt(%pi))
-%e^-(x^2/2)*erf((sqrt(-4*x^3+x^2+4)-x)/2^(3/2))/(2^(3/2)*sqrt(%pi)))
(%i5) P:on3romberg(Fx); <- 結果の確率値
(%o5) 0.363095
\caption{定義域$D$の領域{\sc \footnotesize (左図)}と$D$上の正規分布{\sc \footnotesize (右図)}}- Maxima 実行例 10
q4('go, 'file_name="figs/q4", 'columns=2, 'dimensions=[1000,500], 'noview);## ~/bin/go TMP/tmp_lang/chunk-11.mxl > TMP/tmp_lang/chunk-11.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-11.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-11.mxl
## q4('go,'file_name = "figs/q4",'columns = 2,'dimensions = [1000,500],'noview)
## ★ ( /* 定義域 D 上の関数 f=f(x,Y) の積分 */
## D:on3ineq([[x^3+x*y+y^2,1,9,co],[y,-4,4,co]],'resultonly,'noplot,'noview),
## print("D = ",D),
## f0:exp(-(x^2+y^2)/2)/(2*%pi), Fxy:expand(f0 * D),
## print("Fxy=",Fxy),
## Fx:on3integ19(Fxy,y,minf,inf),
## print("Fx=",Fx),
## P:on3romberg(expand(Fx)),
## print("P=",P) )
## Maxima encountered a Lisp error:
## Condition in MEVAL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-11.mxl"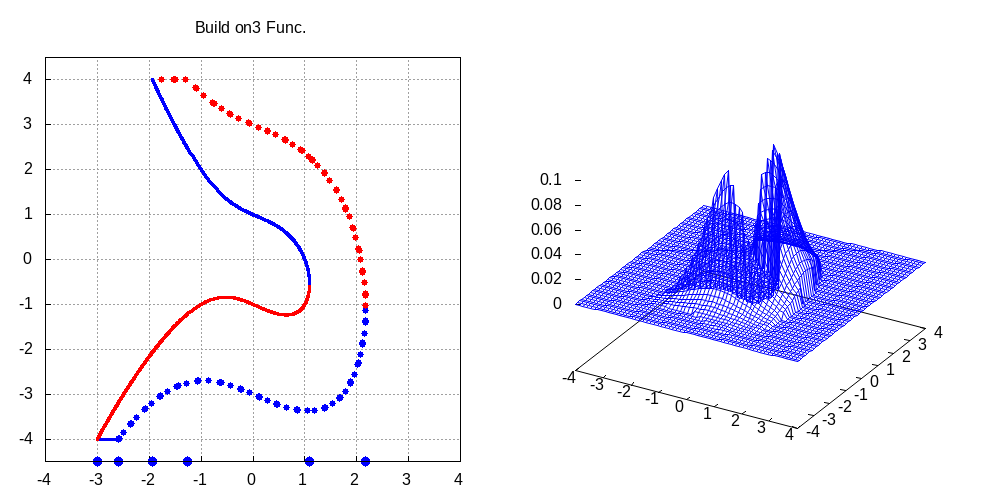
5 ライブラリの公開
本稿に示した関数 on3ineq() を公開します.必要な方は筆者連絡先にメールを下さい. 但し,開発途上である点をご承知下さい.また,ご批判,コメントは歓迎します.
謝辞
Maxima の開発者,メンテナー,ドキュメント作成者,それを日本語に訳された方々,等に感謝する. また,2人の審査員からは有益な助言を頂いた.深く感謝する.
\begin{thebibliography}{99}
%\bibitem{Okumura}
%奥村晴彦 (2000):
%[改訂版]\LaTeXe\ 美文書作成入門,
%技術評論社,東京.
\bibitem{MacsymaBook}
Barbara Heller (1991): {\it Macsyma for statisticians}, John Wiley, New York.
\bibitem{Macsyma}
Macsyma 対訳レファレンスマニュアル(数学/システム)16版 (1996),スリースカンパニー,
東京.
\bibitem{1}Maxima Reference Manual Version 5.11.0 (2006).
\bibitem{Inoue}
井上隆勝 (2008):
定義域を伴った関数の数式処理,
応用統計学~ 37巻1号.
\bibitem{Saito}
近藤祐史,齋藤友克 (2005):
数式処理における関数零点の描画,
数式処理~ 12巻1号.
\bibitem{Saito}
齋藤友克,竹島卓,平野照比古 (2003):
グレブナー基底の計算 実践篇 Risa/Asir で解く,
東京大学出版会.
\bibitem{Nakagawa}
中川義行 (2005):
Maxima 入門ノート 1.2.1
\bibitem{Saito}
野呂正行,横山和弘 (2003):
グレブナー基底の計算 基礎篇 計算代数入門,
東京大学出版会.
\bibitem{Yokota-1}横田博史 (2002): Maxima Manual(日本語訳版).
\bibitem{Yokota-2}
横田博史 (2006):
はじめてのMaxima,工学社,東京.
\bibitem{Yokota-3}横田博史 (2007): Maxima簡易マニュアル.
\bibitem{Maxima}
Maxima 公式サイト : http://maxima.sourceforge.net.
\end{thebibliography}%% 英語抄録
\LastPageinEnglish
\title{An Attempt at a Solution of a Multivariate Inequality on a Formula Processing Language}
% A trial to the symbolic elucidation of the inequality about a multinomial expression}
%\subtitle{}
\authorlist{%
\authorentry{Takakatsu Inoue}{NU}
% \authorentry*{}{}
}
\affiliate[NU]{College of Industrial Technology, Nihon University}
%\breakauthorline{1,2}
\maketitle
\begin{abstract}
% It deals with a problem to solve an inequality about a multinomial expression in
% the symbolic mathematical manipulation software, Maxima. It is expanded in the case of an
% inequality about the rational expression to have a multinomial expression to a numerator and/or
% a denominator and also the case of a coalition inequality. A tool for doing
% algebraic operation is provided as a function of Maxima.
A problem of solving an inequality involving a multivariate function is taken up.
A multivariate function is assumed to be in the form of a multivariate polynomial or rational formula having a multivariate polynomial as its numerator and denominator.
Simultaneous inequalities are also covered.
A procedure for solving such an inequality is shown and compiled as the function on3ineq( ) on the formula processing language Maxima.
An example is shown for using it to verify its function.
\end{abstract}
\begin{keywords}
multinomial inequality, symbolic manipulation, Maxima
\end{keywords}
% 2-11-1 Shin'ei, Narashino 275-0005 Japan
\CorrespondingAuthor{
inoue.takakatsu@nihon-u.ac.jp
}
\refereed
\end{langument}