w2018.Rmd Memo
INOUE Takakatsu 更新:2024-05-21
逆行列
hilbert <- function(n) { i <- 1:n; 1 / outer(i - 1, i, "+") } # ヒルベルト行列
h5 <- hilbert(5); h5 # 5x5 のヒルベルト行列 h5 を作成## [,1] [,2] [,3] [,4] [,5]
## [1,] 1.0000000 0.5000000 0.3333333 0.2500000 0.2000000
## [2,] 0.5000000 0.3333333 0.2500000 0.2000000 0.1666667
## [3,] 0.3333333 0.2500000 0.2000000 0.1666667 0.1428571
## [4,] 0.2500000 0.2000000 0.1666667 0.1428571 0.1250000
## [5,] 0.2000000 0.1666667 0.1428571 0.1250000 0.1111111sh5 <- solve(h5); sh5 # h5 の逆行列 sh5 を求める## [,1] [,2] [,3] [,4] [,5]
## [1,] 25 -300 1050 -1400 630
## [2,] -300 4800 -18900 26880 -12600
## [3,] 1050 -18900 79380 -117600 56700
## [4,] -1400 26880 -117600 179200 -88200
## [5,] 630 -12600 56700 -88200 44100round(sh5 %*% h5, 7) # 有効桁数を7とした表示## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 0 0 0 0
## [2,] 0 1 0 0 0
## [3,] 0 0 1 0 0
## [4,] 0 0 0 1 0
## [5,] 0 0 0 0 1svd(h5)$d## [1] 1.567051e+00 2.085342e-01 1.140749e-02 3.058980e-04 3.287929e-06eigen(h5)$values # ## [1] 1.567051e+00 2.085342e-01 1.140749e-02 3.058980e-04 3.287929e-06eigen(hilbert(15))$values## [1] 1.845928e+00 4.266280e-01 5.721209e-02 5.639835e-03 4.364766e-04
## [6] 2.710854e-05 1.361582e-06 5.528988e-08 1.802960e-09 4.657787e-11
## [11] 9.321559e-13 1.394656e-14 1.436092e-16 -6.578228e-19 -2.694225e-18out <- try(solve(hilbert(15)),TRUE)
print(out)## [1] "Error in solve.default(hilbert(15)) : \n system is computationally singular: reciprocal condition number = 1.5434e-18\n"
## attr(,"class")
## [1] "try-error"
## attr(,"condition")
## <simpleError in solve.default(hilbert(15)): system is computationally singular: reciprocal condition number = 1.5434e-18>ヒルベルト(部分)行列の特異値分解
hilbert <- function(n) { i <- 1:n; 1 / outer(i - 1, i, "+") } # ヒルベルト行列
X <- hilbert(9)[, 1:6] # 9x6 行列 X を作成
(s <- svd(X))## $d
## [1] 1.668433e+00 2.773727e-01 2.223722e-02 1.084693e-03 3.243788e-05
## [6] 5.234864e-07
##
## $u
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -0.7244999 0.6265620 0.27350003 -0.08526902 0.02074121 -0.00402455
## [2,] -0.4281556 -0.1298781 -0.64293597 0.55047428 -0.27253421 0.09281592
## [3,] -0.3121985 -0.2803679 -0.33633240 -0.31418014 0.61632113 -0.44090375
## [4,] -0.2478932 -0.3141885 -0.06931246 -0.44667149 0.02945426 0.53011986
## [5,] -0.2063780 -0.3140734 0.10786005 -0.30241655 -0.35566839 0.23703838
## [6,] -0.1771408 -0.3026808 0.22105904 -0.09041508 -0.38878613 -0.26044927
## [7,] -0.1553452 -0.2877310 0.29280775 0.11551327 -0.19285565 -0.42094482
## [8,] -0.1384280 -0.2721599 0.33783778 0.29312535 0.11633231 -0.16079025
## [9,] -0.1248940 -0.2571250 0.36542543 0.43884649 0.46496714 0.43459954
##
## $v
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -0.7364928 0.6225002 0.2550021 -0.06976287 0.01328234 -0.001588146
## [2,] -0.4432826 -0.1818705 -0.6866860 0.50860089 -0.19626669 0.041116974
## [3,] -0.3274789 -0.3508553 -0.2611139 -0.50473697 0.61605641 -0.259215626
## [4,] -0.2626469 -0.3921783 0.1043599 -0.43747940 -0.40833605 0.638901622
## [5,] -0.2204199 -0.3945644 0.3509658 0.01612426 -0.46427916 -0.675826789
## [6,] -0.1904420 -0.3831871 0.5110654 0.53856351 0.44663632 0.257248908 D <- diag(s$d)
s$u %*% D %*% t(s$v) # X = U D V'## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1.0000000 0.5000000 0.33333333 0.25000000 0.20000000 0.16666667
## [2,] 0.5000000 0.3333333 0.25000000 0.20000000 0.16666667 0.14285714
## [3,] 0.3333333 0.2500000 0.20000000 0.16666667 0.14285714 0.12500000
## [4,] 0.2500000 0.2000000 0.16666667 0.14285714 0.12500000 0.11111111
## [5,] 0.2000000 0.1666667 0.14285714 0.12500000 0.11111111 0.10000000
## [6,] 0.1666667 0.1428571 0.12500000 0.11111111 0.10000000 0.09090909
## [7,] 0.1428571 0.1250000 0.11111111 0.10000000 0.09090909 0.08333333
## [8,] 0.1250000 0.1111111 0.10000000 0.09090909 0.08333333 0.07692308
## [9,] 0.1111111 0.1000000 0.09090909 0.08333333 0.07692308 0.07142857 t(s$u) %*% X %*% s$v # D = U' X V## [,1] [,2] [,3] [,4] [,5]
## [1,] 1.668433e+00 4.163336e-17 1.665335e-16 -2.775558e-16 8.326673e-17
## [2,] 1.214306e-16 2.773727e-01 0.000000e+00 2.775558e-17 2.775558e-17
## [3,] 7.762888e-17 -4.336809e-17 2.223722e-02 1.734723e-17 -1.301043e-17
## [4,] -7.956689e-17 3.699840e-17 -6.722053e-18 1.084693e-03 -2.981556e-18
## [5,] 3.843116e-17 3.057111e-17 1.626727e-17 3.926845e-18 3.243788e-05
## [6,] 3.097149e-17 5.394012e-19 -1.123645e-17 -6.214403e-18 1.613745e-17
## [,6]
## [1,] -9.714451e-17
## [2,] 3.469447e-17
## [3,] 1.170938e-17
## [4,] -1.910906e-17
## [5,] -2.688483e-18
## [6,] 5.234864e-07固有値分解
### 1. 実非対称行列の固有値分解;
A <- matrix(c(1, 0.5, 0.25, 0.75), ncol=2, byrow=T); A;## [,1] [,2]
## [1,] 1.00 0.50
## [2,] 0.25 0.75ans <- eigen(A); ans;## eigen() decomposition
## $values
## [1] 1.25 0.50
##
## $vectors
## [,1] [,2]
## [1,] 0.8944272 -0.7071068
## [2,] 0.4472136 0.7071068G <- ans$vectors; G;## [,1] [,2]
## [1,] 0.8944272 -0.7071068
## [2,] 0.4472136 0.7071068D <- diag(ans$values); D;## [,1] [,2]
## [1,] 1.25 0.0
## [2,] 0.00 0.5B <- G %*% D %*% solve(G)
B;## [,1] [,2]
## [1,] 1.00 0.50
## [2,] 0.25 0.75### 2. 実対称行列の固有値分解;
A <- matrix(c(1, 0.5, 0.5, 1), ncol=2, byrow=T); A;## [,1] [,2]
## [1,] 1.0 0.5
## [2,] 0.5 1.0ans <- eigen(A); ans;## eigen() decomposition
## $values
## [1] 1.5 0.5
##
## $vectors
## [,1] [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068 0.7071068G <- ans$vectors; G;## [,1] [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068 0.7071068D <- diag(ans$values); D;## [,1] [,2]
## [1,] 1.5 0.0
## [2,] 0.0 0.5B <- G %*% D %*% solve(G)
B;## [,1] [,2]
## [1,] 1.0 0.5
## [2,] 0.5 1.0### 3. 実対称行列(ランク落ち)の固有値分解;
A <- matrix(c(1, 1, 1, 1), ncol=2, byrow=T); A;## [,1] [,2]
## [1,] 1 1
## [2,] 1 1ans <- eigen(A); ans;## eigen() decomposition
## $values
## [1] 2 0
##
## $vectors
## [,1] [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068 0.7071068G <- ans$vectors; G;## [,1] [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068 0.7071068D <- diag(ans$values); D;## [,1] [,2]
## [1,] 2 0
## [2,] 0 0B <- G %*% D %*% solve(G)
B;## [,1] [,2]
## [1,] 1 1
## [2,] 1 1### 4. 実対称行列(自明)の固有値分解;
A <- matrix(c(2, 0, 0, 2), ncol=2, byrow=T); A;## [,1] [,2]
## [1,] 2 0
## [2,] 0 2ans <- eigen(A); ans;## eigen() decomposition
## $values
## [1] 2 2
##
## $vectors
## [,1] [,2]
## [1,] 0 -1
## [2,] 1 0G <- ans$vectors; G;## [,1] [,2]
## [1,] 0 -1
## [2,] 1 0D <- diag(ans$values); D;## [,1] [,2]
## [1,] 2 0
## [2,] 0 2B <- G %*% D %*% solve(G)
B;## [,1] [,2]
## [1,] 2 0
## [2,] 0 2特異値分解
### 1. 実行列の特異値分解 A = U D V' ;
p <- 3;
A <- matrix(c(1, 1, 0,
1, 1, 0,
1, 0, 1,
1, 0, 1), ncol=p, byrow=T); A;## [,1] [,2] [,3]
## [1,] 1 1 0
## [2,] 1 1 0
## [3,] 1 0 1
## [4,] 1 0 1ans <- svd(A); ans;## $d
## [1] 2.449490e+00 1.414214e+00 8.546501e-17
##
## $u
## [,1] [,2] [,3]
## [1,] -0.5 -0.5 7.071068e-01
## [2,] -0.5 -0.5 -7.071068e-01
## [3,] -0.5 0.5 0.000000e+00
## [4,] -0.5 0.5 1.110223e-16
##
## $v
## [,1] [,2] [,3]
## [1,] -0.8164966 -1.541976e-16 0.5773503
## [2,] -0.4082483 -7.071068e-01 -0.5773503
## [3,] -0.4082483 7.071068e-01 -0.5773503ev <- ans$d;
for (i in p:1) {if (abs(ev[i]) < 1.0e-15) rnk <- i-1};
rnk; ## [1] 2### rank まで再計算する;
ans <- svd(A,nu=rnk,nv=rnk); ans;## $d
## [1] 2.449490e+00 1.414214e+00 8.546501e-17
##
## $u
## [,1] [,2]
## [1,] -0.5 -0.5
## [2,] -0.5 -0.5
## [3,] -0.5 0.5
## [4,] -0.5 0.5
##
## $v
## [,1] [,2]
## [1,] -0.8164966 -1.541976e-16
## [2,] -0.4082483 -7.071068e-01
## [3,] -0.4082483 7.071068e-01U <- ans$u; U;## [,1] [,2]
## [1,] -0.5 -0.5
## [2,] -0.5 -0.5
## [3,] -0.5 0.5
## [4,] -0.5 0.5ans$d;## [1] 2.449490e+00 1.414214e+00 8.546501e-17ans$d[1:rnk];## [1] 2.449490 1.414214D <- diag(ans$d[1:rnk]); D;## [,1] [,2]
## [1,] 2.44949 0.000000
## [2,] 0.00000 1.414214V <- ans$v
B <- U %*% D %*% t(V)
B;## [,1] [,2] [,3]
## [1,] 1 1.000000e+00 -1.665335e-16
## [2,] 1 1.000000e+00 -1.665335e-16
## [3,] 1 5.551115e-17 1.000000e+00
## [4,] 1 5.551115e-17 1.000000e+00### 2. A'A の固有値分解 A'A = V D^2 V' ;
ATA <- t(A) %*% A; ATA;## [,1] [,2] [,3]
## [1,] 4 2 2
## [2,] 2 2 0
## [3,] 2 0 2eigen(ATA);## eigen() decomposition
## $values
## [1] 6.000000e+00 2.000000e+00 3.552714e-15
##
## $vectors
## [,1] [,2] [,3]
## [1,] 0.8164966 0.0000000 0.5773503
## [2,] 0.4082483 -0.7071068 -0.5773503
## [3,] 0.4082483 0.7071068 -0.5773503### 3. 射影行列 Q = U U';
Q <- U %*% t(U); Q;## [,1] [,2] [,3] [,4]
## [1,] 0.5 0.5 0.0 0.0
## [2,] 0.5 0.5 0.0 0.0
## [3,] 0.0 0.0 0.5 0.5
## [4,] 0.0 0.0 0.5 0.5乱数
一様乱数
if (1) {
# postscript("Rfig-1a.eps",height=18,horizontal=F)
# par(mfrow=c(2,1),cex.main=1.5,cex.axis=1.5,lwd=1.5)
nc <- c(100,10000)
for (i in 1:length(nc)) {
set.seed(1)
n <- nc[i]
x <- runif(n)
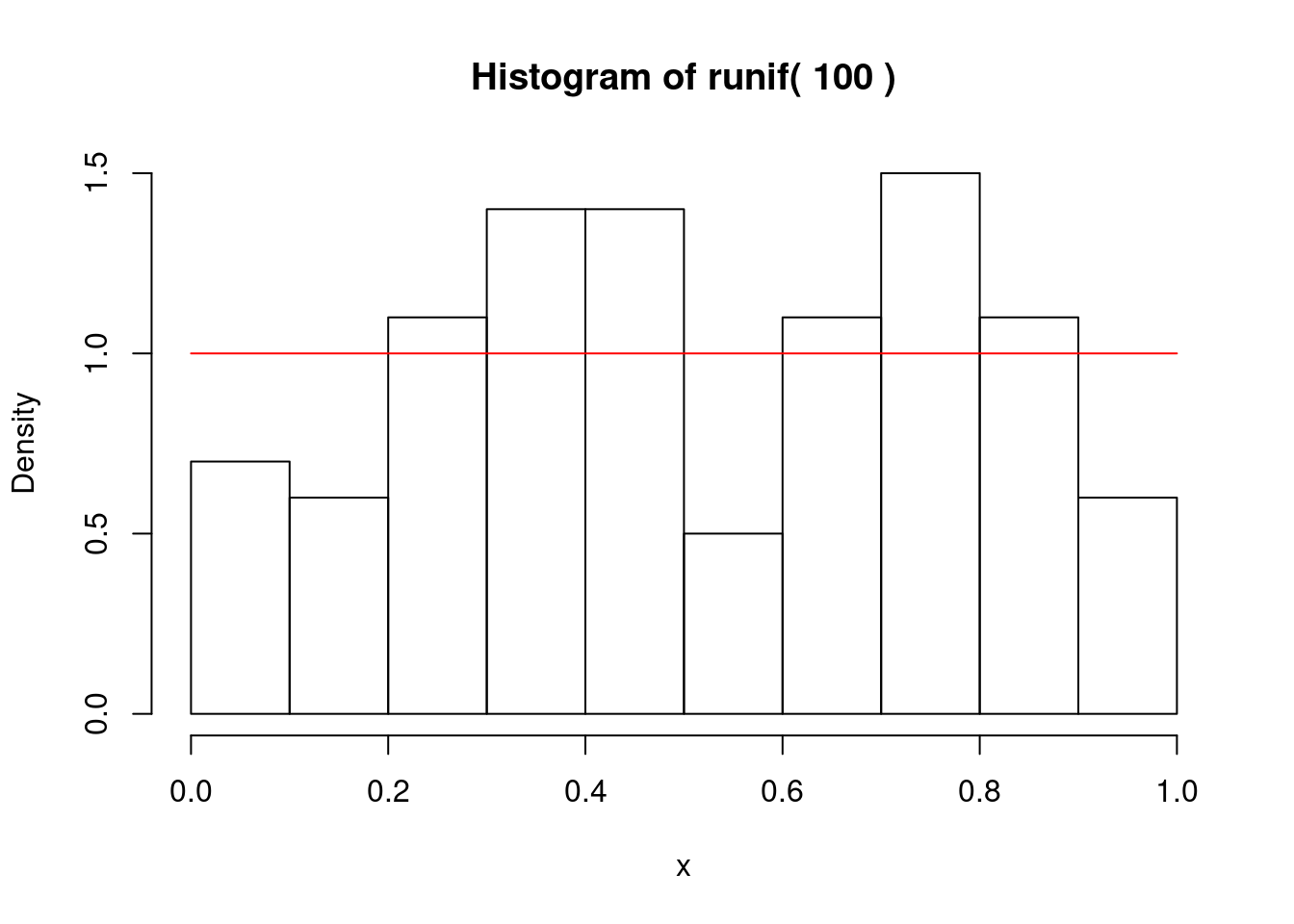
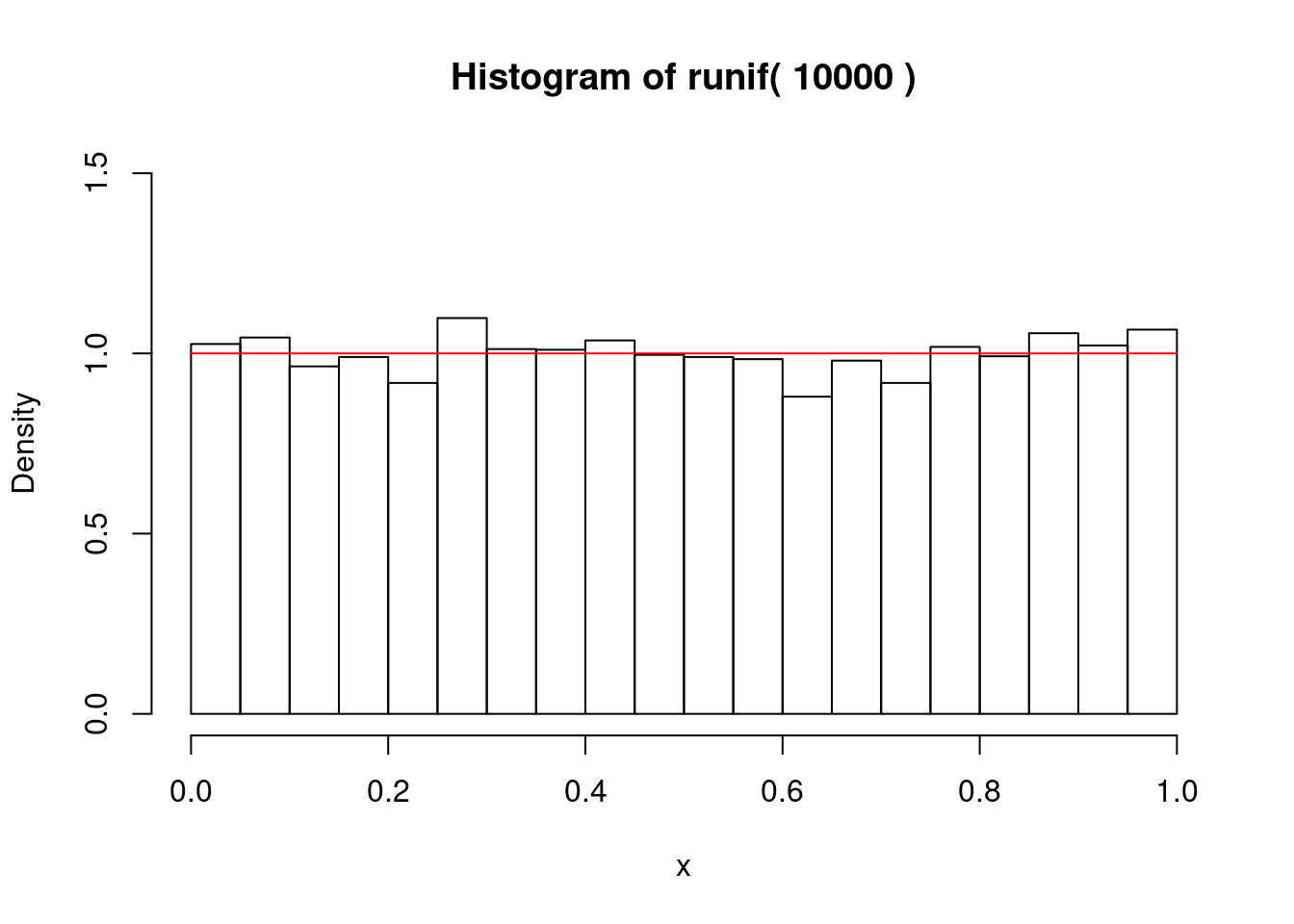
gmain <- paste("Histogram of runif(",n,")")
hist(x,freq=F,main=gmain,xlim=c(0,1),ylim=c(0,1.5))
curve(dunif,0,1,add=T,col="red")
}
# graphics.off()
}
指数乱数
確率密度関数\(f(x)\)が\[ f(x) = \lambda\, e^{- \lambda x} \quad (x \ge 0) \] で表せる確率分布を「母数\(\lambda\)の指数分布」といい,\(X \sim {\rm Ex} (\lambda)\) と記す.このとき,分布関数\(F(x) = P\{ X < x\}\)は\(F(x) = 1 - e^{-\lambda x}\) で表せる.\(\lambda=1\)のときの指数分布の密度関数と分布関数を以下に示す.
### 指数分布の密度関数と分布関数のグラフ
# postscript("Rfig-2a.eps",horizontal=F)
par(mfrow=c(1,2),cex=1.2,lwd=1.5)
f <- function(x){dexp(x,rate=1.0)} # 確率密度関数
curve(f,0,8,col="red",main="Density Func")
F <- function(x){pexp(x,rate=1.0)} # 分布関数
curve(F,0,8,col="red",main="Cumulative Density Func")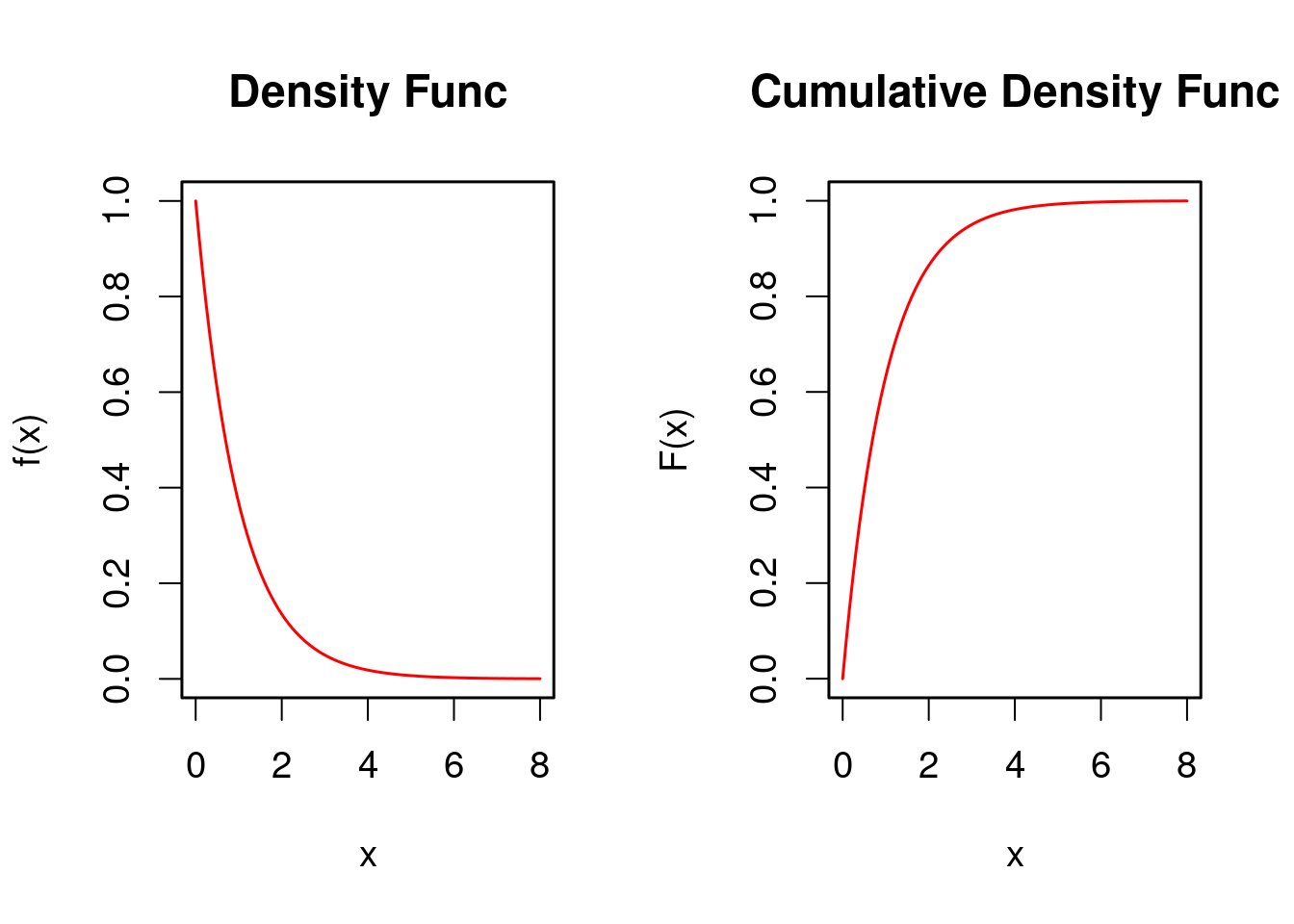
#graphics.off()
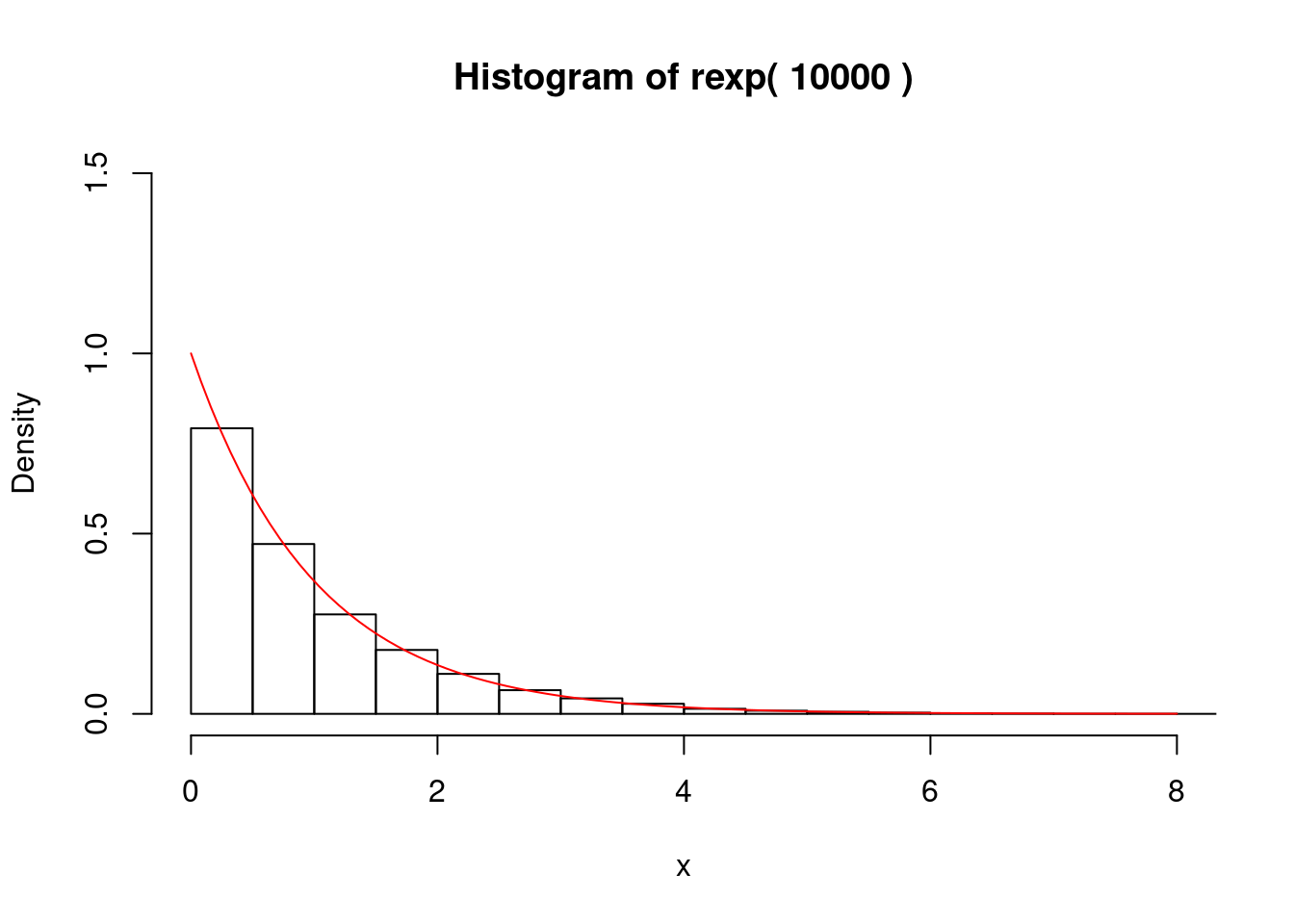
rm(f,F)分布関数のグラフ(右図)より,\(y=F(x)=1 - e^{- x}\)を\(x\)について解くと,\(x = - \log(1-y)\) を得る.よって,\(y\)を一様乱数とすると,\(x = - \log(1-y)\)で定まる\(x\)は指数分布に従う確率変数の 実現値,すなわち,指数乱数を得る.これを逆関数法による乱数変換という. 以下にRによる実行例を示す.
### 指数乱数 F(x) = 1 - e^(-x) = y : -x = log(1-y)
if (1) {
# postscript("Rfig-2.eps",height=6,horizontal=F);
# par(mfrow=c(1,1),cex.main=1.5,cex.axis=1.5,lwd=1.5)
set.seed(1)
n <- 10000
y <- runif(n)
x <- -log(1-y)
gmain <- paste("Histogram of rexp(",n,")")
hist(x,freq=F,main=gmain,xlim=c(0,8),ylim=c(0,1.5))
curve(dexp,0,8,add=T,col="red")
# graphics.off()
}
正規乱数
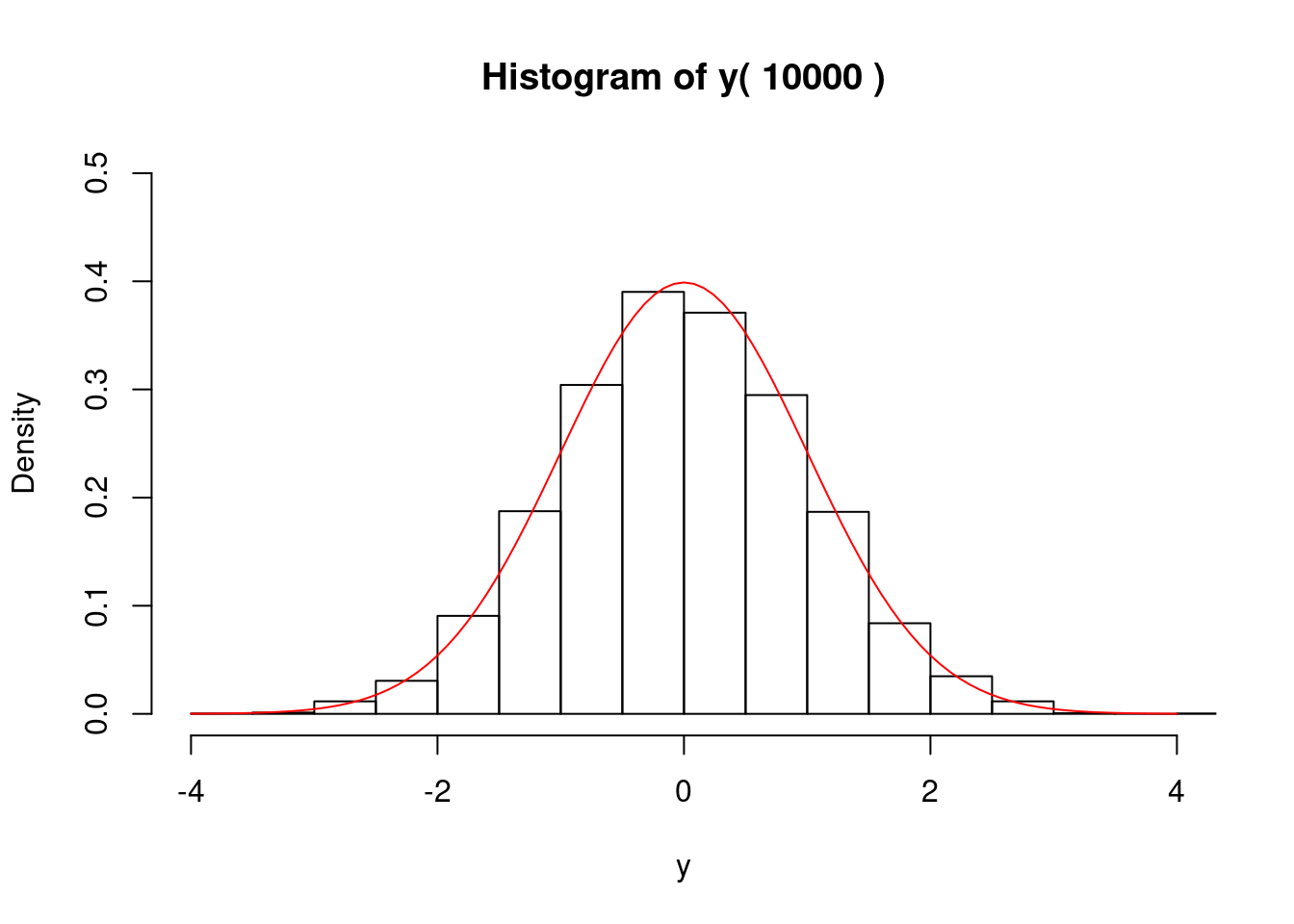
確率密度関数\(f(x)\)が\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\, e^{- \frac{(x-\mu)^2}{2\sigma^2}} \quad (-\infty < x < \infty) \] で表せる確率分布を「平均\(\mu\),分散\(\sigma^2\)の正規分布」といい,\(X \sim {\rm N} (\mu, \,\sigma^2)\) と記す.特に\(\mu=0,\,\sigma^2=1^2\)のときの正規分布\({\rm N} (0, \,1^2)\)を標準正規分布という. 以下では,標準正規分布に従う乱数(正規乱数)を中心刻限定理に基づいて生成する.
中心極限定理:
標本(確率変数)\(X_1,\cdots,X_s,\cdots,X_n\)が,互いに独立に同一の分布(平均\(\mu\),分散\(\sigma^2\))に従うとき 標本平均\(\bar{X} =
\frac{1}{n}\,\sum_{s=1}^{n}\,X_s\)は,標本数\(n\)の増加に伴い,正規分布 \({\rm N}(\mu,
\big(\frac{\sigma}{\sqrt{n}}\big)^2)\) に漸近する.
メモ: 総和\(T = \sum_{s=1}^{n}\,X_s\)は,正規分布 \({\rm N}(\mu, \big(\sqrt{n}\,\sigma \big)^2)\) に漸近する.また, 確率変数\(X\)が区間\([a,b)\)上の一様分布に従うとき,\(X\)の平均\(\mu\),分散\(\sigma^2\)はそれぞれ \(\mu = \frac{(a+b)}{2},~ \sigma^2 = \frac{(b-a)^2}{12}\)で表せる.
### 正規乱数
if (1) {
# postscript("Rfig-3.eps",height=6,horizontal=F);
# par(mfrow=c(1,1),cex.main=1.5,cex.axis=1.5,lwd=1.5)
set.seed(1)
n <- 10000; n0 <- n*12
x <- runif(n0,-0.5,0.5) # 区間[-0.5,0.5)上の一様乱数を生成
y <- rep(0,n)
for (i in 1:n) { # 12個づつの一様乱数の和を求める
js <- 12*(i-1)+1; je <- 12*i; y[i] <- sum(x[js:je])
}
gmain <- paste("Histogram of y(",n,")")
hist(y,freq=F,main=gmain,xlim=c(-4,4),ylim=c(0,0.5))
curve(dnorm,-4,4,add=T,col="red")
# graphics.off()
}
乱数の応用
### 円の面積:モンテカルロ積分
if (1) {
# postscript("Rfig-4.eps",height=9,horizontal=F);
# par(mfrow=c(1,1),pty="s",cex.main=1.5,cex.axis=1.5,lwd=1.5)
par(pty="s")
set.seed(1); n <- 1000; x <- runif(n); y <- runif(n)
ic <- 0; xin <- c(); yin <- c(); xout <- c(); yout <- c()
for (i in 1:n) {
if (x[i]^2+y[i]^2 <= 1)
{ ic <- ic + 1; xin <- c(xin,x[i]); yin <- c(yin,y[i]) }
else { xout <- c(xout,x[i]); yout <- c(yout,y[i]) }
} # end of for-i
estpi <- ic/n * 4
gmain <- paste("scatter plot of (x,y) n=",n," estpi=",estpi)
plot(xout,yout,main=gmain,xlim=c(-0.2,1.2),ylim=c(-0.2,1.2))
points(xin,yin,col="blue")
curve(sqrt(1-x^2),0,1,add=T,col="red")
grid(12,12)
# graphics.off()
} # end of if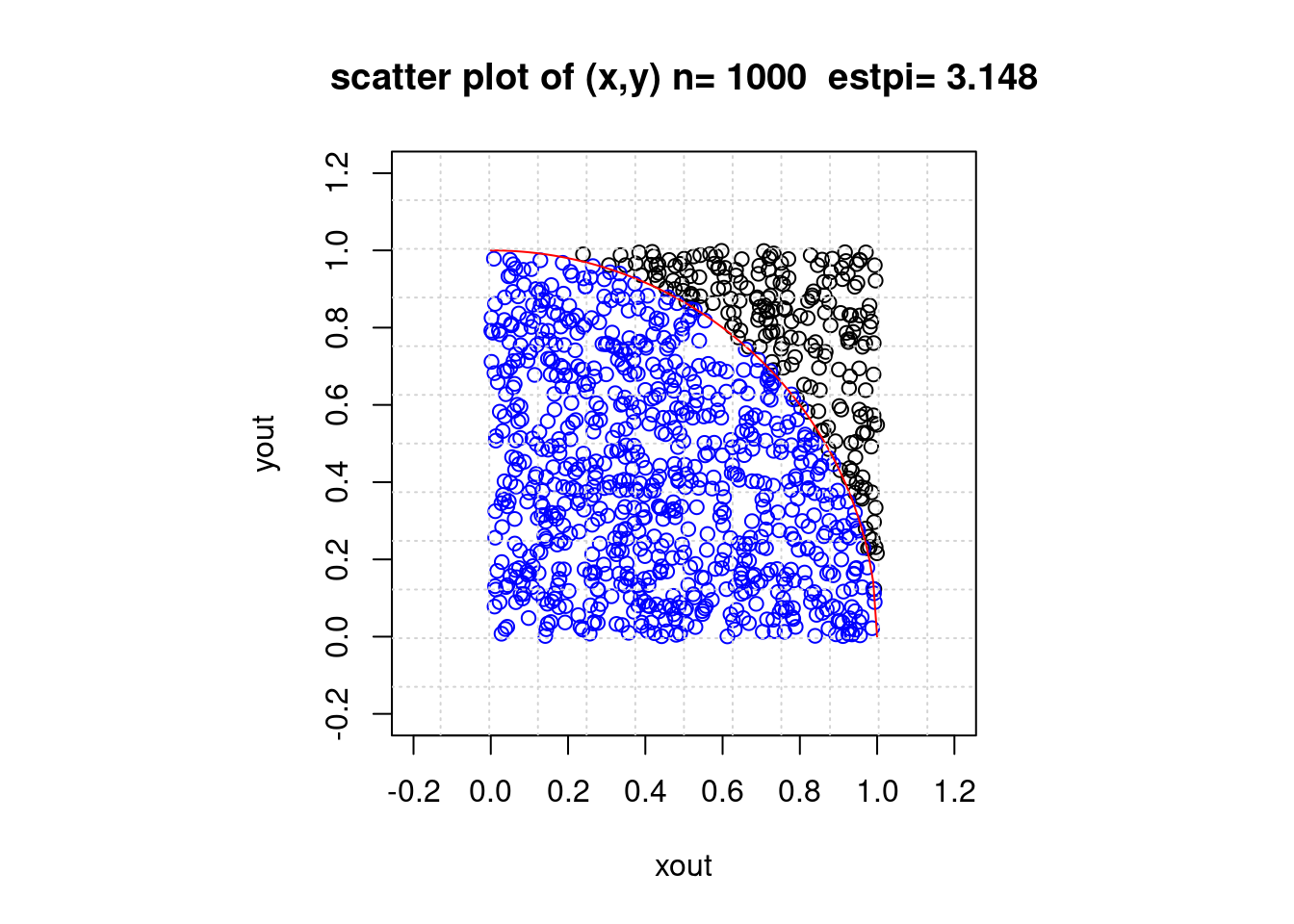
円の最小2乗法
データ \(\{(x_s, y_s), s=1,2,...,n\}\) に対して \(S = \sum_{s=1}^n \{(x_s-x_c)^2 + (y_s-y_c)^2 - r^2\}^2\) を最小にする円の中心座標 \((x_c, y_c)\) と半径 \(r\) を求める.
source("/home/inoue/r-ex/RLIB")
p <- c(xc<-2,yc<-3,r<-4) # (xc,yc,r)
cat("円の母数ベクトル: p=(xc,yc,r)=",p,"\n")## 円の母数ベクトル: p=(xc,yc,r)= 2 3 4cat("母数: xc=",xc,"yc=",yc,"r=",r,"\n")## 母数: xc= 2 yc= 3 r= 4n <- 50; ng <- 200; # n:データ数, ng:円表示点数,
rate <- 3/4 # データの取得範囲を制限できる
t <- seq(0:(n-1))*2*pi/n*rate # 半時計回りの角度 (0 <= t < 2*pi)
tg <- seq(0:(ng-1))*2*pi/ng # 円を描画するための表示点の個数
xt <- xc + r*cos(t); xg <- xc + r*cos(tg)
yt <- yc + r*sin(t); yg <- yc + r*sin(tg)
### 誤差の生成
sd <- 0.5 # sd:誤差の標準偏差
set.seed(1); xeps <- rnorm(n,0,sd=sd) # 正規乱数による誤差
set.seed(2); yeps <- rnorm(n,0,sd=sd) # 正規乱数による誤差
### データの生成
x <- xt + xeps; y <- yt + yeps
### 母数変換 A=-2*xc, B= -2*yc, C=xc^2+yc^2-r^2 後の正規方程式
M <- matrix(0,nrow=3,ncol=3)
M[1,] <- c(sum(x^2), sum(x*y), sum(x))
M[2,] <- c(sum(y*x), sum(y^2), sum(y))
M[3,] <- c(sum(1*x), sum(1*y), n)
b <- c(-sum((x^2+y^2)*x), -sum((x^2+y^2)*y), -sum((x^2+y^2)*1))
ans <- solve(M,b) # 正規方程式を解く
cat("解ベクトル: ans=",ans," (<- 母数変換された解ベクトル)\n")## 解ベクトル: ans= -3.931338 -6.287147 -3.196632 (<- 母数変換された解ベクトル)### 母数逆変換 ans=(A,B,C) -> ph=(xch,ych,rh)
ph <- c(-0.5*ans[1], -0.5*ans[2], sqrt(0.25*ans[1]^2+0.25*ans[2]^2-ans[3]))
cat("推定解ベクトル: ph=",ph,"\n")## 推定解ベクトル: ph= 1.965669 3.143574 4.116132xh <- ph[1] + ph[3]*cos(tg)
yh <- ph[2] + ph[3]*sin(tg)
### 描画
#g.on("fig-1")
par(pty="s",cex=0.75)
plot(x,y,xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r))
main <- "true circle(blue) and estimated circle(red)"
sub <- paste("\n true: (xc, yc, r)=(",p[1],", ",p[2],", ",p[3],
"), n=",n, ", sd=",sd,", rate=",round(rate,3),"\n",
"est.: (xch, ych, rh)=(",
round(ph[1],3),", ",round(ph[2],3),", ",round(ph[3],3),")")
title(main=main,sub=sub)
### 真円描画
xg <- c(xg,xg[1]); yg <- c(yg,yg[1])
par(new=T)
plot(xg,yg,type="l",col="blue",xlab="",ylab="",
xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r))
points(p[1],p[2],col="blue",pch=3)
### 推定円描画
par(new=T)
xh <- c(xh,xh[1]); yh <- c(yh,yh[1])
plot(xh,yh,type="l",col="red",xlab="",ylab="",
,xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r))
points(ph[1],ph[2],col="red",pch=3)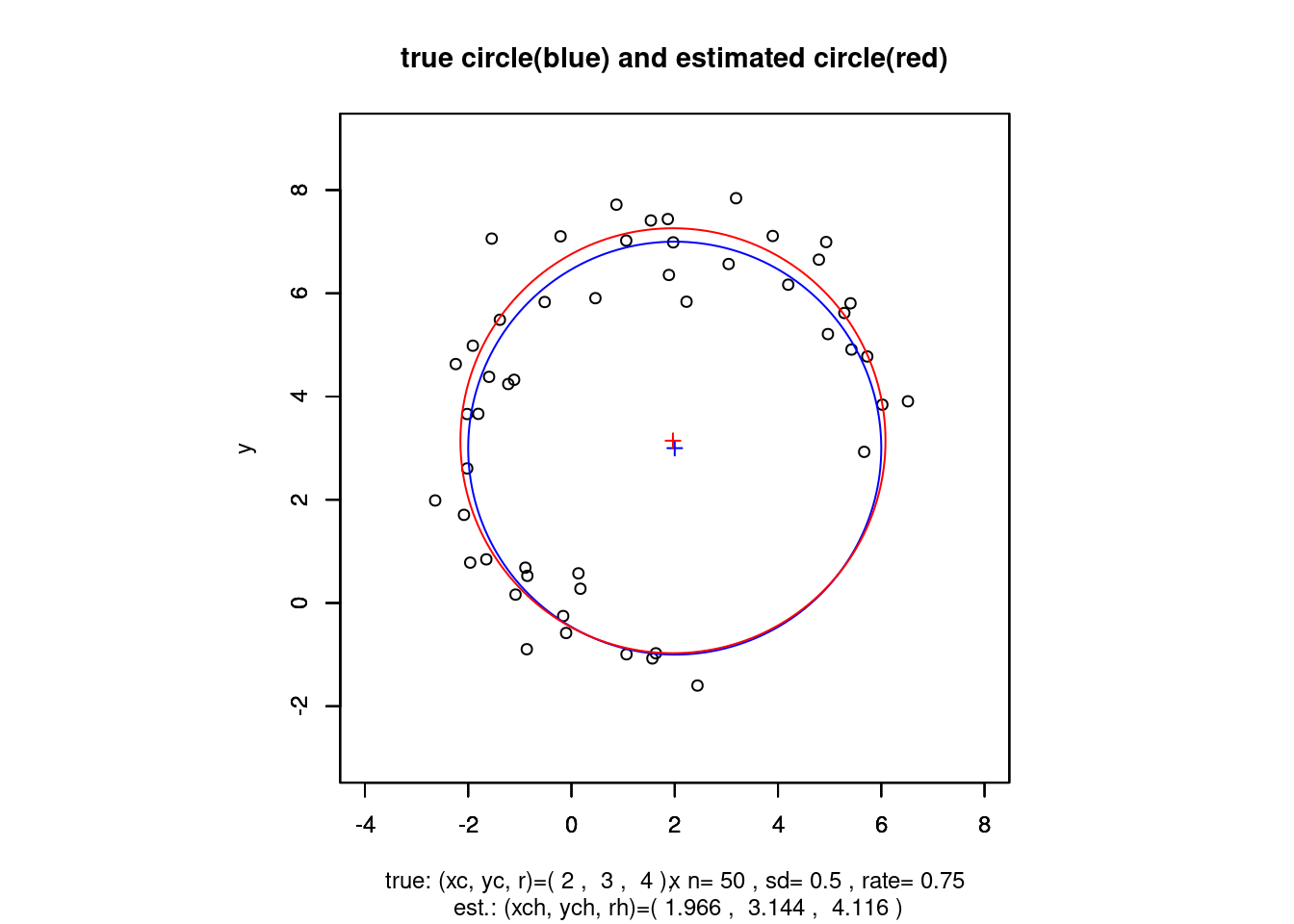
#g.off(); g.view("fig-1");q()球の最小2乗法
データ \(\{(x_s, y_s, z_s), s=1,2,...,n\}\) に対して \(S = \sum_{s=1}^n \{(x_s-x_c)^2 + (y_s-y_c)^2 + (z_s-z_c)^2 - r^2\}^2\) を最小にする球の中心座標 \((x_c, y_c, z_c)\) と半径\(r\)を求める.
source("/home/inoue/r-ex/RLIB")
p <- c(xc<-1,yc<-2,zc<-3,r<-4) # (xc,yc,zc,r)
cat("球の母数ベクトル: p=(xc,yc,zc,r)=",p,"\n")## 球の母数ベクトル: p=(xc,yc,zc,r)= 1 2 3 4cat("母数: xc=",xc,"yc=",yc,"zc=",zc,"r=",r,"\n")## 母数: xc= 1 yc= 2 zc= 3 r= 4# nt: 緯度方向のデータ数, nu: 経度方向のデータ数, n=nt*nu:データ数
nt <- 10; nu <- 20; n <- nt*nu # 0 <= t < pi, 0 <= u < 2*pi
rate <- 1 # 緯度,経度に関するデータ取得率
t <- seq(0:(nt-1))*pi/nt * rate
u <- seq(0:(nu-1))*2*pi/nu * rate
### データ点を作成する
xt <- rep(0,n); yt <- rep(0,n); zt <- rep(0,n)
for (i in 1:nt) {
for (j in 1:nu) {
xt[nu*(i-1)+j] <- xc + r*sin(t[i])*cos(u[j])
yt[nu*(i-1)+j] <- yc + r*sin(t[i])*sin(u[j])
zt[nu*(i-1)+j] <- zc + r*cos(t[i])
}
}
sd <- 0.5 # sd:誤差の標準偏差
set.seed(1); xeps <- rnorm(n,0,sd=sd) # 正規乱数による誤差
set.seed(2); yeps <- rnorm(n,0,sd=sd) # 正規乱数による誤差
set.seed(3); zeps <- rnorm(n,0,sd=sd) # 正規乱数による誤差
### 誤差を伴ったデータベクトル x, y, z (n*1) を生成する
x <- xt + xeps; y <- yt + yeps; z <- zt + zeps
### 描画用作図点を作成する
ngt <- 30; ngu <- 60; ng <- (ngt+1)*(ngu+1)
tg <- seq(0:ngt)*pi/ngt # 球を描画するための表示点の個数(緯度方向)
ug <- seq(0:ngu)*2*pi/ngu # 球を描画するための表示点の個数(経度方向)
### 母数変換 A=-2*xc, B= -2*yc, C = -2*zc, D=xc^2+yc^2+zc^2-r^2 後の正規方程式
M <- matrix(0,nrow=4,ncol=4)
M[1,] <- c(sum(x^2), sum(x*y), sum(x*z), sum(x*1))
M[2,] <- c(sum(y*x), sum(y^2), sum(y*z), sum(y*1))
M[3,] <- c(sum(z*x), sum(z*y), sum(z^2), sum(z*1))
M[4,] <- c(sum(1*x), sum(1*y), sum(1*z), n)
b <- c(-sum((x^2+y^2+z^2)*x), -sum((x^2+y^2+z^2)*y),
-sum((x^2+y^2+z^2)*z), -sum((x^2+y^2+z^2)*1))
ans <- solve(M,b) # 正規方程式を解く
cat("解ベクトル: ans=",ans," (<- 母数変換された解ベクトル)\n")## 解ベクトル: ans= -2.188196 -3.966385 -5.944339 -2.380663 (<- 母数変換された解ベクトル)### 母数逆変換 ans=(A,B,C,D) -> ph=(xch,ych,zch,rh)
ph <- c(-0.5*ans[1], -0.5*ans[2], -0.5*ans[3],
sqrt(0.25*ans[1]^2+0.25*ans[2]^2+0.25*ans[3]^2-ans[4]))
cat("推定解ベクトル: ph=",ph,"\n")## 推定解ベクトル: ph= 1.094098 1.983193 2.972169 4.04284### 推定された球の(x,y,z)座標
xh <- rep(0,ng); yh <- rep(0,ng); zh <- rep(0,ng)
for (i in 1:(ngt+1)) {
for (j in 1:(ngu+1)) {
xh[(ngu+1)*(i-1)+j] <- ph[1] + ph[4]*sin(tg[i])*cos(ug[j])
yh[(ngu+1)*(i-1)+j] <- ph[2] + ph[4]*sin(tg[i])*sin(ug[j])
zh[(ngu+1)*(i-1)+j] <- ph[3] + ph[4]*cos(tg[i])
}
}
### 真球の(x,y,z)座標
xg <- rep(0,ng); yg <- rep(0,ng); zg <- rep(0,ng)
for (i in 1:(ngt+1)) {
for (j in 1:(ngu+1)) {
xg[(ngu+1)*(i-1)+j] <- xc + r*sin(tg[i])*cos(ug[j])
yg[(ngu+1)*(i-1)+j] <- yc + r*sin(tg[i])*sin(ug[j])
zg[(ngu+1)*(i-1)+j] <- zc + r*cos(tg[i])
}
}
#g.on("fig-2",height=27)
library(scatterplot3d)
par(mfrow=c(3,1),cex=0.7,pty="s") # pty="s"
scatterplot3d(x,y,z,
xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r),
zlim=c(zc-1.5*r,zc+1.5*r))
main=paste("Data: (x_s, y_s, z_s), s=1, 2, ..., n, where n=", n)
title(main=main)
### 真球描画
scatterplot3d(xg,yg,zg,highlight.3d=T,col.grid="blue",
xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r),
zlim=c(zc-1.5*r,zc+1.5*r))
main <- paste("True Sphere (xc=",p[1],", yc=",p[2],", zc=",p[3],", r=",p[4],")")
title(main=main)
### 推定球描画
scatterplot3d(xh,yh,zh,highlight.3d=T,
xlim=c(xc-1.5*r,xc+1.5*r),ylim=c(yc-1.5*r,yc+1.5*r),
zlim=c(zc-1.5*r,zc+1.5*r))
main <- paste("Estimated Sphere (xc=",round(ph[1],3),
", yc=",round(ph[2],3),", zc=",round(ph[3],3),
", r=",round(ph[4],3),")")
title(main=main)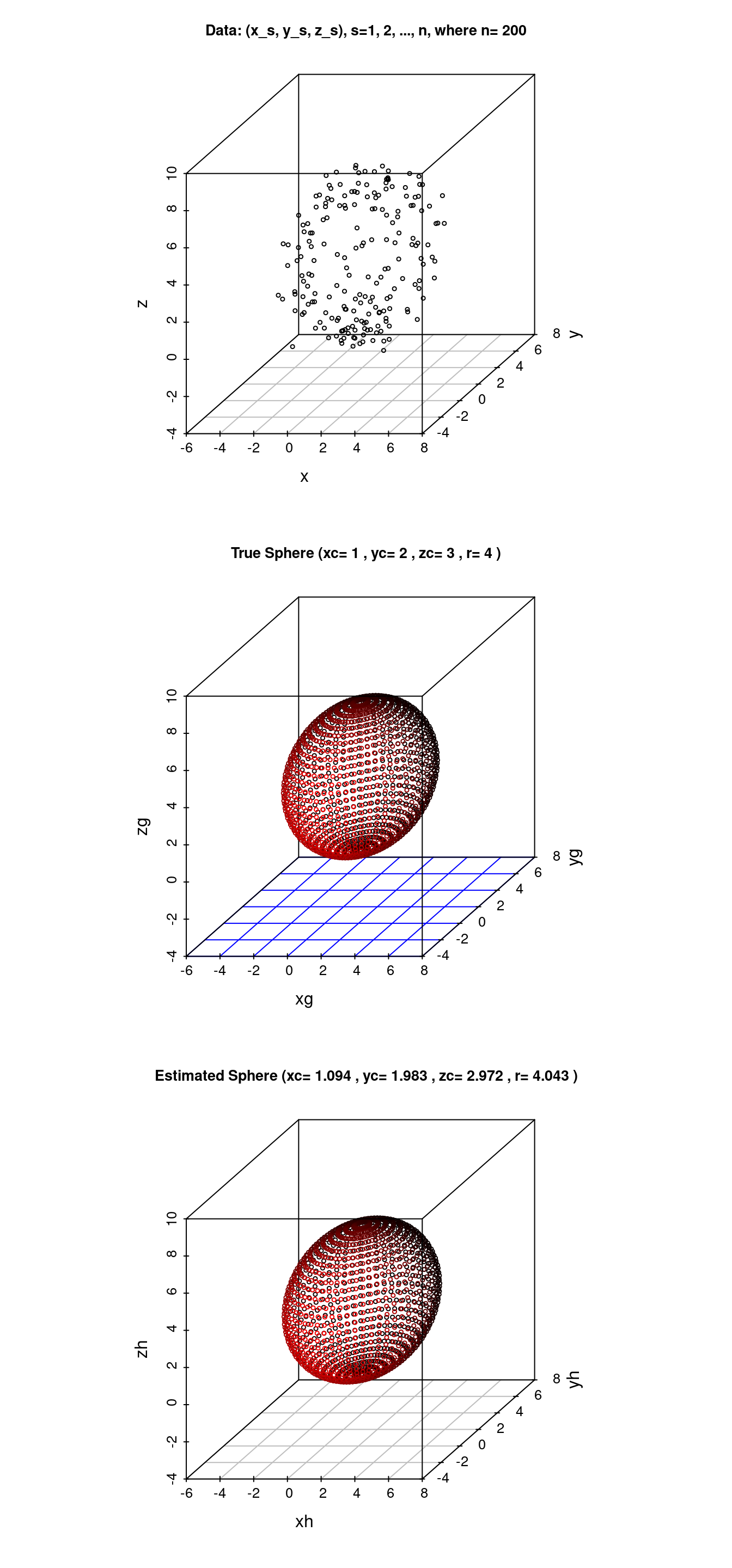
R言語私用ライブラリRLIBのメモ: ex-persp.Rnw
関数 persp() の定義
methods(persp)## [1] persp.default*
## see '?methods' for accessing help and source codegetS3method("persp","default")## function (x = seq(0, 1, length.out = nrow(z)), y = seq(0, 1,
## length.out = ncol(z)), z, xlim = range(x), ylim = range(y),
## zlim = range(z, na.rm = TRUE), xlab = NULL, ylab = NULL,
## zlab = NULL, main = NULL, sub = NULL, theta = 0, phi = 15,
## r = sqrt(3), d = 1, scale = TRUE, expand = 1, col = "white",
## border = NULL, ltheta = -135, lphi = 0, shade = NA, box = TRUE,
## axes = TRUE, nticks = 5, ticktype = "simple", ...)
## {
## if (is.null(xlab))
## xlab <- if (!missing(x))
## deparse1(substitute(x))
## else "X"
## if (is.null(ylab))
## ylab <- if (!missing(y))
## deparse1(substitute(y))
## else "Y"
## if (is.null(zlab))
## zlab <- if (!missing(z))
## deparse1(substitute(z))
## else "Z"
## if (missing(z)) {
## if (!missing(x)) {
## if (is.list(x)) {
## z <- x$z
## y <- x$y
## x <- x$x
## }
## else {
## z <- x
## x <- seq.int(0, 1, length.out = nrow(z))
## }
## }
## else stop("no 'z' matrix specified")
## }
## else if (is.list(x)) {
## y <- x$y
## x <- x$x
## }
## if (any(diff(x) <= 0) || any(diff(y) <= 0))
## stop("increasing 'x' and 'y' values expected")
## if (box) {
## zz <- z[!is.na(z)]
## if (any(x < xlim[1]) || any(x > xlim[2]) || any(y < ylim[1]) ||
## any(y > ylim[2]) || any(zz < zlim[1]) || any(zz >
## zlim[2]))
## warning("surface extends beyond the box")
## }
## ticktype <- pmatch(ticktype, c("simple", "detailed"))
## plot.new()
## r <- .External.graphics(C_persp, x, y, z, xlim, ylim, zlim,
## theta, phi, r, d, scale, expand, col, border, ltheta,
## lphi, shade, box, axes, nticks, ticktype, as.character(xlab),
## as.character(ylab), as.character(zlab), ...)
## for (fun in getHook("persp")) {
## if (is.character(fun))
## fun <- get(fun)
## try(fun())
## }
## if (!is.null(main) || !is.null(sub))
## title(main = main, sub = sub, ...)
## invisible(r)
## }
## <bytecode: 0x563865ab1bf0>
## <environment: namespace:graphics>require(grDevices) # for trans3d
trans3d # trans3d の定義## function (x, y, z, pmat, continuous = FALSE, verbose = TRUE)
## {
## tr <- cbind(x, y, z, 1, deparse.level = 0L) %*% pmat
## if (continuous && (n <- nrow(tr)) >= 2) {
## st4 <- sign(tr[, 4])
## if ((s1 <- st4[1]) != st4[n]) {
## if ((last <- (which.min(st4 == s1) - 1L)) >= 1L) {
## if (verbose)
## message(sprintf("points cut off after point[%d]",
## last))
## tr <- tr[seq_len(last), , drop = FALSE]
## }
## }
## }
## list(x = tr[, 1]/tr[, 4], y = tr[, 2]/tr[, 4])
## }
## <bytecode: 0x563865b5cdd8>
## <environment: namespace:grDevices>#getS3method("trans3d","graphics")使用例
require(grDevices) # for trans3d
## More examples in demo(persp) !!
## -----------
# (1) The Obligatory Mathematical surface.
# Rotated sinc function.
x <- seq(-10, 10, length= 30)
y <- x
f <- function(x, y) { r <- sqrt(x^2+y^2); 10 * sin(r)/r }
z <- outer(x, y, f)
z[is.na(z)] <- 1
op <- par(bg = "white")
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")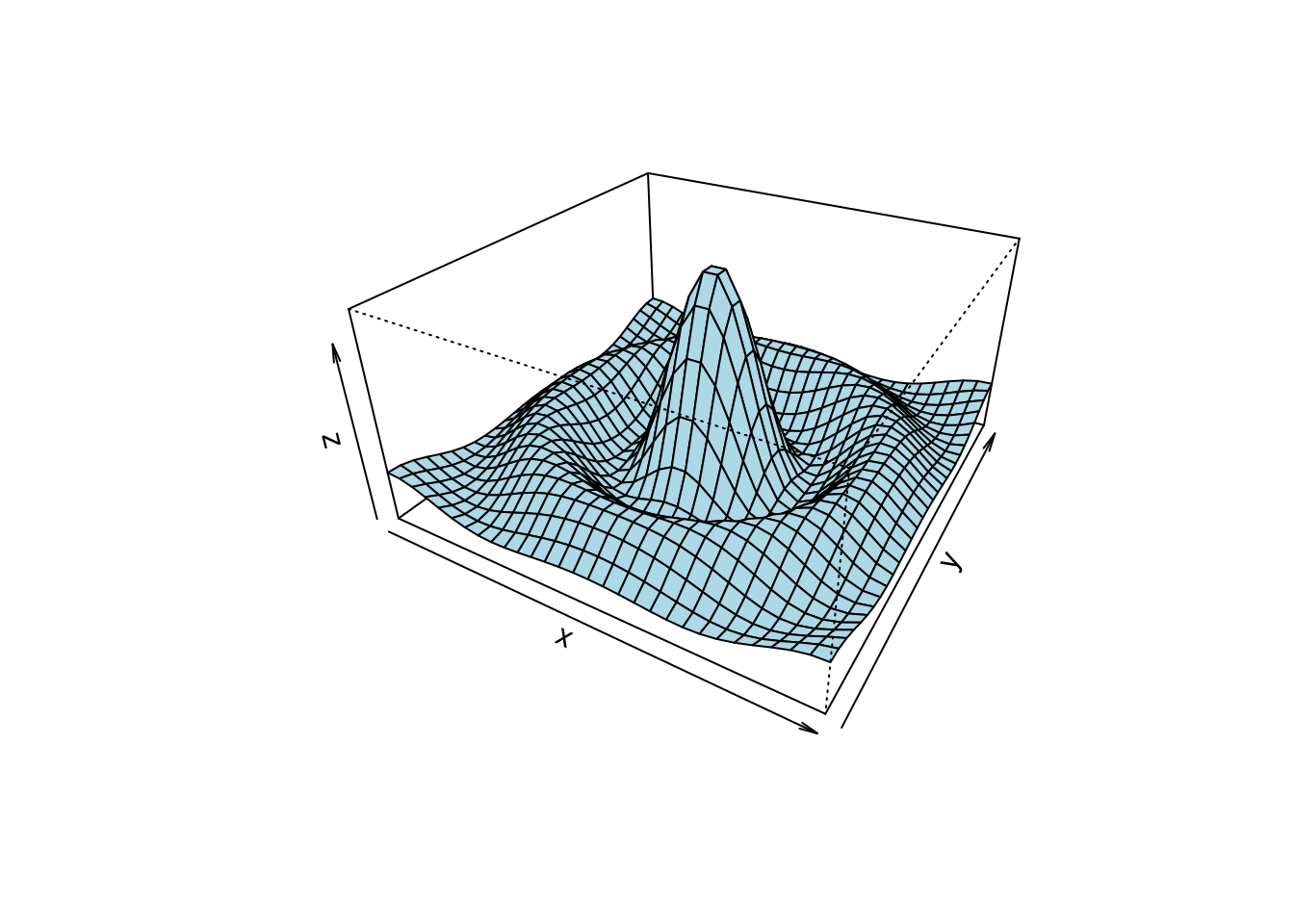
# 第2図
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue",
ltheta = 120, shade = 0.75, ticktype = "detailed",
xlab = "X", ylab = "Y", zlab = "Sinc( r )"
) -> res
round(res, 3)## [,1] [,2] [,3] [,4]
## [1,] 0.087 -0.025 0.043 -0.043
## [2,] 0.050 0.043 -0.075 0.075
## [3,] 0.000 0.074 0.042 -0.042
## [4,] 0.000 -0.273 -2.890 3.890 # (2) Add to existing persp plot - using trans3d() :
xE <- c(-10,10); xy <- expand.grid(xE, xE)
### 4隅に赤点をプロット
points(trans3d(xy[,1], xy[,2], 6, pmat = res), col = 2, pch = 16)
### 側面(y=10)に緑のサインカーブを追加描画
lines (trans3d(x, y = 10, z = 6 + sin(x), pmat = res), col = 3)
### 第2最大値をとる曲線をピンクで描画(等高線描画)
phi <- seq(0, 2*pi, len = 201)
r1 <- 7.725 # radius of 2nd maximum
xr <- r1 * cos(phi)
yr <- r1 * sin(phi)
lines(trans3d(xr,yr, f(xr,yr), res), col = "pink", lwd = 2)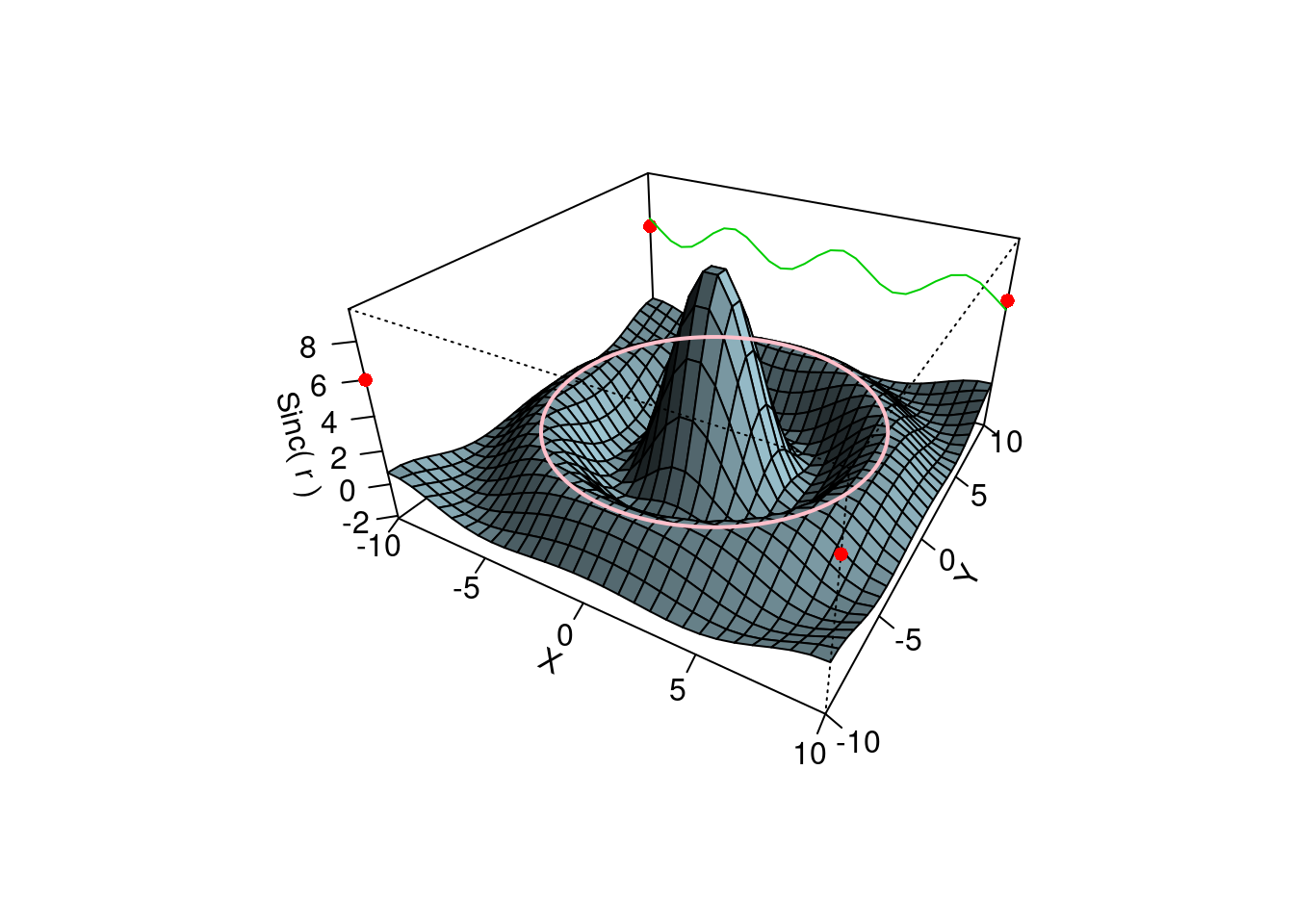
## (no hidden lines)
# (3) Visualizing a simple DEM model
z <- 2 * volcano # Exaggerate the relief
x <- 10 * (1:nrow(z)) # 10 meter spacing (S to N)
y <- 10 * (1:ncol(z)) # 10 meter spacing (E to W)
## Don't draw the grid lines : border = NA
par(bg = "slategray")
persp(x, y, z, theta = 135, phi = 30, col = "green3", scale = FALSE,
ltheta = -120, shade = 0.75, border = NA, box = FALSE)
# (4) Surface colours corresponding to z-values
par(bg = "white")
x <- seq(-1.95, 1.95, length = 30)
y <- seq(-1.95, 1.95, length = 35)
z <- outer(x, y, function(a, b) a*b^2)
nrz <- nrow(z)
ncz <- ncol(z)
# Create a function interpolating colors in the range of specified colors
jet.colors <- colorRampPalette( c("blue", "green") )
# Generate the desired number of colors from this palette
nbcol <- 100
color <- jet.colors(nbcol)
# Compute the z-value at the facet centres
zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz]
# Recode facet z-values into color indices
facetcol <- cut(zfacet, nbcol)
persp(x, y, z, col = color[facetcol], phi = 30, theta = -30)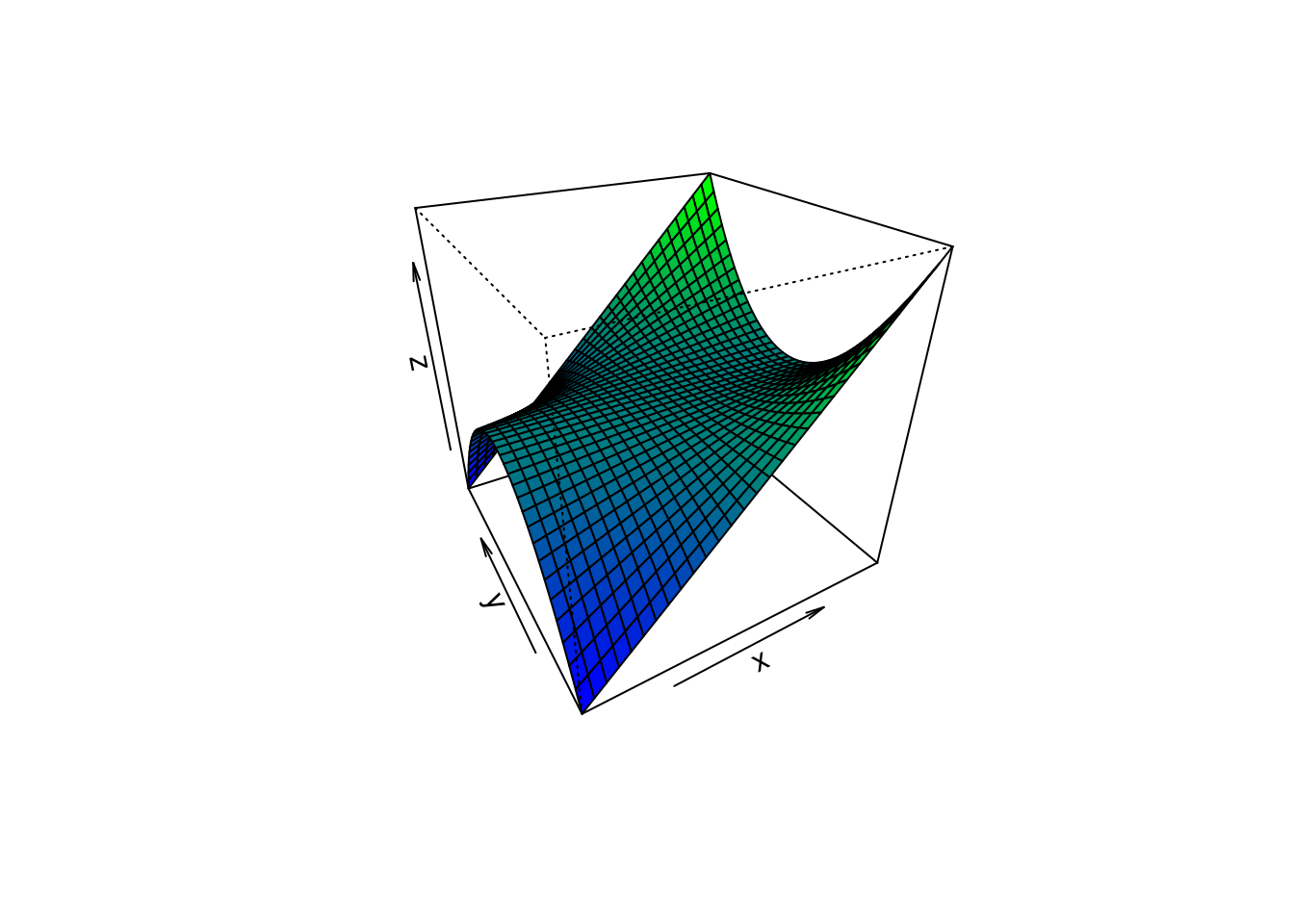
par(op)2変量正規分布と条件付き分布,周辺分布
### plot3func 2変数関数の鳥瞰図,等高線図の作図 #############
plot3func <- function(xlim,ylim,func,contour=T,...){
gx <- seq(xlim[1],xlim[2],length=51)
gy <- seq(ylim[1],ylim[2],length=51)
gz <- outer(gx,gy, func)
op <- par(no.readonly=TRUE)
if (contour) {
mat <- matrix(c(1,1,1,0,0, 1,1,1,2,2, 1,1,1,2,2,
1,1,1,2,2, 1,1,1,0,0), ncol=5, byrow=T)
layout(mat)
}
persp(gx, gy, gz, xlim=xlim, ylim=ylim,
xlab="x", ylab="y", zlab="Dens.",
theta=30, phi=30,
ticktype="detailed", nticks=3,
expand=0.5, shade=0.5, col="cyan",...)
if (contour) {
par(pty="s")
gx <- seq(xlim[1],xlim[2],length=101)
gy <- seq(ylim[1],ylim[2],length=101)
gz <- outer(gx,gy, func)
# levels <- seq(0, max(gz)*0.7,length=7)
# contour(gx, gy, gz, xlab="x", ylab="y",levels=levels)
image(gx, gy, gz, xlab="x", ylab="y",
col = c("gray", heat.colors(12)) )
}
par(op)
}
##########################################
func.xy <- function(x,y){ # 2変量度数分布表から同時密度関数を生成
f <- rep(0, length(x)); ie <- length(xbrk)-1; je <- length(ybrk)-1
for (i in 1:ie) {
for (j in 1:je) {
fx <- -1*(x-xbrk[i])*(x-xbrk[i+1]); fx <- round(fx,3);
fy <- -1*(y-ybrk[j])*(y-ybrk[j+1]); fy <- round(fy,3)
# cat("fun: fx", fx, "\n")
for (s in 1:length(x)) {
if ( (fx[s] >= 0) & (fy[s] >= 0) ) {
f[s] <- fxy[i,j]/(xbrk[i+1]-xbrk[i])/(ybrk[j+1]-ybrk[j]) }
} # end of for-s
} # end of for-j
} # end of for-i
#cat("fun: z ",f,"\n")
return(f)
} # end of fun
### dnorm2 : 2変量正規分布の密度関数
dnorm2 <- function(x, y, means=c(0,0), sds=c(1,1), cor=0){
mux <- means[1]; sdx <- sds[1]
muy <- means[2]; sdy <- sds[2]
#cat("func: x ",x,"\n")
#cat("func: y ",y,"\n")
f1 <- 2*pi * sdx * sdy * sqrt(1-cor^2)
f2 <- ((x-mux)/sdx)^2 - 2*cor*((x-mux)/sdx)*((y-muy)/sdy) + ((y-muy)/sdy)^2
f2 <- exp(-0.5 / (1-cor^2) * f2)
f <- f2/f1
#cat("func: z ",f,"\n")
return(f)
}
###### main #########################################################
require(grDevices)
par(family="Japan1",mfrow=c(1,1))
cor <- 0.7
f <- function(x,y){ dnorm2(x,y,means=c(0,0),sds=c(1,1),cor=cor)}
x <- seq(-4,4,length=51)
y <- seq(-4,4,length=51)
z <- outer(x,y,f); z[is.na(z)] <- 0;
### 同時密度関数 z=f(x,y)
xlim <- range(x); ylim <- range(y); zlim <- c(min(z), max(z)*1.05)
plot3func(xlim,ylim,f,contour=T) ### 私用関数による描画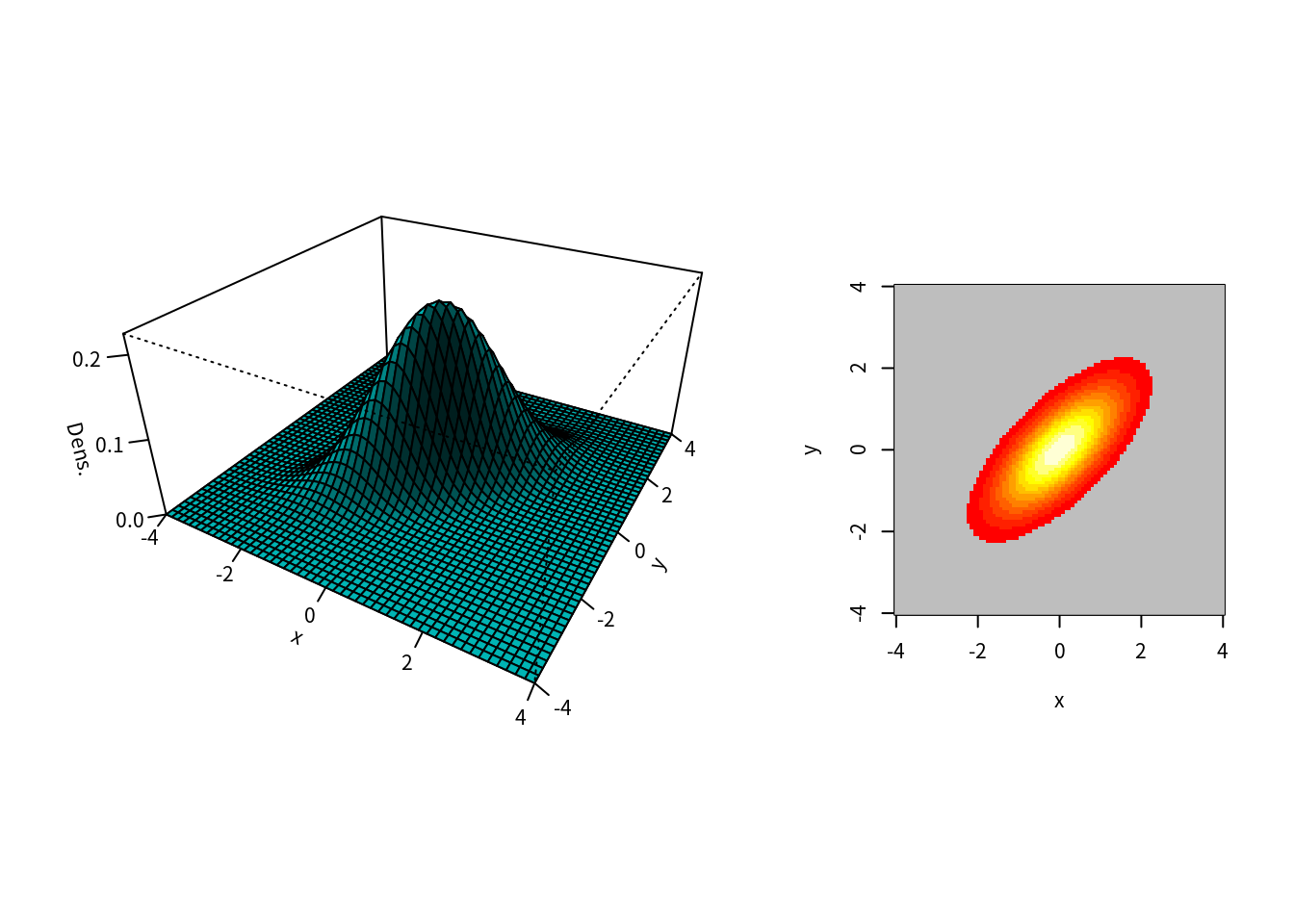
op <- par(bg="white",family="Japan1")
main <- "同時密度関数: f(x,y)"
res <- persp(x,y,z,theta=30,phi=30,expand=0.5,col="lightblue",
ltheta=120,shade=0.75,ticktype="detailed",
xlim=xlim,ylim=ylim,zlim=zlim,main=main,
xlab="x",ylab="y",zlab="f(x,y)")
round(res,3) ### 3次元データ(x,y,z)を平面に投影する情報をresに保存## [,1] [,2] [,3] [,4]
## [1,] 0.217 -0.062 0.108 -0.108
## [2,] 0.125 0.108 -0.188 0.188
## [3,] 0.000 3.701 2.137 -2.137
## [4,] 0.000 -0.433 -2.982 3.982### 切断面を描画 (pmat=res で使用)
x0 <- 1; y0 <- -1; zmin <- min(z); zmax <- max(z)
lines(trans3d(x,y=y0,z=f(x,y0),pmat=res),col="red",lwd=2)
lines(trans3d(x,y=y0,z=0,pmat=res),col="red",lwd=1)
lines(trans3d(x,y=y0,z=zmax,pmat=res),col="red",lwd=1)
lines(trans3d(x=xlim[1],y=y0,z=c(zmin,zmax),pmat=res),col="red",lwd=1)
lines(trans3d(x=xlim[2],y=y0,z=c(zmin,zmax),pmat=res),col="red",lwd=1)
lines(trans3d(x=x0,y,z=f(x0,y),pmat=res),col="blue",lwd=2)
lines(trans3d(x=x0,y,z=0,pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y,z=zmax,pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y=ylim[1],z=c(zmin,zmax),pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y=ylim[2],z=c(zmin,zmax),pmat=res),col="blue",lwd=1)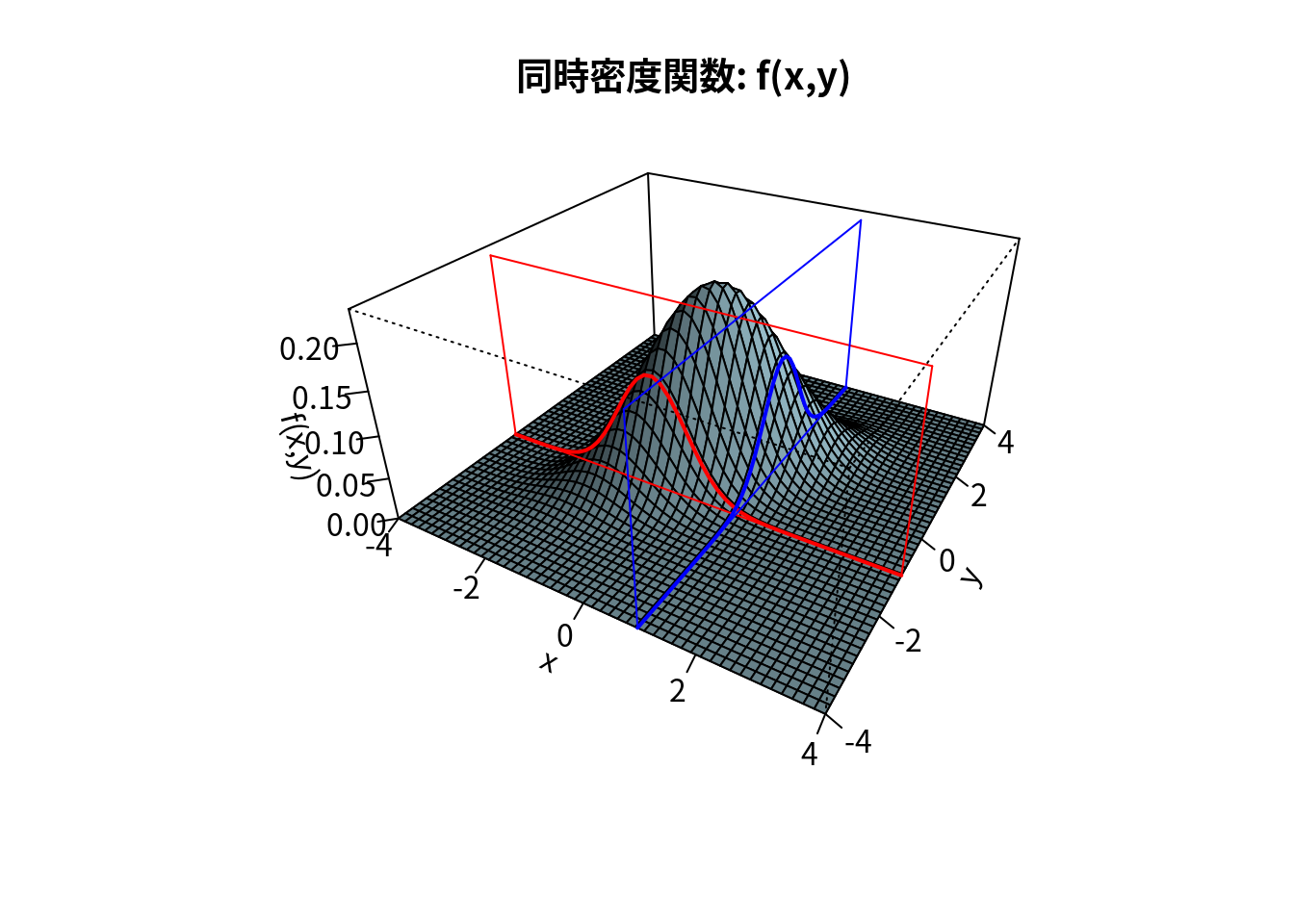
######################
x <- seq(-4,4,length=51)
y <- seq(-4,4,length=51)
f0 <- function(x,y) { x+y-x-y }
z <- outer(x,y,f); z[is.na(z)] <- 0;
xlim <- range(x); ylim <- range(y);
op <- par(bg="white",family="Japan1")
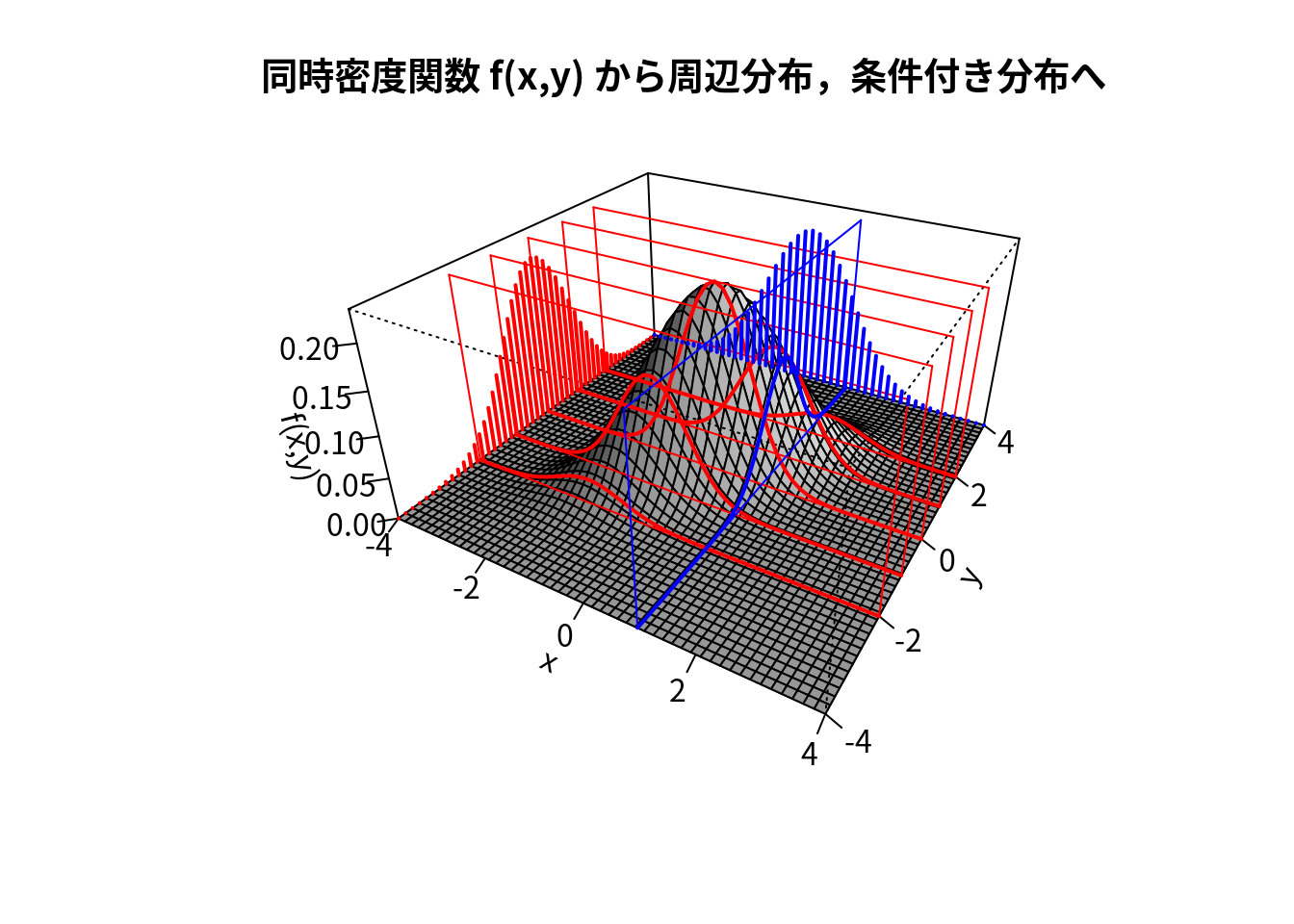
main <- "同時密度関数 f(x,y) から周辺分布,条件付き分布へ"
res <- persp(x,y,z,theta=30,phi=30,expand=0.5,col="white",
ltheta=120,shade=0.75,ticktype="detailed",
xlim=xlim,ylim=ylim,zlim=zlim,main=main,
xlab="x",ylab="y",zlab="f(x,y)")
round(res,3)## [,1] [,2] [,3] [,4]
## [1,] 0.217 -0.062 0.108 -0.108
## [2,] 0.125 0.108 -0.188 0.188
## [3,] 0.000 3.701 2.137 -2.137
## [4,] 0.000 -0.433 -2.982 3.982for (y0 in c(-2,-1,0,1,2)) { ### y=y0 での切断面を描画
lines(trans3d(x,y=y0,z=f(x,y0),pmat=res),col="red",lwd=2)
lines(trans3d(x,y=y0,z=0,pmat=res),col="red",lwd=1)
lines(trans3d(x,y=y0,z=zmax,pmat=res),col="red",lwd=1)
lines(trans3d(x=xlim[1],y=y0,z=c(zmin,zmax),pmat=res),col="red",lwd=1)
lines(trans3d(x=xlim[2],y=y0,z=c(zmin,zmax),pmat=res),col="red",lwd=1)
}
for (y0 in y) { ### y側面にy周辺分布のイメージを描画
fx <- function(x){f(x,y=y0)}
integ <- integrate(fx, -4,4); v <- integ$value/2 #
lines(trans3d(x=xlim[1],y=y0,z=c(zmin,v),pmat=res),col="red",lwd=2)
}
for (x0 in c(1)) { ### x=x0 での切断面を描画
lines(trans3d(x=x0,y,z=f(x0,y),pmat=res),col="blue",lwd=2)
lines(trans3d(x=x0,y,z=0,pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y,z=zmax,pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y=ylim[1],z=c(zmin,zmax),pmat=res),col="blue",lwd=1)
lines(trans3d(x=x0,y=ylim[2],z=c(zmin,zmax),pmat=res),col="blue",lwd=1)
}
for (x0 in x) { ### x側面にx周辺分布のイメージを描画
fy <- function(y){f(x=x0,y)}
integ <- integrate(fy, -4,4); v <- integ$value/2
lines(trans3d(x=x0,y=ylim[2],z=c(zmin,v),pmat=res),col="blue",lwd=2)
}
####### 切断面関数の2次元描画
x0 <- 1; y0 <- -2; par(mfrow=c(2,2),family="Japan1")
x <- seq(-4,4,length=100); zx <- f(x,y=y0)
main <- paste("切断面関数:f(x,y=",y0,")")
plot(x,zx,ylim=zlim,type="l",col="red",ylab="",main=main)
y <- seq(-4,4,length=100); zy <- f(x=x0,y)
main <- paste("切断面関数 : f(x=",x0,",y)")
plot(y,zy,ylim=zlim,type="l",col="blue",ylab="",main=main)
### 条件付き密度関数
fx <- function(x){f(x,y=y0)}
integ <- integrate(fx, -4,4); zx0 <- integ$value
main <- paste("条件付き密度関数:f(x|y=",y0,")")
plot(x,zx/zx0,ylim=c(0,0.7),type="l",col="red",ylab="",main=main)
fy <- function(y){f(x=x0,y)}
integ <- integrate(fy, -4,4); zy0 <- integ$value
main <- paste("条件付き密度関数:f(y|x=",x0,")")
plot(y,zy/zy0,ylim=c(0,0.7),type="l",col="blue",ylab="",main=main)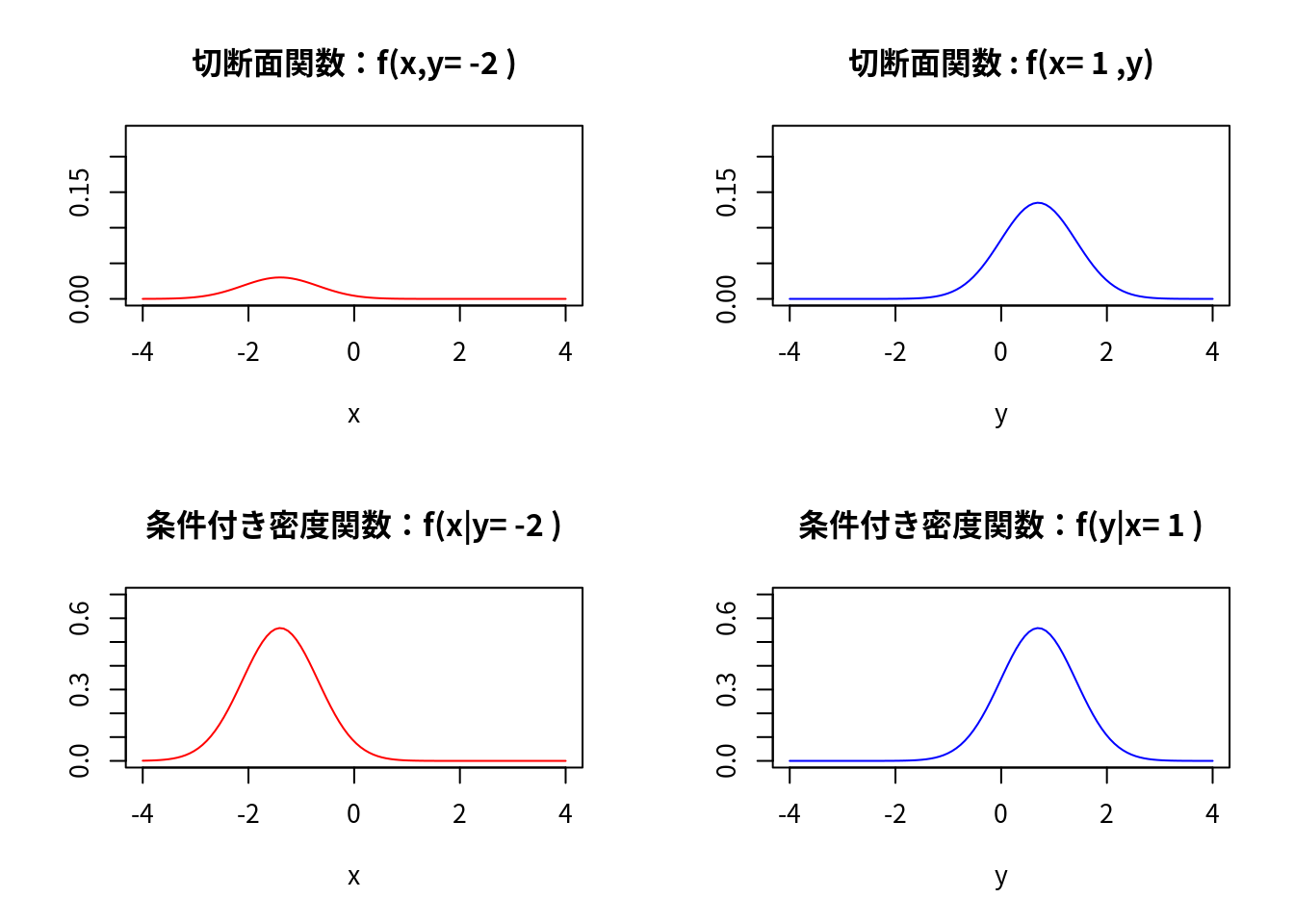
par(mfrow=c(1,2),family="Japan1")
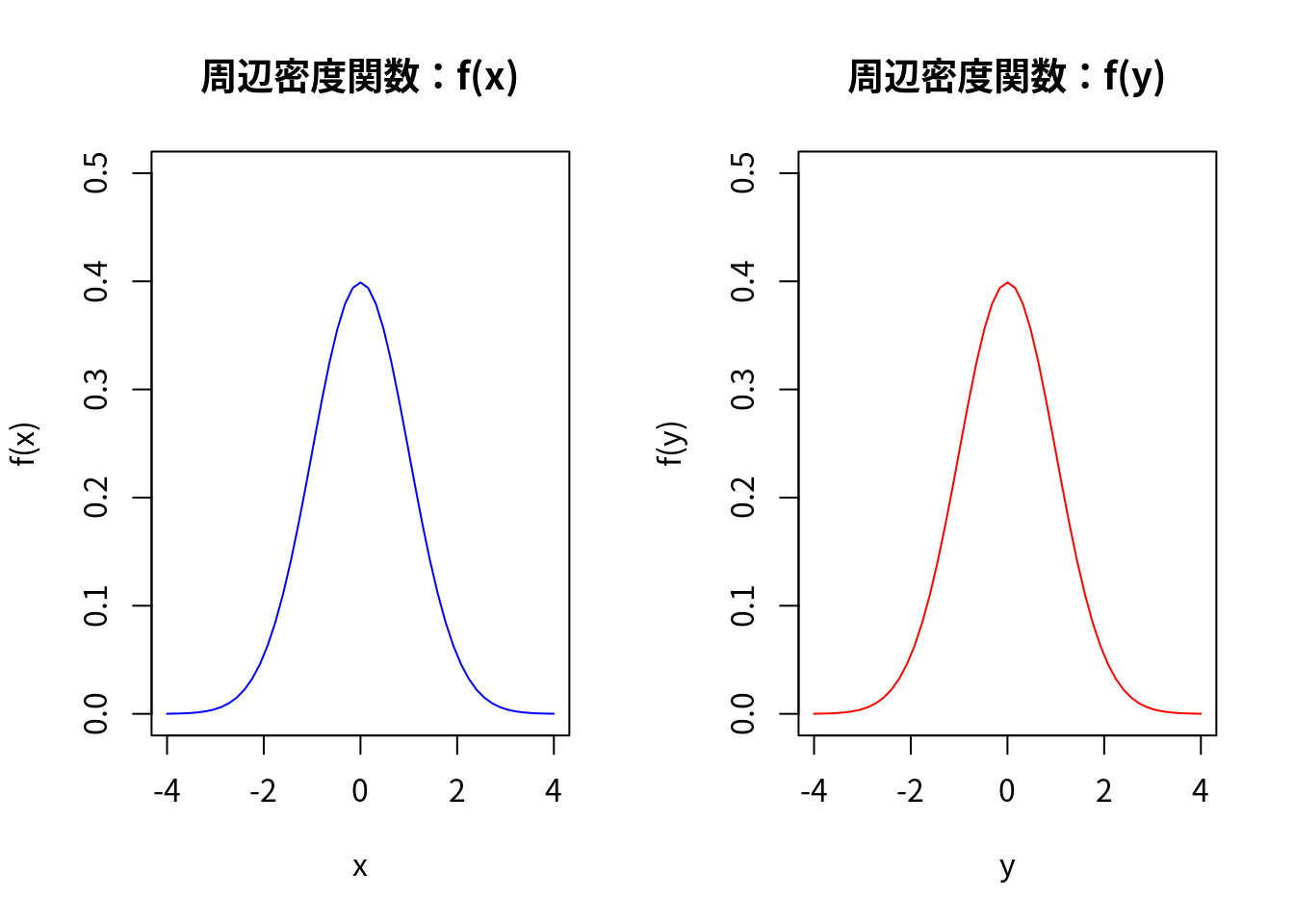
### 周辺密度関数 f(x) の描画
vx <- seq(-4,4,length=51); vf <- rep(0,51)
for (i in 1:length(vx)) {
fy <- function(y){f(x=vx[i],y)};
integ <- integrate(fy, -4,4); vf[i] <- integ$value
}
main <- "周辺密度関数:f(x)"
plot(vx,vf,type="l",xlab="x",ylab="f(x)",ylim=c(0,0.5),col="blue",main=main)
### 周辺密度関数 f(y) の描画
vy <- seq(-4,4,length=51); vf <- rep(0,51)
for (i in 1:length(vy)) {
fx <- function(x){f(x,y=vy[i])}
integ <- integrate(fx, -4,4); vf[i] <- integ$value
}
main <- "周辺密度関数:f(y)"
plot(vy,vf,type="l",xlab="y",ylab="f(y)",ylim=c(0,0.5),col="red",main=main)