R-ref2018.Rmd

  Top   PageTop   PageEnd

1 はじめに

R言語（あーるげんご）はオープンソース・フリーソフトウェアの統計解析向けのプログラミング言語及びその開発実行環境である。
R言語はニュージーランドのオークランド大学のRoss IhakaとRobert Clifford Gentlemanにより作られた。現在ではR Development Core Team（S言語開発者であるJohn M. Chambersも参画している[1]。）によりメンテナンスと拡張がなされている。
なお、R言語の仕様を実装した処理系の呼称名はプロジェクトを支援するフリーソフトウェア財団によれば『GNU R』である[2]が、他の実装形態が存在しないために日本語での慣用的呼称に倣って、当記事では、仕様・実装を纏めて適宜にR言語や単にR等と呼ぶ。 (Wikipediaより引用)

1.1 R言語の統計電卓的機能

  ＊＊＊＊＊＊＊ R (統計電卓）＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
  準備: # comment,  options(echo=F):非表示, system("ls")
  定数：pi, exp(1), ヘルプ：?plot <-- x, plot apropos("read")
  ライブラリ： source("RLIB"), library(xtable),
  例: x <- c(1,2,3); mean(x); var(x); length(x),stem(x); q();
  分布: 密度 dnorm(x),下側確率 pnorm(x),%点 qnorm(p), 乱数 rnorm(n)
  作図：g.on(); curve(sin(x),0,4*pi);g.view();
  ソート: sort(a), order(a), unique(a), duplicate(a)
  方程式：solve(A, c(b1,b2)) <--- A x = b
  行列：A <- matrix(c(a11,a12,a21,a22), ncol=2, byrow=T)
        diag(c(a11,a22)), t(A), solve(A), eigen(A), svd(A)
        rbind(A,B), cbind(A, B), rep(x,n)
  ファイル：sink("out");  ... sink();
  ユーザ関数：ls(), 関数定義：関数名,　ライブラリ一覧: library()  
  関数内容表示:関数名， methods(func), getS3method("func","class")
    methods(predict), getS3method("predict","smooth.spline")
  ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊(T.INOUE)＊＊

1.2 R言語ヘルプ機能

ヘルプコマンド一覧(h.s:help.search, sea:search, obj:object の省略形)
   1．h.s("linear models")  説明に"linear models"を含む文献を検索
   2．ls()                   オブジェクト(ユーザ関数）一覧
   3. 関数名                 関数()の定義を表示
   4. library()              ライブラリ一覧
   5．sea()                  パッケージ一覧
   6．obj(7)                 7番目のパッケージ内のオブジェクトを表示
   7．obj(7,pattern="sta") パッケージ内の"sta"で始まるオブジェクトを表示
   hlp("intro")   : メモ全般        hlp("const")   : 定数
   hlp("func")    : R-組み込み関数  hlp("sort")    : ソート関数
   hlp("rstat")   : R-基本統計関数  hlp("dist")    : 確率分布一覧    
   hlp("vect")    : ベクトル        hlp("matrix")  : 行列/配列
   hlp("list")    : リスト          hlp("df")      : データフレーム  
   hlp("object")  : オブジェクト/型変換
   hlp("program") : プログラミング  hlp("string")  : 文字列操作
   hlp("plot")    : 作図関数        hlp("rnw")     : Sweave(TeX)
   hlp("mylib")   : 私的ライブラリ  hlp("myenv")   : 私的環境 \n" 

  Top   PageTop   PageEnd

2 R言語の言語仕様

2.1 定数

   pi                 : 円周率,                exp(1)             : 自然対数の底
   LETTERS            : アルファベット大文字   letters            : アルファベット小文字
   month.abb          : 月の英語略号           month.name         : 月の英語名
   TRUE (T)           : 真(論理値)             FALSE (F)          : 偽(論理値)
   NA (Not Available) : 数値の欠側値           NaN (Not a Number) : 非数値の欠側値
   NULL               : 未定義                 Inf                : 無限大

pi         # 円周率

## [1] 3.141593

exp(1)     # 自然対数の底

## [1] 2.718282

LETTERS    # アルファベット大文字

##  [1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N" "O" "P" "Q" "R" "S"
## [20] "T" "U" "V" "W" "X" "Y" "Z"

month.abb  # 月の英語略号

##  [1] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec"

2.2 R言語仕様:原子的なデータ型

R言語ではデータを記述する原子(基本)的なデータ型として
　　　NULL(空値), logical(論理値), numeric(整数，実数), complex(複素数), character(文字列)
が用意され，それらはmode()で確認することができる．また，numeric(整数，実数)にはデータ型の分類とは別に内部メモリーモードがあり，整数型integerと実数型(倍精度不動小数点型)doubleがあり，それらはtypeof()で確認できる．さらに，カテゴリカルデータを記述するための関数factor()が用意されている．

上記の原子的データの並びに構造を持たせたもの(データ構造)として
　　(スカラー)，ベクトル，行列，配列，データフレーム，リスト
が用意され，それらのデータ型，データ構造の確認や変換をおこなう関数is.???(), as.??? が用意されている．加えて，文字列操作関数や文字列を式に変換しR言語で評価する関数parse(), eval()なども用意されている．

R言語では，データの並びや関数を含めすべてを“オブジェクト”と呼ぶ．オブジェクトには“クラス”class()と“長さ”length()がある．Rは，ベクトルを処理単位とする言語(オブジェクト指向言語)である． オブジェクトには“モード”mode()と“属性”attributes()がある．

• データ型モード: NULL, logical, numeric, complex, character
• 言語オブジェクト:　function, expression

(M <- matrix(1:6, ncol=3, byrow=T))   # (2x3)行列 M を定義

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

class(M)       # クラス

## [1] "matrix"

length(M)      # 長さ

## [1] 6

mode(M)        # モード

## [1] "numeric"

attributes(M)  # 属性

## $dim
## [1] 2 3

str(M)　       # オブジェクトの構造をモード，属性，要約データを表示する

##  int [1:2, 1:3] 1 4 2 5 3 6

データ型モード:NULL(空値), logical(論理値), numeric(整数，実数), complex(複素数), character(文字列)には，その表現力から自然な包含関係
　　NULL　< logical　< numeric　< complex　< character
をもつ．例えば文字列“1+2i”は複素数を表現でき，複素数“1+0i”は実数を表現できる．

x <- "1+2i"      # 文字列
mode(x)          # モード

## [1] "character"

as.complex(x)    # 複素数に変換

## [1] 1+2i

as.complex(x)*2  # 複素数化の後に演算

## [1] 2+4i

as.numeric(1+0i) # 実数化

## [1] 1

numeric(整数，実数)にはデータ型の分類とは別に内部メモリーモードがあり，整数型integerと 実数型(倍精度不動小数点型)doubleがあり，それらはtypeof()で確認できる．

(x <- pi)       # 円周率 pi を x に付値

## [1] 3.141593

mode(x)         # モード

## [1] "numeric"

typeof(x)       # タイプ

## [1] "double"

str(x)          # 属性の簡約表示

##  num 3.14

as.integer(x)   # (情報損失が生じる型変換)

## [1] 3

y <- -1
sqrt(y)

## Warning in sqrt(y): 計算結果が NaN になりました

## [1] NaN

sqrt(as.complex(y))  # ---> [1] 0+1i

## [1] 0+1i

データ型には上記の型(原子データ型)とは別にカテゴリデータを扱うfactor()がある．

(f <- factor(c("A","B","A","C","C")))  # 3水準からなる5個のカテゴリカルデータ

## [1] A B A C C
## Levels: A B C

str(f)    # 属性表示

##  Factor w/ 3 levels "A","B","C": 1 2 1 3 3

mode(f)   # モード

## [1] "numeric"

水準“A”,“B”,“C”は内部的には1，2，3で表されている．従ってモードは“numric”である．

R言語には文字列を式(expression)に変換し,R言語として評価する機能がある.

# 文字列を式(expression)に変換する例
(exp1 <- parse(text="x <- 3"))  #　文字列を式(expression)に変換

## expression(x <- 3)

eval(exp1)                      #　式の評価
x                               #　式の評価結果

## [1] 3

str(x)       # 属性

##  num 3

mode(x)      # モード

## [1] "numeric"

is.vector(x) # 型問い合わせ

## [1] TRUE

  Top   PageTop   PageEnd

3 データ構造

R言語には基本的なデータ構造として，ベクトル，行列，配列，データフレーム，リスト が用意されている．R言語には，スカラー はなく，長さ1のベクトルとして表現される．それらのデータ構造は関数str()を用いて確認できる．

  Top   PageTop   PageEnd

3.1 ベクトル

ベクトルの要素は任意の型(logical,numeric,complex,character)でよいが，同一の型でなければならない．スカラーは長さ1のベクトルで表す．

3.1.1 ベクトルの生成

(v <- c(1,2.0,pi,4))       # 要素で定義されたベクトル

## [1] 1.000000 2.000000 3.141593 4.000000

(v <- 1:3)                 # 1から3までの並び seq(3)と同じ

## [1] 1 2 3

(v <- rep("a",3))          # "a" を3個並べたベクトル

## [1] "a" "a" "a"

(v <- seq(0, 5, by=2))     # 初期値0,増分2,終値5以下のベクトル

## [1] 0 2 4

(v <- seq(0, 5, length=3)) # 初期値0,終値5,長さ3のベクトル

## [1] 0.0 2.5 5.0

(v <- seq(3))

## [1] 1 2 3

(v <- c(1, 2.0, pi, 4)); (ind <- seq(along=v)) # ベクトルvに添ったベクトルを生成

## [1] 1.000000 2.000000 3.141593 4.000000

## [1] 1 2 3 4

(v <- sequence(3:1))       # seq(3),  seq(2), seq(1) を並べたベクトルを返す

## [1] 1 2 3 1 2 1

3.1.2 ベクトルの属性

(v <- c(1,2,3))

## [1] 1 2 3

length(v)

## [1] 3

str(v)

##  num [1:3] 1 2 3

v[4] <- 1 + 2i   # べクロルvの全要素がcomplexに統一される
v

## [1] 1+0i 2+0i 3+0i 1+2i

v[5] <- "a"       # べクロルvの全要素がchacterに統一される
v

## [1] "1+0i" "2+0i" "3+0i" "1+2i" "a"

# 型の規則: logical < numeric < complex < character

3.1.3 ベクトルの一部を取り出す

x <- 11:20
x[2:5]                       # x[2], x[3], ..., x[5] を取り出す，x[c(2,3,4,5)] でも良い

## [1] 12 13 14 15

x[-(2:5)]                    # x[2], x[3], ..., x[5] 以外を取り出す

## [1] 11 16 17 18 19 20

x[c(-2,-3,-4,-5)]            # 同上

## [1] 11 16 17 18 19 20

head(x); head(x,n=3)         # 既定では最初の6要素, 3要素

## [1] 11 12 13 14 15 16

## [1] 11 12 13

tail(x, n=3)                 # 最初の3要素

## [1] 18 19 20

3.1.4 ベクトルの一部を置き換える

x <- 1:10;  y <- c(2,5,10);  z <- c(12,15,20)
(w <- replace(x,y,z))        # x の y 中の添字に相当する箇所を z の要素で順に置き換える

##  [1]  1 12  3  4 15  6  7  8  9 20

(w <- replace(x,y,NA))       # 上記zの代わりにNAで置き換える

##  [1]  1 NA  3  4 NA  6  7  8  9 NA

(replace(w,which(is.na(w)),0)) # wの中のNAを0で置き換える

##  [1] 1 0 3 4 0 6 7 8 9 0

3.1.5 ベクトルの要素がある条件を満たすような添字を取り出す

x <- c(0.1, 0.7, 0.2, 0.6, 0.3)
(y <- which(x < 0.5))  # 0.5 未満以の値を持つ要素の添字を取り出す

## [1] 1 3 5

x[y]                 # 0.5 未満以の値を持つ要素を取り出す，x[x < 0.5] と同じ

## [1] 0.1 0.2 0.3

#注意！　xにNAが入っているとx[x < 0.5] とx[which(x < 0.5)]は異なる．
x <- c(-Inf,1,2,3,NA,NaN,5,6, Inf)
x[x<4]               # 結果に注意

## [1] -Inf    1    2    3   NA   NA

x[which(x<5)]        # 結果に注意

## [1] -Inf    1    2    3

  Top   PageTop   PageEnd

3.2 行列

R言語では，データ構造としての“行列”は“ベクトルに次元属性dim()を付加したデータ構造”を意味する．従ってベクトルのデータ構造(すべての要素は同じ型である)はそのまま引き継がれる．

# M <- matrix(1:12, nrow=i, ncol=j, byrow=FALSE, dirnames=z) # 一般形
#    注：x の長さが行列のサイズに足りないと，最初からりサイクル使用される
# M <- matrix(1:12, nrow=3, ncol=4)
# M <- matrix(1:12, nrow=3)              # 自動的に ncol=4 とされる
# M <- matrix(1:12, ncol=4)              # 自動的に nrow=3 とされる
# M <- matrix(1:12, 3, 4)
# M <- matrix(1:12, nc=4, nr=3, b=F)
         # オプション引数名は(一意的に判別可能な範囲で)省略可能
# 
# M <- array(1:12, c(3,4))               # 行列は length(dim)=2 の行列

3.2.1 行列の生成

(M <- matrix(1:12, 3, 4))              # 既定の byrow=FALSE では要素は列主導で並べられる

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

(M <- matrix(1:12, 3, 4, byrow=TRUE))  # 行主導の並びを指定 

##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

(M <- array(1:12, c(3,4)))             # 要素の並びに注意

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# 注意：array は必ず列主導で要素が並べられる
dim(M)                     # 次元属性の表示

## [1] 3 4

is.matrix(M)               # 行列か?

## [1] TRUE

3.2.2 行列の次数

(A <- matrix(1:12, 3, 4))

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

dim(A)  # 行列の大きさ（次元属性）

## [1] 3 4

nrow(A) # 行数． dim(A)[1] と同じ

## [1] 3

ncol(A) # 列数． dim(A)[2] と同じ

## [1] 4

3.2.3 転置行列, 対角行列

(A <- matrix(1:12, 3, 4))

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

(AT <- t(A))  # 行列Aの転置行列

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9
## [4,]   10   11   12

(D <- diag(1, nrow=3, ncol=3)) # 1をリサイクルして3x3対角(単位)行列を生成 

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

(M <- diag(1:3))               # 対角成分を指定して3x3対角行列を生成

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    2    0
## [3,]    0    0    3

3.2.4 ベクトルと行列の変換

(M1 <- rbind(c(1,2,3), c(4,5,6))) # 行ベクトルをあたえて行列を作る

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

(M2 <- cbind(c(1,2,3),c(4,5,6)))  # 列ベクトルをあたえて行列を作る

##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## [3,]    3    6

(vec <- as.vector(t(M1)))         # 行列のベクトル化: 縦ベクトル t(c(1,2,3,4,5,6)) にする

## [1] 1 2 3 4 5 6

(M <- matrix(1:12, nrow=3, ncol=4)) # 3x4 行列Mを生成

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

(M[1,])    # 第1行を取り出す (ベクトルになる)

## [1]  1  4  7 10

(M[, 4])   # 第4列を取り出す (ベクトルになる) 

## [1] 10 11 12

(M[1, , drop=FALSE])   # 第1行を取り出す (1x4 行列になる)

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10

(M[, 4, drop=FALSE])   # 第4列を取り出す (3x1 行列になる)

##      [,1]
## [1,]   10
## [2,]   11
## [3,]   12

3.2.5 ベクトル,行列,データフレーム

M <- 1:6　　　　　　　　　　　　　　　　  #　ベクトルMを生成
str(M)

##  int [1:6] 1 2 3 4 5 6

dim(M) <- c(2,3)　　　　　　　　　　　　#　オブジェクトMに次元属性を付加する
str(M)

##  int [1:2, 1:3] 1 2 3 4 5 6

M　　　　　　　　　　　　　　　　　　　　　#　オブジェクトMを表示

##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6

is.matrix(M)

## [1] TRUE

#　データフレームを行列に変換する
df <- data.frame(vx = 1:4, vy = rnorm(4), vz=c("A","B","B","A")) # データフレームdfを生成
df                                 # df の表示

##   vx         vy vz
## 1  1 -0.2528481  A
## 2  2 -0.4530907  B
## 3  3 -0.1379086  B
## 4  4  0.6053628  A

str(df)                            # df の属性表示

## 'data.frame':    4 obs. of  3 variables:
##  $ vx: int  1 2 3 4
##  $ vy: num  -0.253 -0.453 -0.138 0.605
##  $ vz: Factor w/ 2 levels "A","B": 1 2 2 1

df$vz                              # df の変量vzを表示

## [1] A B B A
## Levels: A B

as.matrix(df)　　　                 #　各要素は文字型に統一されている!!

##      vx  vy           vz 
## [1,] "1" "-0.2528481" "A"
## [2,] "2" "-0.4530907" "B"
## [3,] "3" "-0.1379086" "B"
## [4,] "4" " 0.6053628" "A"

• R言語では,行ベクトル,列ベクトルの区別はされず,長さ(length)のみの属性をもつ.
  
• データフレームは多変量データ行列(p変量nケース:nxp行列)に対応する.従って変量(列ベクトル)毎に型を与えることが可能. 行列は次元属性をもったベクトルより同一の型に統一される.

3.2.6 ベクトルと行列の演算(線形代数の拡張定義に注意)

(x <- 1:3)             # ベクトルxの定義

## [1] 1 2 3

(x + 10)               # x + c(10,10,10) の意味 (10+x も同じ) 

## [1] 11 12 13

(x*10)                 # (10*x も同じ)

## [1] 10 20 30

(y <- c(10,20,30))     # ベクトルyの定義

## [1] 10 20 30

(x + y)                # ベクトルxとベクトルyの和

## [1] 11 22 33

(s <- x %*% y)              # 内積 1*10 + 2*20 + 3*30 = 140

##      [,1]
## [1,]  140

str(s); is.matrix(s); dim(s)   # 内積の結果は(1x1)行列として返される

##  num [1, 1] 140

## [1] TRUE

## [1] 1 1

crossprod(x,y)         # ベクトルxとベクトルyの内積

##      [,1]
## [1,]  140

(M <- matrix(1:6, 2, 3, byrow=T)) # 行列Mの定義

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6

(M + 10)               # Mの全要素に10を加えた行列 (10+M も同じ)

##      [,1] [,2] [,3]
## [1,]   11   12   13
## [2,]   14   15   16

(M * 10)               # Mの全要素に10を掛けた行列 (10*M も同じ)

##      [,1] [,2] [,3]
## [1,]   10   20   30
## [2,]   40   50   60

(M %*% x)              # M(2x3) x(3x1) ー> 結果(2x1):長さ2のベクトルを返す

##      [,1]
## [1,]   14
## [2,]   32

[行列演算]
    %*% (積) ,  %o% (外積),  outer (外積),  t (転置), crossprod (内積),  
    solve (逆行列),  det (行列式),  eigen (固有値),  svd (特異値分解)

  Top   PageTop   PageEnd

3.3 配列

R言語では，“ベクトル”を基本として，長さ1のベクトルで“スカラー”を表し，ベクトルに次元属性を付加することで，“行列(2次元配列)”を定めた．同様に次元属性dim()によって多次元の配列を定めることができる．従ってベクトルのデータ構造(すべての要素は同じ型である)はそのまま引き継がれる．

(A <- array(1:12, dim=c(2,3,2)))  # 3次元配列Aの定義

## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12

A[1,2,2]                          # 要素の表示

## [1] 9

A[,,1]

##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6

is.matrix(A[,,1])

## [1] TRUE

  Top   PageTop   PageEnd

3.4 データフレーム

リスト型に各要素が“同じ長さをもつベクトルである”制約を与えたデータ構造をもつ． あるいは，行列型において“各列ベクトルは同じ型である”制約を外したデータ構造をもつ． 統計でのカテゴリカル(要因)データを含む多変量データ行列をイメージしたデータ構造である． ```

echo ' a  1  2 yes    
 b  2  3  no
 c  5  7 yes
' >  /tmp/tmp.data
cat /tmp/tmp.data

##  a  1  2 yes    
##  b  2  3  no
##  c  5  7 yes

# ●  列ラベル(変数名)の無いデータファイル: /tmp/tmp.data を作成
x <- read.table("/tmp/tmp.data")  # 既定の header=FALSE で読み込み
x            # 第1列:1,2,3はケース番号,第1行:V1,V2,V3は列ラベル(変数名)で,自動的につけられる

##   V1 V2 V3  V4
## 1  a  1  2 yes
## 2  b  2  3  no
## 3  c  5  7 yes

str(x)       # xはデータフレームとして作成される

## 'data.frame':    3 obs. of  4 variables:
##  $ V1: Factor w/ 3 levels "a","b","c": 1 2 3
##  $ V2: int  1 2 5
##  $ V3: int  2 3 7
##  $ V4: Factor w/ 2 levels "no","yes": 2 1 2

# ● ベクトルからデータフレームを作る
df <- data.frame(vx = 1:4, vy = rnorm(4), vz=c("A","B","B","A"))
df

##   vx         vy vz
## 1  1 -1.1166455  A
## 2  2  0.1077378  B
## 3  3 -0.4048640  B
## 4  4 -1.1420284  A

str(df)

## 'data.frame':    4 obs. of  3 variables:
##  $ vx: int  1 2 3 4
##  $ vy: num  -1.117 0.108 -0.405 -1.142
##  $ vz: Factor w/ 2 levels "A","B": 1 2 2 1

# ●  数値行列からデータフレームを作る
M <- matrix(1:12, nrow=4)   # (4x3)表列Mを作成
(df <- data.frame(M))

##   X1 X2 X3
## 1  1  5  9
## 2  2  6 10
## 3  3  7 11
## 4  4  8 12

str(df)

## 'data.frame':    4 obs. of  3 variables:
##  $ X1: int  1 2 3 4
##  $ X2: int  5 6 7 8
##  $ X3: int  9 10 11 12

  Top   PageTop   PageEnd

3.5 リスト

リストの要素は同一の型でなくても良い．

Lst <- as.list(NA)  # リストオブジェクト Lst の初期化
Lst <- list(sex=c(1,2),name=c("Tarou","Hanako"))
Lst

## $sex
## [1] 1 2
## 
## $name
## [1] "Tarou"  "Hanako"

Lst[[1]]　　　 　　#　リストの要素へのアクセスは[[]]を用いる

## [1] 1 2

Lst[["sex"]]　    #　リストの要素を要素名でアクセスする

## [1] 1 2

Lst$sex　　　　 　　#　上記と同じアクセス($演算子を用いる)　<--- 便利

## [1] 1 2

x <- list(vec=1:3, mat=matrix(1:4,c(2,2)),char=c("a","b"))
str(x)

## List of 3
##  $ vec : int [1:3] 1 2 3
##  $ mat : int [1:2, 1:2] 1 2 3 4
##  $ char: chr [1:2] "a" "b"

(v <- unlist(x))        # リストのベクトル化

##  vec1  vec2  vec3  mat1  mat2  mat3  mat4 char1 char2 
##   "1"   "2"   "3"   "1"   "2"   "3"   "4"   "a"   "b"

v[2]

## vec2 
##  "2"

str(v)

##  Named chr [1:9] "1" "2" "3" "1" "2" "3" "4" "a" "b"
##  - attr(*, "names")= chr [1:9] "vec1" "vec2" "vec3" "mat1" ...

リストの直接的な生成

Lst <- as.list(NULL)  # リスト Lst の初期化
Lst[[2]] <- c(21,22)  # リスト Lst の第2要素に代入
Lst

## [[1]]
## NULL
## 
## [[2]]
## [1] 21 22

  Top   PageTop   PageEnd

3.6 文字列

#　cat("a=",a,"b=",b,"\n")  : 文字列の表示
#  nchar() : 文字数
#　grep() : 文字列の検索
#　match(), pmatch() : 文字列の(部分)一致による検索
#　sub(),gsub() : 文字列の(部分)置換
#　substring() : 部分文字列の置換，抽出
#　paste() : 文字列の結合
#　strsplit()　:　文字列の分解
#　toupper(), tolower() : 文字列の大文字・小文字変換
##　parse()　:　文字列を式(expression)に変換
##　deparse()　:　式(expression)を文字列に変換
##   ---> call(), do.call(), quate(), eval(), expression()
a <- 1; b <- 2;  cat("a=",a,"b=",b,"\n") 

## a= 1 b= 2

a <- "abcd"; nchar(a)                 # 文字数

## [1] 4

grep("cd",c("abcd","bcd","cd","d"),value=T)  # 一致した要素を返す

## [1] "abcd" "bcd"  "cd"

grep("cd",c("abcd","bcd","cd","d"))   # 一致した要素番号を返す

## [1] 1 2 3

match("cd",c("abcd","bcd","cd","d"))  #---> [1] 3

## [1] 3

pmatch("cd",c("abcd","bcd","cd","d")) #---> [1] 3

## [1] 3

sub("cd","zz","abcd")                 #---> [1] "abzz"

## [1] "abzz"

file <- paste("file-",1:3,".txt",sep=""); file  # 結果は文字列ベクトル

## [1] "file-1.txt" "file-2.txt" "file-3.txt"

strsplit("This is a pen.", " ")                 # 結果はリスト

## [[1]]
## [1] "This" "is"   "a"    "pen."

(v <- unlist(strsplit("This is a pen.", " ")))  # 結果はベクトル

## [1] "This" "is"   "a"    "pen."

(v <- toString(v))                              # 結果は文字列

## [1] "This, is, a, pen."

(v <- gsub(",","",v))                           # ","を削除

## [1] "This is a pen."

toupper("This is a pen.")        # 大文字化

## [1] "THIS IS A PEN."

tolower("This is a pen.")        # 小文字化

## [1] "this is a pen."

(exp <- parse(text="x <- 3"))    # 文字列のスクリプト化

## expression(x <- 3)

(eval(exp))                      # スクリプトの評価

## [1] 3

3.6.1 文字列操作例

###### 参考 ########################################################################
##
### grep:検索 strsplit:分割 gsub(old,new,line):置換 paste:結合 unlist:リストの解除
#### gsub(",","",toString(v)) # 文字列ベクトルを文字列(スカラー)に変換する
#href <- grep("href=", w0, value=T);   href <- unlist(strsplit(href,"="))[2]
#alt <- grep("alt=", w0, value=T);   alt <- unlist(strsplit(alt,"="))[2]
#htitle <- grep("title=",w0, value=T); htitle <- unlist(strsplit(htitle,"="))[2]
#src <- grep("src=", w0, value=T);     src <- unlist(strsplit(src,"="))[2]
#width <- grep("width=", w0, value=T); width <- unlist(strsplit(width,"="))[2]
#   cat("href=",href,", alt=", alt, ", htitle=",htitle,", 
#        src=",src,",width=",width,"\n")
#  t0 <- grep("<br>", w0, value=T)
#  t1 <- gsub("<br>","",t0)
#  cat("t0=",t0,", length(t0)=",length(t0),", nchar(t0)=",nchar(t0),"\n")
#  cat("t1=",t1,", length(t1=)",length(t1),", nchar(t1)=",nchar(t1),"\n")
#  t1 <- toString(t1)  # 文字列ベクトルを文字列(スカラー)に変換する
#  t1 <- gsub(",","",t1) 
#  cat("toString: t1=",t1,", length(t1=)",length(t1),", nchar(t1)=",nchar(t1),"\n")
#  title <- paste("title: ",t1,sep="",collapse="")
#  cat(title,"\n")
#  title <- t1
#date <- grep("(?:\\d){4}\\.(?:\\d){2}\\.(?:\\d){2}", w0, value=T)  # 2017.04.14
#time <- grep("(?:\\d){1,2}:(?:\\d){2}", w0, value=T)               # 7:07 or 12:05
####################################################################################
(str <- "This is a pen.")

## [1] "This is a pen."

(lst <- strsplit(str," "))   # リストを返す

## [[1]]
## [1] "This" "is"   "a"    "pen."

(v <- unlist(lst))           # ベクトル化

## [1] "This" "is"   "a"    "pen."

toString(v)                  # 文字列化

## [1] "This, is, a, pen."

gsub(",","",toString(v))     # 文字列strに復元

## [1] "This is a pen."

(v1 <- paste("paste vector: ",v,sep=""))  # 注意:ベクトルをpasteすると...

## [1] "paste vector: This" "paste vector: is"   "paste vector: a"   
## [4] "paste vector: pen."

paste("paste str: ",gsub(",","",toString(v)),sep="")

## [1] "paste str: This is a pen."

3.6.2 文字列の検索と置換

# example(grep)
# example(regexpr)
line <- paste('<span style="display:inline-block:font-size:85%">\n',
              ' <a href="/var/www/html/OI000123.jpg" rel="lightbox1" alt="No.4" \n',
              '  title="No4 日本橋>" \n',
              ' <img src="/var/www/html/OI000123.jpg" width="160" border="0"> \n',
              ' </a> <br>日本橋:日本国道路元標<br> 2017.04.14 &nbsp; 5:43 \n </span>')
line

## [1] "<span style=\"display:inline-block:font-size:85%\">\n  <a href=\"/var/www/html/OI000123.jpg\" rel=\"lightbox1\" alt=\"No.4\" \n   title=\"No4 日本橋>\" \n  <img src=\"/var/www/html/OI000123.jpg\" width=\"160\" border=\"0\"> \n  </a> <br>日本橋:日本国道路元標<br> 2017.04.14 &nbsp; 5:43 \n </span>"

# grep("href",line)
# grep("href", line, value=T)
# regexpr("href",line)
nchar(line)

## [1] 262

(w0 <- unlist(strsplit(line," ")))

##  [1] "<span"                                          
##  [2] "style=\"display:inline-block:font-size:85%\">\n"
##  [3] ""                                               
##  [4] "<a"                                             
##  [5] "href=\"/var/www/html/OI000123.jpg\""            
##  [6] "rel=\"lightbox1\""                              
##  [7] "alt=\"No.4\""                                   
##  [8] "\n"                                             
##  [9] ""                                               
## [10] ""                                               
## [11] "title=\"No4"                                    
## [12] "日本橋>\""                                      
## [13] "\n"                                             
## [14] ""                                               
## [15] "<img"                                           
## [16] "src=\"/var/www/html/OI000123.jpg\""             
## [17] "width=\"160\""                                  
## [18] "border=\"0\">"                                  
## [19] "\n"                                             
## [20] ""                                               
## [21] "</a>"                                           
## [22] "<br>日本橋:日本国道路元標<br>"                  
## [23] "2017.04.14"                                     
## [24] "&nbsp;"                                         
## [25] "5:43"                                           
## [26] "\n"                                             
## [27] "</span>"

grep("href=",w0)

## [1] 5

(w1 <- grep("href=",w0,value=T))

## [1] "href=\"/var/www/html/OI000123.jpg\""

(w2 <- gsub("href=","",w1))

## [1] "\"/var/www/html/OI000123.jpg\""

str(w2)

##  chr "\"/var/www/html/OI000123.jpg\""

(w1 <- grep("src=",w0,value=T))

## [1] "src=\"/var/www/html/OI000123.jpg\""

(w2 <- gsub("src=","",w1))

## [1] "\"/var/www/html/OI000123.jpg\""

str(w2)

##  chr "\"/var/www/html/OI000123.jpg\""

(w1 <- grep("<br>",w0,value=T))

## [1] "<br>日本橋:日本国道路元標<br>"

(w1 <- grep("(?:\\d){4}\\.(?:\\d){2}\\.(?:\\d){2}",w0,value=T))  # 2017.04.14

## [1] "2017.04.14"

(w1 <- grep("(?:\\d){1,2}:(?:\\d){2}",w0,value=T))               # 7:07 or 12:05

## [1] "5:43"

(sw1 <- grep("href=",w0,value=T))

## [1] "href=\"/var/www/html/OI000123.jpg\""

length(sw1)

## [1] 1

(fname <- unlist(strsplit(sw1,"="))[2])

## [1] "\"/var/www/html/OI000123.jpg\""

if (length(sw1)==0) {cat("sw1=",sw1, " ---> not found\n")}
(sw2 <- grep("hrf=",w0,value=T))

## character(0)

if (length(sw2)==0) {cat("sw2=",sw2, "---> not found\n")}

## sw2=  ---> not found

  Top   PageTop   PageEnd

3.7 属性の変換 as.??? 判定 is.???

as.??? は属性の変換， is.??? は属性の判定をおこなう． * は両機能をもつ．

  * as.array         * as.call      * as.character     * as.complex
  * as.data.frame
       as.data.frame.AsIs, as.data.frame.Date, as.data.frame.array,
       as.data.frame.character, as.data.frame.complex, as.data.frame.data.frame
       as.data.frame.default, as.data.frame.factor, as.data.frame.integer 
       as.data.frame.list, as.data.frame.logical, as.data.frame.matrix
       as.data.frame.model.matrix, as.data.frame.numeric, 
       as.data.frame.ordered, as.data.frame.package_version, 
       as.data.frame.table, as.data.frame.ts, as.data.frame.vector
  * as.double        is.element    * as.environment   * as.expression
  * as.factor      * as.function   * as.integer
  * as.list
       as.list.data.frame, as.list.default, as.list.environment
  * as.logical
  * as.matrix
     as.matrix.data.frame, as.matrix.default, as.matrix.noquote
  * as.name        * as.null    * as.numeric     * as.ordered
  * as.package_version          * as.pairlist    * as.qr
    as.raw         * as.real    * as.single      * as.symbol   
  * as.table       * as.vector    as.vector.factor

  Top   PageTop   PageEnd

4 R言語の主な 組込み関数

4.1 組込み関数

● 基本的な組込み関数(符号，絶対値，平方根)
    * sign(x) 実数 x の符号．x > 0, = 0, x <0 に応じて sign(x) = -1,0,1
    * abs(x) 実数もしくは複素数 x の絶対値
    * sqrt(x) 整数の平方根，もしくは複素数の平方根(主値)
● 三角関数ファミリー(引数の単位はラディアンでベクトル化されている)
   cos(x)  sin(x)  tan(x)  acos(x)   asin(x)  atan(x)   atan2(y, x)
● hyperbolic 関数ファミリー  [cosh(x) = (exp(x) + exp(-x))/2]
   cosh(x)  sinh(x)  tanh(x)   acosh(x)  asinh(x)  atanh(x)   
● 対数，指数関数ファミリー(底 base は実数．引数 x は実数もしくは複素数)
   log(x, base = exp(1))   底 base (既定値 exp(1)) の対数
   log10(x)        常用対数 log(x, base=10)
   log2(x)         底 2 の対数
   exp(x)          指数関数
● 組合せ論的関数
    * choose(n, k) n 個から k 個を取り出す場合の数
    * lchoose(n, k) choose(n,k) の自然対数
    * factorial(x) x の階乗 x! (R 1.9 より登場．実際は単に gamma(x+1) を
      計算するだけで，整数でない x も可能)
● 数値ベクトルに対する逐次処理関数
    * cumsum(x) 累積和ベクトルを返す
    * cumprod(x) 逐次積ベクトルを返す
    * cummax(x) 逐次最大値ベクトルを返す
    * cummin(x) 逐次最小値ベクトルを返す
●  ガンマ関数ファミリー
    * beta(a, b)．ベータ関数 B(a,b) = (gamma(a)gamma(b))/(gamma(a+b))．
      引数 a,b は零および負整数を除く数値(のベクトル)．
    * lbeta(a, b)．ベータ関数の自然対数．直接計算しており，
      log(beta(a, b)) として計算しているわけではない．
    * gamma(x)．ガンマ関数．引数 x は零および負整数を除く数値(のベクトル)．
      正の整数 n に対する階乗 n! は gamma(n+1) として計算するのが基本．
    * lgamma(x)．ガンマ関数の自然対数．直接計算しており，log(gamma(x)) として計算しているわけではない．
    * digamma(x)．lgamma の一階微分．    * trigamma(x)．lgamma の二階微分．
    * tetragamma(x)．lgamma の三階微分． * pentagamma(x)．lgamma の四階微分．
    * choose(n, k)．二項係数(n 個から k 個を選ぶ場合の数)．gamma(n+1)/(gamma(k+1)gamma(n-k+1)) として計算して
      いるので n, k が整数でなくても値は得られるが，結果は整数化されるようである(そもそも意味はなさそうであるが)．
    * lchoose(n, k)．二項係数 choose(n,k) の自然対数．直接計算しており，
      log(choose(n,k)) として計算しているわけではない．
---> 確率分布関数は hlp("dist") を，統計関数は hlp("rstat") を参照

sin(0)               # sin(0) [ラジアン]

## [1] 0

sin((0:6)*pi/6)      # 0, π/6, 2π/6, 3π/6, 4π/6, 6π/6, 6π/6=π におけsin値

## [1] 0.000000e+00 5.000000e-01 8.660254e-01 1.000000e+00 8.660254e-01
## [6] 5.000000e-01 1.224647e-16

exp(1)               # 自然対数の底

## [1] 2.718282

log(c(0,1,exp(1)))    # 自然対数

## [1] -Inf    0    1

log(c(0,1,2,4,8),base=2)   # 底が2の対数

## [1] -Inf    0    1    2    3

log2(c(0,1,2,4,8))         # 底が2の対数

## [1] -Inf    0    1    2    3

choose(3,1)                # 3個から1個を取り出す場合の数

## [1] 3

factorial(3)               # 階乗 3!

## [1] 6

gamma(4)                   # ガンマ関数 Γ(n) = (n-1)! (n: positive integer)

## [1] 6

cumsum(c(0.2, 0.3, 0.4, 0.1))  # 累積和ベクトルを返す

## [1] 0.2 0.5 0.9 1.0

cummax(c(0.2, 0.3, 0.4, 0.1))  # 逐次最大値ベクトルを返す

## [1] 0.2 0.3 0.4 0.4

  Top   PageTop   PageEnd

4.2 オーダー，ソート，ランク

 > x <- c(20,40,30,10) ; x ---> [1] 20 40 30 10
 > ox <- order(x)           # 昇順順位のデータ位置(添字)を返す
 > ox ---> [1] 4 1 3 2      # (第1順位のデータ位置は4である．．．)
 > x[ox] ---> [1] 10 20 30 40   # 昇順にソートされた結果を返す

逆順に並べ変えるには
 > rox <- rev(order(x));  rox ---> [1] 2 3 1 4
 > x[rox]                     ---> [1] 40 30 20 10

[参考] > sort(x)   ---> [1] 10 20 30 40  # 昇順に並び換えた結果を返す
       > rank(x)   ---> [1] 2 4 3 1      # 昇順順位を返す(1番目のデータは第2順位)
長さの等しい二つのベクトル x,y を x の大小順にプロット
 > oo<-order(x); plot(x[oo],y[oo],type="l")

x <- c(20,40,30,10)   # 4個のデータの並びを(ベクトル)xとする
sort(x)               # 昇順に並び換えた結果を返す

## [1] 10 20 30 40

order(x)              # 昇順順位の個体番号（データ位置）を返す

## [1] 4 1 3 2

                      #     (第1順位データは4番目)
rank(x)               # 個体番号の昇順順位を返す(20は第2順位である)

## [1] 2 4 3 1

x[c(1,3)]             # x から1番目と3番めのデータを取り出す

## [1] 20 30

ox <- order(x); x[ox] # ox を添字ベクトルとするデータ(間接指定)

## [1] 10 20 30 40

rev(x)                # xを逆順に並べた結果

## [1] 10 30 40 20

  Top   PageTop   PageEnd

4.3 基本統計関数

多くの場合，総称関数として作用し，多変量データ，時系列データにも使える．
  * max(..., na.rm=FALSE)       最大値
  * min(..., na.rm=FALSE)       最小値
  * range(..., na.rm = FALSE)   範囲
  * mean(x, ...)                平均
  * weighted.mean(x, w)         重み付平均
  * median(x, na.rm=FALSE)      メディアン(中央値)
  * quantile(x, probs = seq(0, 1, 0.25),na.rm =FALSE, ...)    パーセント点
  * fivenum(x, na.rm = TRUE)    Tukey統計値
  * IQR(x)                      四分位範囲(Interquartile Range)
  * mad(x)                      中央値絶対偏差(median absolute deviation)
  * var(x, y = NULL)            分散(不偏分散)  共分散も可

  * sd(x, na.rm = FALSE)        標準偏差
  * cor(x, y = NULL)            相関係数
  * cov(x, y = NULL)            共分散

  * table(x)                    集計表
  * cut(x,breaks,right=T)       度数集計

  * sum(x)                      総和
  * prod(x)                     総積
  * cumsum(x)                   累積和

  * rowSums  rowMeans           各行ごとの和   行ごとの平均
  * colSums  colMeans           各列ごとの和   列ごとの平均

  * diff(x, lag=1, dfference=1, ...)   階差

  * scale(X)                           標準化変換(平均，標準偏差による) 
  * scale(X,scale=F)                   平均を原点とする変換

x <- c(10,20,30)         # 3個のデータをベクトルxとする
min(x); max(x)           # 最小値，最大値を求める

## [1] 10

## [1] 30

mean(x); var(x); sd(x)   # 平均，分散(不偏分散)，標準偏差を求める

## [1] 20

## [1] 100

## [1] 10

(z <- scale(x))          # 平均と標準偏差に基づく標準化変換を行う

##      [,1]
## [1,]   -1
## [2,]    0
## [3,]    1
## attr(,"scaled:center")
## [1] 20
## attr(,"scaled:scale")
## [1] 10

  Top   PageTop   PageEnd

4.4 確率分布

    dist : 指定できる分布
    (d***：確率密度，p***：分布関数値，q***：パーセント点，r***：乱数)
    2項：binom(x,n,p),              ポアソン：pois(x,lam)，
    負の2項：nbinom(x,n,p)          幾何：geom(x,p)，    
    超幾何 : hyper(x,m,n,k)，       *離散一様: DU(x,x0,dx,x1)
    一様：unif(x,a,b)，             指数：exp(x,lam)，
    正規：norm(x,mu,sd),            コーシー：cauchy(x,mu,s)， 
    ガンマ：gamma(x,a,rate=1/s)，   ベータ：beta(x,a,b)，
    対数正規：lnorm(x,mu,sigma)，   ワイブル：weibull(x,shape,scale=1)，
    ロジスティック：logis(x,loc=0,scale=1)，
    t：t(x,df,ncp=0)，              カイ2乗：chisq(x,df,ncp=0)，
    F：f(x,df1,df2),                
    *混合正規分布:normmix(x.mu1,sd1,mu2,sd2,p)
    *2変量正規分布：dnorm2(x,y,means=c(0,0),sds=c(1,1),cor=0)
    *多変量正規分布に従う乱数生成 : mk.mvd(n,av,sd,R,seed=1,round=F)

4.4.1 正規分布と正規乱数

options(width=60,dights=4)
dnorm(0,0,1)   # 正規分布N(0,1^2)の0における確率密度

## [1] 0.3989423

pnorm(0,0,1)   # 正規分布N(0,1^2)の0における分布関数値(P{X < 0})

## [1] 0.5

1 - pnorm(c(0,1,2,3),0,1)   # 上側確率 P{X > x}

## [1] 0.500000000 0.158655254 0.022750132 0.001349898

c(1/2, 1/6, 1/44, 1/1000)   # 上記の上側確率に近い分数 

## [1] 0.50000000 0.16666667 0.02272727 0.00100000

qnorm(0.5,0,1) # 正規分布N(0,1^2)の50%点(P{X < x0}=0.5 となるx0の値)

## [1] 0

rnorm(10,0,1)  # 正規分布N(0,1^2)に従う確率変数の実現値(正規乱数)を10個生成

##  [1]  0.52527622  0.83637721 -0.23742394  0.88677093
##  [5] -0.04510166 -0.56370324 -0.26841459 -0.04175261
##  [9] -0.42558117 -1.44082874

set.seed(1)                  # 乱数の初期値を設定
x <- rnorm(10000,0,1)        # N(0,1^2)に従う乱数を10000個生成する
out <- hist(x,freq=F,xlim=c(-4,4))  # データxのヒストグラムを作成描画する 
par(new=T)                   # 図を上書きする
dens <- function(x){dnorm(x,mean=0,sd=1)} 
   # N(0,1^2)の密度関数を関数densとする(dnormは3変数関数であるため)
curve(dens,xlim=c(-4,4),col="red",add=T) # 関数densを上書き描画する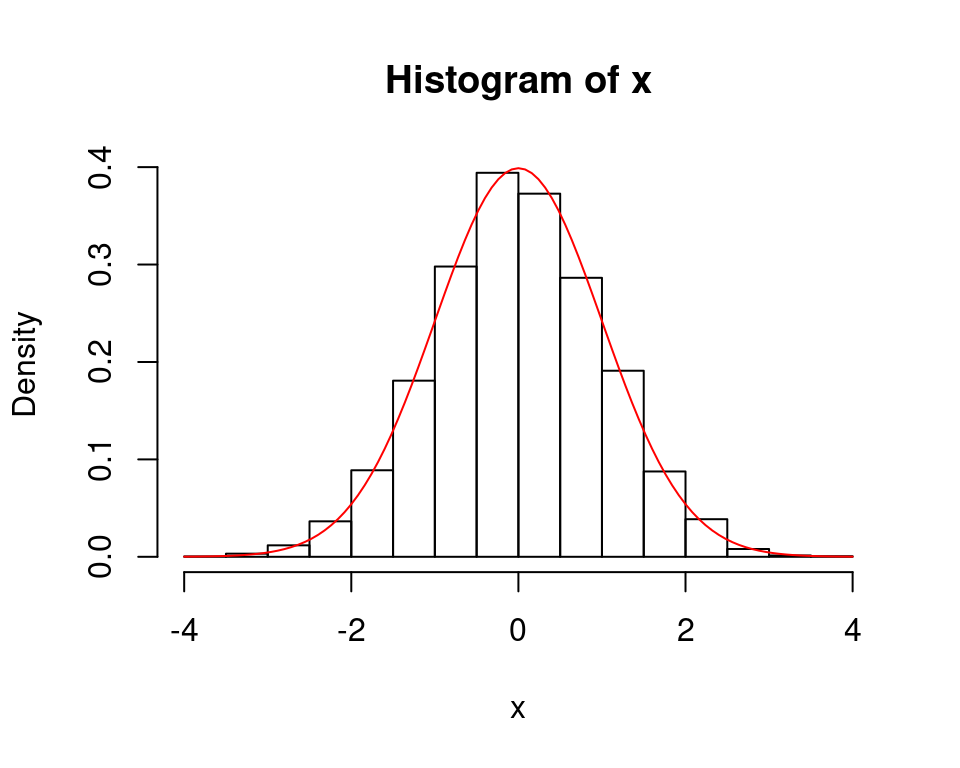

out      # ヒストグラム(度数分布表)の詳細

## $breaks
##  [1] -4.0 -3.5 -3.0 -2.5 -2.0 -1.5 -1.0 -0.5  0.0  0.5  1.0
## [12]  1.5  2.0  2.5  3.0  3.5  4.0
## 
## $counts
##  [1]    2   16   59  182  444  904 1490 1971 1864 1432  955
## [12]  438  193   40    7    3
## 
## $density
##  [1] 0.0004 0.0032 0.0118 0.0364 0.0888 0.1808 0.2980 0.3942
##  [9] 0.3728 0.2864 0.1910 0.0876 0.0386 0.0080 0.0014 0.0006
## 
## $mids
##  [1] -3.75 -3.25 -2.75 -2.25 -1.75 -1.25 -0.75 -0.25  0.25
## [10]  0.75  1.25  1.75  2.25  2.75  3.25  3.75
## 
## $xname
## [1] "x"
## 
## $equidist
## [1] TRUE
## 
## attr(,"class")
## [1] "histogram"

正規分布 \(X \sim N(\mu,\,\sigma^2)\) の確率密度関数\(f(x)\): \[ f(x) = \frac{1}{\sqrt{2\,\pi\,\sigma^2}}\,e^{-\,\dfrac{(x-\mu)^2}{2\, \sigma^2}}\]

  Top   PageTop   PageEnd

5 R言語のプログラム機能

5.1 論理値演算

==, !=      等しい, 等しくない
<, <=       小さい, 小さいか等しい
>, >=       大きい, 大きいか等しい
!           否定
&, &&       論理積(要素ごとの演算を行い結果は論理ベクトル), (結果は論理値)
|, ||       論理和(要素ごとの演算を行い結果は論理ベクトル), (結果は論理値)
xor()       排他的論理和(要素ごとの演算を行い結果は論理ベクトル)

2 < 3

## [1] TRUE

-2 < -3

## [1] FALSE

(2 < 3) & (-2 < -3)

## [1] FALSE

(2 < 3) && (-2 < -3)

## [1] FALSE

cat("論理積: F&F=",FALSE&FALSE,", F&T=",FALSE&TRUE,
         ", T&F=",TRUE&FALSE,", T&T=",TRUE&TRUE,"\n")

## 論理積: F&F= FALSE , F&T= FALSE , T&F= FALSE , T&T= TRUE

cat("論理和: F|F=",FALSE | FALSE,", F|T=",FALSE | TRUE,
         ", T|F=",TRUE | FALSE,", T|T=",TRUE | TRUE,"\n")

## 論理和: F|F= FALSE , F|T= TRUE , T|F= TRUE , T|T= TRUE

cat("排他的論理和: xor(F,F)=",xor(FALSE,FALSE),", xor(F,T)=",xor(FALSE,TRUE),
         ", xor(T,F)=",xor(TRUE,FALSE),", xor(T,T)=",xor(TRUE,TRUE),"\n")

## 排他的論理和: xor(F,F)= FALSE , xor(F,T)= TRUE , xor(T,F)= TRUE , xor(T,T)= FALSE

x <- c(FALSE,FALSE,TRUE,TRUE)
y <- c(FALSE,TRUE,FALSE,TRUE)
x & y     # xとyの要素毎の論理積の結果を返す

## [1] FALSE FALSE FALSE  TRUE

x && y    # xの第1要素とyの第1要素の論理積の結果のみを返す(第2要素以降の論理積は評価されない!)

## [1] FALSE

x | y     # xとyの要素毎の論理和の結果を返す

## [1] FALSE  TRUE  TRUE  TRUE

x || y    # xの第1要素とyの第1要素の論理和の結果のみを返す(第2要素以降の論理和は評価されない!)

## [1] FALSE

xor(x,y)  # xとyの要素毎の排他的論理和の結果を返す

## [1] FALSE  TRUE  TRUE FALSE

5.1.1 論理値の計算

FALSE + TRUE + TRUE  

## [1] 2

FALSE + TRUE - TRUE 

## [1] 0

(x <- c(FALSE,TRUE,TRUE))

## [1] FALSE  TRUE  TRUE

x[2] <- 0     # 論理ベクトルの整数値ベクトル化
x

## [1] 0 0 1

x[2] <- 2.5   # 整数値ベクトルの実数値ベクトル化
x

## [1] 0.0 2.5 1.0

x <- c(FALSE,TRUE,TRUE)   # 論理値ベクトル
sum(x)                    # 数値化されて計算される

## [1] 2

5.1.2 論理値関数: all(), any(), which(), which.min(), which.max()

all(v)         すべての要素が条件vを満たすか(vはベクトルに対する条件式か,その論理値ベクトル)
any(v)         どれかの要素が条件vを満たすか
which(v)       条件vを満たす要素番号を返す
which.min(v)   ベクトルvの最小値の要素番号を返す
which.max(v)   ベクトルvの最大値の要素番号を返す

(x <- c(3, 1, 4, 1, 5))   # 数値ベクトル x の定義

## [1] 3 1 4 1 5

(v <- x > 3)              # xの条件x>3に対する論理値ベクトル

## [1] FALSE FALSE  TRUE FALSE  TRUE

all(x > 3)                # すべての要素が条件を満たすか

## [1] FALSE

all(v)                    # 同上

## [1] FALSE

any(x > 3)                # どれかの要素が条件を満たすか

## [1] TRUE

any(v)                    # 同上

## [1] TRUE

which(x > 3)              # 条件を満たす要素は何番目か

## [1] 3 5

which(v)                  # 同上

## [1] 3 5

which.min(x)              # 最小値は何番目か

## [1] 2

which.max(x)              # 最大値は何番目か

## [1] 5

5.1.3 欠損値(NA:Not Avairable)と論理演算

x <- c(NA, 0, 1, 2)
log(x)

## [1]        NA      -Inf 0.0000000 0.6931472

cat("論理積: NA&F=",NA&FALSE,", NA&T=",NA&TRUE,"\n")

## 論理積: NA&F= FALSE , NA&T= NA

cat("論理和: NA|F=",NA | FALSE,", NA|T=",NA | TRUE,"\n")

## 論理和: NA|F= NA , NA|T= TRUE

sum(x)

## [1] NA

sum(x,na.rm=TRUE)

## [1] 3

(y <- na.omit(x))

## [1] 0 1 2
## attr(,"na.action")
## [1] 1
## attr(,"class")
## [1] "omit"

  Top   PageTop   PageEnd

5.2 条件判定

• if(条件式） {式1} else {式2}
• ifelse(条件式, 式1, 式2)
• switch(type, case1, case2, …, “otherwise”)

x <- 3
if (x > 0) {print("x>0")} else {print("x<=0")}

## [1] "x>0"

ifelse(x>0, print("x>0"), print("x<=0"))

## [1] "x>0"

## [1] "x>0"

v <- c(-1, 3)  # 注意
if (v > 0) {print("v>0")} else {print("v<=0")} # 第1要素に対してのみ条件判定が行われる

## Warning in if (v > 0) {: 条件が長さが 2 以上なので、最初の 1
## つだけが使われます

## [1] "v<=0"

ifelse(v > 0, print("v>0"), print("v<=0"))     # 要素毎の条件判定が行われる

## [1] "v>0"
## [1] "v<=0"

## [1] "v<=0" "v>0"

• 注: if文の“} else {”は同一行に記述する習慣を身に着けよ!

# switch文の例
func1 <- function(x, type) {
       switch(type,
                 mean = mean(x),
                 median = median(x),
                 trimmed = mean(x, trim = 0.1), # 両端から10%づつカットした平均
                 "Otherwise"  )   }
x <- c(1,3,5,7,9) 
func1(x, "mean")  #文字列 "mean" にマッチした項目の値 mean(x) が返される

## [1] 5

func1(x, "trimmed")

## [1] 5

func1(x, "Q")

## [1] "Otherwise"

  Top   PageTop   PageEnd

5.3 ループ制御

• repeat{式} 式を繰り返す (break: ループより抜ける, next: 次のループを始める)
  
• while(条件式) {式}
• for (i in v) {式}

# repeat文
i <- 0
repeat{ i <- i + 1
        cat("i=",i,"\n")
        if(i < 3) next; 
        if(i==3) break} # end of repeat

## i= 1 
## i= 2 
## i= 3

i

## [1] 3

# while文
i <- 0
while(i < 3){
   i <- i + 1
   cat("i=", i, "\n")
   } # end of while

## i= 1 
## i= 2 
## i= 3

# for文
for (i in 1:3) {
   cat("i=", i, "\n")
   } # end of for

## i= 1 
## i= 2 
## i= 3

v <- NULL
seq(along=v)

## integer(0)

for (i in seq(along=v)) {  # ベクトルvがNULLの場合も正常に処理される
   cat("i=", i, "\n")
   } # end of for
# 注:ベクトル処理が可能な場合はループ処理は避けること(apply(),lapply()参照)

  Top   PageTop   PageEnd

5.4 apply関数群

• apply() 行列や配列の行ないし列毎に関数を適用する
• lapply() apply()をリスト,データフレーム,ベクトルに適用する
• sapply() lapply()と同じ処理を行うが,簡素化した結果を返す
• mapply() sappy()を多変量データに適用
• tapply() 要因によってグループ化したクロス表を返す

# applyの例
(M <- matrix(c(3, 1, 4, 2, 7, 3), ncol=2))  # (3x2)行列Mを定義

##      [,1] [,2]
## [1,]    3    2
## [2,]    1    7
## [3,]    4    3

apply(M, 1, max)                            # Mの各行(第2引数に1を指定)に関数max()を適用

## [1] 3 7 4

M[,1]                                       # Mの第1列を表示

## [1] 3 1 4

range(M[,1])                                # Mの第1列の範囲区間(min,max)を表示

## [1] 1 4

diff(range(M[,1]))                          # 上記のmax-minを表示

## [1] 3

apply(M, 2, function(x){diff(range(x))} )   # Mの各列(第2引数に2を指定)に無名関数を適用

## [1] 3 5

  Top   PageTop   PageEnd

5.5 関数定義に関して

  ls()            関数を含むオブジェクト一覧を表示
  func            関数名 func の関数の表示
  formals(func)   関数 func の引数の表示
  body(func)      関数 func の本体の表示
  base::log       base パッケージ中の関数 log の情報を得る
 
  func <- function(x,y=NULL,xlim=c(x0,x1),...) { body }
  return(out)
  invisible(list(x=x,y=y))
  [停止] f <- function(x){ifelse(x<=0, stop(message='非負値引数'),log(x))}
  try( func(...) ) <--- エラー回復機能付実行

5.5.1 関数定義

foo <- function(x, y){                        # foo という名前の関数を二つの引数 x, y で定義
    z <- x + y; w <- x * y                    # セミコロンで区切って一行に
    if (z > w) {t <- z}                       # 好みで if (z > w) {t <- z} としても可
       else {t <- w; w <- z; z <-t}           # 波括弧で囲むとブロック化される
    for (i in 1:10) { w <- w + i; z <- z - i}
    cat("z = ", z, " w = ", w, "?n")
    return (list(w=w, z=z))                   # 二つの返り値をリストにまとめて返す
    } # end of foo
foo(2, 3)  # すぐ実行できる

## z =  -49  w =  60 ?n

## $w
## [1] 60
## 
## $z
## [1] -49

func1 <- function(a,b,c){
   cat("2次方程式 a x^2 + b x + c = 0 (a !=0) の実数解を求める\n")
   cat("a =",a,", b =",b, ", c =",c,"\n") 
   D <- b^2 - 4*a*c
   if (D > 0) {
       cat("D =",D, " > 0  --- 2実数解\n")
       x1 <- (-b - sqrt(D))/(2*a) ;  x2 <- (-b + sqrt(D))/(2*a) # セミコロンで区切って一行に
     } else if (D==0) {
       cat("D =",D, " = 0  --- 1実数解\n")
       x1 <- -b/(2*a);   x2 <- NULL
     } else if (D < 0) {
       cat("D =",D, " < 0  --- 0実数解\n")
       x1 <- NULL;      x2 <- NULL
     } else {
       stop("D =",D, " --- 予期しないエラーが発生した.\n")
     } # end of if
   return(list(x1,x2))
   } # end of func1
func1(1,2,3)

## 2次方程式 a x^2 + b x + c = 0 (a !=0) の実数解を求める
## a = 1 , b = 2 , c = 3 
## D = -8  < 0  --- 0実数解

## [[1]]
## NULL
## 
## [[2]]
## NULL

func1(1,2,-3)

## 2次方程式 a x^2 + b x + c = 0 (a !=0) の実数解を求める
## a = 1 , b = 2 , c = -3 
## D = 16  > 0  --- 2実数解

## [[1]]
## [1] -3
## 
## [[2]]
## [1] 1

func1(1,2,0)

## 2次方程式 a x^2 + b x + c = 0 (a !=0) の実数解を求める
## a = 1 , b = 2 , c = 0 
## D = 4  > 0  --- 2実数解

## [[1]]
## [1] -2
## 
## [[2]]
## [1] 0

●名前・既定値つきの引数
* 引数名=既定値 の形式で既定値を指定できる(関数実行時に明示的に引数の値を 指定しないとこの値が使われる)．

digitsBase <- function(x, base = 2, ndigits = 1 + floor(log(max(x), base)))
  { ndigits }
 
digitsBase(10)               # base と ndigits は既定値が使われる

## [1] 4

digitsBase(10, base = 8)     # base と ndigits は既定値が使われる

## [1] 2

digitsBase(10, ndigits = 5)  # base に既定値 2 が使われる

## [1] 5

digitsBase(10, base = 8, ndigits = 5)  # 既定値なし

## [1] 5

●引数として関数オブジェクトを与える場合
引数として関数オブジェクトを与えることができる．普通関数オブジェクト名を引数として与える：

 x <- 0:20/20
 par(mfcol=c(1,3))
 test <- function(x, fun=sin) {plot(x, fun(x))}
 test(x)                               # 既定の関数 sin が使われる
 test(x, fun=cos)                      # 関数として cos が使われる
 test(x, fun=function(z) 1/(1+exp(z))) # 関数定義を直接与える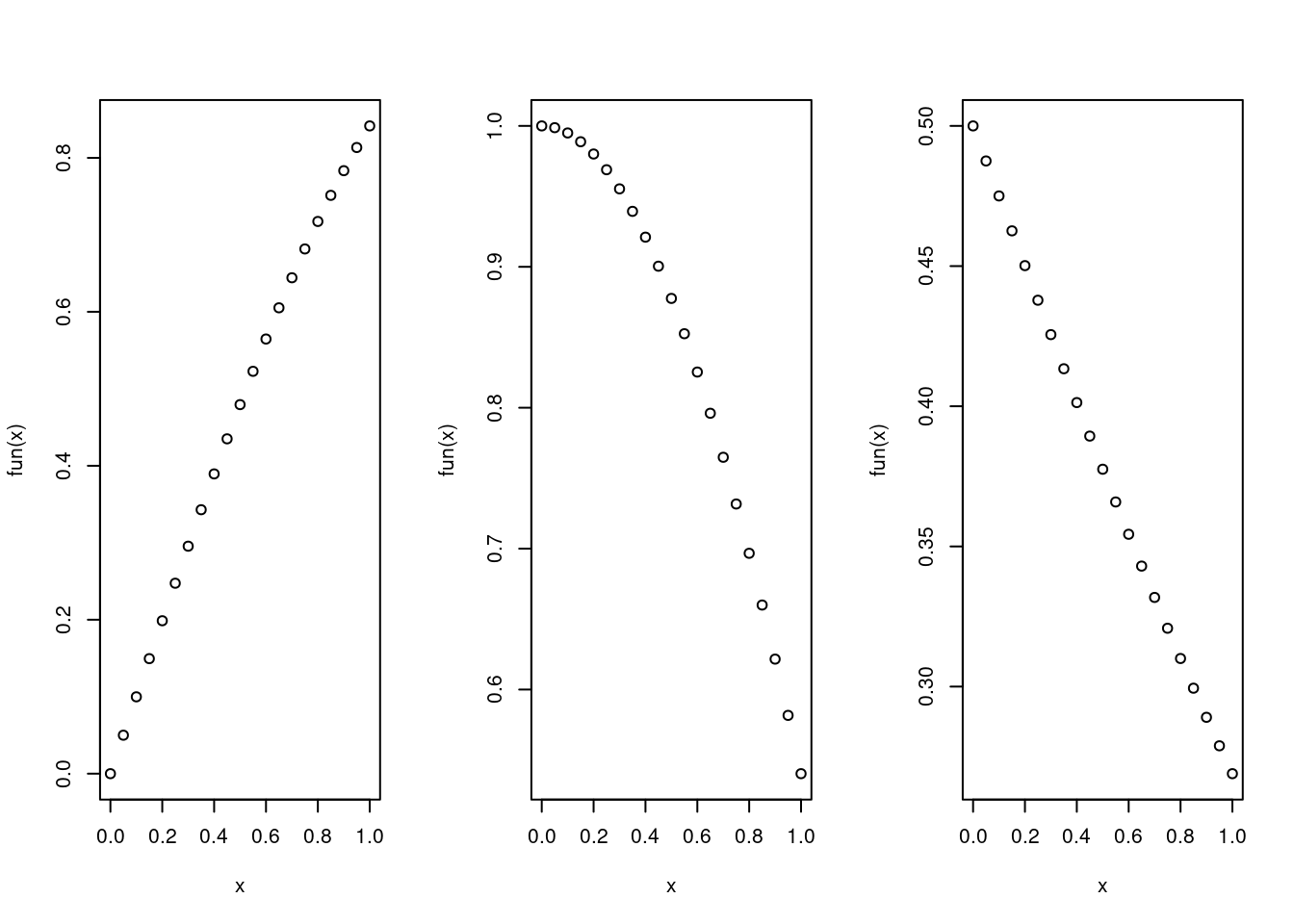

●特別な(その他大勢)引数 …
* 特別な引数として … が使える．これは任意の，そして複数の 追加引数を指定するのに使われる．その内容は例えば …[1], …[2], …, …[length(…)] で取り出せる．しばしば関数内部で呼び出される(グラフィックスや最適化)関数のパラメータの指定に使われている．

foo <- function(x, ...) {
              if (x >= 0) return(x*cos(...[1]) + x^2*sin(...[2]))
              else return(exp(x))}
foo(1,c(2,3))       # ... にベクトル値

## [1] -0.2750268

foo(-1)             # ... 部分の引数無し．実際この場合必要無い

## [1] 0.3678794

* 特殊引数 ... は関数引数欄の最後におかれるのが普通であるが，途中に置くこともできる．その際，実際の呼出しでは，以後の引数は必ず名前つきで与えないとエラーになる．この特徴は面倒のようにも思えるが，...
  引数は実際には不定個数の引数を代表することを考えれば納得が行く．この特徴は逆に引数の与え損ないを防ぐために積極的に使うこともできる．

●暗黙の返り値
もし return(), invisible() 関数により返り値を陽に指定しなければ，(関数本体の最後に実行される表現式が値を返す限り)それが関数の暗黙の返り値とされる.

foo1 <- function (x) x^2   # x^2 の値が暗黙の返り値
foo1(2)

## [1] 4

●返り値関数 return()
* 関数本体に return() を置くとその中身が返り値とされる * return() が複数あっても良いが，いずれかの return() が実行されるとその時点で関数は終了する（呼ばれたところに戻る).

foo <- function (x,y) {return(x+y)}
foo(1,2)    # x+y  が返り値

## [1] 3

foo <- function (x, y) {return(x); cat("sum =", x+y)}
foo(1,2)   # cat は実行されない

## [1] 1

foo <- function (x,y) {if (x>=y) return(x) else return(y)} # max(x,y)を計算
foo(1,2)

## [1] 2

foo(2,1)

## [1] 2

●複数の返り値 return()
* return() 関数の中に，複数の値を置くと，返り値はそれらを順につないだリストになる * リスト成分には名前ラベルを与えることができる * この機能は将来廃止されるらしく，R.1.8 からは警告がでるようになった． 明示的に return( list(x,y,x+y) ) 等としたほうが良さそう．

foo <- function (x,y) {sum <- x+y; return(list(x=x,y=y,sum=x+y))}  # ラベル付き返り値
(res <- foo(1,2))

## $x
## [1] 1
## 
## $y
## [1] 2
## 
## $sum
## [1] 3

res$sum  # res[[3]], res[["sum"]] でも良い

## [1] 3

●コンソールに表示されない返り値 invisible()
例えば，非常に大量で，可読性の低い値を返す関数を考えると，返り値を変数に付値する場合以外コンソールに 出力したくない事が起きる．invisible() はコンソールに表示されない返り値を返す

foo <- function(x) {return(x)}
foo(1)

## [1] 1

foo <- function(x) {invisible(x)}
foo(1)            # 何も表示されない
x <- foo(1)
x                 # 結果は変数 x に付値されている

## [1] 1

注意：invisible() 関数は関数の返り値の指定に使われるだけでなく，次のような使い方もできる．

test <- function(x) {print(x); x <- x+1; x}
test(3)

## [1] 3

## [1] 4

# [1] 3      # print(x) による出力
# [1] 4      # 関数 test の返り値
temp <- invisible(test(3))

## [1] 3

temp

## [1] 4

●永続付値演算子で間接的に返り値を返す
関数中で永続付値演算子を使うと，関数終了後も残る値を変数に付値できる．関数実行前には存在しなかった変数を作ることもできる．永続付値演算子 \(\verb+<<-, ->>+\) は現在の実行環境の親環境(しばしば \(\verb+R+\) の大局的環境 ( \(\verb+.GlobalEnv?+\) という名前の隠しオブジェクト)中のオブジェクトに対する操作*1 であり，特に関数中で用いるときは 注意がいる．一方で，親環境のオブジェクトへの付値はその関数が終了後も残り，特に大局的環境中のオブジェクトは任意の関数から直ちに参照でき，特に副関数に複雑な引数を引き渡すとき便利である．永続付値演算子を関数中で用いるとき陥りやすい間違いは次の例でみられる:

v <- 1
test <- function () {v <- 2; v <<- 3; cat("v=", v, "\n")}
test()

## v= 2

v      # いつのまにか値が変わっている

## [1] 3

大局的変数への永続付値の便利な使い方は，他の関数で使うべき値を暗黙のうちに引き渡すことである(次の例を参照).

foo <- function (x, y, z) {.w <<- list(x, y, z)}    # 大局的変数 .w に付値
foo2 <- function () {.w[[1]] + .w[[2]] + .w[[3]]}   
                  #  大局的変数 .w を暗黙のうちに参照
foo(1, 2, 3)   #  これで大局的変数 .w (=list(1, 2, 3)) が作られる
foo2()

## [1] 6

●stop() 関数
stop() 関数は，現在の表現式の実行を中断し，その引数として与えられたメッセージを表示し，それから options(error=…) で指定された，エラー時動作を実行する．既定では トップレベルのプロンプトに戻る

# x が負またはゼロなら中断，正なら log(x) を返す関数
foo <- function(x) {
         ifelse( x<=0, stop(message="non-positive arg!"), log(x))
         }
foo(3)

## [1] 1.098612

#foo(-3)

●warning() 関数
警告メッセージを生成する． 実際の結果は options(“warn”) の値に依存する

* warn が負なら警告は無視される
* warn が零ならば一旦保存され，最上位の関数が終了した際に出力される
* warn が 1 ならば警告が生起するとすぐに出力され， 2 (もしくはそれ以上)ならば警告はエラーとして処理される

 foo <- function(x) {
            if (x<=0) {return(NA); warning(message="NA produced")}
            else return(log(x))
          }
 foo(3)

## [1] 1.098612

 foo(-3)   # エラーメッセージを表示し中断

## [1] NA

* 結果は options("warn") の値に依存する
* もし warn が負なら警告は無視される
* もしそれが零ならば一旦保存され 最上位の関数が終了した際に出力される
* もしそれが 1 ならば警告が生起するとすぐに出力される
* 2(もしくはそれ以上)ならば警告はエラーとして処理される．

●stopifnot()関数
引数としてカンマで区切って並べられた条件が満たされないときにプログラムをストップする． （stopif という関数仕様の方が素直で便利だと思うのだが）

 a <-3
 b <- 5
 stopifnot(a == 3, b==5)  # 条件 a==3 & b==5 が満たされないとき停止する

●匿名関数
名前の無い関数があり得る．例えば関数中である特別な値を一時的に作りたいときなどに使う

(function(z){dnorm(z)})((0:8)/2)  # N(0,1) の密度関数の値

## [1] 0.3989422804 0.3520653268 0.2419707245 0.1295175957
## [5] 0.0539909665 0.0175283005 0.0044318484 0.0008726827
## [9] 0.0001338302

foo <- function (x) {y <- (function(z){dnorm(z)})((0:8)/2); x*y}  
             # N(0, x^2) の密度関数
foo(2)

## [1] 0.7978845608 0.7041306535 0.4839414490 0.2590351913
## [5] 0.1079819330 0.0350566010 0.0088636968 0.0017453654
## [9] 0.0002676605

●関数の再帰的定義
関数の定義中に，その関数自身が登場しても良い．当然，登場した関数の値が合理的に定義可能である必要がある

foo <- function(x) {ifelse(x==1, 1, x*foo(x-1))}  # 即席階乗関数
foo(1)        # 1!

## [1] 1

foo(3)        # 3! (foo(3) を計算する際，foo(1) は既に定義済み)

## [1] 6

●関数内部での関数定義
R の関数内部には別の関数定義を置き，その場で実行できる．但し，内部関数は単独では存在しない

foo <- function() {
          foo2 <-  function() {   # 関数内部での関数定義  
             x <- 1:3; y <- 23:34; z <- cbind(x, y); 
             out <- list(x=x,y=y,z=z); return(out)
             } # end of foo2
          c <- foo2()           # その場で実行
          return(list(c$z, c$x, c$y)) 
          } # end of foo
x <- foo()
x[[3]]

##  [1] 23 24 25 26 27 28 29 30 31 32 33 34

foo2()                                # 関数 foo2 は foo 終了後は存在しない

## [1] 6

foo <- function (x) {
                 y <- x
                 temp <- function (a) a*y   
                       # temp 定義中の変数 y は直前の行で定義された変数
                 temp(2) }
foo(4)

## [1] 8

●二項演算子型の関数
R における +, -, *, / 等の組み込み二項演算子も特殊な形の関数である．R には 独自に二項演算子を定義する機構がある．

"%+=%" <- function(x, y) {x <<- x + y}  # C 風のインクリメント演算子
x <- 10
x %+=% 5
x          # x は 5 だけ増えている

## [1] 15

●関数を返す関数
R の関数は R の任意のオブジェクトを返すことができる．当然関数オブジェクトを 返すことも可能．次の例を参照．関数生成関数 foo への引数が，返り値関数の内部 パラメータになっていることを注意(つまり返り値である関数 Foo の附属環境に登録 されている)．

foo <- function(a, b)  {function (x, y) a*x + b*y}
Foo <- foo(2, 3)    # Foo(x,  y) は関数 2*x + 3*y
Foo

## function (x, y) a*x + b*y
## <environment: 0x55ae93576578>

Foo(1, 2)

## [1] 8

Foo                    # 定義を見る (a=1, b=2 の情報は附属環境に含まれており表に見えない)

## function (x, y) a*x + b*y
## <environment: 0x55ae93576578>

Foo <- foo(-2, -3)     # Foo(x, y) は関数 (-2)*x + (-3)*y
Foo(1, 2)

## [1] -8

●関数の後始末 on.exit()
on.exit(EXPR) は関数が正常・異常終了した際に EXPR を実行する．関数中で変更した R の基本的設定を元に戻すのに便利．on.exit(EXPR, add=TRUE)は先の on.exit 関数の 実行内容に付け加える．

foo <- function() {
       old.par <- par(no.readonly = TRUE) # 現在の作図パラメータ記録
       on.exit(par(oldpar))               # 関数終了時に元に戻す
       on.exit(dev.off(), add=TRUE)       # 更に，関数終了時にデバイスを閉じる
       png("foo.png")                     # png デバイスを開く
       # --- 幾つかの作図命令 ---
    } # end of foo

●関数の実行速度の計測 system.time()

system.time(for (i in 1:10000) mean(runif(500)))

##    user  system elapsed 
##   0.275   0.020   0.295

時間関数の返すベクトルは順に (最後の二つは普通ゼロ)

* ユーザーCPUタイム
* システムCPUタイム
* 経過時間
* 副プロセスの使用ユーザーCPUタイム
* 副プロセスの使用システムCPUタイム
* 時間の解像度はシステム固有であり，普通 1/100 秒．経過時間は最も近い時間に 1/100 秒単位で丸められる．

●速度の向上
Rは所詮インタプリター言語であり，コンパイラー型言語に比べれば速度が劣るのは致し方ない．それでも，R言語の特性をうまく使えば信じられないほどの速度を達成することも夢では無い．いくつかのヒントをあげる

● むき出しの論理判断はできるだけ避ける
論理判断は如何なる言語でも相対的に時間を食う．避けられないことも多いが，工夫で避けられることもある．R の組み込み関数はできるだけ速度が早くなるように工夫(しばしば C や Fortran サブルーティンを使用)されているので，それを使うことが好ましい.

foo <- function(x) {if(x<=0) return(-x) else return(x)}        # 手製の絶対値関数 
system.time(for (i in 1:100000) {x=runif(1)-0.5; foo(x)} )

##    user  system elapsed 
##   0.325   0.015   0.342

system.time(for (i in 1:100000) {x=runif(1)-0.5; abs(x)} )     # 餅は餅屋の例え

##    user  system elapsed 
##   0.208   0.000   0.208

system.time(for (i in 1:100000) {x=runif(1)-0.5; sqrt(x^2)} )  # これでも少しはまし

##    user  system elapsed 
##   0.203   0.000   0.204

system.time(for (i in 1:100000) {x=runif(1)-0.5; max(x,-x)} )

##    user  system elapsed 
##   0.233   0.000   0.233

foo <- function (x) {ifelse (x==0, 1, 0)}  # 引数 x は 0 か 1 とする
x <- floor(2*runif(100000))    # 長さ 10000 の 0, 1 ベクトル
system.time(foo(x))

##    user  system elapsed 
##   0.003   0.000   0.004

foo2 <- function (x) 1-x          # 実は foo と同値
system.time(foo2(x))

##    user  system elapsed 
##   0.000   0.000   0.001

● for ループはできるだけ避ける
R はベクトル・配列演算を内部 C ルーティンで処理し，高速になるように最適化されている．for ループはしばしばベクトル・配列演算で代用できる．しかもコードが短くなり，可読性が高まると言うおまけもつく

foo <- function (X, Y) {     # 二つの 100x100 行列の愚直な掛け算
                 Z <- matrix(0,ncol=100, nrow=100)
                 for (i in 1:100)
                 for (j in 1:100)
                 for (k in 1:100) Z[i,j] <- Z[i,j] + X[i,k]*Y[k,j]
              Z}
X <- matrix(runif(10000), ncol=100)  # 100x100 行列を定義
Y <- matrix(runif(10000), ncol=100)  # 同上
system.time(Z<-foo(X, Y))

##    user  system elapsed 
##   0.251   0.000   0.252

system.time(Z <- X%*%Y)  # 専用演算子を使用

##    user  system elapsed 
##       0       0       0

●コードのボトルネックの発見 Rprof()
関数の実行速度をあげるためには，どの部分で時間を喰っているか確認する必要がある．普通，関数の実行時間の大部分は極少数のコードの実行に当てられていることが多い．その部分を改良すれば，大幅な速度の向上が期待できる．Rprof() *3 はコード中の各実行単位の使用回数を，一定のサンプリング期間毎にチェックし，レポートファイル(既定では Rporf.out)を作成する．結果はレポートファイルを直接みても良いし，命令 summaryRprof() で簡潔に一覧することもできる．

Rprof()    
   # 既定のログファイル Rprof.out とサンプリング間隔 0.02秒 でプロファイル開始 
x <- y <- matrix(runif(10^6),ncol=1000)  # 大きな行列
z <- x%*%y   # その掛け算
Rprof(NULL)  # プロファイル終了
summaryRprof()  # 既定のログファイル Rprof.out からプロファイル結果要約

## $by.self
##              self.time self.pct total.time total.pct
## "%*%"             0.24    85.71       0.24     85.71
## "NextMethod"      0.02     7.14       0.02      7.14
## "runif"           0.02     7.14       0.02      7.14
## 
## $by.total
##                         total.time total.pct self.time
## "block_exec"                  0.28    100.00      0.00
## "call_block"                  0.28    100.00      0.00
## "evaluate_call"               0.28    100.00      0.00
## "evaluate::evaluate"          0.28    100.00      0.00
## "evaluate"                    0.28    100.00      0.00
## "in_dir"                      0.28    100.00      0.00
## "knitr::knit"                 0.28    100.00      0.00
## "process_file"                0.28    100.00      0.00
## "process_group.block"         0.28    100.00      0.00
## "process_group"               0.28    100.00      0.00
## "rmarkdown::render"           0.28    100.00      0.00
## "withCallingHandlers"         0.28    100.00      0.00
## "eval"                        0.26     92.86      0.00
## "handle"                      0.26     92.86      0.00
## "timing_fn"                   0.26     92.86      0.00
## "withVisible"                 0.26     92.86      0.00
## "%*%"                         0.24     85.71      0.24
## "NextMethod"                  0.02      7.14      0.02
## "runif"                       0.02      7.14      0.02
## ".make_numeric_version"       0.02      7.14      0.00
## "[.simple.list"               0.02      7.14      0.00
## "["                           0.02      7.14      0.00
## "getRversion"                 0.02      7.14      0.00
## "handle_output"               0.02      7.14      0.00
## "matrix"                      0.02      7.14      0.00
## "package_version"             0.02      7.14      0.00
## "paste"                       0.02      7.14      0.00
## "plot_snapshot"               0.02      7.14      0.00
## "R_system_version"            0.02      7.14      0.00
## "recordPlot"                  0.02      7.14      0.00
## "structure"                   0.02      7.14      0.00
## "w$get_new"                   0.02      7.14      0.00
##                         self.pct
## "block_exec"                0.00
## "call_block"                0.00
## "evaluate_call"             0.00
## "evaluate::evaluate"        0.00
## "evaluate"                  0.00
## "in_dir"                    0.00
## "knitr::knit"               0.00
## "process_file"              0.00
## "process_group.block"       0.00
## "process_group"             0.00
## "rmarkdown::render"         0.00
## "withCallingHandlers"       0.00
## "eval"                      0.00
## "handle"                    0.00
## "timing_fn"                 0.00
## "withVisible"               0.00
## "%*%"                      85.71
## "NextMethod"                7.14
## "runif"                     7.14
## ".make_numeric_version"     0.00
## "[.simple.list"             0.00
## "["                         0.00
## "getRversion"               0.00
## "handle_output"             0.00
## "matrix"                    0.00
## "package_version"           0.00
## "paste"                     0.00
## "plot_snapshot"             0.00
## "R_system_version"          0.00
## "recordPlot"                0.00
## "structure"                 0.00
## "w$get_new"                 0.00
## 
## $sample.interval
## [1] 0.02
## 
## $sampling.time
## [1] 0.28

参考
 $by.self
             self.time self.pct total.time total.pct
 "%*%"           2.26  71.5  2.26  71.5      # 行列掛け算がやはり一番時間を喰う
 "runif"            0.42  13.3  0.42  13.3   # 一様乱数生成がその次
 "as.vector"    0.24   7.6   0.66   20.9  
                          # (恐らく) ベクトルを行列化するオーバーヘッド
 "matrix"         0.24   7.6   0.90   28.5  
                          # (恐らく) ベクトルを行列化するオーバーヘッド
 
 $by.total
             total.time total.pct self.time self.pct
 "%*%"            2.26      71.5      2.26     71.5
 "matrix"          0.90      28.5      0.24      7.6
 "as.vector"     0.66      20.9      0.24      7.6
 "runif"            0.42      13.3      0.42     13.3
 
 $sampling.time
 [1] 3.16

●使い勝手の向上
使い勝手の向上はしばしば速度と反比例するが，より好ましいことが多い

● 関数のベクトル化
R の多くの組み込み関数は意味がある限りできるだけベクトル化されている．引数にベクトルを与えることができ，対応する返り値もベクトルになる．こうすることにより，むき出しの for ループを隠し，コードの短縮化ができ，可読性も高まる．

x <- 1:10   # 等差数列
x^2         # 巾乗関数もベクトル化されている

##  [1]   1   4   9  16  25  36  49  64  81 100

x <- matrix(1:16, ncol=4)
x^2                           # それどころか行列化されている!(行列はベクトルの拡張)

##      [,1] [,2] [,3] [,4]
## [1,]    1   25   81  169
## [2,]    4   36  100  196
## [3,]    9   49  121  225
## [4,]   16   64  144  256

choose(10, 0:10)       # 二項係数もベクトル化されている!

##  [1]   1  10  45 120 210 252 210 120  45  10   1

choose(10:13, 10)

## [1]   1  11  66 286

choose(10:13, 0:10)   # はてこれは何を計算してくれたのだろう?

##  [1]    1   11   66  286  210  462  924 1716   45   55   66

runif(10)>0.5              # 論理判断もベクトル化されている!

##  [1] FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
## [10]  TRUE

# ベクトル化された表現式だけを使えば結果は自然にベクトル化される

foo <- function (x) sin(x>0.5) # 関数 foo の定義 
              # R では論理値 TRUE, FALSE は数値 1, 0 とも解釈される
foo(runif(10))

##  [1] 0.000000 0.000000 0.841471 0.000000 0.000000 0.841471
##  [7] 0.841471 0.841471 0.000000 0.000000

# 無理矢理ベクトル化する方法の例
 
foo <- function(x) if (x<0) return(2) else return(3)  
                         # ベクトル化されていない関数の例
foo(runif(10) - 0.5)  # x の最初の要素だけ受け付ける 

## Warning in if (x < 0) return(2) else return(3): 条件が長さが
## 2 以上なので、最初の 1 つだけが使われます

## [1] 3

foo <- function (x) {  # そのベクトル化版
                 temp <- function(x) if (x<0) return(2) else return(3)
                 sapply(x, temp) }  
         # sapply 関数は x の各要素に temp を施した結果のベクトルを返す関数
foo(runif(10)-0.5)

##  [1] 2 2 2 3 2 2 3 3 3 3

# ベストアンサー 
ifelse(runif(10) - 0.5 < 0, 2, 3)  # 実はベクトル化された関数 ifelse を使えばすんだこと

##  [1] 3 2 2 3 3 3 3 2 3 3

●missing() 関数(仮)引数が存在するかどうかチェック
R 関数の仮引数の数は場合により変わり得るので，ある引数が実際に存在するかどうかチェックする必要が起こる

  myplot <- function(x, y) {
                    if(missing(y)) {
                        y <- x  
                           # もし仮引数 y が与えられなければ y <- x とする 
                        x <- 1:length(y)
                    }
                    plot(x,y)
                  }
x <- (0:10)^2
myplot(x)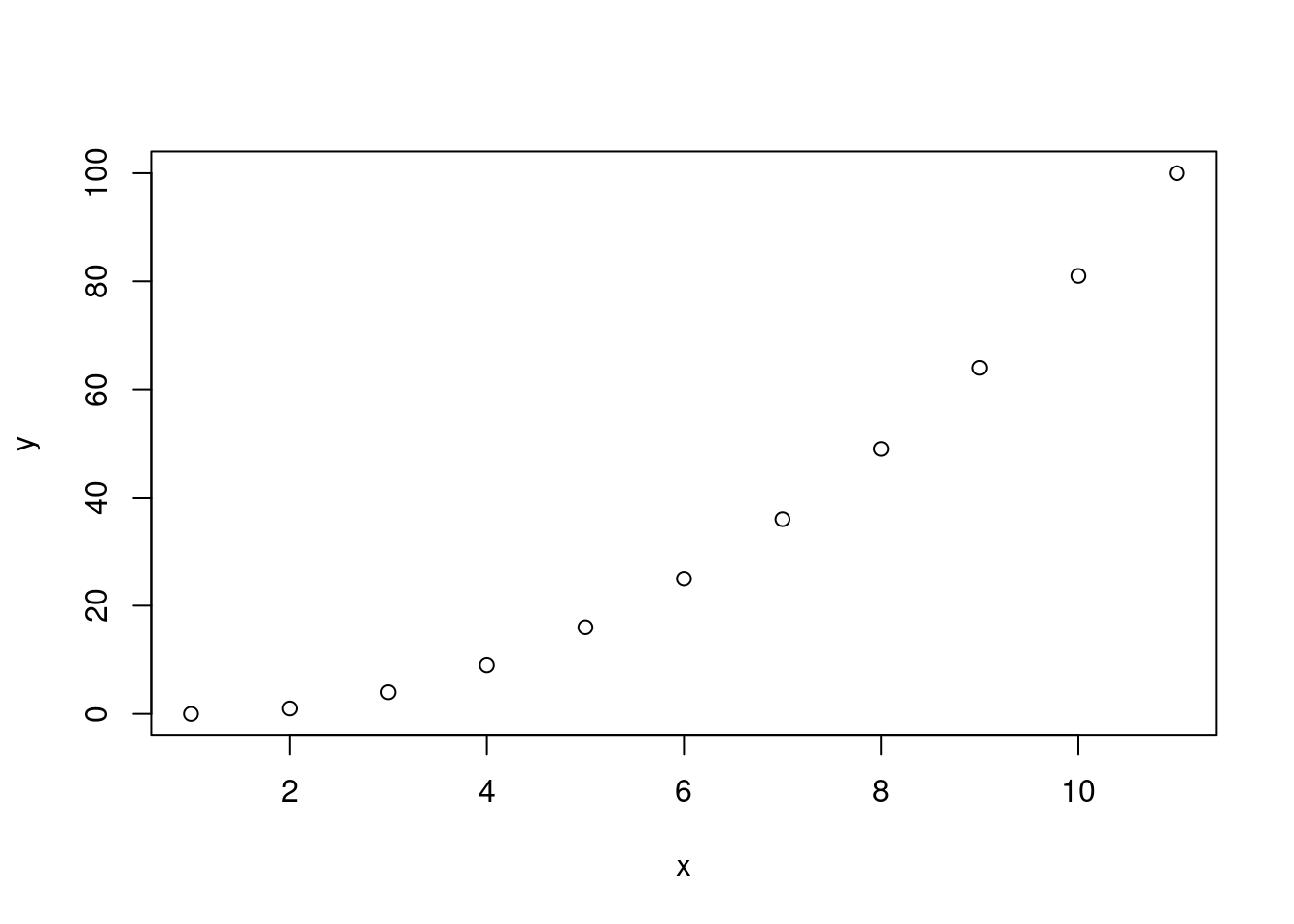

●関数引数のマッチング match.arg
関数の引数に与えられた値が候補のどれに一致するかどうかチェックする

書式 (choice 引数は候補リストのベクトル) match.arg(arg, choices) 部分的マッチングが行なわれるが，返り値は非省略形で与えられる． 該当する項目がなければエラーメッセージがでる

center <- function(x, type = c("mean", "median", "trimmed")) {
  type <- match.arg(type)
  switch(type,                     # match.type の結果により switch
              mean = mean(x),
              median = median(x),
              trimmed = mean(x, trim = .1))
  } # end of center
x <- rcauchy(10)
center(x, "t")         # 部分的マッチングで type="trimmed" とされた

## [1] -0.05519232

center(x, "med")   # 部分的マッチングで type="median" とされた

## [1] 0.04875689

# center(x, "m")       # エラー(m で始まる候補が二つある)

●関数の形式引数を得る，設定する

f <- function(x) a+b  # 関数の定義
formals(f)  # 関数 f の形式的引数は？

## $x

formals(f) <- alist(a=, b=3)  # 形式的引数 x を a ,b (b は既定値 3 付き)
f                # f の定義を確認

## function (a, b = 3) 
## a + b

f(2)

## [1] 5

f(2, 5)

## [1] 7

f <- function() x
formals(f) <- alist(x = , y = 2, ... = )  # 「その他大勢」引数 ... の設定
f

## function (x, y = 2, ...) 
## x

●関数本体を表示，設定する body()

foo <- function() x  # 関数を定義
body(foo)            # 関数本体を表示

## x

body(foo) <- expression(x^2) # 関数本体を再定義
foo                          # 確かに変わっている

## function () 
## x^2

  fd <- deriv(~ 100*(x2 - x1*x1)^2 + (1-x1)^2, c("x1", "x2")) 
                              #  関数の数式一階偏微分
  fdd <- function(x1, x2) {}  # 空の関数定義
  body(fdd) <- fd             # 関数の本体を fd とする

●オブジェクト生成

# 文字ベクトルや数値を用いてあるオブジェクト名をプログラム中で生成し，付値するには
assign(paste("file", 1, "max", sep=""), 1)
ls()

##  [1] "%+=%"       "a"          "A"          "AT"        
##  [5] "b"          "center"     "D"          "dens"      
##  [9] "df"         "digitsBase" "exp"        "exp1"      
## [13] "f"          "fd"         "fdd"        "file"      
## [17] "file1max"   "fname"      "foo"        "Foo"       
## [21] "foo1"       "foo2"       "func1"      "i"         
## [25] "ind"        "line"       "lst"        "Lst"       
## [29] "M"          "M1"         "M2"         "myplot"    
## [33] "out"        "ox"         "res"        "s"         
## [37] "str"        "sw1"        "sw2"        "temp"      
## [41] "test"       "v"          "v1"         "vec"       
## [45] "w"          "w0"         "w1"         "w2"        
## [49] "x"          "X"          "y"          "Y"         
## [53] "z"          "Z"

# 変数 var1,var2,...,var10 を生成し，それぞれ値 1,2,...,10 を代入
for (i in 1:10) assign(paste("var", i, sep=""), i)
# file[1],...,file[10] はデータファイル名の文字列であるとして，次の関数は
# それを読み込み，順に f1,f2,...,f10 という名前のオブジェトに付値

 temp <- function() {
   for (i in 1:10) {
     assign(paste("f",i,sep=""), read.table(file[i],skip=1))
   } # end of for-i
 } # end of temp

# 順に通し番号付きの名前 d1, d2, d3 の変数を作り，それに値 x1-x2, y1-y2,z1-z2 の値を代入 

 x1 <- rnorm(10); x2 <- rnorm(10)
 y1 <- rnorm(10); y2 <- rnorm(10)
 z1 <- rnorm(10); z2 <- rnorm(10)
 names. <- c("x", "y", "z") # 文字ベクトル
 for(i in names.){
    # (順に)変数 x1, y1, z1 の値を res1 に代入
    res1 <- get(paste(i,"1",sep=""))
    # (順に)変数 x2, y2, z2 の値を res2 に代入
    res2 <- get(paste(i,"2",sep=""))
    # (順に)変数 d1, d2, d3 を作り，それに値 res1-res2 を代入
    assign(paste("d",i,sep=""), res1-res2)
 } 
ls()

##  [1] "%+=%"       "a"          "A"          "AT"        
##  [5] "b"          "center"     "D"          "dens"      
##  [9] "df"         "digitsBase" "dx"         "dy"        
## [13] "dz"         "exp"        "exp1"       "f"         
## [17] "fd"         "fdd"        "file"       "file1max"  
## [21] "fname"      "foo"        "Foo"        "foo1"      
## [25] "foo2"       "func1"      "i"          "ind"       
## [29] "line"       "lst"        "Lst"        "M"         
## [33] "M1"         "M2"         "myplot"     "names."    
## [37] "out"        "ox"         "res"        "res1"      
## [41] "res2"       "s"          "str"        "sw1"       
## [45] "sw2"        "temp"       "test"       "v"         
## [49] "v1"         "var1"       "var10"      "var2"      
## [53] "var3"       "var4"       "var5"       "var6"      
## [57] "var7"       "var8"       "var9"       "vec"       
## [61] "w"          "w0"         "w1"         "w2"        
## [65] "x"          "X"          "x1"         "x2"        
## [69] "y"          "Y"          "y1"         "y2"        
## [73] "z"          "Z"          "z1"         "z2"

●文字列を評価実行 : eval(parse(text=…)

eval(parse(text="ls()"))

##  [1] "%+=%"       "a"          "A"          "AT"        
##  [5] "b"          "center"     "D"          "dens"      
##  [9] "df"         "digitsBase" "dx"         "dy"        
## [13] "dz"         "exp"        "exp1"       "f"         
## [17] "fd"         "fdd"        "file"       "file1max"  
## [21] "fname"      "foo"        "Foo"        "foo1"      
## [25] "foo2"       "func1"      "i"          "ind"       
## [29] "line"       "lst"        "Lst"        "M"         
## [33] "M1"         "M2"         "myplot"     "names."    
## [37] "out"        "ox"         "res"        "res1"      
## [41] "res2"       "s"          "str"        "sw1"       
## [45] "sw2"        "temp"       "test"       "v"         
## [49] "v1"         "var1"       "var10"      "var2"      
## [53] "var3"       "var4"       "var5"       "var6"      
## [57] "var7"       "var8"       "var9"       "vec"       
## [61] "w"          "w0"         "w1"         "w2"        
## [65] "x"          "X"          "x1"         "x2"        
## [69] "y"          "Y"          "y1"         "y2"        
## [73] "z"          "Z"          "z1"         "z2"

eval(parse(text = "x[3] <- 5"))
x[3]

## [1] 5

hoge <- function(a, b) {
     w <- paste("temp <- function(x) {",sep="")
     w <- paste(w, a, "*x + ", b, "}     ",sep="")
     cat("w =",w,"\n")
     eval(parse(text=w))
     temp(9) }

hoge(1,2)  # 内部で関数 temp(x) が定義され，temp(9) を計算する

## w = temp <- function(x) {1*x + 2}

## [1] 11

●文字列を与えて，それを名前に持つオブジェクトの値を得る, get() 関数

xyz <- 1:5
get("xyz")

## [1] 1 2 3 4 5

eval(parse(text="xyz")) # これでも良い

## [1] 1 2 3 4 5

foo <- function(x) x^2
get("foo")

## function(x) x^2

eval(parse(text="foo")) # これでも良い

## function(x) x^2

●関数から複数の値を返す (リスト返り値)
一つの関数から複数の値を返すにはそれらをリストにまとめて返す.

# 名前タグを自前で指定するには明示的に名前付きリストを返り値にする
test <- function(x){y=log(x);z=sin(x);return(list(value=x,log=y,sin=z))}
test(1:3)

## $value
## [1] 1 2 3
## 
## $log
## [1] 0.0000000 0.6931472 1.0986123
## 
## $sin
## [1] 0.8414710 0.9092974 0.1411200

●エラー続行 シミュレーション等でエラーが起こる可能性のある場合，続けて次のシミュレーションを続行するのに便利．

 #書式
 try(expr, silent = FALSE, first = TRUE)
 # expr は実行可能な表現
 # silent =TRUE ならエラーコードを表示しない

     ## シミュレーションを100回実行，エラーにならなかった場合の結果を記録
     set.seed(123)  # 結果を再現できるように乱数種を指定
     x <- rnorm(50) # 正規乱数50個
     doit <- function(x)  # シミュレーションコード
     {
         x <- sample(x, replace=TRUE)  
                             # x から重複を許して(x と同じ数だけ)無作為抽出
         if(length(unique(x)) > 30) mean(x) 
                             # 重複を除いて 31 個以上なら平均計算
         else stop("too few unique points") # さもなければ中断
     }
     ## doit を10回実行し，結果をリスト res に連続記録
     res <- lapply(1:10, function(i) try(doit(x), TRUE))
     res

## [[1]]
## [1] "Error in doit(x) : too few unique points\n"
## attr(,"class")
## [1] "try-error"
## attr(,"condition")
## <simpleError in doit(x): too few unique points>
## 
## [[2]]
## [1] 0.1038463
## 
## [[3]]
## [1] "Error in doit(x) : too few unique points\n"
## attr(,"class")
## [1] "try-error"
## attr(,"condition")
## <simpleError in doit(x): too few unique points>
## 
## [[4]]
## [1] "Error in doit(x) : too few unique points\n"
## attr(,"class")
## [1] "try-error"
## attr(,"condition")
## <simpleError in doit(x): too few unique points>
## 
## [[5]]
## [1] 0.2203698
## 
## [[6]]
## [1] -0.05966616
## 
## [[7]]
## [1] 0.370867
## 
## [[8]]
## [1] 0.06650469
## 
## [[9]]
## [1] 0.07928817
## 
## [[10]]
## [1] 0.06637614

●丸括弧の不思議 (付値と表示を同時に行なう)

x=1:4    # 付値のみで結果の表示はない
(x=1:4)  # 丸括弧で囲むと，付値した結果を表示

## [1] 1 2 3 4

test1 <- function(x) { y <- 2*x }
test1(1:4)  # 何も表示されない
test2 <- function(x) { (y <- 2*x) }
test2(1:4) # 丸括弧で囲むと付値した上で表示される

## [1] 2 4 6 8

●論理値の数値化
R の論理値 TRUE, FALSE は数値が必要とされる文脈では整数値 1, 0 に強制変換 されるが，明示的に数値に変換するには次のようにする．

x <- matrix(1:4, 2, 2)
x

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

xx <- x>2.5
xx                  # 論理値行列

##       [,1] [,2]
## [1,] FALSE TRUE
## [2,] FALSE TRUE

xx+0                # 数値に強制変換

##      [,1] [,2]
## [1,]    0    1
## [2,]    0    1

xx + 0:0            # 保管モードを整数にする(大規模行列ではメモリ使用量が減るメリット)

##      [,1] [,2]
## [1,]    0    1
## [2,]    0    1

 ## storage.mode(xx) <- "integer" でも良い
 ## as.integer 関数では行列属性を除いてしまう
as.integer(xx)  

## [1] 0 0 1 1

R では論理値 TRUE, FALSE は文脈に応じて整数 1,0 に強制変換されるので，表示の 際気持ちが悪いということがなければ，整数として使いたい場合でも特に整数に 明示的に変換する必要はない．それでも変換したければ次のようなトリックが使える．

is.integer(TRUE+FALSE) # 足し算をすれば強制変換される

## [1] TRUE

is.integer(TRUE*TRUE)  # かけ算をすれば強制変換される

## [1] TRUE

is.integer(TRUE+0:0)   # 0:0 は整数 0 になるからそれを足せば整数に強制変換される

## [1] TRUE

is.integer(TRUE*1:1)   # 1:1 は整数 1 になるからそれをかけると整数に強制変換される

## [1] TRUE

#is.real(x+0)           # 0 は実数とみなされるので結果も実数に強制変換される
as.integer(c(TRUE, FALSE))  # 明示的な整数への変換例

## [1] 1 0

(x <- matrix(c(TRUE, FALSE, FALSE, TRUE), c(2,2)))  # 論理値行列

##       [,1]  [,2]
## [1,]  TRUE FALSE
## [2,] FALSE  TRUE

x+0:0            # 整数値行列に変換

##      [,1] [,2]
## [1,]    1    0
## [2,]    0    1

●ダブルコロン演算子

    * 書式 pkg::name
    * 引数
          o pkg パッケージ名
          o name 変数・関数名(必要に応じ二重引用府で囲む)
    * 説明 パッケージ pkg 中の変数 name の値を返す．もしパッケージを未ロードならばロードされる．パッケージの名前空間への代入はできない．
    * 例

base::log # base パッケージ中の関数 log の情報を得る

## function (x, base = exp(1))  .Primitive("log")

function (x, base = exp(1))
 if (missing(base)) .Internal(log(x)) else .Internal(log(x, base))

## function (x, base = exp(1))
##  if (missing(base)) .Internal(log(x)) else .Internal(log(x, base))

base::"+" # base パッケージ中の関数 "+" の情報を得る

## function (e1, e2)  .Primitive("+")

もしパッケージもしくは自己定義関数中で既存の関数と同じ名前のオブジェクトを 重複定義しても，ダブルコロン演算子を使えば問題ない． インストール済みのパッケージをオンデマンドでロードするにも便利．

base::log(10)   

## [1] 2.302585

log <- function(x) exp(x) # log 関数の再定義
log

## function(x) exp(x)

log(1)                # 再定義による値

## [1] 2.718282

base::log(1) # 本来の log 関数の値が得られる

## [1] 0

●cut 関数 ： 数値ベクトルを指定した区間に分類する
値の分類区間を breaks ベクトルで与え，分類ラベルを labels で与える．ラベルは因子になるので，数値としてのあつかいはそのままでは不可能

x <- 2000*runif(10)
y <- cut(x, breaks=c(-Inf, 500, 1000, 2000, Inf), labels=c(0,1,2,3))
y

##  [1] 2 0 2 2 1 0 0 0 2 1
## Levels: 0 1 2 3

as.integer(y)  # 数値に変更

##  [1] 3 1 3 3 2 1 1 1 3 2

# ラベルを FALSE にすると区間のかずに応じたラベルが数値として与えられる 
y <- cut(x, breaks=c(-Inf, 500, 1000, 2000, Inf), labels=FALSE)
y # 結果は数値 0.1.2.3

##  [1] 3 1 3 3 2 1 1 1 3 2

# labels 引数を省略すると該当区間を表す文字列がラベル（因子）として与えられる
y <- cut(x, breaks=c(-Inf, 500, 1000, 2000, Inf))
y

##  [1] (1e+03,2e+03] (-Inf,500]    (1e+03,2e+03] (1e+03,2e+03]
##  [5] (500,1e+03]   (-Inf,500]    (-Inf,500]    (-Inf,500]   
##  [9] (1e+03,2e+03] (500,1e+03]  
## 4 Levels: (-Inf,500] (500,1e+03] ... (2e+03, Inf]

●指定秒数プログラムを休止する Sys.sleep

p1 <- proc.time()  # 現在の内部タイマーを得る
Sys.sleep(3.7)     # 3.7 秒実行休止  
proc.time() - p1   # 経過時間を得る

##    user  system elapsed 
##   0.005   0.000   3.705

● 再帰呼び出し
以下のような入れ子になったリストを考えてみる．

list(10, list(list(30, 20), 1:10), list(2:5))

ここで，このようなリストの末端にある数値を全て足す関数を定義してみる．このリストの個々の要素は同じ構造の（ただし入れ子が一段少ない）リストなので，個々の要素を自分自身を呼び出すことによって（再帰呼び出しによって）処理することが出来る．

# リスト x の末端にある数値の総和を求める関数
 myfunc <- function(x) {
   if (is.atomic(x)) return(sum(x)) # リストでなければ単に和を返す
   s <- 0                           # 変数を初期化
   for (i in x) {                   # リストの要素それぞれについて
     s <- s + myfunc(i)             # 末端の数値の和を計算してそれを加算していく
   }
   return(s)                        # 総和を返す
 }

 x <- list(10, list(list(30, 20), 1:10), list(2:5))
 x

## [[1]]
## [1] 10
## 
## [[2]]
## [[2]][[1]]
## [[2]][[1]][[1]]
## [1] 30
## 
## [[2]][[1]][[2]]
## [1] 20
## 
## 
## [[2]][[2]]
##  [1]  1  2  3  4  5  6  7  8  9 10
## 
## 
## [[3]]
## [[3]][[1]]
## [1] 2 3 4 5

 myfunc(x)

## [1] 129

# 次は再帰プログラムの例ではありきたりの階乗を求めるプログラムである．

 myfunc <- function(n) {
   if (n <= 1) return(1)
   else n * myfunc(n-1)
 }
 
 myfunc(5)

## [1] 120

# 改良版：ベクトルの各要素ごとに階乗を求められる
 myfunc2 <- function(x) {
   recurse <- (x>1)
   x[!recurse] <- 1
   if (any(recurse)) {
     y <- x[recurse]
     x[recurse] <- y*myfunc2(y-1)
   }
   return(x)
 }
 
 myfunc2(5)

## [1] 120

 myfunc2(1:10)

##  [1]       1       2       6      24     120     720    5040
##  [8]   40320  362880 3628800

● 数値積分
再帰関数を用いることで，数値積分を行うことが出来る．以下は数値積分を行う関数 area(関数, 左端の点, 右端の点) である．

 area <- function(f, a, b, eps = 1.0e-06, lim = 10) {
   fun1 <- function(f, a, b, fa, fb, a0, eps, lim, fun) {
     ## 関数‘fun1’ は‘area’ の中からだけ見える
     d <- (a + b)/2
     h <- (b - a)/4
     fd <- f(d)
     a1 <- h * (fa + fd)
     a2 <- h * (fd + fb)
     if(abs(a0 - a1 - a2) < eps || lim == 0)
       return(a1 + a2)
     else {
       return(fun(f, a, d, fa, fd, a1, eps, lim - 1, fun) +
              fun(f, d, b, fd, fb, a2, eps, lim - 1, fun))
     }
   }
   fa <- f(a)
   fb <- f(b)
   a0 <- ((fa + fb) * (b - a))/2
   fun1(f, a, b, fa, fb, a0, eps, lim, fun1)
 }
# 上の関数 area() を定義すると，以下のように積分計算が出来る．

 area(sin,0,pi/2) 

## [1] 0.999987

● R のオブジェクトに簡単なメモ代わりのコメントをつける comment()

comment 関数は任意オブジェクトにメモ代わりのコメントをつける．このコメントは print 関数では表示されない．詳しくは ?comment を参照．

 x <- matrix(1:12, 3, 4)
 # x にコメント属性として二つの文字列を加える
 comment(x) <- 
     c("This is my very important data from experiment #0234", "Jun 5, 1998")
 x  # コメントは表示されない！

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

 comment(x)  # コメントを表示する

## [1] "This is my very important data from experiment #0234"
## [2] "Jun 5, 1998"

 print(x)  # print 関数では表示されない！

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

 str(x)  # str 関数では表示される

##  int [1:3, 1:4] 1 2 3 4 5 6 7 8 9 10 ...
##  - attr(*, "comment")= chr [1:2] "This is my very important data from experiment #0234" "Jun 5, 1998"

 comment(x) <- c(comment(x), "revised Jun 7, 1998") # コメントを加える
 comment(x)

## [1] "This is my very important data from experiment #0234"
## [2] "Jun 5, 1998"                                         
## [3] "revised Jun 7, 1998"

 ## 日本語化 R でなくても日本語コメントなら大丈夫！
 ## オブジェクトを save, load しても大丈夫(らしい)
 comment(x) <- c("プロジェクト X データ","2003年11月12日")
 comment(x)

## [1] "プロジェクト X データ" "2003年11月12日"

 str(x)

##  int [1:3, 1:4] 1 2 3 4 5 6 7 8 9 10 ...
##  - attr(*, "comment")= chr [1:2] "プロジェクト X データ" "2003年11月12日"

 test <- function (x) x^2
 # 関数オブジェクトにもコメントを付けられる！
 comment(test) <- c("This is a test function.", "No meaning at all")
 comment(test)

## [1] "This is a test function." "No meaning at all"

 test                                 # コメントは表示されない！

## function (x) x^2

 comment(test) <- NULL  # コメントを消す
 comment(test)

## NULL

  Top   PageTop   PageEnd

6 グラフィックス

  Top   PageTop   PageEnd

r-g.html 参照

7 R言語に基づくデータ解析例

7.1 多変量データの基礎解析

options(width=60); source("/home/inoue/r-ex/RLIB")
# CSVファイルから読み込み
X0 <- read.csv("/home/inoue/r-ex/dex2.csv",header=T) 
head(X0,3); tail(X0,3)　　# 内容確認

##   No. 英語 数学 国語 社会
## 1   1   50   62   54   52
## 2   2   36   30   56   53
## 3   3   48   44   59   74

##    No. 英語 数学 国語 社会
## 38  38   47   65   67   65
## 39  39   45   48   63   75
## 40  40   35   35   62   75

df <- data.frame(X0[,-1]) # 第1カラムを除いてデータフレーム化
str(df)                   # データフレームdfの属性表示

## 'data.frame':    40 obs. of  4 variables:
##  $ 英語: int  50 36 48 50 40 46 45 76 62 43 ...
##  $ 数学: int  62 30 44 28 43 40 28 78 68 48 ...
##  $ 国語: int  54 56 59 53 66 51 75 70 58 69 ...
##  $ 社会: int  52 53 74 63 77 65 74 89 57 75 ...

head(df,3); tail(df,3)    # 最初の３例，最後の３例を表示

##   英語 数学 国語 社会
## 1   50   62   54   52
## 2   36   30   56   53
## 3   48   44   59   74

##    英語 数学 国語 社会
## 38   47   65   67   65
## 39   45   48   63   75
## 40   35   35   62   75

apply(df,2,mean)          # 変量毎の平均を求める

##   英語   数学   国語   社会 
## 49.725 49.550 60.950 65.575

var(df)                   # 分散・共分散行列を求める

##            英語        数学       国語       社会
## 英語  99.332692 106.8217949 20.0884615   2.905769
## 数学 106.821795 223.8948718  0.2589744 -31.862821
## 国語  20.088462   0.2589744 98.6641026  58.029487
## 社会   2.905769 -31.8628205 58.0294872 101.173718

apply(df,2,sd)            # 変量毎の標準偏差を求める

##      英語      数学      国語      社会 
##  9.966579 14.963117  9.932981 10.058515

cor(df)                   # 相関行列を求める

##            英語         数学        国語        社会
## 英語 1.00000000  0.716294628 0.202918195  0.02898552
## 数学 0.71629463  1.000000000 0.001742429 -0.21170362
## 国語 0.20291819  0.001742429 1.000000000  0.58081161
## 社会 0.02898552 -0.211703622 0.580811615  1.00000000

par(family="Japan1")
par(mfrow=c(2,2),cex=0.6)                  # 2x2の作図領域を確保
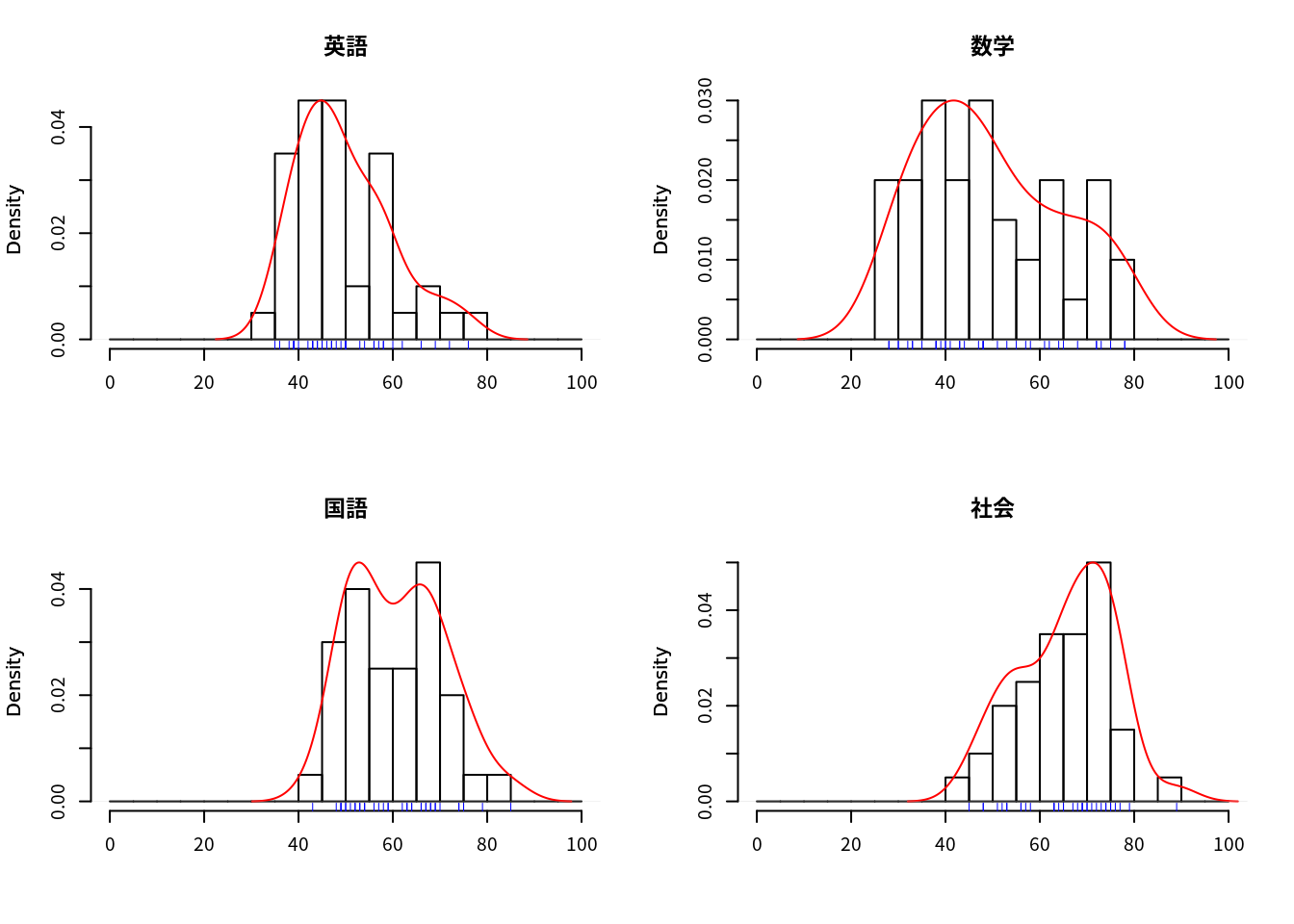
colnames(df)

## [1] "英語" "数学" "国語" "社会"

for (j in 1:ncol(df)) {                    # 変量毎のヒストグラム
  hist(df[,j],xlim=c(0,100),freq=F,breaks=seq(0,100,5),
       main=colnames(df[j]),xlab="") 
  par(new=T);                              # 推定密度関数の重ね書き
  plot(density(df[,j]),xlim=c(0,100),col="red",main="",xlab="",axes=F)
  rug(df[,j],col="blue")                   # データ点の描画を追記
  }

par(family="Japan1",pty="s",omd=c(0,1,0,1)); 
pairs(scale(df),xlim=c(-3.1,3.1),ylim=c(-3.1,3.1),cex=0.3)  # 対散布図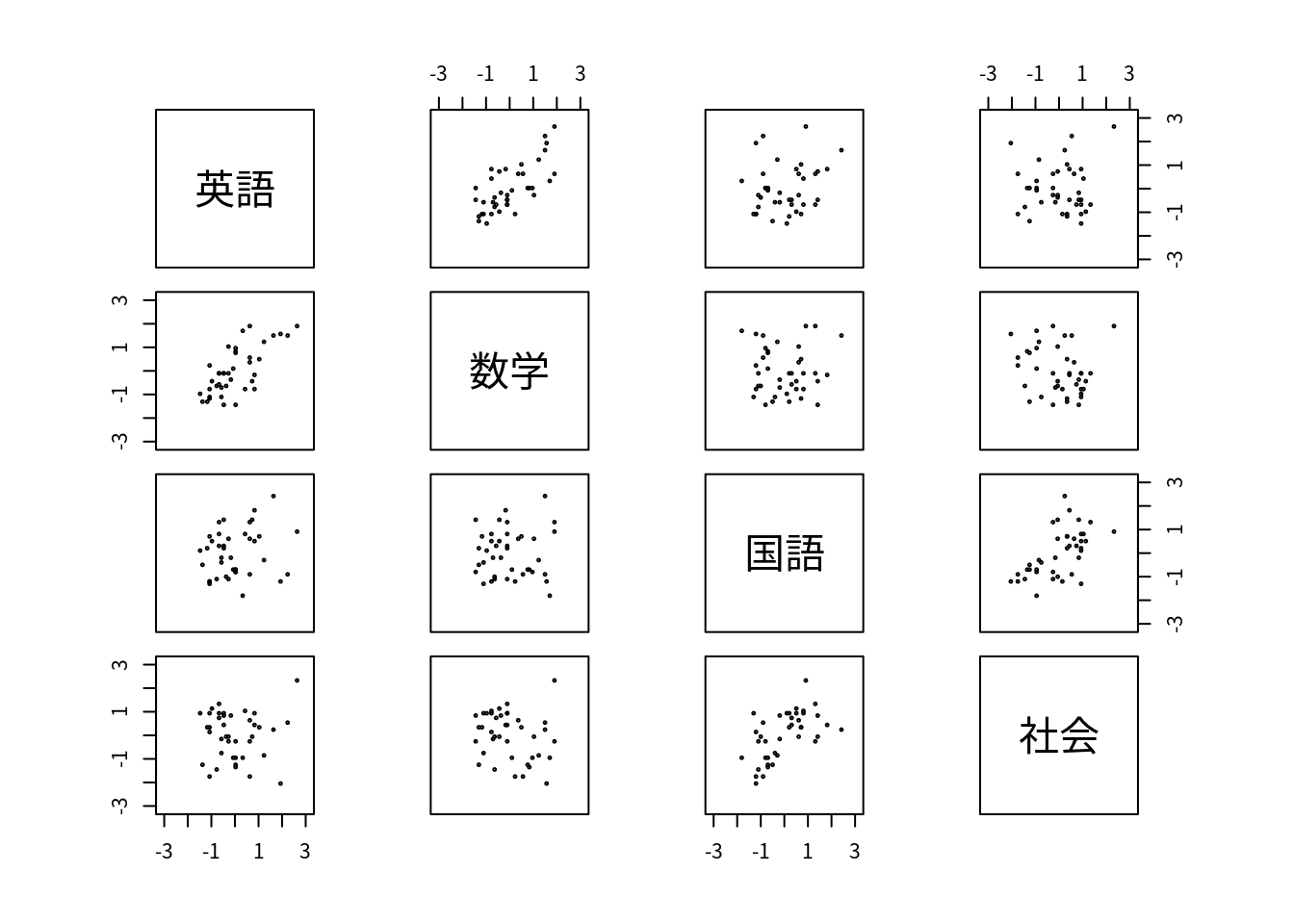 

par(family="Japan1"); pairs1(df)           # 私用ライブラリの利用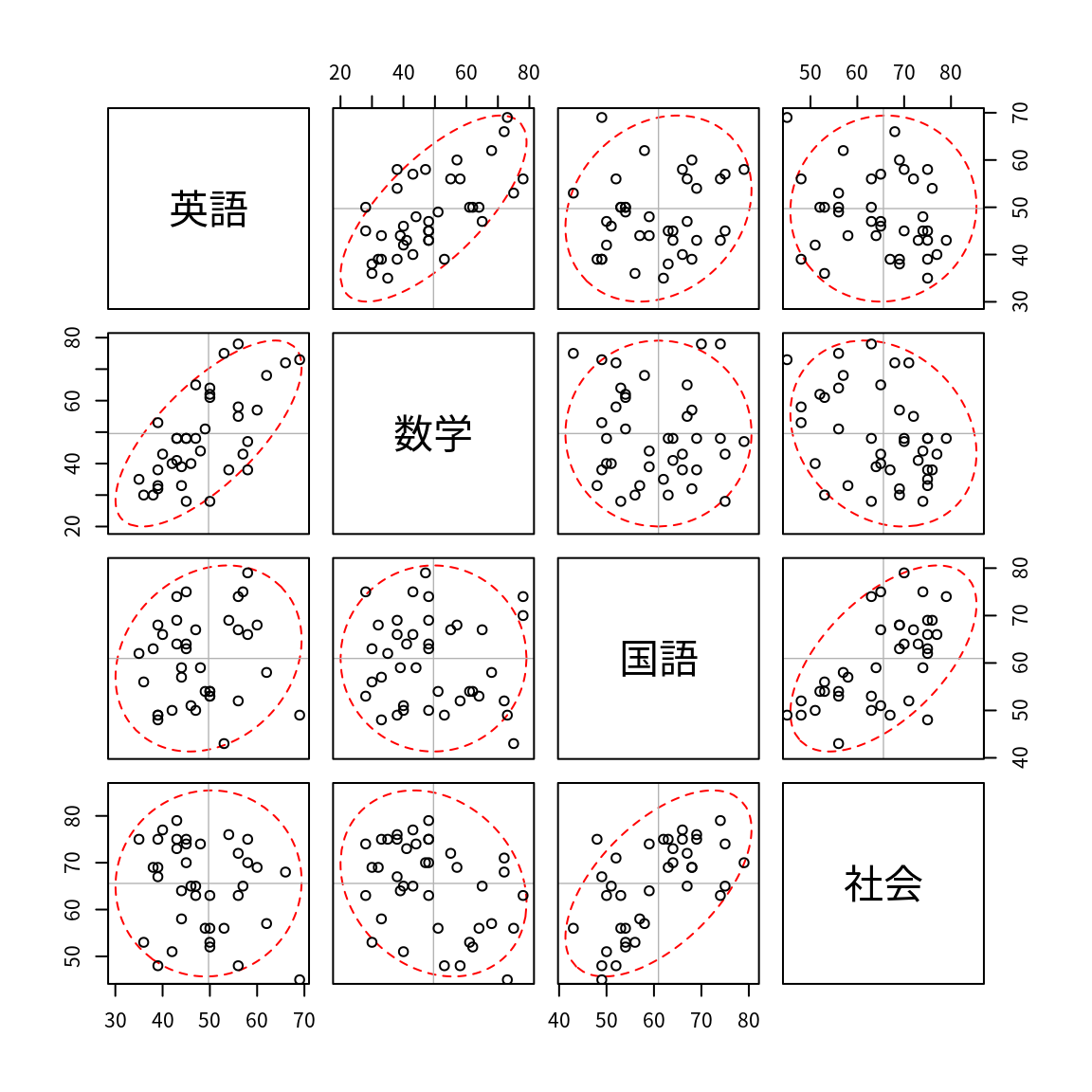

par(family="Japan1"); 
boxplot(df,main="箱ひげ図(四分位数）")      # 箱ひげ図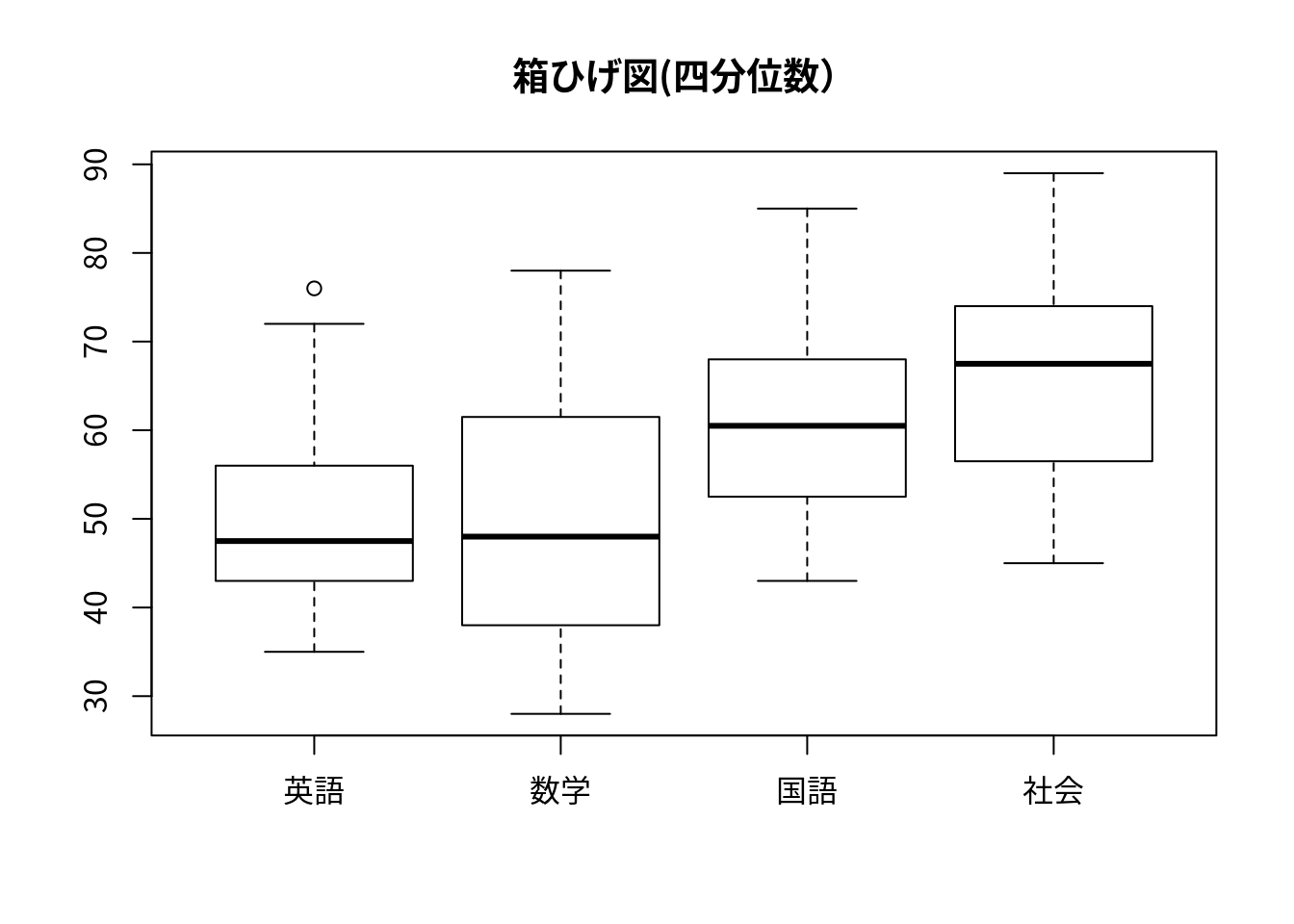

7.2 主成分分析，クラスタ分析，因子分析

prc <- prcomp(scale(df))                  # 主成分分析
summary(prc)

## Importance of components:
##                           PC1    PC2     PC3     PC4
## Standard deviation     1.3211 1.2715 0.62717 0.49459
## Proportion of Variance 0.4364 0.4042 0.09834 0.06115
## Cumulative Proportion  0.4364 0.8405 0.93885 1.00000

par(family="Japan1"); 
hc <- hclust(dist(scale(df)))
plot(hc,xlab="")                # クラスタ分析(デンドログラム)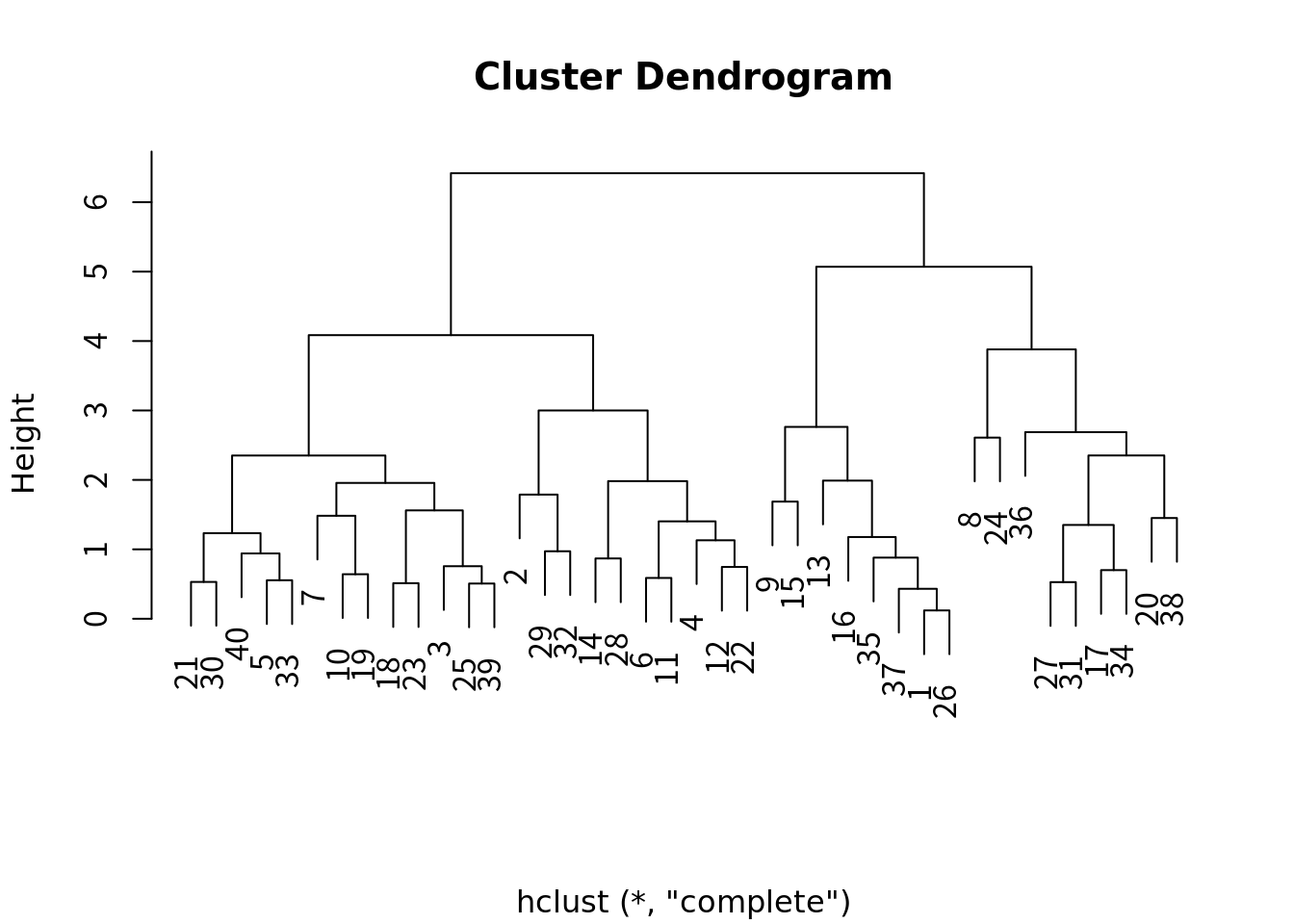

df[c(21,22,9,38),]

##    英語 数学 国語 社会
## 21   39   32   68   69
## 22   44   39   59   64
## 9    62   68   58   57
## 38   47   65   67   65

scale(df)[c(21,22,9,38),]

##            英語      数学       国語       社会
## [1,] -1.0760964 -1.172884  0.7097568  0.3405075
## [2,] -0.5744198 -0.705067 -0.1963157 -0.1565838
## [3,]  1.2316162  1.233032 -0.2969904 -0.8525116
## [4,] -0.2734138  1.032539  0.6090820 -0.0571655

pca1 <- pca(scale(df))                   # 主成分分析(因子分析)
#summary(pca1)
### 私用関数 pca.fig を定義する
pca.fig <- function(pca, label=c("x1","x2","x3","x4"), ...) { 
  opar <- par(mfrow = c(1, 2),pty="s",cex=0.8);  
  first <-  pca1$factor[,1];  second <-  pca1$factor[,2]
  plot(first, second,  type="n", xlim=c(-1.1,1.1),ylim=c(-1.1,1.1),
      main="因子負荷", cex=0.6)
  abline(h=0); abline(v=0)
  text(first, second, label=label,cex=0.8)
  z1 <- -1 * pca$Zstandard[,1]
  z2 <- -1 * pca$Zstandard[,2]
  plot(z1, z2, type="n", 
       main="(標準化)主成分スコア",cex=0.6)
       abline(h=0); abline(v=0)
  text(z1, z2, label=1:length(z1),cex=0.8)
} # end of pca.fig

par(family="Japan1")
pca.fig(pca1,label=colnames(df))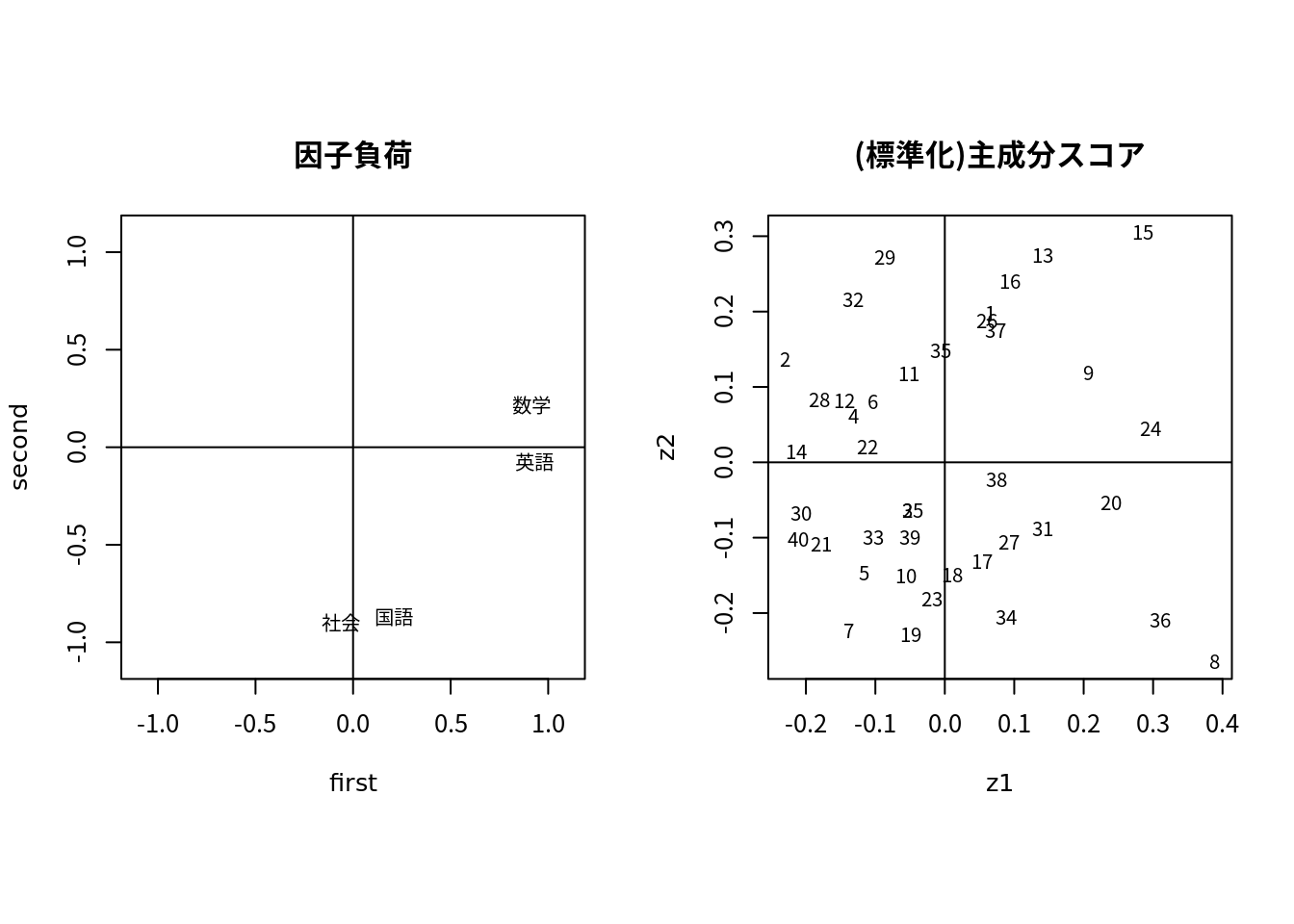

Z <- scale(df); Z[c(8,15,24,19),]

##            英語      数学       国語      社会
## [1,]  2.6363109  1.901342  0.9111062  2.328873
## [2,]  1.9339635  1.567187 -1.2030629 -2.045531
## [3,]  2.2349695  1.500356 -0.9010387  0.539344
## [4,] -0.6747551 -0.103588  1.3138050  1.334690

7.3 直線の当てはめ(最小2乗法)

直線の当てはめ問題をR言語を用いて処理する例を示す.関数lsfit()の出力の内の coefficients(回帰係数)より,モデル \(y = \beta_0 + \beta_1\,x\) の回帰係数 \(\beta_0=-3.4, \, \beta_1=2\) を得る.また,データ \((x,y)\) のプロット,回帰式の作図を示す.

x <- c(3,4,5,6,7)   # データｘ
y <- c(2,6,6,8,11)  # データｙ
out <- lsfit(x,y)   # 関数lsfit()を利用してy=b0+b1*x(直線)を当てはめる
str(out)            # 結果の簡略表示

## List of 4
##  $ coefficients: Named num [1:2] -3.4 2
##   ..- attr(*, "names")= chr [1:2] "Intercept" "X"
##  $ residuals   : num [1:5] -0.6 1.4 -0.6 -0.6 0.4
##  $ intercept   : logi TRUE
##  $ qr          :List of 6
##   ..$ qt   : num [1:5] -14.758 6.325 -0.138 0.309 1.757
##   ..$ qr   : num [1:5, 1:2] -2.236 0.447 0.447 0.447 0.447 ...
##   .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..$ : NULL
##   .. .. ..$ : chr [1:2] "Intercept" "X"
##   ..$ qraux: num [1:2] 1.45 1.12
##   ..$ rank : int 2
##   ..$ pivot: int [1:2] 1 2
##   ..$ tol  : num 1e-07
##   ..- attr(*, "class")= chr "qr"

out$coefficients    # 回帰係数のみを表示

## Intercept         X 
##      -3.4       2.0

plot(x,y)           # データ点(x,y)を作図
abline(out,col=2)   # 推定直線を赤(col=2)で表示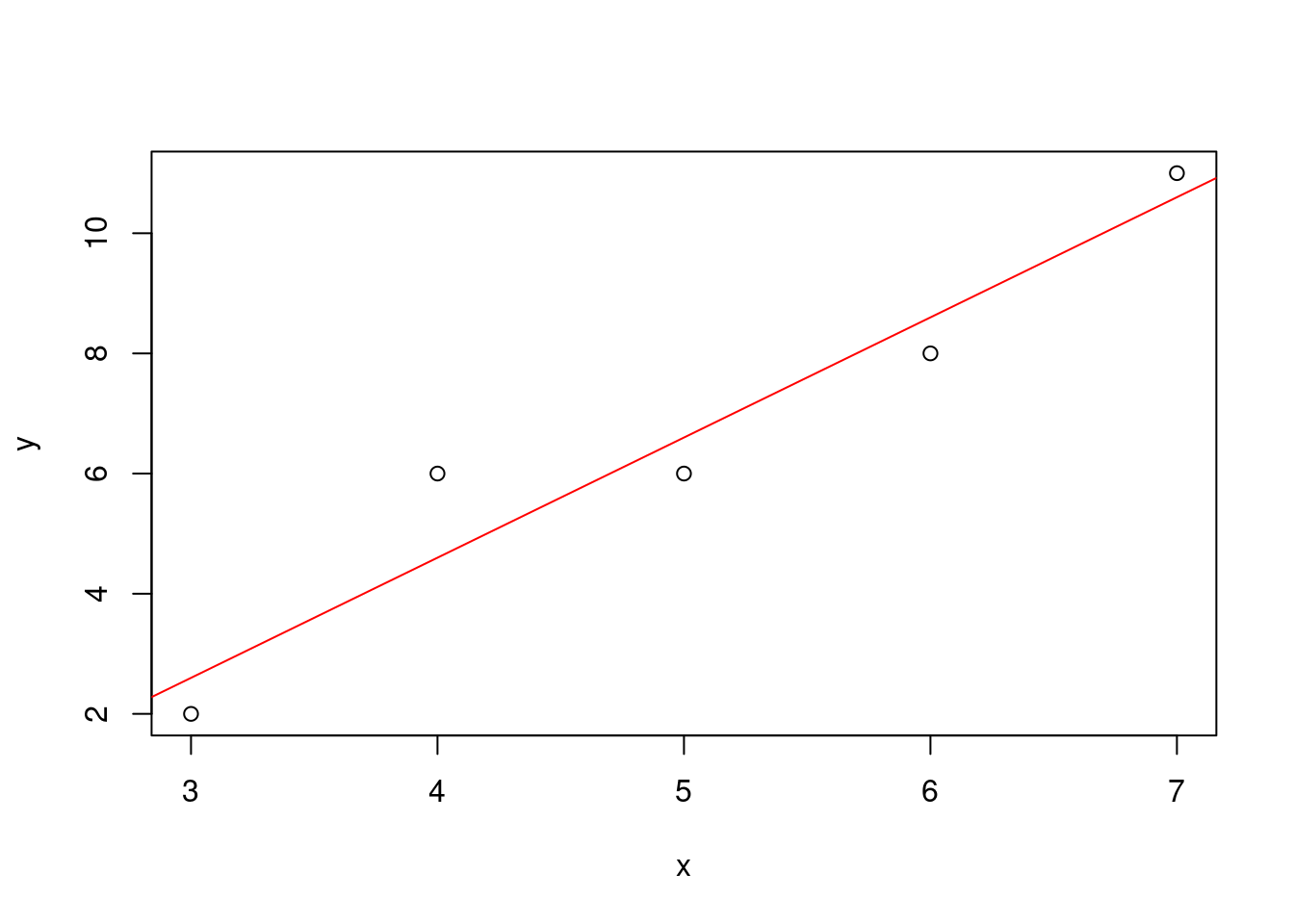

次に，原点を通る直線\(y = \beta_1 \,x\) を当てはめる場合の結果を示す．

out <- lsfit(x,y,intercept=FALSE)  # y=b1*x(原点を通る直線)を当てはめる
out$coefficients                   # 回帰係数のみを表示

##       X 
## 1.37037

plot(x,y,xlim=c(0,7),ylim=c(0,11)) # データ点(x,y)を作図
abline(out,col=2)                  # 推定直線を赤(col=2)で表示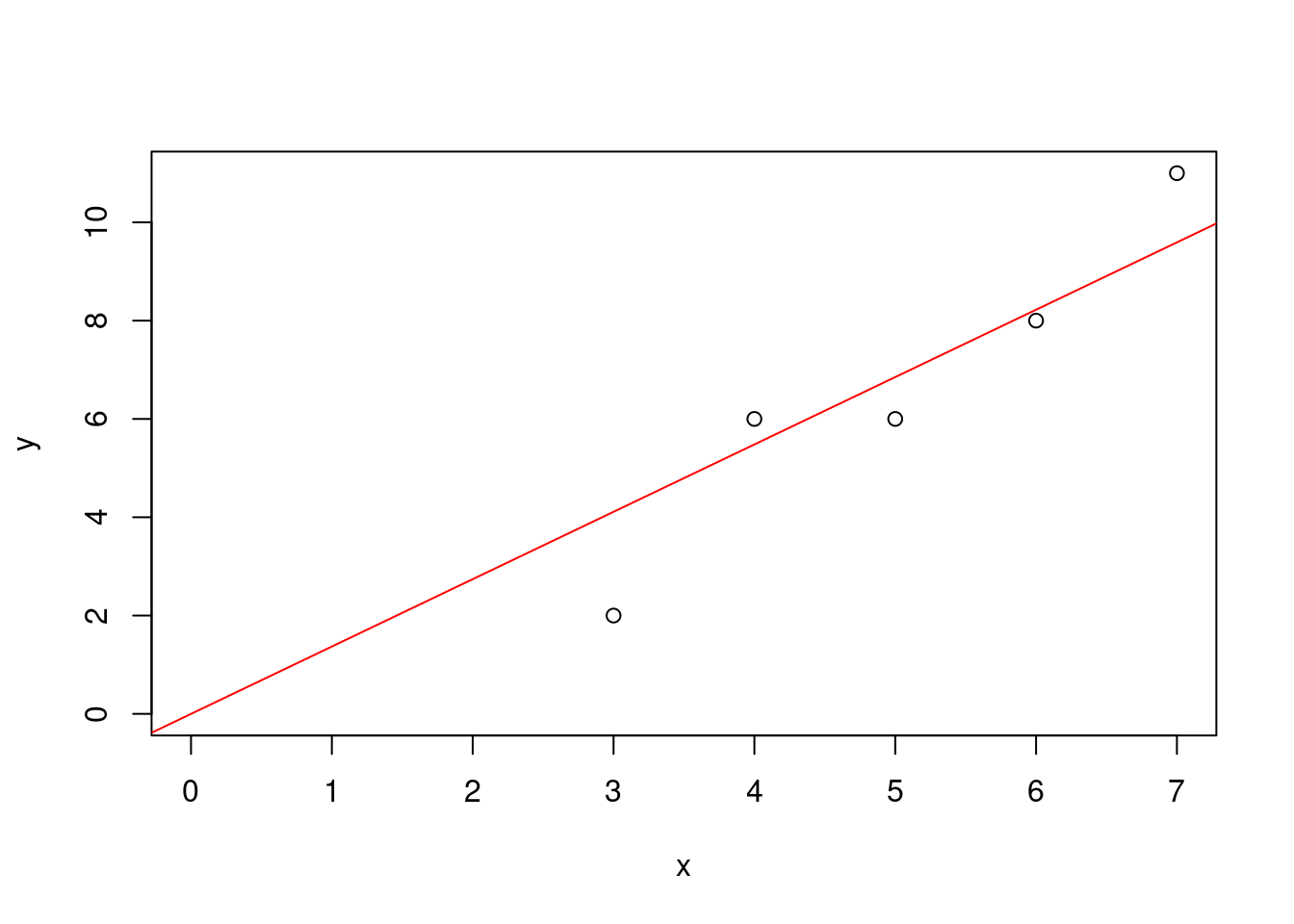

最後に，3次の多項式 \(y = \beta_0 + \beta_1\,x + \beta_2\,x^2 + \beta_3\,x^3\) を当てはめる場合の結果を示す．

X <- cbind(1,x,x^2,x^3) # 計画行列Xを作成(定数項を含む3次多項式)
out <- lsfit(X,y,intercept=F) # 線形モデル y = X b + e を当てはめる  
out$coefficients                       # 回帰係数のみを表示

##                       x                         
## -48.4000000  31.8333333  -6.2500000   0.4166667

yh <- X %*% out$coefficients  # データ点ｘでのｙの推定値
xg <- seq(x[1],x[length(x)],length=51) # 推定多項式の描画点の並び
Xg <- cbind(1,xg,xg^2,xg^3)            # 描画点に基づく計画行列
yhg <- Xg %*% out$coefficients         # 描画点における推定値の並び
plot(x,y)                              # テータ点(x,y)の描画
par(new=T)                             # 追加描画の設定
plot(xg,yhg,type="l",col=2,xlab="",ylab="",axes=F) # 推定多項式の描画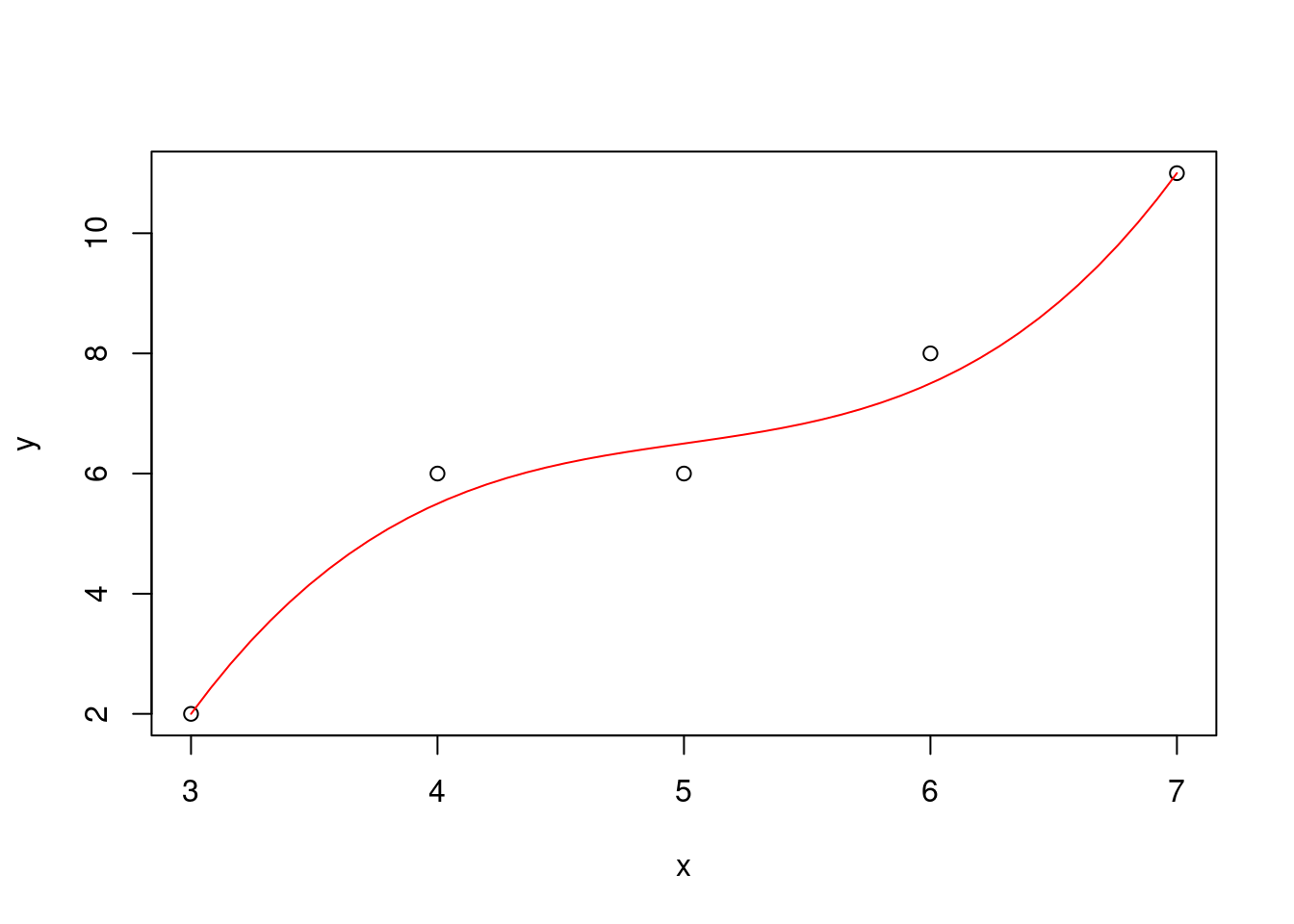

7.4 R言語から数式処理言語Maximaを実行する例

#--- R から Maxima を実行するR関数を作成 
rmaxima <- function(maxin){
  system("rm -f tmp-maxima-*")
  sink("tmp-maxima-in"); cat(maxin,"\n");   sink()
  system("max < tmp-maxima-in > out") 
       # maxima ではmaxima-init.macを読まない私的環境に設定されている為
  if (file.exists("tmp-maxima-out"))
    {source("tmp-maxima-out")
     print("File: tmp-maxima-out に出力された内容をR関数として取り込みました．")}
}
#--- Maxima 実行スクリプトの例 (この部分にMaximaプログラムを書く)
maxin <- paste(' \
 display2d:false$ \
 define(f(x,y), 2/3*x^2*y); \
 define(fx(x,y), diff(f(x,y),x))$ \
 t5 : taylor(sin(x),x,0,5); \  /* sin(x) をx=0において5次までTaylor展開する */
 define(t(x), t5)$ \
 /* 結果をRの関数として渡すMaxima私用関数rfuncout()を準備する */ 
 fundef(rfuncout); \   /* 結果が表示できない? */
 rfuncout("f","x,y", f(x,y), new)$ \  /* tmp-maxima-out に新規書き込み */
 rfuncout("fx","x,y", fx(x,y))$ \     /* 追記 */
 rfuncout("t","x",t(x))$ \            /* 追記 */
 quit();\
')
#--- 実行例
rmaxima(maxin)

## [1] "File: tmp-maxima-out に出力された内容をR関数として取り込みました．"

system("cat out")              #　非表示?
system("cat tmp-maxima-out")　　#　非表示?
f; f(2,1)

## function (x, y) 
## {
##     (2 * x^2 * y)/3
## }

## [1] 2.666667

fx; fx(2,1)

## function (x, y) 
## {
##     (4 * x * y)/3
## }

## [1] 2.666667

t # taylor(sin(x),x,0,5) をMaximaにより数式処理した結果をRの関数として受け取る

## function (x) 
## {
##     x - x^3/6 + x^5/120
## }

t(pi/10); sin(pi/10)

## [1] 0.3090171

## [1] 0.309017

curve(sin,xlim=c(-pi,pi),col="blue",lty=2,main="Taylor Expansion of sin(x)")
curve(t,xlim=c(-pi,pi),col="red",lty=1,add=T); abline(h=0); abline(v=0)
legend(1,-0.5,c("sin(x)","Taylor"),col=c("blue","red"),lty=c(2,1))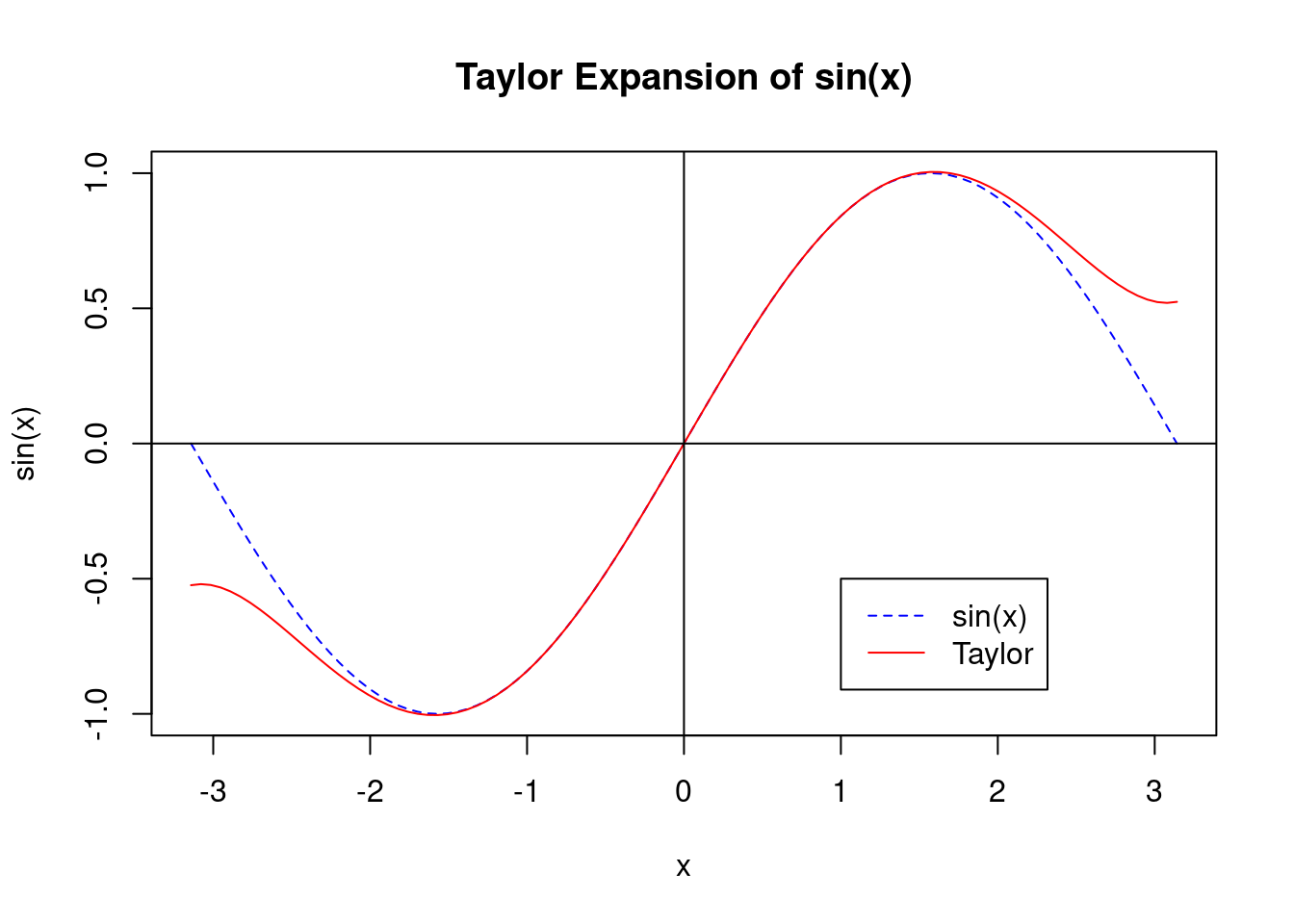

7.5 表のTeX表示

library(xtable)
tab <- matrix(1:6,2,3,byrow=T)
rownames(tab) <- c("row-1","row-2")
colnames(tab) <- c("col-1","col-2","col-3")
print(xtable(tab,digits=4,caption='tab1'))

## % latex table generated in R 3.6.3 by xtable 1.8-4 package
## % Sun Oct  4 15:01:05 2020
## \begin{table}[ht]
## \centering
## \begin{tabular}{rrrr}
##   \hline
##  & col-1 & col-2 & col-3 \\ 
##   \hline
## row-1 &     1 &     2 &     3 \\ 
##   row-2 &     4 &     5 &     6 \\ 
##    \hline
## \end{tabular}
## \caption{tab1} 
## \end{table}

8 続く

  Top   PageTop   PageEnd