Maxima レファレンス・マニュアル(暫定第3.3版)
INOUE Takakatsu 2024-05-15
索引
11. 数学関数
11.1 定数
Maximaに予約されている定数には,%e (自然対数の底 \(\doteq 2.718\)),%gamma (オイラー定数 \(\doteq 0.577\)), %phi (\(\frac{1+\sqrt{2}}{2} \doteq 1.618\)),%pi(円周率 \(\doteq 3.14\)),true(真),false (偽), inf(正の実無限大),minf (負の実無限大),infnity(複素無限大:任意の偏角で絶対値無限大)がある.また, 虚数単位は %i を用いる.
11.2 三角関数
Maxima には次の三角関数が用意されている.
- 三角関数と逆三角関数
| col1 | col2 | col3 | col4 |
|---|---|---|---|
| sin(x) | \(\sin(x)\) | asin(x) | \(\sin^{-1}(x)\) |
| cos(x) | \(\cos(x)\) | acos(x) | \(\cos^{-1}(x)\) |
| tan(x) | \(\tan(x) = \sin(x)/\cos(x)\) | atan(x) | \(\tan^{-1}(x)\) |
| atan2(y,x) | = atan(y/x) | ||
| sec(x) | \(\sec(x) = 1/\cos(x)\) | asec(x) | \(\sec^{-1}(x)\) |
| csc(x) | \(\csc(x) = 1/\sin(x)\) | acsc(x) | \(\csc^{-1}(x)\) |
| cot(x) | \(\cot(x) = 1/\tan(x)\) | acot(x) | \(\cot^{-1}(x)\) |
- 双曲線関数と逆双曲線関数
| col1 | col2 | col3 | col4 |
|---|---|---|---|
| sinh(x) | \(\sinh(x) = (e^x - e^{-x})/2\) | asinh(x) | \(\sinh^{-1}(x)\) |
| cosh(x) | \(\cosh(x) = (e^x + e^{-x})/2\) | acosh(x) | \(\cosh^{-1}(x)\) |
| tanh(x) | \(\tanh(x) = \sinh(x)/\cosh(x)\) | atanh(x) | \(\tanh^{-1}(x)\) |
| sech(x) | \({\rm sech}(x) = 1/{\rm cosh}(x)\) | asech(x) | \({\rm sech}^{-1}(x)\) |
| csch(x) | \({\rm csch}(x) = 1/{\rm sinh}(x)\) | acsch(x) | \({\rm csch}^{-1}(x)\) |
| coth(x) | \(\coth(x) = 1/\tanh(x)\) | acoth(x) | \(\coth^{-1}(x)\) |
また,\(\cos^2(x) + \sin^2(x) = 1\)
や \(\cos(2 x) = 2 \cos^2(x) - 1\)
等の恒等式は データベースとして用意されている.
三角関数に付随する関数は, 環境変数の trigexpand, trigreduce と trigsign
を参照する. 二つの share パッケージ(trigsimp, atrig1)は Maxima
に組み込みの簡約化の規則を拡張する.
11.2.1 予備知識
\[ \begin{array}{l} ◆ 弧度法: 0 \sim 2\pi \\ ◆ \sin\theta ~と~ \cos \theta ~の関係 : \\ ~~ \sin^2 \theta + \cos^2 \theta = 1,~~ ~~ \sin(\theta + \dfrac{\pi}{2}) = \cos \theta,~~ \cos(\theta + \dfrac{\pi}{2}) = -\sin \theta,~~\\ ~~ \sin(-\theta) = - \sin \theta ~~(奇関数),~~ \cos(-\theta) = \cos \theta ~~(偶関数)\\ ◆ 加法定理\\ ~~ \sin(\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ ~~ \sin(\alpha-\beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \\ ~~ \cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ ~~ \cos(\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\ ◆ 積を和・差になおす公式\\ ~~ \sin\alpha\cos\beta = \dfrac{1}{2}\left\{\sin(\alpha+\beta) + \sin(\alpha-\beta)\right\} \\ ~~ \cos\alpha\cos\beta = \dfrac{1}{2}\left\{\cos(\alpha+\beta) + \cos(\alpha-\beta)\right\} \\ ~~ \sin\alpha\sin\beta = \dfrac{1}{2}\left\{\cos(\alpha+\beta) - \cos(\alpha-\beta)\right\} ~~\\ ◆ 半角の公式\\ ~~\sin^2 \dfrac{\alpha}{2} = \dfrac{1}{2} (1- \cos \alpha) ~~\cos^2 \dfrac{\alpha}{2} = \dfrac{1}{2} (1+ \cos \alpha)\\ ~~\\ ◆ 三角関数の合成\\ ~~a\,\sin \theta + b \, \cos \theta = \sqrt{a^2+b^2}\, \sin(\theta + \alpha) \\ ~~ただし,~~ \cos \alpha = \dfrac{a}{\sqrt{a^2+b^2}}, \quad \sin \alpha = \dfrac{b}{\sqrt{a^2+b^2}}, \end{array} \]
11.2.2 三角関数の実行例
◇ 実行例の要約
(%i80) "------ 三角関数の実行例 ------"
(%i81) sin(%pi/3) ---> sqrt(3)/2
(%i82) asin(1) ---> %pi/2
(%i83) cos(acos(x)) ---> x
(%i84) acos(cos(x)) ---> x (主値に依存する)
(%i85) triginverses:true ---> true (default は all)
(%i86) cos(acos(x)) ---> x
(%i87) acos(cos(x)) ---> acos(cos(x))
三角関数の展開(trigexpand): sin(2*x) ---> 2 sin(x) cos(x)
(%i88) trigexpand(tan(y+x)) ---> (tan(y)+tan(x))/(1-tan(x)*tan(y))
(%i89) trigexpand(sin(%pi/3+x)) ---> sin(x)/2+sqrt(3)*cos(x)/2
(%i90) exp:trigexpand(cos(%pi/3+2*x))
(%o90) cos(2*x)/2-sqrt(3)*sin(2*x)/2
(%i91) trigexpand(exp)
(%o91) (cos(x)^2-sin(x)^2)/2-sqrt(3)*cos(x)*sin(x)
(%i92) ev(trigexpand(cos(%pi/3+2*x)),trigexpand:true)
trigexpand は標準では1回しか適用されないのでくり返し展開する
(%o92) (cos(x)^2-sin(x)^2)/2-sqrt(3)*cos(x)*sin(x)
三角関数の縮約(trigreduce): 2*sin(x)*cos(x) ---> sin(2 x)
(%i93) trigreduce(sin(x)^3) ---> (3*sin(x)-sin(3*x))/4
(%i94) trigrat(sin(%pi/6+2*x)^2) ---> (sqrt(3)*sin(4*x)-cos(4*x)+2)/4
(%i95) exp:trigexpand(sin(%pi/6+2*x)^2)
(%o95) (sqrt(3)*sin(2*x)/2+cos(2*x)/2)^2
(%i96) trigexpand(exp)
(%o96) ((cos(x)^2-sin(x)^2)/2+sqrt(3)*cos(x)*sin(x))^2
(%i97) exp:trigreduce(sin(%pi/6+2*x)^2)
(%o97) (1-cos(2*(2*x+%pi/6)))/2
(%i98) trigreduce(exp) ---> (1-cos(4*x+%pi/3))/2
(%i99) exp:trigrat(tan(x)) ---> sin(x)/cos(x)
(%i100) trigreduce(exp) ---> tan(x)
(%i101) exp:trigrat(tan(x)^3)
(%o101) -(sin(3*x)-3*sin(x))/(cos(3*x)+3*cos(x))
(%i102) exp1:trigreduce(exp)
(%o102) 3*sin(x)/(cos(3*x)+3*cos(x))-sin(3*x)/(cos(3*x)+3*cos(x))
(%i103) exp2:trigexpand(exp1)
(%o103) 3*sin(x)/(-3*cos(x)*sin(x)^2+cos(x)^3+3*cos(x))
-(3*cos(x)^2*sin(x)-sin(x)^3)
/(-3*cos(x)*sin(x)^2+cos(x)^3+3*cos(x))
(%i104) exp3:trigsimp(exp2) ---> sin(x)^3/cos(x)^3
(%i105) trigreduce(exp3) ---> tan(x)^3
(%i106) halfangles:true ---> true
(%i107) trigexpand(sin(x/2)^2) ---> (1-cos(x))/2
(%i108) halfangles:true ---> true
(%i109) trigexpand(cos(x/2)^2) ---> (cos(x)+1)/2
(%i110) halfangles:true ---> true
(%i111) exp1:trigexpand(tan(x/2)) ---> (1-cos(x))/sin(x)
(%i112) halfangles:true ---> true
(%i113) exp2:trigreduce(tan(x/2)) ---> (1-cos(x))*csc(x)
(%i114) maybe(equal(exp1,exp2)) ---> unknown応用例として三角関数の合成を行う関数を作成する.
◆ 実行例: 三角関数の合成
/home/inoue/bin/go tmp_lang/chunk-1.mx > tmp_lang/chunk-1.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-1.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-1.mx
display2d:false
trigcompose(exp,[args]):=block([tmp,w,a,b,r,t],w:trigexpand(exp),
a:coeff(w,sin(x)),b:coeff(w,cos(x)),r:sqrt(a^2+b^2),
if length(args) = 0 or args[1] = sin
then ("--- sin compose ---",
if a > 0
then (if b > 0 then t:acos(a/r) else t:asin(b/r))
else (if b > 0 then t:acos(a/r)
else t:asin((-b)/r)+%pi),ans:r*sin(x+t))
else ("--- cos compose ---",
if a > 0
then (if b > 0 then t:asin((-a)/r)
else t:asin(a/r)+%pi)
else (if b > 0 then t:asin((-a)/r)
else t:acos(b/r)),ans:r*cos(x+t)),
return(ans))
display2d:true
trigcompose((1/2)*sin(x)+(sqrt(3)/2)*cos(x))
%pi
sin(x + ---)
3
trigcompose((1/2)*sin(x)+(sqrt(3)/2)*cos(x),cos)
%pi
cos(x - ---)
6
/var/www/html/LANG/tmp_lang/chunk-1.mx11.2.3 三角関数に関連する環境変数
● halfangles:false
true であれば, \(\frac{\theta}{2}\)
に対して半角の公式が適用される.
● trigexpandplus:true
true であれば, 和の公式 (例えば,sin(x+y) が展開)が適用される.
● trigexpandtimes:true
true であれば, 積の公式 (例えば, sin(2*x) が展開)が適用される.
● triginverses:all
三角関数, 双曲関数とその逆関数との合成の簡約化を制御する.
all であれば, 例えば, atan(tan(x)) と tan(atan(x)) が共 に x
に簡約化される. true であれば, arcfunction(function(x)) は
簡易化されない.false であれば arcfunc(func)) と fun(arcfun(x))
は共に簡約化されない.
● trigsign:true
true であれば三角関数に対し負の引数の簡約化を許容する. 例えば,
trigsin が true のときに限り, sin(-x) は -sin(x) となる.
11.2.4 三角関数
● acos 逆余弦関数
● acosh 逆双曲線余弦関数
● acot 逆余接関数
● acoth 逆双曲線余接関数
● acsc 逆余割関数
● acsch 逆双曲線余割関数
● asec 逆正割関数
● asech 逆双曲線正割関数
● asin 逆正弦関数
● asinh 逆双曲線正弦関数
● atan 逆正接関数
● atan2
atan2(y,x) 区間 (-%pi,%pi) の間で atan(y/x) を計算する.
● atanh 逆双曲線正接関数
● cos 余弦関数
● cosh 双曲線余弦関数
● cot 余接関数
● coth 双曲線余接関数
● csc 余割関数
● csch 双曲線余割関数
● sec 正割関数
● sech 双曲線正割関数
● sin 正弦関数
● sinh 双曲線正弦関数
● tan 正接関数
● tanh 双曲線正接関数
● trigexpand(exp)
式expに現れる角度の和と角度の倍をもつ三角関数と双曲関数を展開する. この
関数は一度に一つのレベルのみの角度の和と角度の積の展開を行う.
sin と cos の全体の展開を直ちに得るためには, trigexpand:true;
を用いる.
◆ 実行例: trigexpand
/home/inoue/bin/go tmp_lang/chunk-2.mx > tmp_lang/chunk-2.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-2.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-2.mx
trigexpand(sin(x+%pi/6))
sqrt(3) sin(x) cos(x)
-------------- + ------
2 2
trigexpand(sin(2*x+%pi/6))
sqrt(3) sin(2 x) cos(2 x)
---------------- + --------
2 2
ev(x+sin(3*x)/sin(x),trigexpand = true,expand)
2 2
(- sin (x)) + 3 cos (x) + x
trigexpand(sin(10*x+y))
cos(10 x) sin(y) + sin(10 x) cos(y)
/var/www/html/LANG/tmp_lang/chunk-2.mx● trigreduce(exp, var)
三角関数の積と羃乗を結合する.
分母で現われたこれらの関数を消去することも試みる. なお,
変数varが省略されると, 式expの全ての変数varが利用される.
◆ 実行例: trigreduce
/home/inoue/bin/go tmp_lang/chunk-3.mx > tmp_lang/chunk-3.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-3.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-3.mx
trigreduce((-sin(x)^2)+3*cos(x)^2+x)
cos(2 x) cos(2 x) 1 1
-------- + 3 (-------- + -) + x - -
2 2 2 2
/var/www/html/LANG/tmp_lang/chunk-3.mx三角関数簡約化ルーチンは幾つかの単純な場合で宣言された情報を用いる. 変 数に関する宣言は次の様に使われる. 例えば,
◆ 実行例: 変数に関する宣言
/home/inoue/bin/go tmp_lang/chunk-4.mx > tmp_lang/chunk-4.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-4.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-4.mx
declare(j,integer,e,even,o,odd)
sin(x+(e+1/2)*%pi)
1
sin(x + %pi (e + -))
2
sin(x+(o+1/2)*%pi)
1
sin(x + %pi (o + -))
2
/var/www/html/LANG/tmp_lang/chunk-4.mx● trigsimp(exp)
tan, sec 等を含む式expの簡約化のために, 恒等式 \(\sin^2(x) + \cos^2(x) = 1\) と \(\cosh^2(x) − \sinh^2(x) = 1\)
を使って,
sin, cos, sinh, cosh へと変換する. trigreduce
と併用するとより進んだ簡約化が得られる場合がある.
◆ 実行例: trigsimp + trigreduce
/home/inoue/bin/go tmp_lang/chunk-5.mx > tmp_lang/chunk-5.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-5.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-5.mx
trigreduce(trigsimp((-sin(x)^2)+3*cos(x)^2+x))
cos(2 x) 1
4 (-------- + -) + x - 1
2 2
trigsimp(trigreduce((-sin(x)^2)+3*cos(x)^2+x))
2 cos(2 x) + x + 1
/var/www/html/LANG/tmp_lang/chunk-5.mx● trigrat(exp)
三角関数式expの簡約化を試みる.
◆ 実行例: trigrat
/home/inoue/bin/go tmp_lang/chunk-6.mx > tmp_lang/chunk-6.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-6.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-6.mx
"/* 注:以下の例を確かめる */"
c1:sin(3*a)/sin(a+%pi/3)
d1:trigrat(c1)
sqrt(3) sin(2 a) + cos(2 a) - 1
matchdeclare(a,true)
tellsimpafter(sin(a)^2,1-cos(a)^2)
expand(trigexpand(denom(c1)*d1-num(c1)))
3 2
sin (a) + cos (a) sin(a) - sin(a)
/var/www/html/LANG/tmp_lang/chunk-6.mx11.3 対数関数
\[ \begin{array}{ll} 指数関数:& y = a^x \quad (a : a >0 , a \neq 1)\\ 指数法則:& a^m\cdot a^n = a^{m+n},~~\dfrac{a^m}{a^n} = a^{m-n},~~ (a^m)^n = a^{m\cdot n} \\ 自然対数の底 e :& e = \displaystyle\lim_{n \rightarrow \pm \infty}\left(1+\dfrac{1}{n}\right)^n \doteq 2.72 \\ e^x の導関数:& (e^x)' = e^x\\ \end{array} \] \[ \begin{array}{l} 対数関数: y = \log_a x ~~\Longleftrightarrow~~ x = a^y \quad (a : a >0 , a \neq 1)\\ 自然対数: y = \log_e x = \log x \\ 底の変換公式: \log_a x = \dfrac{\log_c x}{\log_c a} \quad (a >0 , a \neq 1, c >0 , c \neq 1)\\ 対数法則\\ ~~ \log_a(xy) = \log_a x + \log_a y\\ ~~ \log \dfrac{x}{y} = \log_a x - \log_a y \\ ~~ \log_a x^c = c \log_a x \end{array} \]
11.3.1 対数関数に関連する環境変数
● %e_to_numlog:false
true であれば, r を有理数, x を式とすると, %e^(r*log(x)) が x^r
に簡約化される. なお, radcan 命令もこの変換を行なう.
● logabs:false
true であれば, integrate(1/x,x) の様に log
が結果に含まれる不定積分の結果は, log(abs(…)) の項をもつものとなる.
false であれば log(…) の項をもつものになる.
なお, 定積分の場合は, logabs:true が設定される. これは,
不定積分の両端点での評価が必要となることが多いためである.
● logarc:false
true であれば, 逆円関数 (逆三角関数),
逆双曲関数を対数関数の形式に変換する. logarc(式)
はこの環境変数の設定無しで, 特定の式に対し, ev
を用いた式の再評価を行なう.
● logconcoeffp:false
logcontract() を用いたときに log の内部に移される係数を制御する.
ここでは一つの引数の 関数の名前を設定する. 例えば, sqrt
を生成したい場合には,
◆ 実行例: logcontract
/home/inoue/bin/go tmp_lang/chunk-7.mx > tmp_lang/chunk-7.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-7.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-7.mx
display2d:false
logcontract((1/2)*log(x))
log(x)/2
logconcoeffp:'logconfun
logconfun(m):=featurep(m,integer) or ratnump(m)
logcontract((1/2)*log(x))
log(sqrt(x))
"/var/www/html/LANG/tmp_lang/chunk-7.mx"logcontract(1/2*log(x)); から log(sqrt(x)) が得られる.
● logexpand:true
true であれば, log(a^b) を blog(a) に変換する. all であれば,
log(ab) は log(a)+log(b) に変換される. super であれば, a=1
でない有理数 a/b に対し, log(a/b) は log(a) - log(b) となる (整数 b
に対して log(1/b) は常に簡約化される). false
であれば,これらの簡約化は全て実行されない.
● lognegint:false
true のとき, 正整数に対し, log(-n) を log(n)+%i*%pi
で置換える規則が内部的に設定される.
● lognumer:false
true のとき, log の負の浮動小数引数は log に渡される前に,
常にその絶対値に変換される. number が又 true であれば, log
の負の整数引数もその絶対値に変換される.
● logsimp:true
false のとき, log を含む %e の巾乗の自動簡約化が実行されない.
11.3.2 対数関数に関連する関数
● exp(x)
指数関数. 内部的には%e^x として表現されている.
● log(x)
自然対数関数
● logcontract(exp)
再帰的に式 exp を調べ, ‘a1log(b1) + a2log(b2) + c’
の形式の部分式を ‘log(ratsimp(b1^a1 * b2^a2)) + c’ に変換する.
◆ 実行例: logcontract
/home/inoue/bin/go tmp_lang/chunk-8.mx > tmp_lang/chunk-8.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-8.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-8.mx
2*(a*log(x)+2*a*log(y))
logcontract(%)
2 4
a log(x y )
/var/www/html/LANG/tmp_lang/chunk-8.mxdeclare(n,integer); を実行していれば, logcontract(2anlog(x)); は ‘alog(x^(2n))’ となる. この方法で潰される係数は, 上の例で示す様に 2 と n で, featurep(coeff, integer) を満す. 利用者は潰される 係数を, 1 引数の既に入力した関数の名前に対し, 環境変数の logconcoeffp を設定することで制御ができる. つまり, sqrt を生成したい場合, 以下の実行例のようにすれば, logcontract(1/2log(x)); は log(sqrt(x)) となる.
◆ 実行例:
rectform(z) ---> a + %i b
polarform(z) ---> r e^(%i t) = r (cos(t) + %i sin(t))
abs(z) ---> r
carg(z) ---> t
(%i115) "------ 複素数の実行例 ------"
(%i116) z0:%i+sqrt(3) ---> %i+sqrt(3)
(%i117) zp:polarform(z0) ---> 2*%e^(%i*%pi/6)
(%i118) abs(z0) ---> 2
(%i119) carg(z0) ---> %pi/6
(%i120) rectform(zp) ---> %i+sqrt(3)
(%i121) z1:r*(%i*sin(x)+cos(x)) ---> r*(%i*sin(x)+cos(x))
(%i122) z1abs:trigsimp(abs(z1)) ---> r
(%i123) z:z0*z1 ---> (%i+sqrt(3))*r*(%i*sin(x)+cos(x))
(%i124) trigsimp(z) ---> (sqrt(3)*%i-1)*r*sin(x)+(%i+sqrt(3))*r*cos(x)
(%i125) polarform(trigsimp(z)) ---<ダメ:以下の結果を返す>
(%o125) sqrt((sqrt(3)*r*sin(x)+r*cos(x))^2
+(sqrt(3)*r*cos(x)-r*sin(x))^2)
*%e^(%i*atan2(sqrt(3)*r*sin(x)+r*cos(x),
sqrt(3)*r*cos(x)-r*sin(x)))
(%i126) zarg:x+carg(z0%o42) ---> x+%pi/6
(%i127) zabs:abs(z0)*r ---> 2*r
(%i128) z:zabs*(%i*sin(zarg)+cos(zarg))
(%o128) 2*r*(%i*sin(x+%pi/6)+cos(x+%pi/6))● plog(x)
複素数値の自然対数関数の主分枝を −π < carg(x) <= π とする.
● polarform(exp)
式 exp を r%e^(%itheta) の形に変換する.
多項式が実数係数多項式の場合は入力のままで返され, 関数を含む場合には,
その関数が負であれば %e^{%i %pi} をかけたものが返される.
◆ 実行例: 極形式
/home/inoue/bin/go tmp_lang/chunk-9.mx > tmp_lang/chunk-9.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-9.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-9.mx
polarform((1+%i)^3)
3 %i %pi
--------
3/2 4
2 %e
polarform(x^2+1)
2
x + 1
assume(x+1 < 0)
polarform((x+1)^2)
2
((- x) - 1)
/var/www/html/LANG/tmp_lang/chunk-9.mx11.4 複素数と極形式
\[ オイラーの公式:\quad e^{i\,x} = \cos\,x + i\,\sin x \quad (x, \, 実数) \]
◇ 実行例要約
rectform(z) ---> a + %i b
polarform(z) ---> r e^(%i t) = r (cos(t) + %i sin(t))
abs(z)
---> r
carg(z)
---> t
(%i115) "------ 複素数の実行例 ------"
(%i116) z0:%i+sqrt(3)
---> %i+sqrt(3)
(%i117) zp:polarform(z0)
---> 2*%e^(%i*%pi/6)
(%i118) abs(z0)
---> 2
(%i119) carg(z0)
---> %pi/6
(%i120) rectform(zp)
---> %i+sqrt(3)
(%i121) z1:r*(%i*sin(x)+cos(x)) ---> r*(%i*sin(x)+cos(x))
(%i122) z1abs:trigsimp(abs(z1)) ---> r
(%i123) z:z0*z1
---> (%i+sqrt(3))*r*(%i*sin(x)+cos(x))
(%i124) trigsimp(z) ---> (sqrt(3)*%i-1)*r*sin(x)+(%i+sqrt(3))*r*cos(x)
(%i125) polarform(trigsimp(z)) ---< ダメ:以下の結果を返す >
(%o125) sqrt((sqrt(3)*r*sin(x)+r*cos(x))^2
+(sqrt(3)*r*cos(x)-r*sin(x))^2)
*%e^(%i*atan2(sqrt(3)*r*sin(x)+r*cos(x),
sqrt(3)*r*cos(x)-r*sin(x)))
(%i126) zarg:x+carg(z0%o42) ---> x+%pi/6
(%i127) zabs:abs(z0)*r
---> 2*r
(%i128) z:zabs*(%i*sin(zarg)+cos(zarg))
(%o128) 2*r*(%i*sin(x+%pi/6)+cos(x+%pi/6))11.5 その他の数学関数
区間定義関数
● charfun(cond)
区間毎に異なる式をもつ関数を定義するときに用いる.(数値的評価に限定される.)
◆ 実行例: charfun
/home/inoue/bin/go tmp_lang/chunk-10.mx > tmp_lang/chunk-10.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-10.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-10.mx
c(x):=charfun(x < 1)
c(x) := charfun(x < 1)
c(0)
1
c(1)
0
f(x):=f1(x)*charfun(x < 1)+f2(x)*charfun(x >= 1)
f(0)
f1(0)
f(1)
f2(1)
f(3)
f2(3)
"/* 以下は実行できない 2020-10-30 */"
g(x):=f1(x)*charfun('"and",(a <= x,x < b))
+f2(x)*charfun('"and",(b <= x,x < c))
g(0)
charfun: expected exactly 1 arguments but got 2: [and, 0 < b]
#0: g(x=0)
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-10.mx2項係数
● binomial(n,k)
2項係数 \({}_nC_k\) を与える.
◆ 実行例: binomial
/home/inoue/bin/go tmp_lang/chunk-11.mx > tmp_lang/chunk-11.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-11.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-11.mx
binomial(5,2)
10
/var/www/html/LANG/tmp_lang/chunk-11.mx連分数
● cf(exp)
exp を連分数に変換する.連分数 \(a + 1/(b +
1/(c+ \cdots))\) はリスト [a,b,c,…] で表現される. \(a, b, c, \cdots\)
は整数でなければならない.
● cfdisrep(list)
リスとによる連分数表現を一般表現に戻す.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-12.mx > tmp_lang/chunk-12.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-12.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-12.mx
d1:cf([1,2,3])
[1, 2, 3]
cfdisrep(d1)
1
1 + -----
1
2 + -
3
d2:cf([1,2,-3]+[1,-2,1])
[1, 1, 1, 2]
cfdisrep(d2)
1
1 + ---------
1
1 + -----
1
1 + -
2
/var/www/html/LANG/tmp_lang/chunk-12.mx● cflength:1
連分数展開の項の個数を制御する.
● cfexpand(x)
連分数表現 x の最後から1つ前と最後の分子と分母の行列を与える.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-13.mx > tmp_lang/chunk-13.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-13.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-13.mx
cflength:3
d1:cf(sqrt(3))
[1, 1, 2, 1, 2, 1, 2]
d2:cfexpand(d1)
[ 71 26 ]
[ ]
[ 41 15 ]
ev(d2[1,2]/d2[2,2],numer)
1.733333333333334
/var/www/html/LANG/tmp_lang/chunk-13.mx階乗関数
● factorial(n)
階乗関数 \(n!\) を返す.
● minfactorial(exp)
式 exp に異なった整数による階乗が存在するとき簡約化を行う.式 exp
に2項係数が含まれていれば,それを階乗の有理式に変換する.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-14.mx > tmp_lang/chunk-14.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-14.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-14.mx
d1:n!/(n+1)!
n!
--------
(n + 1)!
minfactorial(d1)
1
-----
n + 1
/var/www/html/LANG/tmp_lang/chunk-14.mx素数
● prime(n)
n 番目の素数を返す.(削除された関数?)
● primep(n)
n が素数なら true を返す.
● totient(n)
n と互いに素で n 以下の整数の個数を返す.
◆ 実行例: 素数
/home/inoue/bin/go tmp_lang/chunk-15.mx > tmp_lang/chunk-15.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-15.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-15.mx
prime(5)
prime(5)
primep(1)
false
primep(2)
true
primep(7)
true
totient(8)
4
/var/www/html/LANG/tmp_lang/chunk-15.mx乱数
● random_normal(mean,sd)
平均 mean, 標準偏差 sd のガウス分布(正規分布)に従う乱数を返す.
◆ 実行例: random_normal
/home/inoue/bin/go tmp_lang/chunk-16.mx > tmp_lang/chunk-16.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-16.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-16.mx
"/* 関数 gauss(0,1) は廃止された */"
gauss(0,1)
NOTE: The gauss function is superseded by random_normal in the `distrib' package.
Perhaps you meant to enter `random_normal(0,1)'.
done
load(distrib)
random_normal(0,1)
- 0.08535908220862701
random_normal(0,1)
- 0.1571112511759789
/var/www/html/LANG/tmp_lang/chunk-16.mx部分分数展開
● partfrac(exp, var)
式 exp を変数 var に関して部分分数展開する.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-17.mx > tmp_lang/chunk-17.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-17.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-17.mx
example(partfrac)
(%i1)
2/(x+2)-2/(x+1)+1/(x+1)^2
2 2 1
----- - ----- + --------
x + 2 x + 1 2
(x + 1)
(%i1)
ratsimp(%)
x
- -------------------
3 2
x + 4 x + 5 x + 2
(%i1)
partfrac(%,x)
2 2 1
----- - ----- + --------
x + 2 x + 1 2
(x + 1)
done
/var/www/html/LANG/tmp_lang/chunk-17.mx誤差関数 erf(x) に関して
◆ 実行例: (2022.02.14 改変)
/home/inoue/bin/go tmp_lang/chunk-18.mxl > tmp_lang/chunk-18.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-18.mxl")
read and interpret /var/www/html/LANG/tmp_lang/chunk-18.mxl
display2d:false
" /* F(x) = erf(x) の場合 */ "
define(F(x),erf(x))
define(f(x),diff(F(x),x))
Maxima encountered a Lisp error:
Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
Automatically continuing.
To enable the Lisp debugger set *debugger-hook* to nil.
c0show(f(x))
f(x) = f(x)
g01:gr2d(key = "f(x)",explicit(f(x),x,-4,4),grid = true,title = "f(x)=dF(x)/dx")
g02:gr2d(key = "F(x)",explicit(F(x),x,-4,4),grid = true,title = "F(x)=erf(x)")
draw(g01,g02,columns = 2,dimensions = [800,300],'terminal = 'png,
'file_name = "Max-ref-2_files/fig11-3")
draw2d (explicit): non defined variable in term: 'realpart(f(-3.7241379))
-- an error. To debug this try: debugmode(true);
"/var/www/html/LANG/tmp_lang/chunk-18.mxl"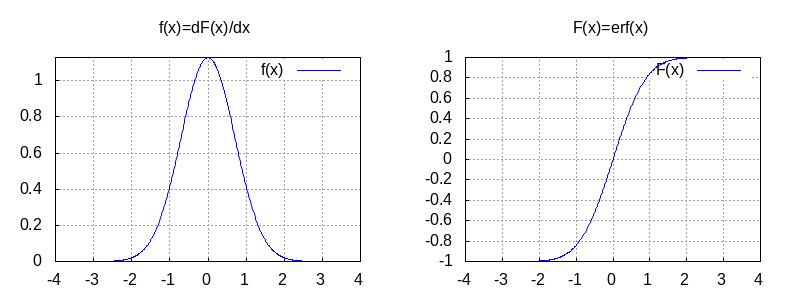
Graph of erf(x) 誤差関数
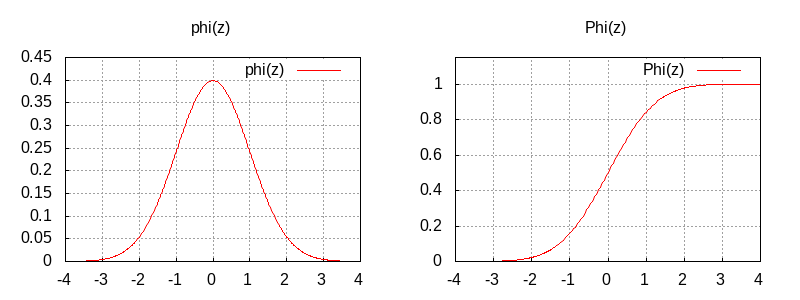
Graph of Phi(x) 標準正規分布の分布関数
erf(x) の導関数を \(f(x)\) とすると,標準正規分布の密度関数 \(\phi(z)\) との間に以下の関係式を得る. \(f(x) = \dfrac{2}{\sqrt{\pi}} \, e^{-x^2}\) において,変数変換 \(x = \dfrac{z}{\sqrt{2}}\) を行うと,\(\dfrac{dx}{dz} = \dfrac{1}{\sqrt{2}}\) より,変換後の関数は
\[ g(z) = f(x(z)) \, \cdot \, \dfrac{dx}{dz} =\dfrac{2}{\sqrt{\pi}} \,e^{-z^2/2}\, \cdot \, \dfrac{dx}{dz} = \dfrac{2}{\sqrt{\pi}} \,e^{-z^2/2}\, \cdot \, \dfrac{1}{\sqrt{2}} = 2 \times \phi(z) \] となることに注意する.よって,次式を得る. \[ \phi(z) = \dfrac{1}{2}\, f(x(z)) \, \cdot \, \dfrac{dx}{dz} = \dfrac{1}{2\sqrt{2}}\, f(x(z)) , \qquad x(z) = \dfrac{z}{\sqrt{2}} \] また,分布関数レベルでは,以下の関係式を得る. \[ \Phi(z) = \dfrac{F(x(z)) + 1}{2}, \qquad x(z) = \dfrac{z}{\sqrt{2}} \]
% %j[index](expr) 第 1 種 bessel 関数
% %k[index](expr) 第 2 種 bessel 関数
% %i[ ]( ) 変形 bessel 関数
% %he[ ]( ) エルミート多項式
% %p[ ]( ) ルジャンドル関数
% %q[ ]( ) 第 2 種ルジャンドル関数
% hstruve[ ]( ) struve の h 関数
% lstruve[ ]( ) struve の l 関数
% %f[ ]([],[],expr) 超幾何関数
% gamma() Γ関数
% gammagreek()
% gammaincomplete()
% slommel
% %m[]() 第 1 種の whittaker 関数
% %w[]() 第 2 種の whittaker 関数 11.6 特殊関数について
特殊関数に関する環境変数
● gammalim:1000000
整数と有理数引数に対するΓ関数の簡約化を制御する. 引数の絶対値が gammalim
よりも大きくなければ, 簡約化が 行われる. factlim スイッチは整数引数の
gamma の結果の簡約化も同様に制御することを挙げておく.
11.6.2 特殊関数に関する関数
● asymp
share1 ディレクトリにインストールされている feynman
図の漸近的な振舞いを見付けるプログラムのテスト版. より詳細な情報は
share1;asymp usage を参照 (漸近的解析関数に関しては asympa を参照).
● asympa
漸近的解析 - ファイル share1;asympa に漸近的解析向けの簡約化関数があり,
そこには広く複素解析や数値解析で 用いられている big-0 や little-o
関数も含まれている.batch(“asympa.mc”); を 実行せよ (feynman 図の
漸近的振舞いに関しては asymp を参照).
● bessel(z, a)
複素数 z と実数 a0 に対する bessel 関数 j の値を返す. 又, 配列
besselarray は besselarray[i]=ji+a-entier(a)
となる様に設定されている.
● beta(x, y)
gamma(x)*gamma(y)/gamma(x+y) と同じである.
● gamma(x)
Γ関数. 正整数に対しては gamma(i)=(i-1)!である. gammalim1000000 はガンマ関数の簡約化を制御する.
● makefact(式)
式の中の二項係数, ガンマ関数とベータ関数を階乗で置き換える.
● makegamma(式)
式 内の二項係数, 階乗, ベータ関数をガンマ関数で置き換える.
● numfactor(式)
積の式から数値の因数を取り出す. ここで, 式は単一項でなければならない.
和の中の全ての項の gcd が必要であれば,content 関数が使える.
/home/inoue/bin/go tmp_lang/chunk-19.mx > tmp_lang/chunk-19.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-19.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-19.mx
out:gamma(7/2)
15 sqrt(%pi)
------------
8
numfactor(out)
15
--
8
/var/www/html/LANG/tmp_lang/chunk-19.mx● poisexpt(a, b)
%b (正の整数) は機能的に intopois(a^b) と同一である.
● poismap(級数, sinfn , cosfn)
12. 式の操作
MAXIMA では,数,数式,文字式,等を一般に「式
(Expression)」として取り扱う. 例えば, 128, 1+2+3, a+b や sin(x) の様に,
数値, 変数といった複数の MAXIMA のアトムを演算子や関数
で結び付けたものを, 一般の式と見なす. ただし,
式は文脈で設定された各種の仮定や環境変数の指定に従って解釈される.
そのため, 上記の 1+2+3 を入力すると 6 が返されるが, a:sin(x) の場合は x
にどの様な値が割当てられてい るか,
或いは関連する環境変数の設定によって結果が異なる.
また,式は演算子を用いてリスト表現化される(第2節参照).
複数の式をコンマで区切って並べたものの全体を小括弧()で括ったものが式の列となる.
なお, MAXIMA 言語で生成した関数も実体は式の列である. そのため,
利用者定義関数もリスト処理関数による処理の対象となる. これは MAXIMA
が動作する LISP 側でも MAXIMA
言語による関数を操作出来ることを意味する.
本節では,単項式,多項式,一般の式に対する,展開,因子分解,等の操作について説明する.
12.1 多項式・一般式の操作一覧
一般表現とCRE表現の変換
rat(exp, var_1,...,var_k) 一般形式からCRE表現に変換する
ratdisrep(exp) CRE表現から一般形式に変換する
totaldisrep(exp) CRE表現から一般形式に変換する
多項式に関する述語関数
ratnump(exp) exp が有理数の場合に true を返す
ratp(exp) exp が拡張CRE表現の場合に true を返す
多項式の係数を取り出す関数
coeff(exp,var,n) exp 内で var^n の係数を返す(意味を考慮しない)
ratcoef(exp_1,exp_2,n) exp_1 内で exp_2^n の係数を返す(意味を考慮して)
ratcoef(exp_1,exp_2) exp_1 内で exp_2^1 の係数を返す(意味を考慮して)
bothcoef(exp,var)
式の展開に関する関数
expand(exp,p,n) exp を展開する
expand(exp) exp を展開する
expandwrt(exp,var_1,var_2,...)
expandwrt_factored(exp,var_1,var_2,...)
項数や次数を返す関数
nterms(exp) exp の展開形の項数を返す
powers(exp,var) exp の var に関する次数リスとを返す
多項式の項の次数を返す関数
hipow(poly,var) poly の var に関する見かけの最高次数を返す
lopow(poly,var) poly の var に関する見かけの最低次数を返す
多項式の変数の順序に関する関数
ratvars(var_1,var_2,...,var_k) 変数の順序を与える
showratvars(exp) 変数順序を表示する
多項式をまとめる関数
factcomb(exp) exp 内の階乗関数を簡約化する
rootscontract(exp) 有理式 exp の巾同士の積を簡約化する 有理式(の分子,分母)に関連する関数
combine(exp) 共通分母にする
denom(wxp) 有理式の分母を返す
num(exp) 有理式の分子を返す
ratdenom(exp) 有理式の分母を返す
ratnumer(exp) 有理式の分子を返す
ratdiff(exp,var) 有理式を微分する
共通因子を求める関数
gcd(exp_1,exp_2,var_1,...) exp_1 と exp_2 の最大公約因子を返す
gcde(poly_1,poly_2,var) c = a*poly1 + b*ploy2 となる[a,b,c]を返す
gcdex(poly_1,poly_2) exp_1 と exp_2 の最大公約因子を返す
gcfactor(poly) ploy の因子分解を返す
gfactorsum(poly) gfactor による因子分解を返す
ezgcd(poly_1,poly_2,...) poly_1/poly_2 の商と余りをリストで返す
content(poly,var_1,var_2,...) ploly を簡約化(共通因子の括り出し)する
因子分解を行う関数
dontfactor:[] 因子分解から除外する変数を指定する
factor(exp) 因子分解を返す
factor(exp,p) 最小多項式がpの因子分解を行う
factorsum(exp) グループ単位の因子分解を試みる
sqfr(exp)
factorout(exp,var_1,var_2,...) exp=f(var_1,...)*g にまとめる
nthroot(poly, n) 結果のn乗がpolyとなる結果を返す
剰余を求める関数
divide(poly_1,poly_2,var_1,var_2,...) poly_1/poly_2 の剰余を返す
quotient(poly_1,poly_2,var_1,var_2,...) poly_1/poly_2 をリストで返す
remainder(poly_1,poly_2,var_1,var_2,...) poly_1/poly_2 の剰余を返す
mod(poly,n) poly/n の剰余を返す
CRE表現の簡約化に関連する関数
ratexpand(exp) exp が多項式なら展開,有理式なら簡約化を行う
fullratsimp(exp,var_1,var_2,...) exp の簡約化を繰り返す
fullratsimp(exp,n) exp の簡約化を繰り返す
ratsimp(exp) exp の簡約化を行う
ratsimp(exp,var_1,var_2,...) exp の簡約化を行う 変数の述語関数
freeof(var_1,...,var_k,exp) expがvar_1,..に依存しないときtrueを返す
変数に関する操作
values 付値された変数一覧を表示
remvalue(var_1,var_2,...) 変数から付置属性を削除する
remvalue(all) 全ての変数から付置属性を削除する
args(exp) exp が関数なら引数個数,リストなら要素数を返す
listofvars(exp) exp に含まれる変数をリストで返す
isolate(exp,var) exp から var を孤立させる
disolate(exp,var_1,var_2,...) exp から var_1,... を孤立させる
部分式に分解する関数
parttition(exp,var) exp から var を含む部分と他部分に分解する
rectform(exp) 複素数 exp を実部,虚数部に分解する
部分式を取り出す関数
inpart(exp,n_1,n_2,...) exp の内部表現に対して部分を取り出す
inpart(exp,[n_1,n_2,...]) exp の内部表現に対して部分を取り出す
part(exp,n_1,n_2,...) exp に対して部分を取り出す
part(exp,[n_1,n_2,...]) exp に対して部分を取り出す
pickpart(exp,n) n 指定された階層の部分式を返す
pice 部分式を一次保存する変数
partswitch:false
式の最適化
optimize(exp) exp の最適化を行う
式への代入(置換)
subst(new,old,exp) exp に含まれるサブ式 old を new に置換する
ratsubst(new,old,exp) exp に含まれるサブ式 old を new に置換する
sublis(list,exp) 置換規則をリストで与えるときに用いる
substpart(new,exp,n_1,n_2,...) expのn1,.で指定された部分をnewで置換する
substinpart(new,exp,n_1,n_2,...) 内部表現に対して行う
指数関数の表示
demoivre:false 指数関数の表示を制御する
exponentialize:false exp を指数関数形式に変換する
演算子の分配に関する関数
distrib(exp)
multthru(exp_1,exp_2) exp_2 の各項を exp_1 倍する
multthru(exp) exp の部分展開を行う
総和と積
product(exp,var,lo,hi) 総積関数
sum(exp,var,lo,hi) 総和関数
総和関数の簡約化
sumcontract(exp) 総和関数の簡約化を試みる
intosum(exp) 積の項を総和関数の中に入れる
簡約化を行う関数
radcan(exp) 指数,対数,巾を含む式 exp の簡約化を試みる
scsimp(exp,rule_1,rule_2,...) 規則を考慮した簡約化を試みる
式の各項毎の簡約化
map() 各項毎に部分分数展開する
map(ratsimp,exp) 各項毎にratsimp()を作用する12.2 多項式・一般式の操作例
一般表現とCRE表現の変換
rat(exp, var_1,...,var_k) 一般形式からCRE表現に変換する
ratdisrep(exp) CRE表現から一般形式に変換する
totaldisrep(exp) CRE表現から一般形式に変換する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-20.mx > tmp_lang/chunk-20.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-20.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-20.mx
ex0:(x-2*y)^4/(x^2-4*y^2)^2+1
4
(x - 2 y)
------------ + 1
2 2 2
(x - 4 y )
d0:rat(ex0,y,x)
2 2
2 x + 8 y
/R/ -----------------
2 2
x + 4 y x + 4 y
ex:(((x-2*y)^4/(x^2-4*y^2)^2+1)*(y+a)*(2*y+x))/(4*y^2+x^2)
4
(x - 2 y)
(y + a) (2 y + x) (------------ + 1)
2 2 2
(x - 4 y )
------------------------------------
2 2
4 y + x
d1:rat(ex,y,a,x)
2 a + 2 y
/R/ ---------
x + 2 y
d2:ratdisrep(d1)
2 y + 2 a
---------
2 y + x
d3:totaldisrep(d1)
2 y + 2 a
---------
2 y + x
/var/www/html/LANG/tmp_lang/chunk-20.mx\[ \frac{\left(1 + \frac{(x-2y)^4}{(x^2-4y^2)^2}\right)\,(y+a)(2y+x)}{x^2 + 4y^2} = \frac{2(x^2+4y^2)}{(x+2y)^2} \times \frac{(y+a)(2y+x)}{x^2 + 4y^2} = \frac{2(y+a)}{x+2y} \]
多項式に関する述語関数
ratnump(exp) exp が有理数の場合に true を返す
ratp(exp) exp が拡張CRE表現の場合に true を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-21.mx > tmp_lang/chunk-21.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-21.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-21.mx
c1:2/3
ratnump(c1)
true
c2:(x+a)/(x+b)
ratp(c2)
false
ratp(rat(c2))
true
/var/www/html/LANG/tmp_lang/chunk-21.mx多項式の係数を取り出す関数
coeff(exp,var,n) exp 内で var^n の係数を返す(意味を考慮しない)
ratcoef(exp_1,exp_2,n) exp_1 内で exp_2^n の係数を返す(意味を考慮して)
ratcoef(exp_1,exp_2) exp_1 内で exp_2^1 の係数を返す(意味を考慮して)
bothcoef(exp,var) CRE表現式 exp の var の係数部分を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-22.mx > tmp_lang/chunk-22.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-22.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-22.mx
coeff(2*a*tan(x)+tan(x)+b = 5*tan(x)+3,tan(x))
2 a + 1 = 5
coeff(y+x*%e^x+1,x,0)
y + 1
ratcoef(a*x+b*x+5,a+b)
x
bothcoef(rat(a*x+b*x+5),x)
/R/ [b + a, 5]
/var/www/html/LANG/tmp_lang/chunk-22.mx式の展開に関する関数
expand(exp,p,n) exp を展開する
expand(exp) exp を展開する
expandwrt(exp,var_1,var_2,...)
expandwrt_factored(exp,var_1,var_2,...)◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-23.mx > tmp_lang/chunk-23.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-23.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-23.mx
d1:expand((a+b)^3)
3 2 2 3
b + 3 a b + 3 a b + a
factor(d1)
3
(b + a)
/var/www/html/LANG/tmp_lang/chunk-23.mx項数や次数を返す関数
nterms(exp) exp の展開形の項数を返す
powers(exp,var) exp の var に関する次数リスとを返す(警告)◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-24.mx > tmp_lang/chunk-24.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-24.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-24.mx
nterms((x+1)^2)
3
nterms(sin(x+1)^2)
1
/var/www/html/LANG/tmp_lang/chunk-24.mx多項式の項の次数を返す関数
hipow(poly,var) poly の var に関する見かけの最高次数を返す
lopow(poly,var) poly の var に関する見かけの最低次数を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-25.mx > tmp_lang/chunk-25.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-25.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-25.mx
hipow(y^3*x^2+x*y^4,x)
2
hipow((x+y)^5,x)
1
hipow(expand((x+y)^5),x)
5
hipow((x+y)^5,x+y)
5
hipow(expand((x+y)^5),x+y)
0
lopow(y^3*x^2+x*y^4,x)
1
/var/www/html/LANG/tmp_lang/chunk-25.mx多項式の変数の順序に関する関数
ratvars(var_1,var_2,...,var_k) 変数の順序を与える
showratvars(exp) 変数順序を表示する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-26.mx > tmp_lang/chunk-26.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-26.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-26.mx
ratvars(x,y,z)
d1:rat(x+y+z)
/R/ z + y + x
d2:rat(x+y+z+a)
/R/ z + y + x + a
ratvars(z,y,x)
d3:rat(x+y+z+a)
/R/ x + y + z + a
showratvars(d3)
[a, z, y, x]
/var/www/html/LANG/tmp_lang/chunk-26.mx多項式をまとめる関数
factcomb(exp) exp 内の階乗関数を簡約化する
rootscontract(exp) 有理式 exp の巾同士の積を簡約化する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-27.mx > tmp_lang/chunk-27.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-27.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-27.mx
factcomb((n+1)*n!)
(n + 1)!
rootscontract(x^(1/2)*y^(3/2))
3
sqrt(x y )
/var/www/html/LANG/tmp_lang/chunk-27.mx有理式(の分子,分母)に関連する関数
combine(exp) 共通分母にする
denom(wxp) 有理式の分母を返す
num(exp) 有理式の分子を返す
ratdenom(exp) 有理式の分母を返す
ratnumer(exp) 有理式の分子を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-28.mx > tmp_lang/chunk-28.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-28.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-28.mx
display2d:false
combine(1/(x-a)+1/(x-a))
2/(x-a)
combine(1/(x-a)+1/(x-b))
1/(x-b)+1/(x-a)
denom((x-a)/(x-b))
x-b
num((x-a)/(x-b))
x-a
ratdenom((x-a)/(x-b))
x-b
ratnumer((x-a)/(x-b))
x-a
"/var/www/html/LANG/tmp_lang/chunk-28.mx"共通因子を求める関数
gcd(exp_1,exp_2,var_1,...) exp1 と exp2 の最大公約因子を返す
gcde(poly_1,poly_2,var) c = a*poly1 + b*ploy2 となる[a,b,c]を返す
gcdex(poly_1,poly_2) exp1 と exp2 の最大公約因子を返す
gcfactor(poly) ploy の因子分解を返す
gfactorsum(poly) gfactor による因子分解を返す
ezgcd(poly_1,poly_2,...) poly1/poly2 の商と余りをリストで返す
content(poly,var_1,var_2,...) ploly を簡約化(共通因子の括り出し)する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-29.mx > tmp_lang/chunk-29.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-29.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-29.mx
display2d:false
gcd(x^2-1,x+1)
x+1
gcdex(x^2-1,x+1)
[0,1,x+1]
gcdex(x*(y+1),y^2-1,y)
[1,0,x*y+x]
gcfactor(1+5*%i)
(1+%i)*(3+2*%i)
gfactor(x^4-1)
(x-1)*(x+1)*(x-%i)*(x+%i)
factor(x^4-1)
(x-1)*(x+1)*(x^2+1)
gfactorsum(x^2+1)
(x-%i)*(x+%i)
factor(x^2+1)
x^2+1
ezgcd(x^2+2*x+3,x-1)
[1,x^2+2*x+3,x-1]
content(x^2+3*x+2,x)
[1,x^2+3*x+2]
content(a*x^2+3*a*x+2*a,x)
[a,x^2+3*x+2]
"/var/www/html/LANG/tmp_lang/chunk-29.mx"因子分解を行う関数
dontfactor:[] 因子分解から除外する変数を指定する
factor(exp) 因子分解を返す
factor(exp,p) 最小多項式がpの因子分解を行う
factorsum(exp) グループ単位の因子分解を試みる
sqfr(exp)
factorout(exp,var_1,var_2,...) exp=f(var1,...)*g にまとめる
nthroot(poly, n) 結果のn乗がpolyとなる結果を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-30.mx > tmp_lang/chunk-30.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-30.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-30.mx
display2d:false
factor(2^63-1)
7^2*73*127*337*92737*649657
factor((-8)*y-4*x+z^2*(2*y+x))
(2*y+x)*(z-2)*(z+2)
ex:(-1)-2*x-x^2+y^2+2*x*y^2+x^2*y^2
block([dontfactor:[x]],factor((ex/36)/(1+2*y+y^2)))
((x^2+2*x+1)*(y-1))/(36*(y+1))
sqfr(4*x^4+4*x^3+(-3)*x^2+(-4)*x-1)
(2*x+1)^2*(x^2-1)
factorout(expand((x+y)^2*(z+a)),x,y)
(y+x)^2*z+a*(y+x)^2
nthroot(expand((x+1)^3),3)
x+1
"/var/www/html/LANG/tmp_lang/chunk-30.mx"剰余を求める関数
divide(poly_1,poly_2,var_1,var_2,...) poly1/poly2 の剰余を返す
quotient(poly_1,poly_2,var_1,var_2,...) poly1/poly2 をリストで返す
remainder(poly_1,poly_2,var_1,var_2,...) poly1/poly2 の剰余を返す
mod(poly,n) poly/n の剰余を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-31.mx > tmp_lang/chunk-31.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-31.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-31.mx
divide(x+y,x-y,x)
[1, 2 y]
divide(x+y,x-y)
[- 1, 2 x]
quotient(x+y,x-y,x)
1
quotient(x+y,x-y)
- 1
remainder(x+y,x-y,x)
2 y
remainder(x+y,x-y)
2 x
mod(2^3,5)
3
/var/www/html/LANG/tmp_lang/chunk-31.mx\[ \frac{x+y}{x-y} = \frac{(x-y)+2y}{x-y} = 1 + \frac{2y}{x-y} \] \[ \frac{x+y}{x-y} = - \frac{y+x}{y-x} = - \frac{(y-x)+2x}{y-x} = -1 + \frac{2x}{x-y} \]
CRE表現の簡約化に関連する関数
ratexpand(exp) exp が多項式なら展開,有理式なら簡約化を行う
fullratsimp(exp,var_1,var_2,...) exp の簡約化を繰り返す
fullratsimp(exp,n) exp の簡約化を繰り返す
ratsimp(exp) exp の簡約化を行う
ratsimp(exp,var_1,var_2,...) exp の簡約化を行う◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-32.mx > tmp_lang/chunk-32.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-32.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-32.mx
display2d:false
ratexpand((2*x-3*y)^3)
(-27*y^3)+54*x*y^2-36*x^2*y+8*x^3
expr:(x-1)/(x+1)^2+1/(x-1)
expand(expr)
x/(x^2+2*x+1)-1/(x^2+2*x+1)+1/(x-1)
ratexpand(expr)
(2*x^2)/(x^3+x^2-x-1)+2/(x^3+x^2-x-1)
expr:((x^(a/2)+1)^2*(x^(a/2)-1)^2)/(x^a-1)
ratsimp(expr)
(x^(2*a)-2*x^a+1)/(x^a-1)
fullratsimp(expr)
x^a-1
"/var/www/html/LANG/tmp_lang/chunk-32.mx"変数の述語関数
freeof(var_1,...,var_k,exp) exp が var_1,... に依存しないとき true を返す◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-33.mx > tmp_lang/chunk-33.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-33.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-33.mx
display2d:false
freeof(c,(a+b)^3)
true
c:a
freeof(c,(a+b)^3)
false
kill(c)
freeof(a+b,(a+b)^3)
false
freeof(a+b,expand((a+b)^3))
true
"/var/www/html/LANG/tmp_lang/chunk-33.mx"変数に関する操作
values 付値された変数一覧を表示
remvalue(var_1,var_2,...) 変数から付置属性を削除する
remvalue(all) 全ての変数から付置属性を削除する
args(exp) exp が関数なら引数個数,リストなら要素数を返す
listofvars(exp) exp に含まれる変数をリストで返す
isolate(exp,var) exp から var を孤立させる
disolate(exp,var_1,var_2,...) exp から var_1,... を孤立させる◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-34.mx > tmp_lang/chunk-34.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-34.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-34.mx
display2d:false
kill(all)
(a:1,b:sin(a),values)
[a,b]
remvalue(a)
[a]
values
[b]
remvalues(all)
values
[b]
args(f(x,y))
[x,y]
args(sin(x+y))
[y+x]
args(sin(x+y)^2)
[sin(y+x),2]
listofvars(f(x,y))
[x,y]
listofvars(sin(x+y))
[x,y]
listofvars(sin(x+y)^2)
[x,y]
isolate(expand((1+a+x)^2),x)
a^2+2*a+1
x^2+2*a*x+2*x+%t12
isolate_wrt_times:true
isolate(expand((1+a+x)^2),x)
2*a
x^2+%t14*x+2*x+%t12
disolate(expand((1+a+x)^2),x)
x^2+%t14*x+2*x+%t12
"/var/www/html/LANG/tmp_lang/chunk-34.mx"部分式に分解する関数
parttition(exp,var) exp から var を含む部分と他部分に分解する
rectform(exp) 複素数 exp を実部,虚数部に分解する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-35.mx > tmp_lang/chunk-35.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-35.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-35.mx
display2d:false
partition(x+a,x)
[a,x]
partition((x+a)*y,x)
[y,x+a]
partition([x+a,y],x)
[[y],[x+a]]
rectform((x+%i)^2)
x^2+2*%i*x-1
"/var/www/html/LANG/tmp_lang/chunk-35.mx"部分式を取り出す関数
inpart(exp,n_1,n_2,...) exp の内部表現に対して部分を取り出す
inpart(exp,[n_1,n_2,...]) exp の内部表現に対して部分を取り出す
part(exp,n_1,n_2,...) exp に対して部分を取り出す
part(exp,[n_1,n_2,...]) exp に対して部分を取り出す
pickapart(exp,n) n 指定された階層の部分式を返す
pice 部分式を一次保存する変数
partswitch:false◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-36.mx > tmp_lang/chunk-36.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-36.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-36.mx
display2d:false
part((x+1)^3+2,1)
(x+1)^3
part((x+1)^3+2,1,1)
x+1
ex1:x+y+sin(x)+cos(y)
part(ex1,0)
"+"
part(ex1,1)
cos(y)
part(ex1,[1,4])
cos(y)+x
inpart(ex1,0)
"+"
inpart(ex1,1)
x
inpart(ex1,[1,4])
cos(y)+x
ex2:x*y*sin(x)*cos(y)
part(ex2,0)
"*"
part(ex2,1)
x
inpart(ex2,0)
"*"
inpart(ex2,1)
x
ex3:(x+1)^2
pickapart(ex3,1)
x+1
%t18^2
pickapart(expand(ex3),1)
x^2
2*x
%t20+%t19+1
"/var/www/html/LANG/tmp_lang/chunk-36.mx"式の最適化
optimize(exp) exp の最適化を行う◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-37.mx > tmp_lang/chunk-37.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-37.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-37.mx
display2d:false
ex:(x+1)^2+1/(x+1)^2+exp((x+1)^2)
optimize(ex)
block([%1],%1:(x+1)^2,%e^%1+%1+1/%1)
"/var/www/html/LANG/tmp_lang/chunk-37.mx"式への代入(置換)
subst(new,old,exp) exp に含まれるサブ式 old を new に置換する
ratsubst(new,old,exp) exp に含まれるサブ式 old を new に置換する
sublis(list,exp) 置換規則をリストで与えるときに用いる
substpart(new,exp,n_1,n_2,...) expのn_1,.で指定された部分をnewで置換する
substinpart(new,exp,n_1,n_2,...) 内部表現に対して行う◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-38.mx > tmp_lang/chunk-38.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-38.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-38.mx
display2d:false
subst(a,x+y+z,2*(x+y+z)*w)
2*a*w
subst(a,x+y,2*(x+y+z)*w)
2*w*(z+y+x)
ratsubst(a,x*y^2,x^4*y^3+x^4*y^8)
a*x^3*y+a^4
ratsubst(1-cos(x)^2,sin(x)^2,sin(x)^4)
cos(x)^4-2*cos(x)^2+1
sublis([a = b,b = a],sin(a)+cos(b))
sin(b)+cos(a)
substpart(3/2,1/(x^2+2),2,1,2)
1/(x^(3/2)+2)
substpart("+",a*x+f(b,y),1,0)
x+f(b,y)+a
substinpart(f1,f[1](x+1),0)
f1(x+1)
"/var/www/html/LANG/tmp_lang/chunk-38.mx"指数関数の表示
demoivre:false 指数関数の表示を制御する
exponentialize:false exp を指数関数形式に変換する◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-39.mx > tmp_lang/chunk-39.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-39.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-39.mx
display2d:false
exp(a+b*%i)
%e^(%i*b+a)
demoivre
false
demoivre:true
exp(a+b*%i)
%e^a*(%i*sin(b)+cos(b))
exp(polarform(a+b*%i))
%e^a*(%i*sin(b)+cos(b))
"/var/www/html/LANG/tmp_lang/chunk-39.mx"演算子の分配に関する関数
distrib(exp)
multthru(exp_1,exp_2) exp_2 の各項を exp_1 倍する
multthru(exp) exp の部分展開を行う◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-40.mx > tmp_lang/chunk-40.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-40.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-40.mx
display2d:false
distrib((a+b)*(c+d))
b*d+a*d+b*c+a*c
multthru((a+b)*(c+d))
(b+a)*d+(b+a)*c
distrib(1/((a+b)*(c+d)))
1/((b+a)*(d+c))
expand(1/((a+b)*(c+d)),1,0)
1/(b*d+a*d+b*c+a*c)
"/var/www/html/LANG/tmp_lang/chunk-40.mx"総和と積
product(exp,var,lo,hi) 総積関数
sum(exp,var,lo,hi) 総和関数◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-41.mx > tmp_lang/chunk-41.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-41.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-41.mx
display2d:false
product(f(x),x,2,5)
f(2)*f(3)*f(4)*f(5)
sum(x^k,k,0,n)
'sum(x^k,k,0,n)
simpsum:true
sum(x^k,k,0,n)
(x^(n+1)-1)/(x-1)
"/var/www/html/LANG/tmp_lang/chunk-41.mx"総和関数の簡約化
sumcontract(exp) 総和関数の簡約化を試みる
intosum(exp) 積の項を総和関数の中に入れる◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-42.mx > tmp_lang/chunk-42.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-42.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-42.mx
display2d:false
ex:sum(1/k^2,k,1,m)+sum(1/k^3,k,1,m)
'sum(1/k^2,k,1,m)+'sum(1/k^3,k,1,m)
sumcontract(ex)
'sum(1/k^2+1/k^3,k,1,m)
"/var/www/html/LANG/tmp_lang/chunk-42.mx"簡約化を行う関数
radcan(exp) 指数,対数,巾を含む式 exp の簡約化を試みる
scsimp(exp,rule_1,rule_2,...) 規則を考慮した簡約化を試みる\[\begin{eqnarray} && k^2\,n^2 + k^2\,m^2\,n^2 - k^2\,l^2\,n^2 - k^2\,l^2\,m^2\,n^2 \notag \\ && = k^2\,n^2\,(1+m^2-l^2-l^2\,m^2) = k^2\,n^2\,(1+m^2)\,(1-l^2) = k^4\,n^4 \notag \end{eqnarray}\]
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-43.mx > tmp_lang/chunk-43.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-43.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-43.mx
display2d:true
ex1:log(1+2*a^x+a^(2*x))/log(1+a^x)
radcan(ex1)
2
ex2:(log(x+x^2)-log(x))^a/log(1+x)^(a/2)
radcan(ex2)
a/2
log(x + 1)
/var/www/html/LANG/tmp_lang/chunk-43.mx\[ {\rm ex1:~~} \frac{\log (1+2a^x+a^{2x})}{\log (1+a^x)} = \frac{\log (1+a^x)^2}{\log (1+a^x)} = 2 \] \[ {\rm ex2:~~} \frac{ \left\{\log (x^2+x) - \log x \right\}^a}{\left\{\log (x+1)\right\}^{a/2}} = \frac{\left\{\log (x+1)\right\}^a}{\left\{\log (x+1)\right\}^{a/2}} = \left\{\log (x+1) \right\}^{a/2} \] 上記 ex2 では指数部の解釈に注意すること.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-44.mx > tmp_lang/chunk-44.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-44.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-44.mx
display2d:true
exp:(-k^2)*l^2*m^2*n^2-k^2*l^2*n^2+k^2*m^2*n^2+k^2*n^2
eq1:l^2+k^2 = 1
eq2:n^2-m^2 = 1
scsimp(exp,eq1,eq2)
4 4
k n
/var/www/html/LANG/tmp_lang/chunk-44.mx map() 各項毎に部分分数展開する
map(ratsimp,exp) 各項毎にratsimp()を作用する環境変数 factorag が false の場合, 有理式の整数部分の分解を抑制する. 環境変数 dontfactor に 変数リスト (デフォルト値は空) を設定し, その変数に対して因子分解を行わない様にしてもかまわない. dontfactor リストに含まれた変数よりも (CRE 表現に仮定された変数の順序を用いて) 小さな任意の変数に 対しても因子分解は実行されない.
環境変数 savefactors が true の場合, 式の因子を幾つかの同じ因子を含む式の因子分解の処理速度を 向上させるため, 関数で保存する.
環境変数 berlefact が false の場合, kronecker 因子分解アルゴリズムが使われ, そうでなければ, 標準の berlekamp アルゴリズムが使わる. intfaclim は大きな整数の引数分解を行うときに試みられる 最大の約数となる.false(この 場合は factor を明示的に呼び出した場合) に設定した場合, 整数が xnum(1 機械語長に適合する. なお, それ以外の数は bignum と呼ばれる)の場合には, 整数の因数分解を試みる. intfaclim の設定では, 内部に対しfactor の呼出に使われる. intfaclim を Maxima が大きな整数の因数分解に 長時間を費さない様に再設定してもかまわない.
環境変数 newfac が true の場合, 新しい因子分解ルーチンを用いる.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-45.mx > tmp_lang/chunk-45.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-45.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-45.mx
"/* 注1:次は,式の各項に無名関数を作用させる */"
map(lambda([u],partfrac(u,x)),x+1/(x^3+4*x^2+5*x+2))
1 1 1
----- - ----- + -------- + x
x + 2 x + 1 2
(x + 1)
"/* 注2:次は,式の各項に関数 ratsimp() を作用させる */"
map(ratsimp,x/(x^2+x)+(y^2+y)/y)
1
y + ----- + 1
x + 1
/var/www/html/LANG/tmp_lang/chunk-45.mx12.3 式に関する環境変数
● algebraic:false
true であれば,代数的整数の簡約化を行う. 代数的整数は最高次数の係数が 1
となる整数係数多項式の解と なる数のことである. これに対し,
代数的数もある. こちらは有理数係数多項式の解になる数のことである.
例えば, 純虚数 i や sqrt(2) の様な数は代数的整数になる. 又,
代数的整数と有理数は代数的数になる.
● berlefact:true
false であれば, kronecher の因子分解アルゴリズムが利用され, それ以外では
デフォルトの berlekamp アルゴリズムが使われる.
● dontfactor:[]
dontfactor に因子分解を行わない変数リストを設定する.
この変数リストを設定すると, CRE 形式を構成する上で 仮定された変数順序で,
ここで指定した変数よりも小さなものに対しても,
因子分解は実行されない.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-46.mx > tmp_lang/chunk-46.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-46.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-46.mx
exp:1/(a^2-1)-b^2/(a^2-1)
factor(exp)
(b - 1) (b + 1)
- ---------------
(a - 1) (a + 1)
ev(factor(exp),dontfactor:[a])
(b - 1) (b + 1)
- ---------------
2
a - 1
ev(factor(exp),dontfactor:[b])
2
b - 1
- ---------------
(a - 1) (a + 1)
ev(factor(exp),dontfactor:[a,b])
2
b - 1
- ------
2
a - 1
/var/www/html/LANG/tmp_lang/chunk-46.mx● exptisolate:false
true であれば, isolate(式, 変数) を実行する際に, 変数 に含まれる (%e
の様な) アトムの指数項についても 調べる.
● facexpand:true
factor で返された既約因子が展開された形式 (デフォルト) か, 再帰的
(通常の CRE) 形式であるかを制御する.
● factorag:false
false であれば有理式に含まれる整数の因数分解を抑制する.
● intfaclim:1000
大きな整数の因子分解を行うときに試す最大の約数. false を指定した場合
(利用者が factor を明示的に呼び出す 場合)や, 整数が xnum の場合 (つまり,
一つの機械語長に適合) に, 整数の完全な因数分解が試みられる. intfaclim
の設定は factor の内部呼び出しで用いられる. intfaclim
は大きな整数の因数分解に長時間を 費すのを防ぐために,
再設定してもかまわない.
● isolate_wrt_times:false
isolate 関数の動作に影響を与える. isolate_wrt_times が false であれば,
isolate 関数は 指定した変数を含まない項と含む項に分けて表示する. true
であれば, 更に式を分解し, 指定した変数を含む項も,
指定した積を除く項と指定した変数の項の積に 分解して表示する.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-47.mx > tmp_lang/chunk-47.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-47.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-47.mx
eq1:expand((a+b+x)^2)
2 2 2
x + 2 b x + 2 a x + b + 2 a b + a
isolate_wrt_times
false
exp1:expand((a+b+x)^2)
2 2 2
x + 2 b x + 2 a x + b + 2 a b + a
isolate_wrt_times
false
isolate(exp1,x)
2 2
b + 2 a b + a
2
x + 2 b x + 2 a x + %t6
isolate_wrt_times:true
true
isolate(exp1,x)
2 a
2 b
2
x + %t9 x + %t8 x + %t6
/var/www/html/LANG/tmp_lang/chunk-47.mx● keepfloat:false
true であれば, 浮動小数点を含む式が CRE 表現に変換される際に,
浮動小数点が有理数に近似変換されることを 防ぐ. なお,
浮動小数点が有理数に近似される誤差は ratepsilon で制御される.
● listconstvars:false
listofvars 関数の動作に影響を与える. true であれば,
定数として宣言した変数と MAXIMA の数学定数である %e, %pi, %i
が式に含まれていると, listofvars
はこれらの定数も変数として加えたリストを返す. false の場合,
数学定数と定数として宣言された変数は除外され, listvars
が返すリストには含まれない.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-48.mx > tmp_lang/chunk-48.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-48.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-48.mx
listofvars(x^2*y+aa+%e)
[aa, x, y]
listconstvars:true
listofvars(x^2*y+aa+%e)
[%e, aa, x, y]
/var/www/html/LANG/tmp_lang/chunk-48.mx● listdummyvars:true
false であれば, 式の疑似変数は listofvars
で返されるリストの中に含まれない. なお, 疑似変数は,sum 関数や product
関数等の添字や極限変数や定積分変数として利用される変数をいう.
● modulus:false
正素数 p が設定されていれば, 全ての有理関数での演算は p
の剰余で計算される (即ち, 多項 式環の係数体は zp となる). この場合, p/2
よりも大きな全ての整数のことは考えなくても良くなる. 例えば, p として 5
を 採った場合, 整数の剰余は {0,1,2,3,4} となるが, 3 = -2(mod 5), 4 =
-1(mod 5) となる (実際, 3-(-2) = 4-(-1) = 5(mod 5) となるので,
絶対値では {0,1,2} だけを考えれば良いことになる. そのため,
その分計算を簡単に行うことが可能になる. modulus
を再設定した時点で式が既に CRE 表現となって いると,
正しい結果を得るためには, 式に再び rat を作用させる必要がある. 即ち,
exp:rat(ratdisprep(exp)) を実行しなければならないことに注意する. なお,
modulus に素数でない正整数を 設定しようとすれば,
設定は実行されるものの警告が出力される. なお,
素数でない正整数を設定することはあまり 意味があることではない. 例えば,
modulus に 4 を設定すると \((2x + 1)(2x +
1)\) は 1 となり, \(x\) と \(x^2\) の項が消えてしまう.
● newfac:false
true であれば, factor は新しい因子分解ルーチンを用いる.
● optimprex:%
optimize 関数で生成された記号に使用される前置詞である.
● partswitch:false
true であれば, part 関数で選択した部分式が式中に存在しなければ end
が返される. false の場合は エラーメッセージが返される.
● ratalgdenom:true
true であれば, 分母の有理化を許容する. これを実行するためには, CRE
表現を利用しなければならない.
● ratdenomdivide:true
false であれば, ratexpand を作用させた式に対して,
分子の項を分離することを抑制する.
● ratepsilon:2.0e-8
有理数に変換する際に用いられる許容範囲.ratepsilon
よりも小さな浮動小数点
は無視される. 浮動小数点を有理数に変換したくなければ, keepfloat を
true
に設定する.
/home/inoue/bin/go tmp_lang/chunk-49.mx > tmp_lang/chunk-49.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-49.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-49.mx
ratepsilon
2.0E-15
ratsimp((1+2.0E-8)*x)
rat: replaced 1.00000002 by 50000000/49999999 = 1.00000002
50000000 x
----------
49999999
/var/www/html/LANG/tmp_lang/chunk-49.mxこの例で示す様に, ratsimp を作用させた場合に, ratepsilon よりも小さな 数が無視されて, 浮動小数点が有理数に変換されていることが判る.
● ratexpand:false
true であれば, それらが一般形式に変換されるか表示されたときに CRE 式が
展開される. false であれば, それらは再帰的な形式に置かれる.
● ratfac:false
true であれば, CRE 有理式に対して部分的に因子分解された形式で出力する.
有理的操作の間, factor パッケージを実際に呼ばずに,
式を可能な限り因子分解する. これでメモリ空間を節約し,
計算時間を幾らかを節約する. 有理式の分子と分母 は互いに素とする. 例えば,
rat((x^2 -1)4/(x+1)2) は (x-1)^4*(x+1)^2 となるが,
各部分の因子は互いに素とは限らない.
● ratprint:true
false であれば,
浮動小数点数から有理数への変換を報せるメッセージを出力しない. \
● ratsimpexpons:false
true であれば, 簡約化中に式の羃に対し, 自動的に ratsimp
が実行される.
● ratweights
ratweight 関数で設定される, 指定された重みのリストである. ratweights や
ratweight() でそのリストが表示される.
kill(…,ratweights) と save(…,ratweights); は両方共に動作する.
● ratwtlvl:false
ratweight 関数を用いた式をまとめる際の有理式 (CRE 表現)
の切捨ての制御で用いられる. なお, false であれば, 切捨ては生じない.
● resultant:subres
終結式の計算で用いるアルゴリズムを設定する. 殆どの問題では, subres が
最適である. 単変数の大きな次数や 2変数問題では, mod がより良い.
● savefactors:false
true であれば, 幾つかの同じ因子を含む後の式の展開の処理速度向上のため,
式の各因子がある関数で保存される.
12.4 式に関する関数
● args(exp)
式expが関数の場合は関数の引数を返す. 一般の式の場合, 内部表現で第 0 階層
を [で置換えたもの, 即ち, substpart(”[”, 式,0) と同じ 働きをする. なお,
この args と substpart の両方は inflag の設定に依存する.
● bezout(poly_1, poly_2, var)
多項式poly_1と多項式poly_2を変数varを主変数としたときの係数で構成される行列を返す.
行列の大きさは, 多項式 poly_1 と多項式 poly_2 の次数を各々 m, n
とすると, m+n 次の正方行列となる. この行列の determinant が 多項式
poly_1 と多項式 poly_2 の変数varによる終結式になる(章末参照).
この bezout 関数は determinant 関数と組合せると resultant
関数の代替になる.
● bothcoef(exp, var)
二成分のリストを返す. このリストの第一成分が式exp中の変数 var の係数
(式が CRE 表現であれば ratcoef, それ以外は coef で見つけたもの) となる.
第二成分が式の残りとなる.
即ち, [a, b] が返却値であれば, exp = a * var + b となる.
● coef(exp, var, order)
式expに含まれる\(var^{order}\)の項の係数を求める.
次数orderを省略すると 1 が設定される. 変数varはアトムか真の部分式である.
具体的には, x,sin(x),a[i+1],x+y 等である.
なお, 真の部分式の場合, (x+y)
が式の中に現れていなければならならない.
ここで, 変数の項を正確に求めるためには,
式の展開や因子分解が必要な場合もある. 何故なら, coef
関数では自動的に式の展開や因子分解が実行されれないからである.
/home/inoue/bin/go tmp_lang/chunk-50.mx > tmp_lang/chunk-50.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-50.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-50.mx
coeff(2*a*tan(x)+tan(x)+b = 5*tan(x)+3,tan(x))
2 a + 1 = 5
coeff(y+x*%e^x+1,x,0)
y + 1
/var/www/html/LANG/tmp_lang/chunk-50.mx● combine(exp)
式expに含まれる和の部分式を同じ分母でまとめて1つの項にする.
● content(poly, var)
二成分のリストを返す. このリストは,
変数varを多項式polyの主変数とした場合の各係数の
最大公約因子をリストの第一成分とし, 第二成分は第一成分で多項式を割った
もの (monic な多項式) となる.
/home/inoue/bin/go tmp_lang/chunk-51.mx > tmp_lang/chunk-51.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-51.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-51.mx
content(2*x*y+4*x^2*y^2,y)
2
[2 x, 2 x y + y]
/var/www/html/LANG/tmp_lang/chunk-51.mx\[ 4\,x^2\,y^2 + 2\,x\,y = 2\,x\,(2\,x\,y^2 + y) \quad としているだけ \]
● denom(rexp)
有理式rexpの分母 (DENOMinator) を返す. なお,
有理式が通常の多項式であれば, 1 が返される.
/home/inoue/bin/go tmp_lang/chunk-52.mx > tmp_lang/chunk-52.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-52.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-52.mx
denom((x^2+1)/(y^2+1))
2
y + 1
denom(x^2+1)
1
denom((1/2)*x^2+1/2)
1
/var/www/html/LANG/tmp_lang/chunk-52.mx● disolate(exp, var_1, … , var_n)
isolate(exp, var) に似ているが, こちらでは利用者が一つ以上の変数を同時
に孤立させることができる. 例えば, 重積分での変数変換や, 積分変数を二つか
それ以上を巻込んだ変数変換で便利である. この関数を利用するためには予め
load(disol) で読込む必要がある.
● dispform(exp)
● dispform(exp, all) 式expの外部表現を返す.MAXIMA
の式には表示される外部表現と内部処理で用いられる内 部表現がある.
dispform では返却される値は外部表現となるため, 外部表現 を扱う part
と組合せると便利である.
dispform(exp, all) で式全体を外部形式に変換する. この場合, 関数の引数と
して与えられた式も含めて処理が行われるため, part
関数の結果も異なることがある.
例えば, exp : cos(sqrt(x)) の場合, freeof(sqrt,exp) と
freeof(sqrt,dispform(exp)) は true となるが,
freeof(sqrt,dispform(exp,all)) は false となり, 関数の引数内部
の式に対しても freeof が使える様になる.
● divide(poly_1, poly_2, var_1, …, var_n)
多項式poly_2 による多項式poly_1の商と剰余を計算する. 各多項式は
変数var_nを主変数とし, その
他の変数は ratvars 関数に現れるものとする. 結果はリストで返却され,
第一成分が商, 第二成分が剰余となる.
/home/inoue/bin/go tmp_lang/chunk-53.mx > tmp_lang/chunk-53.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-53.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-53.mx
divide(x+y,x-y,x)
[1, 2 y]
divide(x+y,x-y)
[- 1, 2 x]
/var/www/html/LANG/tmp_lang/chunk-53.mx\[ \frac{x+y}{x-y} = \frac{(x-y)+2y}{x-y} = 1 + \frac{2y}{x-y} \] \[ \frac{x+y}{x-y} = - \frac{y+x}{y-x} = - \frac{(y-x)+2x}{y-x} = -1 + \frac{2x}{x-y} \]
● eliminate([eq_1, …, eq_n], [var_1, …,var_k])
方程式 (又は零と等しいと仮定した式) から続けて終結式を取ることで,
指定された変数の消去をおこなう. k 個の変数var_1,…,var_kが消去された n-k
個の式のリストを返す. 最初の変数1 は消去されて n-1 個の式を生成し, 変数2
以降も同様である. k=n の場合, 結果リストは k 個の 変数1, …, 変数k
を持たない一つの式となる. それから, solve
が最後の変数に対する終結式を解くために呼出される.
/home/inoue/bin/go tmp_lang/chunk-54.mx > tmp_lang/chunk-54.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-54.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-54.mx
exp1:2*x^2+y*x+z
exp2:3*x+5*y-z-1
exp3:z^2+x-y^2+5
eliminate([exp3,exp2,exp1],[y,z])
8 7 6 5 4 3 2
[7425 x - 1170 x + 1299 x + 12076 x + 22887 x - 5154 x - 1291 x
+ 7688 x + 15376]
eliminate([x+y = 2,2*x+3*y-5 = 0],[x,y])
[1]
eliminate([x+y = 2,2*x+3*y-5 = 0],[x])
[y - 1]
eliminate([x+y = 2,2*x+3*y+5 = 0],[x,y])
[- 9]
/var/www/html/LANG/tmp_lang/chunk-54.mx● ezgcd(poly_1, poly_2, …)
リストを返す. リストの成分は, 先ず第一成分が全ての多項式の GCD
(最大公約因子) とな
り, 残りの元が GCD で割った値になる. この ezgcd では ezgcd
アルゴリズムが常用されている.
● factcomb(exp)
式中に現われる階乗の係数を階乗それ自体で置換してまとめる. 例えば,
(n+1)*n! を (n+1)! にする. ここで, sumsplitfact:true が false
に設定されていれば, minfactorial が factcomb の後に適用される.
● factor(exp)
● factor(exp, p)
式expを整数上で既約因子に分解する. factor(exp, p) の場合, 最小多項式が p
となる整数体上で式の因子分解をおこなう. ただし,
環境変数の設定によって動作が異なる.
\[ \begin{eqnarray} && f = \sum_{i=0}^m \,a_i\, x^i = a_0 + a_1\,x + \cdots + a_m\,x^m = a_m\, \prod_{i=1}^m (x-\alpha_i) \notag \\ && g = \sum_{j=0}^n \,b_j\, x^j = b_0 + b_1\,x + \cdots + b_n\,x^n = b_n\, \prod_{j=1}^n (x-\beta_j) \notag \end{eqnarray} \]
● factorout(exp, var_1, var_2, …)
式 を f(var_1, var_2, …) * g の形式の項の和に書換える. ここで, g は
factorout の引数の各変数を含まない式の積で, f
は因子分解されたものになる.
● factorsum(exp)
グループ単位で 式 の因子分解を試みる.
このグループの項はそれらの和が因子分解可能なものである.
expand((x+y)2+(z+w)2) の結果は復元できるが,
expand((x+1)2+(x+y)2)
の結果は共通項が存在するために復元出来ない.
/home/inoue/bin/go tmp_lang/chunk-55.mx > tmp_lang/chunk-55.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-55.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-55.mx
ev(out:(x+1)*((u+v)^2+a*(w+z)^2),expand)
2 2 2 2 2 2
a x z + a z + 2 a w x z + 2 a w z + a w x + v x + 2 u v x + u x + a w
2 2
+ v + 2 u v + u
factorsum(out)
2 2
(x + 1) (a (z + w) + (v + u) )
/var/www/html/LANG/tmp_lang/chunk-55.mx● fasttimes(poly_1, poly_2)
多項式の積に対する特殊なアルゴリズムを用いて,
多項式poly_1と多項式poly_2の積 を計算する. これらの多項式は,
多変数で各次数に対して係数が 0 でない項が多く,
両者共に殆ど同じ大きされなければ効果があまりない.
n と m を多項式の次数とすると, 古典的な積では n*m
のオーダーで計算を行うが, fasttimes を用いると max(n,m)**1.585
のオーダーとなる.
● freeof(x_1, … , x_n, exp) x_i が式expの中に現われなければ, true を返し, それ以外は false を返す. x_i はアトム, 添字付けられた名前, 関数, 或いは二重引用符””で括られた演算子となる. なお, 関数内部で利用される疑似変数をx_iに指定した場合, その疑似変数が式expに含まれていても true を返す.
● fullratsimp(exp)
fullratsimp は非有理的簡約化に続けて ratsimp
を式に変化が生じなくなる迄適用する. 例えば, 式
exp:(x(a/2)+1)2*(x(a/2)-1)2/(x^a-1)
に対しては,
ratsimp(exp) により (x(2a)-2xa+1)/(x^a-1) を返し,
fullratsimp(exp) では x^a-1 を返す.
● fullratsimp(exp, var_1, …, var_n)
ratsimp と rat と同様に一つ又はそれ以上の引数を取る.
● gcd(exp_1, exp_2, var_1,…)
式exp_1と式exp_2の最大公約数を計算する. 環境変数 gcd
で適用されるアルゴリズムを決める. 環境変数 gcd に ez, eez, subres, red
や spmod を設定できる.
gcd:false であれば, gcd(exp_1, exp_2, var_1) は全ての変数に対して常に 1
を返す. 多くの関数 (例えば, ratsimp, factor, 等) は gcd
を裏側で計算している.
同次多項式に対しては, gcd:subres を用いることを推奨する.
代数的整数の場合, 例えば,
gcd(x^2-2sqrt(2)x+2,x-sqrt(2))
の gcd を計算するためには algebraic が true でなければならず, gcd が ez
であってはならない.
subres は新しいアルゴリズムで red 設定を用いている場合, それを subres
に変更すべきである なお, 環境変数 gcd が false であれば, 式が CRE
表現に変換すると, 最大公約因子を取らない様になる. これは gcd
が必要とされない場合には計算の高速化に繋がることがある.
● gcdex(poly_1, poly_2, var)
● gcdex(poly_1, poly_2)
3 個の多項式を成分とするリスト [a,b,c] を返す. この多項式 c は引数の
多項式poly_1と多項式poly_2の最大公約因子 (gcd) で, 多項式 a, b は
c = a * poly_1 + b * poly_2 を満す.
ここでのアルゴリズムはユークリッドの互除法に基く. なお,
多項式が単変数の場合は変数varを 指定する必要はないが, 多変数の場合,
多項式を変数var で指定した単変数の多項式と看倣して gcd を計算する.
/home/inoue/bin/go tmp_lang/chunk-56.mx > tmp_lang/chunk-56.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-56.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-56.mx
gcdex(x^2+1,x^3+4)
2
x + 4 x - 1 x + 4
/R/ [- ------------, -----, 1]
17 17
gcdex(x*(y+1),y^2-1,x)
1
/R/ [0, ------, 1]
2
y - 1
gcdex(x*(y+1),y^2-1,y)
/R/ [1, 0, x y + x]
/var/www/html/LANG/tmp_lang/chunk-56.mx\[
1 = - \frac{x^2+4x-1}{7}\times (1+x^2) + \frac{x+4}{17}\times (4+x^3)
\] \[
1 = 0 \times x(1+y) + \frac{1}{y^2-1} \times (y^2-1)
\] \[
xy+x = 1 \times x(1+y) + 0 \times (y^2-1)
\] ここで, 最後の多変数の例で, gcdex(x(y+1),y^2-1,x)
の結果で, gcd として 1 を返していることに注意する. この場合, 多項式環
k(y)[x] で処理を行っているので, 共通の因子として期待さ れる y+1
にはならない. ここで, k(y)[x] は x を主変数とした x と y の多項式環,
つまり, x の多項式で, その係数が k 上の y の多項式となるものとして, x と
y の k[x,y] 多項式を見直したためである. 一般的に可換環 k が ufd であ
れば, k[x] も ufd になることが知られている. そのため, ユークリッド
の互除法が利用可能になるので, gcdex は必ず結果を返す.
gcdex(x(y+1),y 2-1,y); とすれば, 多項式環 k(x)[y] の話に
なるので 1 ではなく, xy+x
になる. ただし, この返却値が良いものとは言い難いものがある.
● gcfactor(Gauss_integer)
Gauss 整数上で Gauss 整数Gauss_integerの因子分解をおこなう. なお, Gauss
整数とは, 複素数 a + bi で, a と b が整数になる. 因子は a と b
を非負とすることで正規化されている.
/home/inoue/bin/go tmp_lang/chunk-57.mx > tmp_lang/chunk-57.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-57.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-57.mx
gcfactor(5*%i+1)
(1 + %i) (3 + 2 %i)
gcfactor(2)
2
- %i (1 + %i)
/var/www/html/LANG/tmp_lang/chunk-57.mx\[ (1+i)(3+i) = 3 + (3+2)i +(-2) = 1 + 5i \] \[ -i(1+i)^2 = -i(1+2i-1) = 2 \]
● gfactor(poly)
Gauss 整数上で多項式polyの因子分解を行なう. これは factor(exp,a^2+1)
と同様の結果を返す.
/home/inoue/bin/go tmp_lang/chunk-58.mx > tmp_lang/chunk-58.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-58.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-58.mx
gfactor(x^4-1)
(x - 1) (x + 1) (x - %i) (x + %i)
factor(x^4-1,a^2+1)
(x - 1) (x + 1) (x - a) (x + a)
/var/www/html/LANG/tmp_lang/chunk-58.mxこの例で, factor を用いたものでは方程式 \(x^2 + 1 = 0\) の解となる 代数的整数 a(= i) を用いて x^4-1 を因子分解している.
● gfactorsum(poly)
factorsum に似ているが, factor の代りに gfactor が適用される.
/home/inoue/bin/go tmp_lang/chunk-59.mx > tmp_lang/chunk-59.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-59.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-59.mx
gfactorsum(x^2+1)
(x - %i) (x + %i)
factor(x^2+1)
2
x + 1
/var/www/html/LANG/tmp_lang/chunk-59.mx\[ (x-i)(x+i) = x^2 -(-1) = x^2 + 1 \]
● hipow(poly, var)
多項式polyに含まれる変数varの項の最高次数を返す. なお, hipow
では式の展開を 自分で実行しないため, 予め式を展開しておく必要がある.
以下の例では (x + 1)^4 を展開せずに hipow を用いた結果と expand
で展開した式 に対して hipow を用いた結果を示している.
/home/inoue/bin/go tmp_lang/chunk-60.mx > tmp_lang/chunk-60.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-60.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-60.mx
hipow((x+1)^4,x)
1
hipow(expand((x+1)^4),x)
4
/var/www/html/LANG/tmp_lang/chunk-60.mxなお, hipow の逆の低い次数を検出する関数は lopow である.
● indices(exp)
二つの元のリストを返す. 最初のものは式expで利用されていない添数のリスト
(これらは一 度だけ現われる) で, 二番目のものは式expの無効添数のリスト
(これらは丁度二度現れる) となる.
● inpart(exp, p_1, … , p_k) part と似ているが, part が MAXIMA に表示された式expに対して作用するが, inpart の場合は式expの内部表現に対して直接作用する. 内部表現に直接作用 するので, その分, 処理が速くなる. 和や積, 単一演算子 (unary) としての 演算子, 差と商を扱う場合, 部分式の順序に注意を払う必要がある.
● isolate(exp, var)
isolate
は式expから変数varとの積を持つ部分式と持たない部分式に分けて表示する.
変数var を持たない部分式は中間ラベルで置換えられ,
式全体は中間ラベルと変数varの 項の和で表現される. なお,
isolate_wrt_times が false の場合,
式expは変数varとの積を持たない部分式と
変数varとの積を持つ部分式に分解して表示する.
isolate_wrt_times が true の場合, isolate は更に式expを分解し,
項も変数varの羃とそれ以外の変数との積に分解して表示する. なお, isolate
は式の展開を行わない.
/home/inoue/bin/go tmp_lang/chunk-61.mx > tmp_lang/chunk-61.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-61.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-61.mx
isolate_wrt_times:false
false
exp1:expand((1+a+x)^2)
2 2
x + 2 a x + 2 x + a + 2 a + 1
isolate(exp1,x)
2
a + 2 a + 1
2
x + 2 a x + 2 x + %t4
isolate_wrt_times:true
true
isolate(exp1,x)
2 a
2
x + %t6 x + 2 x + %t4
isolate((1+a+x)^2,x)
a + 1
2
(x + %t7)
/var/www/html/LANG/tmp_lang/chunk-61.mx● listofvars(exp)
式 exp の変数リストを生成する. 環境変数 listconstvars が true であれば,
式 exp に MAXIMA の数学定数 %e, %pi, %i や定数として宣言した変数も
listofvars が返すリストに含められる. ただし, デフォルトの false の場合,
定数を除外したリストを返す.
● lopow(poly, var)
多項式polyの変数varの次数で,
明示的に現われものの中で最も低い次数を返す.
● mod(poly)
● mod(poly, k)
多項式polyを環境変数 modulus で指定した値に対する剰余を計算する. なお,
環境変数 modulus は デフォルトでは false のため, mod(poly)
を実行するとエラーになる. 環境変数 modulus の値と無関係に,
多項式の剰余を計算したければ, mod(poly,
k)で多項式polyの整数kによる剰余を計算する. なお, 環境変数 modulus
の値は変更されない.
● multthru(exp)
● multthru(exp_1, exp_2)
multthru(exp) で式expの部分展開をおこなう. つまり, 式 が \(f1 * f2 * \cdots * fn\) の形式で,
各因子の中で, 羃乗でない 式 中で最も左側の因子を fi とすると, 式 の fi
以外の因子と fi の 項との積の和に分解する. 例えば, \((x+1)^2*(z+1)*(y+1)\) の場合,
最も左側の因子 \(z+1\) で式が展開され,
\((x+1)^2*(y+1)*z+(x+1)^2*(y+1)\)
となる.
multthru(exp_1, exp_2) の場合, exp_2の各項をexp_1倍にする. つまり,
multthru(exp_1 * exp_2) と同値である. なお, exp_2
には方程式を指定できる. この場合, 演算子=の二つの被演算子に 式1
との積が返される. なお, multthru は羃乗された和の展開は行わない.
この関数は和に対する可換, 或いは非可換積の分配に関して最も速い.
/home/inoue/bin/go tmp_lang/chunk-62.mx > tmp_lang/chunk-62.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-62.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-62.mx
multthru((x+1)^2*(z+1)*(y+1))
2 2
(x + 1) (y + 1) z + (x + 1) (y + 1)
multthru((x+1)^2*(y+1)^2*(z+1)^2,z+1)
2 2 2 2 2 2
(x + 1) (y + 1) z (z + 1) + (x + 1) (y + 1) (z + 1)
multthru((x+1)^2*(y+1)^2*(z+1)^2,x+1)
2 2 2 2 2 2
x (x + 1) (y + 1) (z + 1) + (x + 1) (y + 1) (z + 1)
multthru((x+1)^2*(y+1)^2*(z+1)^2,x^2+1 = 0)
2 2 2 2 2 2 2
x (x + 1) (y + 1) (z + 1) + (x + 1) (y + 1) (z + 1) = 0
/var/www/html/LANG/tmp_lang/chunk-62.mx● nterms(exp) 式expを展開したときの項数を返す. ただし, 関数の引数に関しては, 展開されず, ただ一つの項として数えられる.
/home/inoue/bin/go tmp_lang/chunk-63.mx > tmp_lang/chunk-63.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-63.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-63.mx
nterms((x+1)^2)
3
nterms(sin(x+1)^2)
1
nterms((sin(x+1)+1)^3)
4
nterms((sin((x+1)^10)+1)^3)
4
/var/www/html/LANG/tmp_lang/chunk-63.mx● num(rexp)
有理式rexpの分子(NUMerator) を返す.
● optimize(exp)
式expに含まれる共通部分式を内部変数で置換し, 効率的に
計算出来る様な式に変換し,その変換式を返す.この際に, block
文が用いられる. ただし, 共通部分式が無い場合は, 式をそのまま返す.
/home/inoue/bin/go tmp_lang/chunk-64.mx > tmp_lang/chunk-64.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-64.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-64.mx
display2d:false
optimize((x+1)^3+1/(x+1)^2+exp((x+1)^2))
block([%1,%2],%1:x+1,%2:%1^2,%e^%2+%1^3+1/%2)
ans1:solve(x^4+x^3+3*x-1 = 0,x)
[x = (-sqrt(5^(3/2)/2-1/2)/2)-sqrt(5)/4+(-1)/4,
x = sqrt(5^(3/2)/2-1/2)/2-sqrt(5)/4+(-1)/4,
x = (-sqrt((-5^(3/2)/2)-1/2)/2)+sqrt(5)/4+(-1)/4,
x = sqrt((-5^(3/2)/2)-1/2)/2+sqrt(5)/4+(-1)/4]
optimize(ans1)
block([%1,%2,%3,%4,%5,%6],%1:sqrt(5),%2:((-1)*%1)/4,%3:%1^3,%4:sqrt(%3/2-1/2),
%5:%1/4,%6:sqrt((-%3/2)-1/2),
[x = (-%4/2)+%2+(-1)/4,x = %4/2+%2+(-1)/4,x = (-%6/2)+%5+(-1)/4,
x = %6/2+%5+(-1)/4])
"/var/www/html/LANG/tmp_lang/chunk-64.mx"● part(exp, n_1, …, n_k)
式expの部分式を抽出する. 抽出する部分式はn_1,…, n_k で指定する. この
part 関数は 表示式(外部表現)から部分式を取出すもので, 内部表現か
ら部分式を取出す関数は inpart になる.
部分式の取出し方は, 最初に式から n_1 番目のパートを取り出す. 次に,取
出したパートから n_2 番目のサブパートを取り出す. 以降同様に n_(k-1) 番目
のパートから n_k 番目のサブパートを取り出し,
このサブパートを結果として返す.
/home/inoue/bin/go tmp_lang/chunk-65.mx > tmp_lang/chunk-65.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-65.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-65.mx
part((x+1)^3+2,1)
3
(x + 1)
part((x+1)^3+2,1,1)
x + 1
part((x+1)^3+2,1,1,1)
x
part(x+y+z,[1,3])
z + x
/var/www/html/LANG/tmp_lang/chunk-65.mx部分式の取出し方を見て判る様に,
式を階層構造をもつリストと見なしている. そのため, part は MAXIMA
のリストや行列でも, その成分の取出しに使える.
part 関数の最後の引数が添字のリストであれば, 幾つかのパートが取り出され,
各々がそのリストの添数に関連したものとなる. 例えば, part(x+y+z,[1,3]) は
z+x となる. 環境変数 piece には part
関数を用いて取出した最新のパートが保存される. 環境変数 partswitch が
true の場合, 式に指定した成分が存在しないときに end を返す. false
の場合は, エラーメッセージを返す.
● partition(exp, var) 与えられた式expを分解し, 二つのパートを要素とするリストを返す. これらの部分式は式 exp の第一層に 属するもので, 第一成分が変数varを含まない部分式, 第二成分が変数varを含む部分式となる.
/home/inoue/bin/go tmp_lang/chunk-66.mx > tmp_lang/chunk-66.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-66.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-66.mx
part(x+1,0)
+
partition(x+1,x)
[1, x]
part((x+1)*y,0)
*
partition((x+1)*y,x)
[y, x + 1]
part([x+1,y],0)
[
partition([x+1,y],x)
[[y], [x + 1]]
/var/www/html/LANG/tmp_lang/chunk-66.mx● pickapart(exp, k)
整数kで指定された式expの階層に含まれる全てのパートを %t ラベルに割当て,
ラベルを用いた式に式を変換する. 階層指定は part 関数と同様で,
表示された形式に対して指定する. pickapart 関数は大きな式を扱う際に, part
関数を使わずに部分式に変数を自動的に割当てることにも使える.
/home/inoue/bin/go tmp_lang/chunk-67.mx > tmp_lang/chunk-67.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-67.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-67.mx
exp:(x+1)^3
pickapart(exp,1)
x + 1
3
%t3
exp2:expand((x+1)^3)
3 2
x + 3 x + 3 x + 1
pickapart(exp2,1)
3
x
2
3 x
3 x
%t7 + %t6 + %t5 + 1
/var/www/html/LANG/tmp_lang/chunk-67.mx● piece()
part 関数を用いたときに選ばれた最後の式を保つ. 関数の実行中に設定されて,
その関数自身の中で参照することができる.
● powers(exp, var)
式expに現われる 変数varの次数リストを返す. 利用前に予め load(powers)
で読込を行う必要がある.
● product(exp, ind, low, high)
添字変数indの下限lowから上限high迄の式expの値の積を与える. 評価は sum
関数と似ている. 積の簡約化はこの時点では使えない.
上限が下限より小になると空の積となるが, この場合, product
はエラー出力ではなく 1 を返す.
● quotient(poly_1, poly_2, var_1, … )
多項式poly_2による多項式poly_1の割り算の商を計算する.
● rat(exp, var_1, … , var_n)
式expを CRE 表現に展開して変換を行い, 全ての項を共通の分母でまとめて,
浮動小数点を許容範囲 ratepsilon[2.0e-8] 以内で有理数に変換し,
分子と分母の最大公約因子を除去する.
指定されていれば, 変数は ratvars にて var_1, …, var_n の順で順序付ける.
rat は +, -, *, /と羃乗の他の関数を一般的には簡易化しない. この rat には
ratfac, ratprint, keepfloat
といった直接動作に関連する環境変数がある.
/home/inoue/bin/go tmp_lang/chunk-68.mx > tmp_lang/chunk-68.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-68.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-68.mx
c0:(x-2*y)^4/(x^2-4*y^2)^2+1
rat(c0,y,x)
2 2
2 x + 8 y
/R/ -----------------
2 2
x + 4 y x + 4 y
c1:(((x-2*y)^4/(x^2-4*y^2)^2+1)*(y+a)*(2*y+x))/(4*y^2+x^2)
rat(c1,y,a,x)
2 a + 2 y
/R/ ---------
x + 2 y
/var/www/html/LANG/tmp_lang/chunk-68.mx\[ \frac{\left(1 + \frac{(x-2y)^4}{(x^2-4y^2)^2}\right)\,(y+a)(2y+x)}{x^2 + 4y^2} = \frac{2(x^2+4y^2)}{(x+2y)^2} \times \frac{(y+a)(2y+x)}{x^2 + 4y^2} = \frac{2(y+a)}{x+2y} \]
● ratcoef(exp_1, exp_2, n)
● ratcoef(exp_1, exp_2)
式exp_1の \((exp_2)^n\) の係数を返す. n
が 1 の場合は n が省略できる. なお, 返却値には, 式exp_2
に含まれる変数を関数の変数としても含まない.
この様な係数が存在しない場合は零を返す. ratcoef
は展開等を行って式を簡約化するので, 単純に \((exp_2)^n\) の係数を返す coef
と異った答を返す.
例えば, ratcoef((x+1)/y+x,x) は (y+1)/y を返却するが, coef は 1
を返す.
ratcoef(exp_1, exp_2, 0) は, 式exp_1から式exp_2を含まない項の和を返す.
そのため, 式exp_2が負の羃の項に含まれれば, ratcoef
は使ってはいけない.
式exp_1が有理的に簡約化されていれば,
係数は予期した様に現れないかもしれない.
/home/inoue/bin/go tmp_lang/chunk-69.mx > tmp_lang/chunk-69.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-69.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-69.mx
ratcoef((x+1)/y+x,x)
y + 1
-----
y
coef((x+1)/y+x,x)
x + 1
coef(----- + x, x)
y
s:a*x+b*x+5
ratcoef(s,x)
b + a
ratcoef(s,a+b)
x
/var/www/html/LANG/tmp_lang/chunk-69.mx● ratdenom(rexp)
有理式rexpの分母を計算する.有理式が一般形式で,
一般式の結果を必要とするのであれば, dem 関数を用いるべきである.
● ratdiff(rexp, var)
有理式rexpを変数varに対して微分する. 有理式に対しては diff
よりも処理が速く,
計算結果は CRE 表現になる.
なお, ratdiff は因子分解された CRE 表現には使ってはいけない.
因子分解された式では diff を使おう.
/home/inoue/bin/go tmp_lang/chunk-70.mx > tmp_lang/chunk-70.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-70.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-70.mx
d1:(4*x^3+10*x-11)/(x^5+5)
ratdiff(d1,x)
7 5 4 2
8 x + 40 x - 55 x - 60 x - 50
- ---------------------------------
10 5
x + 10 x + 25
/var/www/html/LANG/tmp_lang/chunk-70.mx● ratdisrep(exp)
式expを CRE表現から一般形式に変換する. 伝染を止めたり, 非有理的な文脈
(context) の中で 有理関数を利用する場合, これは時々便利である. 殆どの
CRE 関数は CRE と非 CRE 式に対して作用するが,
答は異った形式を取る.
与えられた式が非 CRE 表現であれば, 与式をを変更しないで返す.
● ratexpand(exp)
和の積や指数の和を掛け, 共通の分子で因子をまとめ,
分子と分母の共通約数を通分し, 分子を分母
によって割られた項へと分割して式expの展開を行う. これは式expを CRE
表現に変換し, それからを一般形式に戻して達成している.
ratexpand に影響を与える環境変数には ratexpand, ratdenomdivide, keepoat
がある.
/home/inoue/bin/go tmp_lang/chunk-71.mx > tmp_lang/chunk-71.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-71.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-71.mx
ex1:ratexpand((2*x-3*y)^3)
3 2 2 3
(- 27 y ) + 54 x y - 36 x y + 8 x
ex2:(x-1)/(x+1)^2+1/(x-1)
expand(ex2)
x 1 1
------------ - ------------ + -----
2 2 x - 1
x + 2 x + 1 x + 2 x + 1
ratexpand(ex2)
2
2 x 2
--------------- + ---------------
3 2 3 2
x + x - x - 1 x + x - x - 1
/var/www/html/LANG/tmp_lang/chunk-71.mx\[ \frac{x-1}{(x+1)^2}+\frac{1}{x-1} = \frac{(x-1)^2 + (x+1)^2}{(x+1)^2\,(x-1)} = \frac{2x^2+2}{(x+1)^2\,(x-1)} \]
● ratnumer(rexp)
有理式expの分子を CRE 表現で返す. 一般形式の有理式に対して, CRE
表現の結果が不要であれば, num 関数を用いる.
● ratnump(exp)
式expが有理数式であれば true, それ以外は false を返す.
● ratp(exp)
式expが CRE か拡張 CRE 表現であれば true, それ以外は false となる.
● ratsimp(exp)
● ratsimp(exp, var_1, … , var_n)
非有理的関数に対して, 有理的に式expとその部分式の全てを引数も含めて
(ratexpand の様に) 簡易化する. 結果は二つの多項式の商として,
再帰的な形式で返される. 即ち,
主変数の係数は他の変数の多項式となっており,
その係数もまた変数の順序に沿って,
主変数の次に順序の高い変数の多項式の係数とまとめられている. 変数は
ratexpand の様に非有理的関数 (例えば, sin(x**2+1) を含むが, ratsimp
で非有理的関数に対する引数は有理的に簡約化される. ratsimp は ratexpand
に影響を与える幾つかの環境変数の影響を受けることに注意する.
なお, ratsimp(exp, var_1,…, var_n) で, ratvars に変数の var_1,…
を設定した場合と同様に,
この変数の並びの順序で有理的簡約化をおこなう.
/home/inoue/bin/go tmp_lang/chunk-72.mx > tmp_lang/chunk-72.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-72.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-72.mx
ex1:sin(x/(x^2+x)) = %e^((log(x)+1)^2-log(x)^2)
ratsimp(ex1)
1 2
sin(-----) = %e x
x + 1
ex2:((x-1)^(3/2)-(x+1)*sqrt(x-1))/sqrt((x-1)*(x+1))
ratsimp(ex2)
2 sqrt(x - 1)
- -------------
2
sqrt(x - 1)
ev(x^(a+1/a),ratsimpexpons:true)
2
a + 1
------
a
x
/var/www/html/LANG/tmp_lang/chunk-72.mx\[{\rm ex1:~~} \left\{1 + \log x \right\}^2 - (\log x)^2 = 2\log x + 1 \] \[ \qquad t = e^{2\log x + 1}, \quad \log t = 2 \log x + 1 = \log x^2 + \log e = \log (e \cdot x^2) \]
● ratvars(var_1, … , var_n)
n 個の変数の引数でリストを構成する. ratvars を実行した後,
リスト中の一番右側の 変数 var_n が有理式にあれば,
それを有理式の主変数とする. 又,
他の変数の順序はリストの右から左への順番に従う. ある変数が ratvars
リストから抜けていれば, その変数は一番左側の 変数1
よりも低い順序が付けらる.
ratvars の引数は変数, 或いは非有理的関数 (sin(x) の様な関数)
のいずれかでなければならない. なお, 環境変数 ratvars は,
この関数に与えられた引数のリストとなる.
/home/inoue/bin/go tmp_lang/chunk-73.mx > tmp_lang/chunk-73.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-73.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-73.mx
ratvars(x,y,z)
[x, y, z]
rat(x+y+z)
/R/ z + y + x
rat(a+x+y+z)
/R/ z + y + x + a
ratvars(z,y,x)
[z, y, x]
rat(a+x+y+z)
/R/ x + y + z + a
/var/www/html/LANG/tmp_lang/chunk-73.mx● ratweight(var_1, w_1, … , var_n, w_n)
重みw_iを変数var_iに割当てる. その重みが環境変数 raywtlvl の値
[デフォルト値は false で, 切捨てなしを意味する] を超過したときに, 項が 0
で置き換えられる. 項の重みは項の中の変数の羃を重みに掛けた積の和となる.
例えば,
3*v1**2v2 の重みは 2w1+w2 となる. この切捨ては, 式の CRE
表現の積や羃乗を実行するときのみに生じる. なお, ratfac と ratweight
の手法は互換性がないので, 両方同時に使えない.
/home/inoue/bin/go tmp_lang/chunk-74.mx > tmp_lang/chunk-74.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-74.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-74.mx
ratweight(a,1,b,1)
[a, 1, b, 1]
exp1:rat(a+b+1)
exp1^2
2 2
/R/ b + (2 a + 2) b + a + 2 a + 1
ratwtlvl:1
exp1^2
/R/ 2 b + 2 a + 1
/var/www/html/LANG/tmp_lang/chunk-74.mx● rectform(exp)
式expをa+b%i の形式で返す. 式expが複素数の場合, a と b
は実数となるが, そうでない場合には, %i を持たない部分と%i
で括られた式に分解し, 内部の項順序に従って出力されるため, 正確に
a+b%i の形式にはならない.
/home/inoue/bin/go tmp_lang/chunk-75.mx > tmp_lang/chunk-75.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-75.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-75.mx
rectform((x+%i)^2)
2
x + 2 %i x - 1
rectform((10+%i)^2)
20 %i + 99
/var/www/html/LANG/tmp_lang/chunk-75.mx● remainder(poly_1, poly_2, var_1, … )
多項式poly_2による 多項式poly_1の割算による剰余を計算する.
● remvalue(var_1, var_2, …)
● remvalue(all)
指定した利用者変数var_1,var_2,…の値をシステムから削除する. ここで,
利用者変数は添字付きでも構わない. remvalue(all) で,
全ての利用者変数が削除される.
● resultant(poly_1, poly_2, var)
多項式poly_1と多項式poly_2の終結式(章末参照)を計算し,
指定した変数varを消去する. なお,
終結式は多項式poly_1と多項式poly_2が共通の定数の因子を持つ場合に限って零になる多項式である.
多項式poly_1と多項式poly_2を変数varの多項式と看倣した場合の係数から構成される行列の行列式から計算できる.
なお, 多項式poly_1, 多項式poly_2が因子分解可能であれば resultant
を呼び出す前に factor を呼び出すと良い.
● showratvars(exp)
式expの ratvars(CRE 変数) のリストを返す.
/home/inoue/bin/go tmp_lang/chunk-76.mx > tmp_lang/chunk-76.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-76.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-76.mx
exp:x^2+y^2+z^3
3 2 2
z + y + x
showratvars(exp)
[x, y, z]
/var/www/html/LANG/tmp_lang/chunk-76.mx● sqfr(exp)
factor と似ているが, 多項式因子は無平方 (square-free) となる. Maxima の
sqfr は与えられた式に対し, この無平方分解を計算する.
無平方分解 sqfr と因子分解 factor との違いを
\(4 x^4 + 4 x^3 - 3 x^2 - 4 x - 1\)
で比較する.
/home/inoue/bin/go tmp_lang/chunk-77.mx > tmp_lang/chunk-77.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-77.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-77.mx
sqfr(4*x^4+4*x^3+(-3)*x^2+(-4)*x-1)
2 2
(2 x + 1) (x - 1)
factor(4*x^4+4*x^3+(-3)*x^2+(-4)*x-1)
2
(x - 1) (x + 1) (2 x + 1)
/var/www/html/LANG/tmp_lang/chunk-77.mxこの例で示す様に, factor は式を徹底して分解しているのに対し, sqfr
は程々で止めている. この様に,
無平方因子分解は通常の因子分解程の手間をかけない. 更に,
有理多項式の積分計算では, 無平方な因子に分母を分解して,
各因子を分母に持つ式に変形して積分を行うアルゴリズムもある.
この無平方分解は幅広く利用されている.
● sum(exp, ind, low, high)
添字変数indを下限lowから上限high迄の値の式expの和を取る.
上限highと下限lowが整数で異なっていれば,
和の各々の項は評価されて互いに加えられる. simpsum が true の場合,
その結果も簡約化される. 簡約化は閉形式の生成が出来る場合がある. simpsum
が false, 或いは, ’sum が用いられた場合, 値は sum の名詞型で, 数学の Σ
表記で表示される.
なお, 上限highが下限lowよりも小さい場合には, ”空の総和 (empty sum)”
になり, sum はエラー出力ではなく 0 を返す. sum は微分, 和, 差や積が
可能で, それらの自動的簡約化も行われる.
cauchysum が true であれば, 和同士の掛け算で通常の積ではなく Cauchy 積
が利用される. Cauchy 積では内部和の添字が独立に変化するのではなく,
外部添数の関数となる. 環境変数の simpsum はデフォルトで false
が設定されている. 以下に simpsum の値による違いを示す.
/home/inoue/bin/go tmp_lang/chunk-78.mx > tmp_lang/chunk-78.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-78.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-78.mx
simpsum
false
sum(x^n,n,0,m)
m
====
\ n
> x
/
====
n = 0
simpsum:true
true
sum(x^n,n,0,m)
m + 1
x - 1
----------
x - 1
/var/www/html/LANG/tmp_lang/chunk-78.mxこの様に simpsum が false の場合, sum(x,n,0,m) の簡約化は実行されないが, simpsum が true の場合には, 自動的に簡約化が実行される. 又, sum(x,n,0,inf) とすると, x の絶対値から 1 を引いたものが 正か負か零であるかを利用者が指定することで簡約化が行える.
● totaldisrep(exp)
CRE 表現から一般形式へ式expの全ての部分式を変換する. 式expが CRE
表現であれば, ratdisrep と同じことになるが, そうでなければ, totaldisprep
がそれを ”totally disrep” すれば, ratdisrep
は式expを変更せずに返すことはない. これは ratdisprep を実行している式,
例えば, 方程式, リスト, 行列等で 幾つかの CRE
表現の部分式を持つものに便利である.
終結式
%終結式(p.244) 多項式 \(f\),\(g\) の解をそれぞれ,\(\alpha_i~~(i=1,2,\cdots,m)\), \(\beta_j~~(j=1,2,\cdots,n)\) とする. \[\begin{eqnarray} {\rm res}(f,\,g,\,x) &=& a_m^n\,b_n^m\, \prod_{1 \leq i \leq m, 1 \leq j \leq n}\,(\alpha_i - \beta_j) \notag \\ &=& \left|\matrix{ a_m & a_{m-1} & \cdots & \cdots & a_1 & a_0 & \cdots & 0 \cr \vdots & \ddots & \ddots & & & \ddots & \ddots & \vdots \cr 0 & \cdots & a_m & a_{m-1} & \cdots & \cdots & a_1 & a_0 \cr b_n & b_{n-1} & \cdots & \cdots & b_1 & b_0 & \cdots & 0 \cr \vdots & \ddots & \ddots & & & \ddots & \ddots & \vdots \cr 0 & \cdots & b_n & b_{n-1} & \cdots & \cdots & b_1 & b_0 } \right| \notag \end{eqnarray}\] \[\begin{eqnarray} && f = a_0 + a_1\,x + a_2\,x^2 \notag \\ && g = b_0 + b_1\,x \notag \end{eqnarray}\] 上記終結式の第1表現より,2つの多項式が共通因子をもつとき,終結式の 値は 0 となる.また,第2表現を用いて,多項式の因子分解を行うことなく共 通因子の有無を判定することが出来る.以下に例を示す.\ 例1.終結式の計算例 \[\begin{eqnarray} {\rm res}(f,\,g,\,x) &=& \left|\matrix{ a_2 & a_1 & a_0 \cr b_1 & b_0 & 0 \cr 0 & b_1 & b_0 \cr } \right| = \frac{1}{a_0\,b_0}\,\left|\matrix{ a_2\,b_0 & a_1\,b_0 & a_0\,b_0 \cr b_1 & b_0 & 0 \cr 0 & a_0\,b_1 & a_0\,b_0 \cr } \right| \notag \\ &=& \frac{1}{a_0\,b_0}\,\left|\matrix{ a_2\,b_0 & a_1\,b_0 - a_0\,b_1 & 0 \cr b_1 & b_0 & 0 \cr 0 & a_0\,b_1 & a_0\,b_0 \cr } \right| = \left|\matrix{ a_2\,b_0 & a_1\,b_0 - a_0\,b_1 \cr b_1 & b_0 \cr } \right| \notag \\ &=& a_2\,b_0^2 - (a_1\,b_0 - a_0\,b_1)\,b_1 = a_0\,b_1^2 - a_1\,b_0\,b_1 + a_2\,b_0^2 \notag \end{eqnarray}\] \[\begin{eqnarray} && f = a\,x +b\,y + p = a\,x + (b\,y + p)\notag \\ && g = c\,x + d\,y + q = c\,x + (d\,y + q)\notag \end{eqnarray}\] ◆ 実行例
/home/inoue/bin/go tmp_lang/chunk-79.mx > tmp_lang/chunk-79.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-79.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-79.mx
eq1:a0+a1*x+a2*x^2
2
a2 x + a1 x + a0
eq2:b0+b1*x
b1 x + b0
resultant(eq1,eq2,x)
2 2
a0 b1 - a1 b0 b1 + a2 b0
"/* 注:終結式は次の bezout() の結果を用いて計算できる */"
bezout(eq1,eq2,x)
[ a2 b0 a1 b0 - a0 b1 ]
[ ]
[ b1 b0 ]
eq1:expand((x-1)*(x-2))
2
x - 3 x + 2
eq2:expand(x-3)
x - 3
eq3:expand(x-2)
x - 2
resultant(eq1,eq2,x)
2
bezout(eq1,eq2,x)
[ - 3 7 ]
[ ]
[ 1 - 3 ]
resultant(eq1,eq3,x)
0
bezout(eq1,eq3,x)
[ - 2 4 ]
[ ]
[ 1 - 2 ]
/var/www/html/LANG/tmp_lang/chunk-79.mx次に,2変数関数 \(f(x,\,y), ~ g(x,\,y)\) を,変数\(x\) に関する1変数関数と 見なし,それらの終結式を求める.この結果を用いて,変数消去を行える.そ のような例を以下に示す.\ 例2.2変数関数の変数消去 \[\begin{eqnarray} {\rm res}(f,\,g,\,x) &=& \left|\matrix{ a & b\,y+p \cr c & d\,y+q \cr } \right| = a\,(d\,y+q) - c\,(b\,y+p) \notag \\ &=& (a\,d-b\,c)\,y + a\,q - c\,p \notag \end{eqnarray}\]
(%i3) :lisp $ts;
((MRAT SIMP (((%SIN SIMP) $X) $X) (sin(x)13183 X13184)
(($X ((10 . 1)) 0 NIL X13184 . 2)) TRUNC)
PS (X13184 . 2) ((10 . 1)) ((1 . 1) 1 . 1)
((3 . 1) -1 . 6) ((5 . 1) 1 . 120)
((7 . 1) -1 . 5040) ((9 . 1) 1 . 362880))
(%i3) :lisp $ps;
((%SUM SIMP)
((MTIMES SIMP) ((MEXPT SIMP) -1 $I1)
((MEXPT SIMP) ((MFACTORIAL SIMP)
((MPLUS SIMP) 1 ((MTIMES SIMP) 2 $I1))) -1)
((MEXPT SIMP) $X ((MPLUS SIMP) 1
((MTIMES SIMP RATSIMP) 2 $I1))))
$I1 0 $INF) ◆ 実行例
/home/inoue/bin/go tmp_lang/chunk-80.mx > tmp_lang/chunk-80.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-80.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-80.mx
eq1:a*x+b*y+p
b y + a x + p
eq2:c*x+d*y+q
d y + c x + q
resultant(eq1,eq2,x)
(- (b c - a d) y) + a q - c p
bezout(eq1,eq2,x)
[ (a d - b c) y + a q - c p ]
/var/www/html/LANG/tmp_lang/chunk-80.mx無平方因子分解
多項式因子 f が「無平方 (square free)」であるとは,定数と異なる多項式
g で \(g^2\) が f を
割り切るようなものが存在しないことをいう.特に,1変数多項式の場合には,f
と導関数 \(\frac{df}{dx}\) が
共通因子を持たないことをいう.
関数 sqfr(exp) を用いて exp を,無平方因子に分解する. 関数の名称 sqfr
は square free(無平方)に由良するが,square free 因子
を出力するわけではなく,多項式を平方因子を含まない項に因数分解する.
factor との違いを見てみる分かりやすい.
/home/inoue/bin/go tmp_lang/chunk-81.mx > tmp_lang/chunk-81.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-81.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-81.mx
display2d:false
c1:expand((x-1)^3*(x+1)^3*(x+2))
x^7+2*x^6-3*x^5-6*x^4+3*x^3+6*x^2-x-2
sqfr(c1)
(x+2)*(x^2-1)^3
factor(c1)
(x-1)^3*(x+1)^3*(x+2)
"/var/www/html/LANG/tmp_lang/chunk-81.mx"つまり,sqfr を実行した場合は \(x^2 -
1\)(square free)は因数分解されずに残る.
このような関数が用意されている理由は,一般に因数分解は困難であるが,square
free 因子を 見つけることは簡単だからである.
以下,参考までに square free 因子を見つける実験をおこなう. まず,関数
f[1] とその導関数 f’[1] との最大公約数 f[2] を求める. さらに,f[2] と
f’[2] の最大公約数 f[3] を求め …..、という作業を最大公約数が 1
になるまで繰り返す.:
/home/inoue/bin/go tmp_lang/chunk-82.mx > tmp_lang/chunk-82.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-82.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-82.mx
display2d:false
f[1]:expand((x-1)^3*(x+1)^3*(x+2))
x^7+2*x^6-3*x^5-6*x^4+3*x^3+6*x^2-x-2
f[2]:gcd(f[1],diff(f[1],x))
x^4-2*x^2+1
f[3]:gcd(f[2],diff(f[2],x))
x^2-1
f[4]:gcd(f[3],diff(f[3],x))
1
"/* 注:*/"
quotient(f[2],f[3]^2)
1
quotient(f[1],f[3]^3)
x+2
"/var/www/html/LANG/tmp_lang/chunk-82.mx"1 になる 1 つ手前 \(f[3] = x^2 - 1\)
に注目する. 一連の計算から,f[2] は \(x^2 -
1\) の2乗で割り切れ,f[1] は \(x^2 -
1\) の3乗で割り切れる. そこで,quotient(f[2], f[3]^2); および
quotient(f[1], f[3]^3); より,求める square free 因子は \(x^2 - 1\) と \(x
+ 2\) であるとこがわかる.
以下に,第2例を示す.
/home/inoue/bin/go tmp_lang/chunk-83.mx > tmp_lang/chunk-83.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-83.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-83.mx
display2d:false
f[1]:expand(x^5*(x+1)^2*(x-1)^2*(x+4))
x^10+4*x^9-2*x^8-8*x^7+x^6+4*x^5
f[2]:gcd(f[1],diff(f[1],x))
x^6-x^4
f[3]:gcd(f[2],diff(f[2],x))
x^3
f[4]:gcd(f[3],diff(f[3],x))
x^2
f[5]:gcd(f[4],diff(f[4],x))
x
f[6]:gcd(f[5],diff(f[5],x))
1
"/* 注1:*/"
quotient(f[2],f[5]^4)
x^2-1
quotient(f[1],%^2*f[5]^5)
x+4
"/* 注:*/"
sqfr(f[1])
x^5*(x+4)*(x^2-1)^2
"/var/www/html/LANG/tmp_lang/chunk-83.mx"注1までで,square free 因子の 1 つが f[5] = x であり、しかも f[1] が f[5] の 5 乗で割り切れることが分かる.さらに, 注2 により,f[1] の残りの square free 因子として、\(x^2 - 1\) と \(x + 4\) が求まる.最後に確認を行う:
/home/inoue/bin/go tmp_lang/chunk-84.mx > tmp_lang/chunk-84.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-84.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-84.mx
sqfr(expand((x-1)*(x-2)))
2
x - 3 x + 2
sqfr(expand((x-1)*(x-2)^2))
2
(x - 2) (x - 1)
sqfr(expand((x-1)*(x-2)*(x-3)))
3 2
x - 6 x + 11 x - 6
sqfr(expand((x-1)*(x-2)*(x-3)^2))
2 2
(x - 3) (x - 3 x + 2)
sqfr(expand((x-1)*(x-2)*(x-3)^5))
5 2
(x - 3) (x - 3 x + 2)
/var/www/html/LANG/tmp_lang/chunk-84.mx[専門的な文献]:整数係数多項式の因数分解法としては,指数時間アルゴリズムではあるけれども
多くの場合実用的な Berlekamp-Zassenhaus
法と多項式時間アルゴリズムではあるけれど遅い LLL 法が
良く知られている.
この論文では Berlekamp-Zassenhaus
法を改良し,実用的な多項式時間アルゴリズムが考案されている. すでに
Maple などにはこの方法が実装されている
(が,我々が日常的に扱う多項式ではその恩恵を受けることは無いと思われる)。
関数 sqfr
はこういったアルゴリズムを実装するためのスタート地点に相当するものである.
13. 級数について
13.1 級数データの扱い
\(c^{inf}\) − 可微分関数に対して,
taylor や powerseries で級数に変換が可能である. taylor と powerseries
の違いは, taylor が表示桁数を指定して, 級数に表示するのに対し,
powerseries はより一般的な級数として計算する.
以下に \(\sin(x)\) を原点を中心として
taylor() と powerseries() を使って 級数展開してみる. なお, taylor で x
の次数が 10 迄に制限している.
/home/inoue/bin/go tmp_lang/chunk-85.mx > tmp_lang/chunk-85.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-85.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-85.mx
ts:taylor(sin(x),x,0,10)
3 5 7 9
x x x x
/T/ x - -- + --- - ---- + ------ + . . .
6 120 5040 362880
ps:powerseries(sin(x),x,0)
inf
==== i1 2 i1 + 1
\ (- 1) x
> -----------------
/ (2 i1 + 1)!
====
i1 = 0
/var/www/html/LANG/tmp_lang/chunk-85.mxこの様に, taylor では x の羃の列となっているが, powerseries では多項式の和として表現されている. この二つのデータが内部表現, 即ち, LISP の側のデータがどの様に記述されているか調べてみよう. このデータを見る簡単な方法は, LISP の側からデータを見ることである. このために, :lisp 関数を使いる. :lisp 関数の引数として, LISP の S 式を与えると, Maxima は その結果を出力ラベルを付けずにそのまま表示する. Maxima のアトムの先頭に $ を付けたものが, LISP 側 のアトムに対応するので, ts のデータを見たければ, :lisp 関数の引数として $ts を与えれば良い.
\[\begin{eqnarray} f(x) &\doteq& \displaystyle\sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!}\,(x-x_0)^k \notag \\ &\doteq& f(x_0) + f^{(1)}(x_0)\,(x-x_0) + \frac{f^{(2)}(x_0)}{2}\,(x-x_0)^2 + \frac{f^{(3)}(x_0)}{3!}\,(x-x_0)^3 + \cdots \notag \end{eqnarray}\]
たデータになっていることが判る. 先ず, taylor は多項式の CRE 表現を拡張した表現となっているが, powerseries は 多項式の一般表現を利用したものになっている. この taylor や powerseries 関数とは逆に与えられた級数を函数に戻す関数として, nusum, revert や revert2 がある. ただし, numsum は漸化式, revert と revert2 は多項式近似以上のものではなく, 元の関数の復元が行えるとは限らない.
13.2 Taylor級数展開
1変数関数のTaylor級数展開
◆ \(f(x) = \sin(x)\) の \(x_0=0\) (原点) におけるTaylor展開 \[ \sin(x) \doteq x - \frac{x^3}{6} + \frac{x^5}{120} + \frac{x^7}{5040} + \cdots \]
/home/inoue/bin/go tmp_lang/chunk-86.mx > tmp_lang/chunk-86.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-86.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-86.mx
taylor(sin(x),x,0,7)
3 5 7
x x x
/T/ x - -- + --- - ---- + . . .
6 120 5040
/var/www/html/LANG/tmp_lang/chunk-86.mx◆ taylor 展開と関数近似
/home/inoue/bin/go tmp_lang/chunk-87.mx > tmp_lang/chunk-87.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-87.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-87.mx
display2d:false
define(f(x),sin(x))
f(x):=sin(x)
x0:0
plist:[1,3,5,7]
"/* 注: 上記次数の展開を求める */"
xmin:-%pi
xmax:%pi
funclist:[f(x)]
for i thru length(plist) do
(exp:taylor(f(x),x,x0,plist[i]),display2d:true,ldisplay(exp),
display2d:false,define(g[i](x),taytorat(exp)),
funclist:endcons(g[i](x),funclist))
(%t10)/T/ exp = x + . . .
3
x
(%t11)/T/ exp = x - -- + . . .
6
3 5
x x
(%t12)/T/ exp = x - -- + --- + . . .
6 120
3 5 7
x x x
(%t13)/T/ exp = x - -- + --- - ---- + . . .
6 120 5040
funclist
[sin(x),x,-(x^3-6*x)/6,(x^5-20*x^3+120*x)/120,
-(x^7-42*x^5+840*x^3-5040*x)/5040]
set_plot_option([gnuplot_term,png])
set_plot_option(['gnuplot_out_file,"Max-ref-2_files/fig13-1.png"])
gpreamble:"set key right bottom; set yrange [-1.1:1.1]; set zeroaxis;"
plot2d(funclist,[x,xmin,xmax],[legend,"sin(x)","1","3","5","7"],
[gnuplot_preamble,gpreamble])
"/var/www/html/LANG/tmp_lang/chunk-87.mx"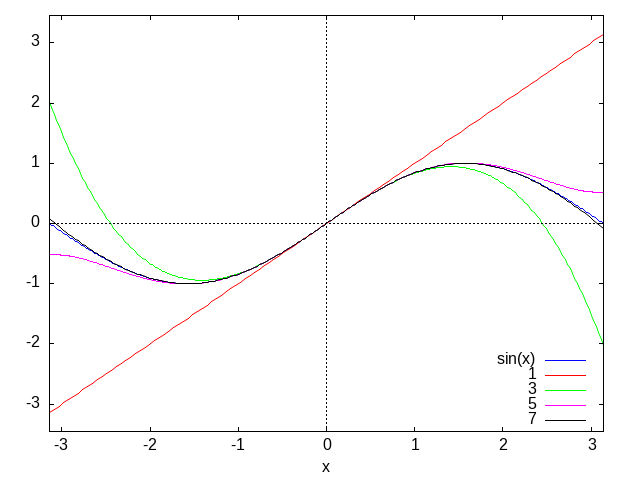
\[\begin{eqnarray} f(x) &\doteq& \sum_{k=0}^{n} \dfrac{1}{k!} f^{(k)}(x_0) (x - x_0)^k = \sum_{k=0}^{n} \dfrac{1}{k!} \left\{(x-x_0) \dfrac{d}{d x} \right\}^{k} f(x)_{x = x_0} \notag \end{eqnarray}\]
◆ taylor 展開の操作(1)
/home/inoue/bin/go tmp_lang/chunk-88.mx > tmp_lang/chunk-88.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-88.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-88.mx
c1:taylor(1/(1-x),x,0,3)
2 3
/T/ 1 + x + x + x + . . .
c2:taylor(1/(1-x),x,x0,2)
2
1 x - x0 (x - x0)
/T/ (- ------) + -------------- - ---------------------- + . . .
x0 - 1 2 3 2
x0 - 2 x0 + 1 x0 - 3 x0 + 3 x0 - 1
c2:mytaylor_simp(1/(1-x),x,x0,2)
1
mytaylor_simp(-----, x, x0, 2)
1 - x
/var/www/html/LANG/tmp_lang/chunk-88.mx◆ taylor 展開の操作(2)
asymp により負の冪で展開する.
/home/inoue/bin/go tmp_lang/chunk-89.mx > tmp_lang/chunk-89.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-89.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-89.mx
c3:taylor(1/(1-x),[x,0,3,asymp])
1 1 1
/T/ (- -) - -- - -- + . . .
x 2 3
x x
c4:taylor(sqrt(x+1),x,0,5)
2 3 4 5
x x x 5 x 7 x
/T/ 1 + - - -- + -- - ---- + ---- + . . .
2 8 16 128 256
c5:taytorat(c4)
5 4 3 2
7 x - 10 x + 16 x - 32 x + 128 x + 256
/R/ ------------------------------------------
256
/var/www/html/LANG/tmp_lang/chunk-89.mx◆ taylor 展開の操作(3)
/home/inoue/bin/go tmp_lang/chunk-90.mx > tmp_lang/chunk-90.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-90.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-90.mx
c6:taylor((x+1)^n,x,0,3)
2 2 3 2 3
(n - n) x (n - 3 n + 2 n) x
/T/ 1 + n x + ----------- + -------------------- + . . .
2 6
c7:product((1+x^i)^2.5,i,1,inf)/(1+x^2)
inf
/===\
! ! i 2.5
! ! (x + 1)
! !
i = 1
-----------------
2
x + 1
c8:ev(taylor(c7,x,0,3),keepfloat)
2 3
/T/ 1 + 2.5 x + 3.375 x + 6.5625 x + . . .
/var/www/html/LANG/tmp_lang/chunk-90.mx2変数関数のTaylor級数展開
- 1変数関数 \(f(x)\) の点 \(x_0\) におけるテイラー展開
\[\begin{eqnarray} f(x,~y) &\doteq& \displaystyle\sum_{k=0}^{n} \dfrac{1}{k!} \left\{(x-x_0) \dfrac{\partial}{\partial x} + (y-y_0) \dfrac{\partial}{\partial y}\right\}^{k} f(x,~y)_{(x,y) = (x_0,y_0)} \notag \\ &\doteq& f(x_0,y_0) \displaystyle + \left\{ f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)\right\} \notag \\ && \hspace{-5em} + \dfrac{1}{2!} \left\{ f_{xx}(x_0,y_0)(x-x_0)^2 + 2\,f_{xy}(x_0,y_0)(x-x_0)(y-y_0) + f_{yy}(x_0,y_0)(y-y_0)^2 \right\} \notag \end{eqnarray}\]
/home/inoue/bin/go tmp_lang/chunk-91.mx > tmp_lang/chunk-91.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-91.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-91.mx
f(x,y):=(1+y)*(1+sin(x))
out:taylor(f(x,y),[x,y],0,2)
/T/ 1 + (x + y) + y x + . . .
define(f2(x,y),out)
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-red-2_files/fig13-2a.png"])
plot3d(f(x,y),[x,-1,1],[y,-1,1],[gnuplot_pm3d,true],[grid,20,10])
set_plot_option([gnuplot_out_file,"Max-ref-2_files/fig13-2b.png"])
plot3d(f2(x,y),[x,-1,1],[y,-1,1],[gnuplot_pm3d,true],[grid,20,10])
/var/www/html/LANG/tmp_lang/chunk-91.mx
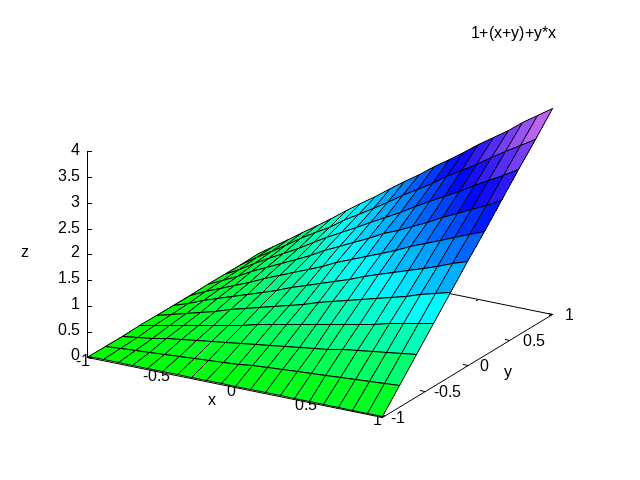
maxtayorder が true であれば, (切捨てられた)taylor 級数の代数操作中に, taylor は正確になる様に可能な限りの多くの項を保持しようとする.
psexpand が true であれば, 展開した有理関数式を広く展開したものを表示する.(ratexpand もこの処理をおこなう). false であれば, 多変数式が有理関数パッケージ内部で表示される.
psexpand:multi であれば, 全次数が n の変数の項で互いにグループ化される.
13.3 級数展開に関連する環境変数
● cauchysum:false
二つの無限和 (inf を上限として持つ和) の積で sumexpand が true,
cauchysum が true に設定されていれば, cauchy
積が通常の積の代りに用いられる. cauchy 積では,
内部和の添字が他と独立して変化する添字ではなく,
外側の添字変数の関数となる. 例えば,
sum(f(i),i,0,inf)sum(g(j),j,0,inf) は
sum(sum(f(i)g(j-i),i,0,j),j,0,inf) となる.
● maxtayorder:true
true であれば, 切詰められた taylor 展開の代数操作で taylor
が正確と確証されるまでの項を保持する.
● niceindicespref:[i,j,k,l,m,n]
niceindices が和や積で添数(添字変数)を探すために用いるリスト. 例えば,
niceindicespref:[q,r,s,r,index] の様にする. リストの添字を使い果すと,
q0, その次に q1 等々と試みる.
● powerdisp:false
true であれば, 逆の順序で項の和が表示される. この場合は,
多項式も切り詰められた羃級数の様に, 最低次数の項が最初に表示される.
● psexpand:false
true であれば, 拡張有理関数式は全体的に展開される (ratexpand
もこの原因となる). false であれば,
多変数式が丁度有理関数パッケージに含まれるものであるかの様に表示される.
psexpand:multi であれば, 同じ総次数で項が互いにまとめられる.
● taylordepth:3
零でない項がまだ存在すれば, pow*2 に達するまで taylor は g(var)
の展開の次数を倍にして行く. ここで n は変数 taylordepth[3]
の値である.
● taylor_logexpand:true
taylor 級数中の対数関数の展開を制御する. true であれば, 全ての log
は全面的に展開され, 対数関数の同一性に関連する零の判定問題は,
この展開の過程の邪魔にはならないが, この手法は分子の 情報を無視するので,
数学的に常に正しいとは限らない.
taylor_logexpand が false に設定されていれば, log
の展開は形式的羃級数を得る必要がある場合に 限られる.
● taylor_order_coecients:true
式中の係数の順序を制御する. デフォルト値で taylor
級数の係数は正規順序で並べられる.
● taylor_truncate_polynomials:true
false であれば, taylor
に入力される多項式は無限精度を持つものとして考えられる. そうでなければ,
切捨水準を基準として切捨てられる.
● verbose:false
true であれば, powerseries の実行状況を処理に沿って表示する.
13.4 級数展開に関連する関数
● deftaylor(func,exp)
任意の 1 変数関数 func に対し, 0 の近傍に於ける Taylor 級数として exp
を定める. exp はその 変数の多項式や sum 関数を用いたものでもかまわない.
deftaylor で与えられた情報を表示するために powerseries(f(x),x,0)
が使える.
/home/inoue/bin/go tmp_lang/chunk-92.mx > tmp_lang/chunk-92.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-92.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-92.mx
deftaylor(f(x),x^2+sum(x^i/(2^i*i!^2),i,4,inf))
[f]
powerseries(f(x),x,0)
inf
==== i1
\ x 2
> -------- + x
/ i1 2
==== 2 i1!
i1 = 4
taylor(exp(sqrt(f(x))),x,0,4)
2 3 4
x 3073 x 12817 x
/T/ 1 + x + -- + ------- + -------- + . . .
2 18432 307200
/var/www/html/LANG/tmp_lang/chunk-92.mx● niceindices(exp)
式expを取り,
和と積の全ての添数を変更して幾らかより判り易いものに変更する. 添数として
i が使え, i が内部式で用いられていれば, 適切な添数を見つけるまで
j,k,l,m,n,i0,i1,i2,i3,i4,… の順で添字を振っていく.
● nusum(exp, var, low, high)
R.W.Gosper による決定手順を用いた変数varに対する式expの不定和を計算する.
式expと潜在的な解は n 次の羃乗, 階乗, 二項係数, そして有理関数の積として
表現可能なものでなければならない. なお, ここでは定和と不定和という言葉を
定積分と不定積分の類似として用いている. 不定和を取るとは,
変数の複数の区間, 例えば 0 から inf へと云ったものではなく,
その上での和に対する近い公式を与えることを意味する. そのため,
二項級数の一般的な部分和に対し, 公式が存在しないので, nusum
は使えない.
● pade(taylor_series, numer_deg_bound, denom_deg_bound) 有理関数のリストを返す. この有理関数は taylor 展開で分子と分母の次数の和が taylor 級数展開の切捨て 水準以下のものとなっている. 即ち, 返却される有理関数はあくまでも与えられた taylor 展開の有理関数による 最上の近似で, 指定した次数の上限を満すものになる. 最初の引数は単変数の taylor 級数, 第二と第三の引数は正整数であり, 近似有理関数の分子と分母の 次数の上限を定める. なお, pade の最初の引数は laurent 級数でもかまわない. この場合, 総次数が羃級数の長さ以下の全ての有理関数が返される. なお, ここでの (総次数 = 分子の次数 + 分母の次数), 級数の長さ = 切捨ての水準 + 1 - min(0, 級数の次数) となる.
/home/inoue/bin/go tmp_lang/chunk-93.mx > tmp_lang/chunk-93.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-93.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-93.mx
ff1:taylor(1+x+x^2+x^3,x,0,3)
2 3
/T/ 1 + x + x + x + . . .
pade(ff1,1,1)
1
[- -----]
x - 1
ff2:taylor((-(83787*x^10-45552*x^9+(-187296)*x^8+387072*x^7+86016*x^6
+(-1507328)*x^5+1966080*x^4+4194304*x^3
+(-25165824)*x^2+67108864*x-134217728))
/134217728,x,0,10)
2 3 4 5 6 7 8 9
x 3 x x 15 x 23 x 21 x 189 x 5853 x 2847 x
/T/ 1 - - + ---- - -- - ----- + ----- - ----- - ------ + ------- + -------
2 16 32 1024 2048 32768 65536 4194304 8388608
10
83787 x
- --------- + . . .
134217728
pade(ff2,4,4)
[]
/var/www/html/LANG/tmp_lang/chunk-93.mxこの羃級数表現では分子/分母の次数が 4 の有理関数を持たない. 一般的に, 未知係数を解くために十分なだけの分子と分母の次数が, 少なくとも足し合わせて羃級数の次数に 到達するものを持っていなければならない.
/home/inoue/bin/go tmp_lang/chunk-94.mx > tmp_lang/chunk-94.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-94.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-94.mx
ff2:taylor((-(83787*x^10-45552*x^9+(-187296)*x^8+387072*x^7+86016*x^6
+(-1507328)*x^5+1966080*x^4+4194304*x^3
+(-25165824)*x^2+67108864*x-134217728))
/134217728,x,0,10)
pade(ff2,5,5)
5 4 3 2
[- (520256329 x - 96719020632 x - 489651410240 x - 1619100813312 x
5 4
- 2176885157888 x - 2386516803584)/(47041365435 x + 381702613848 x
3 2
+ 1360678489152 x + 2856700692480 x + 3370143559680 x + 2386516803584)]
/var/www/html/LANG/tmp_lang/chunk-94.mx● powerseries(exp, var, point)
点point (無限の場合は inf) の近傍で,
変数varに対する式expの一般的な級数展開を生成する. なお, powerseries
で式を展開出来なければ, taylor
関数で級数の最初の幾つかの項を求められるかも しれない. なお, verbose を
true にしていると, 以下の様な進行状況が表示される.
/home/inoue/bin/go tmp_lang/chunk-95.mx > tmp_lang/chunk-95.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-95.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-95.mx
verbose:true
powerseries(log(sin(x)/x),x,0)
trigreduce: failed to expand.
sin(x)
log(------)
x
trigreduce: try again after applying rule:
d sin(x)
/ -- (------)
sin(x) [ dx x
log(------) = I ----------- dx
x ] sin(x)
/ ------
x
powerseries: first simplification returned
x
/
[ csc(g20711) sin(g20711) - g20711 cos(g20711) csc(g20711)
- I -------------------------------------------------------- dg20711
] g20711
/
0
powerseries: first simplification returned
g20711 cot(g20711) - 1
- ----------------------
g20711
powerseries: attempt rational function expansion of
1
------
g20711
inf
==== i2 2 i2 - 1 2 i2
\ (- 1) 2 bern(2 i2) x
> ----------------------------------
/ i2 (2 i2)!
====
i2 = 1
/var/www/html/LANG/tmp_lang/chunk-95.mx● revert(exp, var)
● revert2(exp, var, order)
taylor 級数から式expを多項式で復元する. 変数varは taylor
展開で用いた変数で, 0 の近傍での taylor 展開に対してのみに使える.
revert では taylor
級数の表示されている項を最高次数とする多項式にまとめてしまうが, revert2
では表示されていなくても, 指定した次数orderを越えない多項式にまとめる.
これら関数を利用するには, 予め load(revert)
を実行しておく必要がある.
/home/inoue/bin/go tmp_lang/chunk-96.mx > tmp_lang/chunk-96.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-96.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-96.mx
load("revert")
/usr/share/maxima/5.46.0/share/calculus/revert.mac
t1:taylor(sin(x),x,0,5)
3 5
x x
/T/ x - -- + --- + . . .
6 120
revert(t1,x)
5 3
9 x + 20 x + 120 x
/R/ --------------------
120
revert2(t1,x,10)
9 7 5 3
779 x 2 x 3 x x
------ + ---- + ---- + -- + x
25920 45 40 6
/var/www/html/LANG/tmp_lang/chunk-96.mx● taylor(exp, var, point, order)
式expを点pointの近傍で変数varの taylor 級数 (必要であれば laurent 級数)
として展開する. \(({\rm var} - {\rm
point})^{{\rm order}}\) までの項が生成される. ここで, 式expが
\(f(var)/g(var)\) の型で, \(g(var)\) に次数orderに達する項が無い場合,
taylor は \(g(var)\) を \(order * 2\) まで展開しようとする.
非零の項がまだ存在し, 変数 taylordepth の値が n であれば, \((order * 2)^n\) に達する迄, \(g(var)\) の展開の次数を倍にする.
taylor(exp,[var_1,point_1,order_1], [var_2,point_2,order_2],…)
は点point_i の近傍で 変数var_iの次数order_iで切り捨てられた羃級数を返す.
taylor(exp, [var_1, var_2,…], point, order).
ここで,
点pointと次数orderは変数のリストに対応するリストで置換えてもかまわない.
つまり, 各リストの n 番目の項目は互いに関連するものとなる. taylor(exp,
[var, point, order, asymp]) は (var - point)
の負の羃による式の展開を与える. 最も高い次数の項は \((var - point)^{-order}\) となる. asymp
は構文指定で変更が効かない. なお, 展開の制御は環境変数の taylor
logexpand が効力を持つ.
/home/inoue/bin/go tmp_lang/chunk-97.mx > tmp_lang/chunk-97.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-97.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-97.mx
c1:taylor(sin(x+2*y),[x,y],0,3)
3 2 2 3
x + 6 y x + 12 y x + 8 y
/T/ (2 y + x) - ---------------------------- + . . .
6
taylorinfo(c1)
[[x, y], [0, 0], [3, 3]]
c2:taylor(sin(x+2*y),[x,0,3],[y,0,3])
3 3
4 y 2 2 y 2
/T/ ((- ----) + 2 y + . . .) + (1 - 2 y + . . .) x + ((- y) + ---- + . . .) x
3 3
2
1 y 3
+ ((- -) + -- + . . .) x + . . .
6 3
taylorinfo(c2)
[[x, 0, 3], [y, 0, 3]]
/var/www/html/LANG/tmp_lang/chunk-97.mx● taylorinfo(exp)
式expが taylor 級数で無ければ false を返す. taylor 級数であれば, taylor 展開の項を記述するリストのリストが返される.
/home/inoue/bin/go tmp_lang/chunk-98.mx > tmp_lang/chunk-98.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-98.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-98.mx
ex:taylor((1-y)/(1-x),x,0,4,[y,a,inf])
/T/ ((1 - a) - (y - a)) + ((- (y - a)) + (1 - a)) x
2 3
+ ((- (y - a)) + (1 - a)) x + ((- (y - a)) + (1 - a)) x
4
+ ((- (y - a)) + (1 - a)) x + . . .
taylorinfo(ex)
[[x, 0, 4], [y, a, inf]]
/var/www/html/LANG/tmp_lang/chunk-98.mx● taylorp(exp)
述語関数であり, 式expが taylor 級数表現であるときに限って true
を返す.
● taylor_simplier(exp)
一引数の関数で, その引数は taylor
が羃級数の係数の簡約化で用いられる.
● taytorat(exp)
式expを taylor 形式から CRE 表現に変換する. つまり, rat(ratdisprep(exp))
に似ているが処理はより速いものになる.
/home/inoue/bin/go tmp_lang/chunk-99.mx > tmp_lang/chunk-99.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-99.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-99.mx
exp2:taylor(sin(x),x,0,10)
3 5 7 9
x x x x
/T/ x - -- + --- - ---- + ------ + . . .
6 120 5040 362880
exp3:taytorat(exp2)
9 7 5 3
x - 72 x + 3024 x - 60480 x + 362880 x
/R/ ------------------------------------------
362880
/var/www/html/LANG/tmp_lang/chunk-99.mxこの例で示す様に, ラベルが/T/から/R/に変化していることに注意する. 又, 内部表現も, CRE 表現に似た Taylor 級数展開から, X の多項式の CRE 表現に変換されていることにも注目する.
● trunc(exp)
一般表現の式expを切詰めた taylor 級数であるかの様に表示する.
/home/inoue/bin/go tmp_lang/chunk-100.mx > tmp_lang/chunk-100.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-100.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-100.mx
exp1:x^2+x+1
exp2:trunc(x^2+x+1)
is(exp1 = exp2)
true
/var/www/html/LANG/tmp_lang/chunk-100.mxこの例で示す様に, 表示は一見異なるが, exp1 = exp2 となり, データ自体に変化はない.
● unsum(func, n)
第一後退差分 \(func(n) - func(n−1)\)
を計算する.
/home/inoue/bin/go tmp_lang/chunk-101.mx > tmp_lang/chunk-101.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-101.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-101.mx
g(p):=(p*4^n)/binomial(2*n,n)
ex1:g(n^4)
4 n
n 4
----------------
binomial(2 n, n)
ex2:nusum(ex1,n,0,n)
4 3 2 n
2 (n + 1) (63 n + 112 n + 18 n - 22 n + 3) 4 2
------------------------------------------------ - ---
693 binomial(2 n, n) 231
unsum(ex2,n)
4 n
n 4
----------------
binomial(2 n, n)
/var/www/html/LANG/tmp_lang/chunk-101.mx14. 極限の計算
14.1 極限について
Maxima には,極限値を求める関数 limit() が用意されている. 一見すると
limit は代入と似たものに 見えるかもしれないが,
実際は全く異った操作である. 例えば, \(\sin(x)/x\) の原点での値を考えよう.
安易な代入では, \(0/0\)
となってしまって判らない. \(0/0\) や
\(\infty / \infty\) は不定形と呼ばれる.
これらは, 安易に割ってしまっては意味がないことが判る. さて, \(\sin(x) / x\) に話を戻す. この場合は \(\sin(x)\)
の原点周りの級数展開を考えると判り易くなる.
\[
\sin(x) = \sum_{i=0}^{\infty}\, (-1)^i\, \frac{1}{(2\,i + 1)!}\,
x^{2\,i+1}
\]
となり, これを \(x\) で割ってしまうと,
\(\frac{\sin(x)}{x} = 1 + x(羃級数)\)
となる.
以上から, \(x\) を 0 に近づけると 1
になることが判る.
Maxima で試してみる. Maxima には limit 関数があり, この関数は limit(関数, 変数, 値) で極限の計算が行える.
/home/inoue/bin/go tmp_lang/chunk-102.mx > tmp_lang/chunk-102.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-102.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-102.mx
limit(sin(x)/x,x,0)
1
/var/www/html/LANG/tmp_lang/chunk-102.mx\(\sin(x)/x\) のグラフを以下に示す.
/home/inoue/bin/go tmp_lang/chunk-103.mx > tmp_lang/chunk-103.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-103.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-103.mx
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-2_files/fig14-1.png"])
gpreamble:"set yrange [-0.5:1.1]; set xzeroaxis;"
plot2d(sin(x)/x,[x,-50,50],[gnuplot_preamble,gpreamble])
expt: undefined: 0 to a negative exponent.
plot2d: expression evaluates to non-numeric value somewhere in plotting range.
/var/www/html/LANG/tmp_lang/chunk-103.mx
図14.1. Max-ref-2_files/fig14-1.png
極限はこの様な計算を行なうが,
この近づけるという操作には方向を考えなければならない.
例えば, \(1 / x\) を考える. この関数は
\(x > 0\) では正値をとり, \(x < 0\) では負値をとり, \(x = 0\) が不連続点になっている.
/home/inoue/bin/go tmp_lang/chunk-104.mx > tmp_lang/chunk-104.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-104.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-104.mx
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-2_files/fig14-2.png"])
gpreamble:"set yrange [-10:10]; set zeroaxis ;"
plot2d(1/x,[x,-3,3],[gnuplot_preamble,gpreamble])
expt: undefined: 0 to a negative exponent.
plot2d: expression evaluates to non-numeric value somewhere in plotting range.
/var/www/html/LANG/tmp_lang/chunk-104.mx
図14.2. Max-ref-2_files/fig14-2.png
/home/inoue/bin/go tmp_lang/chunk-105.mx > tmp_lang/chunk-105.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-105.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-105.mx
limit(1/x,x,0)
infinity
limit(1/x,x,0,plus)
inf
limit(1/x,x,0,minus)
minf
/var/www/html/LANG/tmp_lang/chunk-105.mxこの様に右側から近づけた場合には正の無限大, 左側から近づけた場合には負の無限大となっている. この様に左右の極限が異なるので, limit(1/x,x,0) の結果は und となっている. limit では正の無限大は inf, 負の無限大は minf, 複素数での無限大は inty, 左右の極限が異なる 場合には und, 未定でも有界なものには ind といった表記を返す.
/home/inoue/bin/go tmp_lang/chunk-106.mx > tmp_lang/chunk-106.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-106.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-106.mx
limit(1/(x^2-1),x,1,plus)
inf
limit(1/(x^2-1),x,1,minus)
minf
limit(1/(x^2-1),x,1)
infinity
limit(sin(1/x),x,0)
ind
limit(1/(x^2+1),x,%i)
infinity
/var/www/html/LANG/tmp_lang/chunk-106.mx14.2 極限に関連する環境変数
● lhospitallim:4
limit で用いられる l’Hospital 則の適用回数の最大値. これは
limit(cot(x)/csc(x),x,0) の様な
場合に無限ループに陥いることを防ぐために用意されている.
● limsubst:false
limsubst は limit が未知の形式に代入を行うことを防ぎます. これは
limit(f(n)/f(n+1),n,inf) の様な もので, 1 となるバグを避けるためである.
limsubst が true であれば, この様な代入が許容される.
● tlimswitch:false
true であれば, 極限パッケージは可能なときに taylor 展開を利用する.
14.3 極限に関する関数
● limit(exp, var, value)
● limit(exp, var, value, direction)
limit は与えられた式expの極限を計算する.
また,変数varが値valueに近づく方向directionを 指定することもできる.
この場合, 変数が値に方向から接近する場合の式の極限を計算する. ここで,
方向は右極限なら plus, 左極限なら minus とし, 省略してもよい. 通常,
省略した場合は両側極限が計算される. なお, 原点の極限計算であれば zeroa
や zerob も使える. この場合は zeroa が原点の左側 (\(-\)側), zerob が原点の右側 (\(+\)側) から近付けることを意味する.
そのため, minus や plus の様な方向を指定する必要はない. 計算手法は,
Wang,p. の”Evaluation of denite integrals by symbolic manipulation”-
ph.d. thesis - Mac tr-92 October 1971. を参照すること.
limit は特別な記号として inf(正の無限大) と minf(負の無限大) を用いる.
出力では und(未定義), ind(不定だが有界) と innity(複素無限大)
が使われる場合がある. limit は inf-1
の様な定数式の簡約化で利用されることが多いため, 引数が唯一, 例えば,
limit(inf-1) の場合でも limit を使ってもよい.
● tlimit(exp, var, value)
● tlimit(exp, var, value, direction)
tlimswitch を true にした limit 関数である.
◆ 実行例
/home/inoue/bin/go tmp_lang/chunk-107.mx > tmp_lang/chunk-107.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-107.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-107.mx
limit(x*log(x),x,0,plus)
0
limit((x+1)^(1/x),x,0)
%e
limit(%e^x/x,x,inf)
inf
limit(sin(1/x),x,0)
ind
/var/www/html/LANG/tmp_lang/chunk-107.mx15 微分
15.1 予備知識
15.1.1 導関数と偏導関数
関数 \(f(x)\) の導関数 \[ f'(x) = \displaystyle\lim_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x} = \dfrac{d}{d x} f(x) \]
関数 \(f(x,\,y)\) の偏導関数 \[ f_x(x,\,y) = \displaystyle\lim_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x,~y) - f(x,~y)}{\Delta x} = \dfrac{\partial}{\partial x} f(x,~y) \] \[ f_y(x,~y) = \displaystyle\lim_{\Delta y \rightarrow 0} \dfrac{f(x,~y + \Delta y) - f(x,~y)}{\Delta y} = \dfrac{\partial}{\partial y} f(x,~y) \]
15.1.2 微分と全微分
- 微分 : \(dy = f'(x) dx\) \[\begin{eqnarray} && \quad \leftarrow~ z - z_0 = f_x(x_0,~y_0) (x - x_0) + f_y(x_0,~y_0) (y - y_0) \notag \\ && (置換 : z ~\rightarrow~ z + dz,~ z_0 ~\rightarrow~ z, \quad y ~\rightarrow~ y + dy,~ y_0 ~\rightarrow~ y, \quad x ~\rightarrow~ x + dx,~ x_0 ~\rightarrow~ x) \notag \end{eqnarray}\]
式 の添字された任意のオブジェクトの微分は追加引数として加えられた 変数 i を持つ. 全ての微分の添字は蓄えられる.
変数i は 1 から環境変数 dimension[デフォルト値:4] までの整数が指定できる. これでリスト coordinates の i 番目の要素で微分が実行され, その coordinates は座標系の名前のリスト, 例えば, [x,y,z,t] の様に, 設定されていなければならない. coordinates にアトムの変数が設定されていれば, 変数は vi によって添字され, 微分の変数として利用される. これは座標系の名前か,x[1], x[2],… の様に添字された名前の配列が使える. coordinates が指定された値を持っていなければ, 変数は上述の (1) として扱われる.
◆ 実行例:1変数関数\(f(x)\)の微分
/home/inoue/bin/go tmp_lang/chunk-108.mx > tmp_lang/chunk-108.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-108.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-108.mx
diff(sin(a*x+b),x)
a cos(a x + b)
diff((a*x+b)^3,x)
2
3 a (a x + b)
diff((a*x+b)^3,x,2)
2
6 a (a x + b)
"/* 注: k階微分 */"
diff((a*x+b)^3,x,k)
k
d 3
--- ((a x + b) )
k
dx
/var/www/html/LANG/tmp_lang/chunk-108.mx◆ 実行例:2変数関数\(f(x,\,y)\)の微分(偏微分,全微分)
/home/inoue/bin/go tmp_lang/chunk-109.mx > tmp_lang/chunk-109.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-109.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-109.mx
z:sin(a*x+b*y)
zx:diff(z,x)
a cos(b y + a x)
zy:diff(z,y)
b cos(b y + a x)
dz:diff(z)
b cos(b y + a x) del(y) + a cos(b y + a x) del(x) + y cos(b y + a x) del(b)
+ x cos(b y + a x) del(a)
zxx:diff(z,x,2)
2
- a sin(b y + a x)
zxy:diff(z,x,1,y,1)
- a b sin(b y + a x)
zyy:diff(z,y,2)
2
- b sin(b y + a x)
z:(a*x+b*y)^3
zx:diff(z,x)
2
3 a (b y + a x)
zy:diff(z,y)
2
3 b (b y + a x)
dz:diff(z)
2 2 2
3 b (b y + a x) del(y) + 3 a (b y + a x) del(x) + 3 y (b y + a x) del(b)
2
+ 3 x (b y + a x) del(a)
/var/www/html/LANG/tmp_lang/chunk-109.mx15.2 微分に関連する環境変数
● dependencies:[]
依存性を持つアトムのリストである. 依存性は depends, 或いは gradef
関数で設定できる.
● derivabbrev:false
true であれば, 微分は下添字として表示される.
この環境変数は単純に微分の表示にのみに影響する.
/home/inoue/bin/go tmp_lang/chunk-110.mx > tmp_lang/chunk-110.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-110.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-110.mx
diff(f(x),x)
d
-- (f(x))
dx
derivabbrev:true
true
diff(f(x),x)
(f(x))
x
/var/www/html/LANG/tmp_lang/chunk-110.mx● derivsubst:false
微分を含む項の代入の制御を行なう. 例えば, \(\displaystyle \frac{d^2\,y}{d\,t^2}\) は
\(y\) の \(t\) による2階微分であるが, \(\displaystyle \frac{d\,y}{d\,t}\) を \(x\) で置き換えれば, \(\displaystyle \frac{d\,x}{d\,t} =
\frac{d}{d\,t}\left(\frac{d\,y}{d\,t}\right)\) となる. derivsubst
は名詞形の微分を含む式に対し,
この様な置換を行うかどうかを制御する.
false の場合, susbst 関数による置換は出来ないが, true
の場合は許容する.
/home/inoue/bin/go tmp_lang/chunk-111.mx > tmp_lang/chunk-111.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-111.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-111.mx
derivsubst
false
subst(x,'diff(y,t),'diff(y,t,2))
2
d y
---
2
dt
derivsubst:true
subst(x,'diff(y,t),'diff(y,t,2))
dx
--
dt
subst(x,'diff(y,t),2*t+t^2*'diff(y,t,2))
2 dx
t -- + 2 t
dt
/var/www/html/LANG/tmp_lang/chunk-111.mx● gradefs:[]
gradef 関数で勾配を与えた関数のリストである.
15.3 微分に関係する関数
● antidi(g, x, u(x))
● antid(g, x, u(x))
antidi は任意の未定義関数とその導関数を含む式の積分を評価する.
例えば, antidi(g,x,u(x)) とすると,g は関数 u(x)
とその微分を含む式の積分が求めるものになる. x による antidi
を利用するためには load(antid) を予め実行しておく. 関数 nonzeroandfreeof
と linear も antid と同様に antid は antidi と同様であるが,
二つの成分のリストを返す点で異なる. また,
そのリストの最初の成分は式を積分したもので, 2番目の
成分は残りの微分不能な成分になる.
/home/inoue/bin/go tmp_lang/chunk-112.mx > tmp_lang/chunk-112.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-112.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-112.mx
load("antid")
expr:exp(z(x))*diff(z(x),x)*y(x)
z(x) d
%e y(x) (-- (z(x)))
dx
a1:antid(expr,x,z(x))
z(x) z(x) d
[%e y(x), - %e (-- (y(x)))]
dx
a2:antidiff(expr,x,z(x))
/
z(x) [ z(x) d
%e y(x) - I %e (-- (y(x))) dx
] dx
/
a2-(first(a1)+'integrate(second(a1),x))
0
antid(expr,x,y(x))
z(x) d
[0, %e y(x) (-- (z(x)))]
dx
antidiff(expr,x,y(x))
/
[ z(x) d
I %e y(x) (-- (z(x))) dx
] dx
/
/var/www/html/LANG/tmp_lang/chunk-112.mx● cartan
微分形式の外積は Elie Cartan により発展した微分幾何学の基本的な道具で,
偏微分方程式論でも 重要な適用こと例を持っている. 現行の Maxima
での実装は F.B.Estabrook と W.H.Wahlquist による.
プログラムは自己説明的なもので, batch(“cartan”); を実行すれば使える.
● delta(t)
Dirac のデルタ関数である. なお, laplace
関数のみがデルタ関数を認識している.
/home/inoue/bin/go tmp_lang/chunk-113.mx > tmp_lang/chunk-113.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-113.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-113.mx
assume(a < 0)
laplace(delta(t-a)*sin(b*t),t,s)
0
/var/www/html/LANG/tmp_lang/chunk-113.mxこの例では変数 a に関して何らの仮定や割り当てが無いために, “Is a positive, negative, or zero?” と Maxima が尋ねている. assume を用いて \(a < 0\) と仮定した場合を以下に示す.
● depends(funcL_1, varL_1,…, funcL_n, varL_n)
diff で用いる変数に関数の従属性を宣言する.
/home/inoue/bin/go tmp_lang/chunk-114.mx > tmp_lang/chunk-114.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-114.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-114.mx
depends(neko,[tama,mike])
[neko(tama, mike)]
diff(neko,tama)
dneko
-----
dtama
diff(diff(neko,tama),tama)
2
d neko
------
2
dtama
depends([rat1,rat2],[cheese,milk])
[rat1(cheese, milk), rat2(cheese, milk)]
depends([rat1,rat2],[cheese,milk],neko,[tama,mike])
[rat1(cheese, milk), rat2(cheese, milk), neko(tama, mike)]
/var/www/html/LANG/tmp_lang/chunk-114.mx勿論, depends を実行していなければ, diff で 0 になる. depends で neko が tama と mike を 変数とする関数と宣言したために, 微分を行っても零にならない. 最初の例では関数 neko が 1 成分しかないために, リストの大括弧を外している. 関数の変数に対する従属性は deoendencies に登録された函数の情報から調べることができる. 次の例では, f と g が x と y に, r と s が u, v と w に依存し, u が t に従属することを diff に 報せるために, depends([f,g],[x,y],[r,s],[u,v,w],u,t) としている.
/home/inoue/bin/go tmp_lang/chunk-115.mx > tmp_lang/chunk-115.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-115.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-115.mx
dependencies
[]
depends([f,g],[x,y],[r,s],[u,v,w],u,t)
[f(x, y), g(x, y), r(u, v, w), s(u, v, w), u(t)]
dependencies
[f(x, y), g(x, y), r(u, v, w), s(u, v, w), u(t)]
diff(r . s,u)
dr ds
(--) . s + r . --
du du
diff(r . s,t)
dr du ds du
(-- --) . s + r . (-- --)
du dt du dt
/var/www/html/LANG/tmp_lang/chunk-115.mxこの例では, depends を実行することで, dependencies に depends
で従属性を宣言した関数が変数と
一緒にリストに加えられていることに注目する. 又,
微分では合成関数の微分もできる. depends で設定した従属性は, remove
関数を使って削除することができる. 上の例の (%i11) で宣言した r の u
に対する従属性を削除したければ, remove(r,dependency) と入力する.
diff は dependencies に設定された情報を用いる. 積分, laplace
変換等での引数は, integrate(f(x),x) の様に,
従属性を関数内部で明確に与えなければならない.
● derivdegree(exp, dependent_var, independent_var)
式exp中の独立変数independent_varに対する
従属変数dependent_varの微分で最も高い階数を見つける.
/home/inoue/bin/go tmp_lang/chunk-116.mx > tmp_lang/chunk-116.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-116.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-116.mx
ex:'diff(y,x,2)+'diff(y,z,3)*2+'diff(y,x)*x^2
derivdegree(ex,y,x)
2
/var/www/html/LANG/tmp_lang/chunk-116.mxこの様に名詞型の入力に対し, 最高階数を探す. なお, 微分を名詞型で入力していなければ評価された式で 返されるため, 希望する値が返ってこないので注意が必要である.
● derivlist(var_1, … ,var_k)
ev 命令内部で,derivlist
で指定した変数var_1,…,var_kに対してのみ微分を行なう.
● diff(exp, var_1, order_1, … ,var_n, order_n)
diff は各変数var_iで各々階数order_iの式の微分を行なう. 1 変数による 1
階微分の場合は, diff(exp, var) の書式でかまわない.
関数の名詞型が要求される場合 (例えば, 微分方程式を記述するとき),
’diff を用いなければならない. この場合, デフォルトの表示は二次元的
(プリティプリント) 書式になる. ここで, deriveabbrev が true であれば,
微分は添字で表示される.
diff(exp) は全微分を与える. 即ち, 式expの各変数に対する微分と,
各変数の関数の del との積の和になる. 例えば, diff(sin(x*y));
を実行すると x cos(x y) del(y) + y cos(x y) del(x) が返される.
/home/inoue/bin/go tmp_lang/chunk-117.mx > tmp_lang/chunk-117.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-117.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-117.mx
diff(exp(f(x)),x,2)
2
f(x) d f(x) d 2
%e (--- (f(x))) + %e (-- (f(x)))
2 dx
dx
derivabbrev:true
ex:'integrate(f(x,y),y,g(x),h(x))
diff(ex,x)
h(x)
/
[
I (f(x, y)) dy + f(x, h(x)) (h(x)) - f(x, g(x)) (g(x))
] x x x
/
g(x)
/var/www/html/LANG/tmp_lang/chunk-117.mx\begin{figure}[htb]
● dscalar(func)
スカラ値関数に対し, スカラの d’Alembert の演算子を作用させる.
● express(exp)
偏微分の項の名詞型の微分を展開する. express は grad, div, curl や
laplacian といった演算子を 認識する. express は他に外積も認識する.
ただし, express では微分を名詞型で返すため, 実際の微分の 計算は ev
関数に ’diff オプションを付けて行なう. この関数を利用するためには予め
load(“vect”) を実行する.
/home/inoue/bin/go tmp_lang/chunk-118.mx > tmp_lang/chunk-118.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-118.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-118.mx
load(vect)
/usr/share/maxima/5.46.0/share/vector/vect.mac
e1:laplacian (x^2*y^2*z^2)
2 2 2
laplacian (x y z )
express(e1)
2 2 2
d 2 2 2 d 2 2 2 d 2 2 2
--- (x y z ) + --- (x y z ) + --- (x y z )
2 2 2
dz dy dx
ev(%,'diff)
2 2 2 2 2 2
2 y z + 2 x z + 2 x y
v1:[x1,x2,x3] ~ [y1,y2,y3]
[x1, x2, x3] ~ [y1, y2, y3]
express(v1)
[x2 y3 - x3 y2, x3 y1 - x1 y3, x1 y2 - x2 y1]
/var/www/html/LANG/tmp_lang/chunk-118.mx● gradef(f(x_1, … , x_m), g_1, … , g_n)
● gradef(f, x, exp)
関数 f の n 個の引数に対する微分を, \(\frac{d\,f}{d\,x_i} = g_i\) で定める.
もしも変数の総数数 m が 勾配の個数 n よりも小さい場合, 最初の f の i
番目の引数が参照される. x_iは関数定義で用いるダミー変数と同類で, 関数 f
の i 番目の変数を指定するために用いる. 最初の引数を除く全ての gradef
の引数は g が定義された関数ならば, その関数が呼び出され,
結果が用いられる. 勾配は関数が第一階微分を除いて正確に判らない場合で,
より高階の微分を得たいときに必要となる.
gradef(f, x, exp) は x による関数の微分が式expとなることを宣言する.
このとき, 自動的に depends(func, x) が実行される. gradef 関数はMaxima
の既に定義された関数の微分を再定義することにも使える. 例えば,
gradef(sin(x),sqrt(1-sin(x)^2)) の様にできる. ただし, 添字された関数に
gradef 関数は使えない.
gradef で勾配を定義すると, 環境変数 gradefs
にその関数の名前が蓄えられる. gradef
は関数に対する属性を設定する函数のため, 値は printprops で表示できる.
この場合, 属性は gradef となる. 又, アトムに対して宣言した場合には,
属性は atomgrad となる.
● ilt(exp, old_var, new_var)
新変数new_varと旧変数old_varに対する式expの逆 Laplace 変換を計算する.
式は分母が一次と二次の 因子を持った有理式でなければならない. ilt
の計算を効率的に行うためには有理式の展開を予め 実行しておくと良い.
laplace と ilt の両方を solve や linsolve と使うと, 単変数の微分方程式か
畳込み積分方程式を解くことができる.
/home/inoue/bin/go tmp_lang/chunk-119.mx > tmp_lang/chunk-119.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-119.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-119.mx
ex1:'integrate(sinh(a*x)*f(t-x),x,0,t)+b*f(t) = t^2
ex2:laplace(ex1,t,s)
a laplace(f(t), t, s) 2
--------------------- + b laplace(f(t), t, s) = --
2 2 3
s - a s
ex3:linsolve([ex2],['laplace(f(t),t,s)])
2 2
2 s - 2 a
[laplace(f(t), t, s) = --------------------]
5 2 3
b s + (a - a b) s
assume(a > 1 and b > 1 and a*b > 1)
ilt(rhs(first(ex3)),s,t)
sqrt(a) sqrt(a b - 1) t
2 cosh(-----------------------) 2
sqrt(b) a t 2
(- -------------------------------) + ------- + ------------------
3 2 2 a b - 1 3 2 2
a b - 2 a b + a a b - 2 a b + a
/var/www/html/LANG/tmp_lang/chunk-119.mx● laplace(exp, old_var, new_var)
旧変数old_varと新変数new_varに対する式expの Laplace 変換を計算する. 逆
laplace 変換は ilt である. 式expは多項式に関数 exp, log, sin, cos, sinh,
cosh と erf 関数を含むもの, atvalue の従属変数が
使われている定数係数の線形微分方程式でもかまわない.
初期条件は零で指定されていなければならないので,
他の一般解の何処かに押込める境界条件があれば,
その境界条件に対して一般解を求めて値を代入して定数消去ができる. 式には
畳込み (convolution integral) を含んでいてもよい. laplace
が適切に動作するために, 関数の従属性を明確に表示しなければならない.
つまり, 関数 f が x と y に従属 しているのであれば,
laplace(’di(f(x,y),x),x,s) の様に f が現れる 場合は常に f(x,y)
と記述する必要がある. なお, laplace は depends 命令で設定される
dependecies の影響を受けない.
/home/inoue/bin/go tmp_lang/chunk-120.mx > tmp_lang/chunk-120.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-120.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-120.mx
ex:laplace(%e^(2*t+a)*sin(t)*t,t,s)
a
%e (2 s - 4)
---------------
2 2
(s - 4 s + 5)
ilt(ex,s,x)
2 x + a
x %e sin(x)
/var/www/html/LANG/tmp_lang/chunk-120.mx● undi(exp)
微分が実行されれば,
添字されたオブジェクトの全ての微分を除いた式expと同値な式で,
その微分の引数が 添字付けられたものを生成する. 即ち, diff
関数の名詞型で置き換えたものに相当する. 微分され,
添字付けられた式をある関数定義で置き換え, ev(…,diff)
を指定して微分を実行したい場合には 便利である.
16 積分
16.1 Maxima での積分について
Maxima は記号積分, 数値積分の両方が行える. 積分に関しては, Risch の積分も不完全ながら実装されている. そのため, 単純に公式を当て嵌めるだけで積分の計算を行う様なシステムよりも 一段と優れた処理が行える. ただし, 積分の計算は微分と比べると格段に難しい問題のため, 比較的単純な式の計算でも思わぬ結果を得ることが ある. そのため, 記号積分の結果は何等かの形で検算を行うことを強く薦める. 最も簡単な方法は積分した結果を 微分して同じ結果が得られるかどうかを確認することである. Maxima で上手く計算出来ない簡単な式の例として, \(\displaystyle \sqrt{x + \frac{1}{x} - 2}\) を 挙げておく. この式は \(\displaystyle \sqrt{\frac{(x+1)^2}{x}}\) に変形できるが, この式の形の違いで 結果が大きく異なる.
/home/inoue/bin/go tmp_lang/chunk-121.mx > tmp_lang/chunk-121.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-121.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-121.mx
integrate(sqrt(x+1/x-2),x)
/
[ 1
I sqrt(x + - - 2) dx
] x
/
integrate(sqrt(factor(x+1/x-2)),x)
/
[ abs(x - 1)
I ---------- dx
] sqrt(x)
/
assume(x < 1 and x > 0)
[x < 1, x > 0]
integrate(sqrt(x+1/x-2),x)
3/2
2 x - 6 sqrt(x)
- ------------------
3
out1:integrate(sqrt(factor(x+1/x-2)),x)
3/2
2 x - 6 sqrt(x)
- ------------------
3
out2:diff(out,x)
0
ratsimp(out2)
0
/var/www/html/LANG/tmp_lang/chunk-121.mxこの例では, 同じ integrate でも \(\displaystyle \sqrt{\frac{(x+1)^2}{x}}\) の場合は, 名詞型を 返しており, 何も考えずに \(\displaystyle \frac{x-1}{\sqrt{x}}\) の計算を行ってはいない. 又, assume を使って, 条件 \(0 < x < 1\) を追加した場合でも, \(\displaystyle \sqrt{\frac{(x+1)^2}{x}}\) の integration の計算は間違っている. この様に Maxima の積分は正しい答を返すとは限らないが, 内部処理を適切に行うことで正しい答を得ることが 可能な場合もある. これは Maxima に限った話ではなく, 数式処理一般で記号積分の結果は面倒でも確認した方が 良い.何故, 式の形の違いで計算結果に違いが出るのか? これは結局, 式の並びの照合等によって処理を行っている ため, 式を変形していれば,並びも勿論異なるので, 照合の結果も異なり, それによって処理の流れが違うためで ある. これが数値の場合は, 式の並びは無関係で, 関数の値だけしか見ないため, この様な現象は累積誤差のことを 除くとまず生じない. 並び照合の結果が違っていても, 正しく処理が出来ていれば, 最終的に一致する筈であるが, この例の様に何処かの処理を間違えると当然結果が異なる. 数式積分では, 式を展開したり, factor で因子分解 する等で, 式を変形させて積分したもので結果を照合するのも正しい答を得るための有効な手段である. しかし, 実際はこれでも不十分なことがある. 例えば, \(\displaystyle \frac{3}{5-4\,\cos x}\) の積分 である.
/home/inoue/bin/go tmp_lang/chunk-122.mx > tmp_lang/chunk-122.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-122.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-122.mx
integrate(3/(5-4*cos(x)),x)
3 sin(x)
2 atan(----------)
cos(x) + 1
trigsimp(diff(%,x))
3 cos(x) + 3
----------------------
2
4 sin (x) + cos(x) + 1
/var/www/html/LANG/tmp_lang/chunk-122.mxこの様に一見すると正しい結果が出ている様である. でも間違っている. 何故なら被積分関数は滑かな連続関数で あるが, 結果の方は不連続な関数である. この様な例はグラフを利用して積分した関数を描くと一目で判る.
/home/inoue/bin/go tmp_lang/chunk-123.mx > tmp_lang/chunk-123.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-123.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-123.mx
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-2_files/fig16-1.png"])
gpreamble:"set yrange [0:3.2];"
plot2d(3/(5-4*cos(x)),[x,-10,10],[gnuplot_preamble,gpreamble])
set_plot_option([gnuplot_out_file,"Max-ref-2_files/fig16-2.png"])
gpreamble:"set yrange [-3:3]; set xzeroaxis ;"
plot2d(2*atan((3*sin(x))/(cos(x)+1)),[x,-10,10],[gnuplot_preamble,gpreamble])
/var/www/html/LANG/tmp_lang/chunk-123.mx
図16.1. Max-ref-2_files/fig16-1.png, fig16-2.png
integrate は被積分関数が f(g(x))*di(g(x),x) の形式であるかを, 幾つかの部分式 (例えば, 上の場合は g(x)) の微分で被積分関数が割れるかどうか検査する. 割切れると, f を積分表で探し, f の積分で g(x) を x の代りに代入する. ここで微分を取る際に勾配を用いる. 未知関数が被積分関数に現われれば, この段階で 消去されていなれければならない. そうでなければ, integrate は被積分関数の名詞型を返す.
integrate は被積分関数が特殊な手法, 例えば, 三角関数の代入と云った特定の手法が使える形式に適合するか どうかを試みる.
最初の二段階が失敗すると risch のアルゴリズムが利用される. 関数の相互関係は integrate が正確に 動作する様に厳密に表現されている必要がある. integrate で risch の積分を強制的に行わせることが可能 である. これは以下の様に ev を用いる.
グラフを描いて見るのも非常に有効な手段のひとつである. Maxima は積分処理のための関数を幾つか持っている. その中でも, integrate 関数は最も使われる. antid は指定していない関数の積分操作 (そしてその微分も勿論 のこと) を行える. この integrate では不定積分も定積分も処理できる. 定積分だけであれば, defint 関数も ある. ただし,この関数は,区間内に極が存在する場合, その極を検出せずに安易に計算を行うため, 注意が必要で ある. ここで, defint の処理を簡単に説明しておく. 通常は integrate(lisp 内部では $integrate) で 用いられている sinint 関数を内部で呼び出し, その結果に上限と下限の値を代入している. sinint でも risch 積分を行なう rischint を呼び出すこともできるが, ev を用いて rischint を用いる様に 指定することが出来ない. この点を修正するためには dent.lisp の antideriv の修正が最低でも必要となる. defint や integrate による定積分の計算で, 下限や上限に記号や式が含まれている場合, その正負を尋ねて くることがある. この場合, 正であれば pos; , 負であれば neg; , 零であれば zero; と入力する. 更に, assume を用いて正負の指定を予め行なえば, Maxima はこの様な質問をしない.
/home/inoue/bin/go tmp_lang/chunk-124.mx > tmp_lang/chunk-124.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-124.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-124.mx
assume(a > 0 and a < 1)
[a > 0, a < 1]
integrate(sqrt(2*x-x^2),x,0,a)
2
(a - 1) sqrt(2 a - a ) + asin(a - 1) %pi
------------------------------------ + ---
2 4
/var/www/html/LANG/tmp_lang/chunk-124.mx数値計算の手法を用いる場合には, romberg の他に quanc8 がある. quanc8 の方が計算速度, 精度と 安定性で romberg に勝っていることが多いが, romberg の方が精度が良好な場合もある. 以下の \(\displaystyle \sqrt{2\,x -x^2}\) の積分の例では romberg が精度で勝り, \(\exp(-x)* \sin(x)\) の積分では計算速度で romberg が勝っている.
/home/inoue/bin/go tmp_lang/chunk-125.mx > tmp_lang/chunk-125.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-125.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-125.mx
showtime:all
Evaluation took 0.0000 seconds (0.0000 elapsed)
all
out1:romberg(sqrt(2*x-x^2),x,0,1)
Evaluation took 0.0200 seconds (0.0300 elapsed)
0.7853897937007632
out2:quanc8(sqrt(2*x-x^2),x,0,1)
Evaluation took 0.0000 seconds (0.0000 elapsed)
2
quanc8(sqrt(2 x - x ), x, 0, 1)
out3:integrate(sqrt(2*x-x^2),x,0,1)
Evaluation took 0.0400 seconds (0.0400 elapsed)
%pi
---
4
bfloat(out3)
Evaluation took 0.0000 seconds (0.0000 elapsed)
7.853981633974483b-1
bfloat(integrate(sqrt(2*x-x^2),x,0,1))
Evaluation took 0.0000 seconds (0.0100 elapsed)
7.853981633974483b-1
romberg(exp(-x)*sin(x),x,0,1)
Evaluation took 0.0000 seconds (0.0000 elapsed)
0.2458370426035679
bfloat(integrate(exp(-x)*sin(x),x,0,1))
Evaluation took 0.0000 seconds (0.0000 elapsed)
2.458370070002374b-1
Evaluation took 0.1000 seconds (0.1000 elapsed)
/var/www/html/LANG/tmp_lang/chunk-125.mx数値積分の方が上記の極を検出し易いこともあり, 両者の結果を比較するのも検算の方法としては良い. 全般的に Maxima は初等関数 (有理式, 三角関数, 対数, 指数) と多少の拡張 (error 関数, dilogarithm) で可積分なものに限定しているので, g(x) や h(x) の様な未知の関数の積分は 扱えない.
16.2 積分に関する環境変数
● erflag:true
false であれば, erf 関数が被積分関数の中に含まれていない場合, risch
が答に erf 関数を入れることを抑制する.
● integration_constant_counter
方程式の不定積分を行うと, 式に導入される積分定数 (integrationconstant)
が導入される. この積分定数は順番が付いており, この順番が
integration_constant_counter に記録される.
/home/inoue/bin/go tmp_lang/chunk-126.mx > tmp_lang/chunk-126.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-126.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-126.mx
integration_constant_counter
0
integrate(x = 0,x)
2
x
-- = %c1
2
integration_constant_counter
1
integrate(exp(x) = 0,x)
x
%e = %c2
integration_constant_counter
2
/var/www/html/LANG/tmp_lang/chunk-126.mx● rombergabss:0.0
romberg によって生成された値の列を y[0],y[1],y[2] 等とすると, romberg は
n 回の反復の後に, (大雑把に言えば) (abs(y[n]-y[n-1]) < rombergabs か
abs(y[n]-y[n-1])/(y[n]=0.0 であれば 1.0, それ以外は y[n] >
rombergtol). true であれば, 0.0b0 を返す. そのため, rombergabs が 0.0
であれば 相対誤差の検証が得られる.
この追加変数は小さな値域で積分計算を行いたいときに便利である. そこで,
小さな主要な値域で最初に積分することで相対的精度検証を用い,
後に続く残りの値域上の積分は 絶対的精度の検証で用いる.
integral(exp(-x),x,0,50) を数値的に 10000000 分の 1 の相対精度で計算
したいとする. n をカウンターとして,
どれだけの関数評価が必要とされたかを見られる様に次の関数を定義する.
/home/inoue/bin/go tmp_lang/chunk-127.mx > tmp_lang/chunk-127.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-127.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-127.mx
f(x):=(mode_declare(n,integer,x,float),n:n+1,exp(-x))
translate(f)
warning: encountered undefined variable n in translation.
block([rombergtol:1.0E-6,romberabs:0],n:0,romberg(f,0,50))
1.000000000488271
n
257
/var/www/html/LANG/tmp_lang/chunk-127.mxこの例では, n = 257 となっているので, 関数評価は 257 回となる. それから, 先ず最初に integral(exp(-x),x,0,10) を実行して rombergabs を 1.e-6* (この部分積分) に設定するという風に積分を実行する.
/home/inoue/bin/go tmp_lang/chunk-128.mx > tmp_lang/chunk-128.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-128.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-128.mx
f(x):=(mode_declare(n,integer,x,float),n:n+1,exp(-x))
block([rombergtol:1.0E-6,rombergabs:0,sum:0],n:0,sum:romberg(f,0,10),
rombergabs:sum*rombergtol,rombergtol:0,sum+romberg(f,10,50))
1.000000001234793
n
130
/var/www/html/LANG/tmp_lang/chunk-128.mx二番目の手法は二倍近く俊敏 (257 対 130) なことになる.
● rombergit:11
romberg 積分命令の精度は環境変数の rombergtol と rombergit で支配される.
romberg は, 隣り合った近似解での相対差が rombergtol
よりも小さければ値を返す. 諦める前に刻み幅の romgergit
を半分にして試行する.
● rombergmin:0
romberg による関数評価の最小数を制御する. romberg
はその第一引数を少なくとも 2^(rombergmin+2)+1
回評価する. これは通常の収束テストが時々悪い通り方をするときに,
周期的関数の積分に対して便利である.
● rombergtol:1.e-4
romberg 積分命令の精度は環境変数 rombergtol と rombergit が支配する.
romberg が結果を返すのは, 隣り合った近似解の相対差が rombergtol
以下になったときである. なお, 諦める前に刻み幅の rombergit
を半分にして試する.
16.3 積分に関連する関数
● changevar(exp, f(x, y), y, x)
式expに現われる全ての \(x\)
に対する積分で \(f(x, y) = 0\) を満す
\(y\)
を新しい変数とする変数変換を行なう.
/home/inoue/bin/go tmp_lang/chunk-129.mx > tmp_lang/chunk-129.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-129.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-129.mx
assume(1-x > 0)
romberg(%e^sqrt(1-x),x,0,1)
1.999952658084032
print("---以下は誤り例---")
---以下は誤り例---
assume(y > 0)
ex0:'integrate(%e^sqrt(1-x),x,0,1)
ex1:changevar(ex0,x+y^2-1,y,x)
0
/
[ y
- 2 I y %e dy
]
/
- 1
ev(ex1,risch)
- 1
- 2 (2 %e - 1)
/var/www/html/LANG/tmp_lang/chunk-129.mx上記の誤り例に注意する.
/home/inoue/bin/go tmp_lang/chunk-130.mx > tmp_lang/chunk-130.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-130.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-130.mx
ex1:'integrate(%e^sqrt(a*y),y,0,4)
assume(a > 0)
ex2:changevar(ex1,y-z^2/a,z,y)
0
/
[ abs(z)
2 I z %e dz
]
/
- 2 sqrt(a)
- ----------------------------
a
ev(ex2,'risch)
2 sqrt(a) 2 sqrt(a)
2 ((- 2 sqrt(a) %e ) + %e - 1)
- -----------------------------------------------
a
/var/www/html/LANG/tmp_lang/chunk-130.mxchangevar は総和(\(\sum\)) や積 (\(\prod\)) の添字の変更にも使える. この場合、添字の変更は単純なシフト だけで, 次数の高い関数には利用出来ない.
/home/inoue/bin/go tmp_lang/chunk-131.mx > tmp_lang/chunk-131.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-131.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-131.mx
ex1:sum(a[i]*x^(i-2),i,0,inf)
inf
====
\ i - 2
> a x
/ i
====
i = 0
changevar(ex1,i-2-n,n,i)
inf
====
\ n
> a x
/ n + 2
====
n = - 2
/var/www/html/LANG/tmp_lang/chunk-131.mx● dblint(’f, ’r, ’s, a, b)
Maxima のトップレベルで記述されたもので,
機械語コードに変換・翻訳された二重積分関数である. このパッケージの利用は
load(dblint); を用いる. 計算で x と y の両方向で simpson 則を用いる.
関数 f(x,y) は二変数関数で translate で変換されたものか, compile
で翻訳されたものでなければならない. \[
\int_{x=a}^{b}\int_{y=r(x)}^{s(x)} \, f(x,y)\, dy\,dx
\] 更に, r(x) と s(x) も各々が 1変数関数で変換か翻訳された関数で,
a と b は浮動点小数でなければならない. この関数は二つの環境変数を持ち,
それらは x と y の区間の分割数 :dblint_x,dblint_y を決める.
その両方の初期値は 10 で, 他の整数値 (2dblint_x+1 点が x
方向に計算され, y 方向は 2dblint_y+1 となる)
と独立して変更することかできる. この関数は x 軸を分割し, x
の各値に対して最初に r(x) と s(x) を計算する.そして, r(x) と s(x) の
間の y 軸を分割し, y 軸に沿って積分を simpson 則を用いて計算する.
それから, x 軸に沿った積分を関数の 値を y の積分で simpson
則を用いて計算する. この手順は色々な理由で数値的に不安定であるが,
それなりに 速い. しかし, 高周波成分を持った関数や特異点
(領域に極や分岐点) を持つ関数に対する適用は避けること. y の積分は r(x)
と s(x) がどれだけ離れているかに依存し, 距離 s(x)-r(x) が x
で急速に変化すれば, 様々な y
積分で異なった刻み幅を持つ切捨てによって重大な誤差が発生するかもしれない.
領域での収束性を改善するために dblint_x と dblint_y
を増すことも可能であるが, 計算時間が増大する. 関数値は保存されず,
その関数が非常に多くの時間を費すものであれば,
何かを変更すると再計算で待つ必要がある.
関数 f, r と s の両方は dblint を呼出すために, 最初に translate
で変換されたものか compile で翻訳 されたものでなければならない.
これは多くの場合で翻訳されたコードで最大の速度向上を目指した結果である.
● defint(exp, var, low, high)
定積分を実行する関数である. 内部的に integrate を利用しており,
原始函数を求めると, 単純に上限と下限の
値を代入したものの差を取るだけである. この処理では区間 (下限, 上限)
の式の極の判定を一切行わないので 注意が必要である. そのため,
数値的な計算手法を用いたければ defint よりも romberg を利用する.
● erf(x)
error 関数. この関数の微分は \(2\,e^{-x^2}/\sqrt{\pi}\) になる.
(第11節参照)
● integrate(exp, var)
● integrate(exp, var, low, high)
変数varに対する式expの積分を行なう. 原始関数の計算が出来ない場合,
名詞型の積分式を返す. integrate は次の3段階の手順に従う.
/home/inoue/bin/go tmp_lang/chunk-132.mx > tmp_lang/chunk-132.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-132.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-132.mx
out:ev(integrate(3^log(x),x),'risch)
log(3) log(x)
x %e
-----------------
log(3) + 1
trigsimp(out)
log(3) log(x)
x %e
-----------------
log(3) + 1
/var/www/html/LANG/tmp_lang/chunk-132.mxintegrate は depends 関数で設定される環境変数 dependencies
の影響を受けない. integrate は定積分の 計算もできる. この場合は dent
と同じ引数を取る. 即ち, integrate(exp, var, low, high) は変数varに
対する下限lowから上限highまでの式expの定積分を行なう. この計算では,
integrate(exp, var) で原始関数を 求めて
上限と下限の値を求めた原始関数に代入して,
単純にその差を取るという荒っぽい方法である. そのため,
定積分を行う区間内に極が存在しても, その検証は一切行われない.
この定積分では, 最初の integrate(exp, var)
の計算に失敗すると名詞型を返す. 広義の定積分では, 正の無限大に関して inf
を使い, 負の無限大には minf が使える. この inf と minf に関しては, -inf
や -minf は各々 minf や inf と 同値なものではないことに注意する. Maxima
の広義の積分や, その他の代入操作で inf や minf は普通に 使えるが, -inf
や -minf を用いると全く無意味な結果を得ることがあるので注意する.
形式的な積分(例えば,
幾つかの助変数に関してある数値を代入するまで計算出来ない積分)では,
名詞型の ’integrate を利用する. この際に,
積分形式の文字による表示が不要であれば, 環境変数 display2d
を false にすると, 一行で表示される.
Maxima で積分が出来ないことが,
直ちに常にその積分が閉形式で存在しないことを意味しない. 以下に示す例で
integrate は名詞型を返すが, その原始関数を簡単に見つけることができる.
例えば,
\(x^3 + x + 1 = 0\) の根で被積分関数を
\(\displaystyle \frac{1}{(x - \alpha)(x -
\beta)(x - \gamma)}\) の形式に書換えると計算ができる. ここで α,
β, γ は方程式の根になる. Maxima はこの同値な形式を積分を行なうが,
その積分は非常に複雑になる.
● ldefint(exp, var, low, high)
変数varの上限highと下限lowに関する式expの不定積分に対し, limit
を用いた評価を行ない, 式の定積分を 計算する. minf と inf
の扱いは注意しなければならない. 特に, -inf や -minf
の様に符号を付けて用いると
本来の結果と同値でも無意味な結果を得るので注意が必要である.
/home/inoue/bin/go tmp_lang/chunk-133.mx > tmp_lang/chunk-133.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-133.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-133.mx
ldefint(exp(-x)*sin(x),x,0,-minf)
1
-
2
ldefint(exp(-x)*sin(x),x,0,inf)
1
-
2
ldefint(exp(-x)*sin(x),x,minf,0)
1
- -
2
ldefint(exp(-x)*sin(x),x,-inf,0)
1
- -
2
/var/www/html/LANG/tmp_lang/chunk-133.mxなお, ldefint は内部的には極の判別を一切行わずに, 記号積分した結果に上限と下限を limit で代入する だけである. 一応, 右極限と左極限を下限と上限で取る様にしているが, 単純に上限に対しては ’minus, 下限に 対しては ’plus を内部的に付けるだけなので, 上限や下限で不連続になる関数の場合, 上限と下限の大小関係を 逆にして ldefint を 計算すれば無意味になる可能性がある. なお, defint や integrate で定積分を行う 場合は区間内での極限の判別も行っている. 而し, ldefint では sinint 関数を用いて機械的に記号積分を 行うだけである. そのため, 関数をいきなり ldefint を用いて積分したり, 結果の検証を省くことは 薦められない. 以下に安易な例を示す.
/home/inoue/bin/go tmp_lang/chunk-134.mx > tmp_lang/chunk-134.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-134.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-134.mx
d1:ldefint(1/x^2,x,-1,1)
- 2
d2:ldefint(1/x^2,x,0,1)
1
limit - - 1
x -> 0 x
d3:ldefint(1/x^2,x,-1,0)
1
(- limit -) - 1
x -> 0 x
d2+d3
- 2
/var/www/html/LANG/tmp_lang/chunk-134.mxこの例で示す様に, d1 の ldefint の結果は -2 となっている. これは maxima では \(1/x^2\) を パターンマッチングで安易に記号積分し, 区間の上限と下限の極限を取っているためである. これに対し, defint と integrate では極が存在するためにエラーを返している. この様に, ldefint を 用いる場合には被積分関数の連続性に関して defint や integrate 以上に注意が必要となる. なお, ldefint には zeroa, zerob が使える. 各々が 0 の右極限と 0 の左極限を表す.
/home/inoue/bin/go tmp_lang/chunk-135.mx > tmp_lang/chunk-135.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-135.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-135.mx
ldefint(1/x^2,x,zeroa,1)
1
limit - - 1
x -> 0+ x
ldefint(1/x^2,x,zerob,-1)
1
limit - + 1
x -> 0- x
/var/www/html/LANG/tmp_lang/chunk-135.mxただし, 1+’zeroa の様な使い方は出来ないので注意する. なお, ldefint は defint と同様に積分で risch 積分を用いることが出来ない. ただし, defint と 同様の修正を加えれば, ev を用いて risch 積分を 用いることが可能である.
● potential(gradient)
環境変数を用いる計算.
● potentialzeroloc:0
これは nonlist かその形式でなければならない.
● [indeterminatej=expressionj, indeterminatek=expressionk,…]
前者は後者の全ての右手側に対する非リスト式に同値であり,
指定された右手側は定積分の下限として用いられる.
積分の成功はそれらの変数と順序に依存する. potentialzeroloc
はデフォルト値として 0 が設定されている.
● quanc8(’function_name, low, high)
適応型積分器で share1;qq fasl にて利用可能. demo と usage
ファイルがある. この手法は newtoncotes 8-panel 求積法を用い, そして,
関数名 quanc8 は 3 か 4 個の引数のものが利用可能である.
絶対と相対エラーチェックが用いられている. 利用には load(“qq”);
を実行する.
● residue(exp, var, value)
変数varの値valueに対する式expの複素平面上での留数を計算する. なお,
留数は式expの laurent 級数展開に 於ける
(var-value)^(-1)の係数である.
/home/inoue/bin/go tmp_lang/chunk-136.mx > tmp_lang/chunk-136.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-136.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-136.mx
residue(s/(s^2+a^2),s,a*%i)
1
-
2
residue(sin(a*x)/x^4,x,0)
3
a
- --
6
/var/www/html/LANG/tmp_lang/chunk-136.mx● risch(exp, var)
risch アルゴリズムの transcendential case を用いて var に対する exp
の積分を行う (risch アルゴリズムで代数的な場合は実装されていない).
これは現在, integrate の主要部が処理出来ない
入れ子状態の指数関数と対数関数の場合の処理を行なう. integrate は,
これらの場合が与えられると自動的 に risch を適用する.
erflag:true が false であれば, 開始すべき導関数が無い場合に risch が erf
関数を答の中に導入することを避ける.
/home/inoue/bin/go tmp_lang/chunk-137.mx > tmp_lang/chunk-137.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-137.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-137.mx
d1:risch(x^2*erf(x),x)
2
3 2 - x
%pi x erf(x) + (sqrt(%pi) x + sqrt(%pi)) %e
-------------------------------------------------
3 %pi
ev(diff(d1,x),ratsimp)
2
x erf(x)
/var/www/html/LANG/tmp_lang/chunk-137.mxintegrate で risch 積分を強制的に利用するには ev を用いる: ev(integrate(3^log(x),x), ’risch); なお, defint 等ではこの指定が出来ないため, defint.lisp で定義されている関数 antideriv の修正が 必要になる.
● romberg(exp, var, low, high)
● romberg(exp, low, high)
romberg を利用するために任意のファイルを読込む必要は無く,
自動的に読込まれる.
例:
/home/inoue/bin/go tmp_lang/chunk-138.mx > tmp_lang/chunk-138.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-138.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-138.mx
showtime:true
Evaluation took 0.0000 seconds (0.0000 elapsed)
true
romberg(sin(y),y,1,%pi)
Evaluation took 0.0200 seconds (0.0200 elapsed)
1.540302306426815
f(x):=1/(x^5+x+1)
Evaluation took 0.0000 seconds (0.0000 elapsed)
romberg(f(x),x,1.5,0)
Evaluation took 0.0000 seconds (0.0000 elapsed)
- 0.7529384119070062
Evaluation took 0.0400 seconds (0.0400 elapsed)
/var/www/html/LANG/tmp_lang/chunk-138.mx例:
/home/inoue/bin/go tmp_lang/chunk-139.mx > tmp_lang/chunk-139.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-139.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-139.mx
f(x):=(mode_declare([function(f),x],float),1/(x^5+x+1))
translate(f)
[f]
romberg(f,1.5,0)
- 0.7529384119070062
/var/www/html/LANG/tmp_lang/chunk-139.mx最初の引数expは translate 関数で変換された関数か, compile 関数で翻訳された関数でなければならない (compile 関数で翻訳されていれば, flowonum を返すために宣言されていなければならない). 最初の引数が未だに変換されたものでなければ, romberg はそれを translate で変換せずにエラーを返す. 積分の精度は環境変数 rombergtol(デフォルト値 1.e-4) と rombergit(デフォルト値 11) で操作される. もし, 続く近似で相対誤差が rombergtol よりも小さければ romberg は結果を返す. 諦める前に romgergit 倍 の刻み幅を半分にして試みる. romberg が実行する反復と関数評価の数は romgergabs と rombergmin で制御 される. romberg は再帰的に呼び出されていても良く, それ故, 2重, 3重積分が実行できる.
例:
/home/inoue/bin/go tmp_lang/chunk-140.mx > tmp_lang/chunk-140.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-140.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-140.mx
assume(x > 0)
[x > 0]
d1:integrate(integrate((x*y)/(x+y),y,0,x/2),x,1,3)
3
log(-)
9 2 13
(- 9 log(-)) + 9 log(3) + ------ + --
2 3 3
ev(d1,numer)
0.8193023963959085
define_variable(x,0.0,float,"global variable in function f")
f(y):=(mode_declare(y,float),(x*y)/(x+y))
g(x):=romberg('f,0,x/2)
romberg(g,1,3)
0.8193022864324522
/var/www/html/LANG/tmp_lang/chunk-140.mxこの方法の長所は関数 f が他の目的, 例えば, プロットのために使えることである. 短所は関数 f とその 自由変数 x の両方に対する名前を考慮しなければならないことである. 即ち, 環境変数無しならば:
/home/inoue/bin/go tmp_lang/chunk-141.mx > tmp_lang/chunk-141.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-141.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-141.mx
g1(x):=(mode_declare(x,float),romberg((x*y)/(x+y),y,0,x/2))
romberg(g1,1,3)
0.8193022864324522
/var/www/html/LANG/tmp_lang/chunk-141.mxとなる. ここでの長所は簡潔さにある.
/home/inoue/bin/go tmp_lang/chunk-142.mx > tmp_lang/chunk-142.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-142.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-142.mx
q(a,b):=romberg(romberg((x*y)/(x+y),y,0,x/2),x,a,b)
q(1,3)
0.8193022864324522
/var/www/html/LANG/tmp_lang/chunk-142.mxこの方法はより簡潔なもので, 変数は romberg の文脈に含まれるために宣言される必要がない. 残念なことに, 多重積分での romberg の利用には非常に大きな短所がある. これは多重積分を表現することで幾何学的情報が 欠落するために膨大な特別な計算が必要とされるので, この方法は信頼出来ない. 環境変数 rombergtol と rombergit を正確に理解して使わなければならない. なお, romberg の上限と下限では, 内部計算で倍精度の 浮動小数点を用いているので, 多倍長精度 (bigoat) で変換した浮動小数点は使えない.
● tldent(exp, var, ll, ul)
tlimswitch が true に設定されている ldefint.
17 代数方程式
方程式は演算子 \(=\) を挟んで左右の \(=\) を持たない式が配置された式である. 例えば, \(x^2+2*x+1=0\) の様な 形になる. なお, \(=\) の左右の式は関数 lhs と rhs で取り出すことができる.
/home/inoue/bin/go tmp_lang/chunk-143.mx > tmp_lang/chunk-143.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-143.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-143.mx
eq1:x^2+2*x+1 = y^2
2 2
x + 2 x + 1 = y
lhs(eq1)
2
x + 2 x + 1
rhs(eq1)
2
y
/var/www/html/LANG/tmp_lang/chunk-143.mxこの例では方程式として \(x^2+2 x+1=y^2\) を eq1 に割当てており, lhs(eq1) で方程式の左側の \(x^2+2 x+1\), rhs(eq1) で方程式右側の \(y^2\) を各々取り出している. なお, lhs と rhs は演算子 \(=\) に対してのみ使える関数である. 他の二項演算子には使えない. Maxima では連立方程式も扱える. ここで連立方程式は [eq_1, … , eq_n] の様に, 複数の方程式で構成 されたリストで表す.
/home/inoue/bin/go tmp_lang/chunk-144.mx > tmp_lang/chunk-144.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-144.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-144.mx
display2d:false
eq2:[2*x^2-5*y = 1,x+y*x+y^2 = 4]
eq2[1]
2*x^2-5*y = 1
eq2[2]
y^2+x*y+x = 4
"/var/www/html/LANG/tmp_lang/chunk-144.mx"この例では, 二つの方程式 \(2 x^2 - 5 y = 1\) と \(x + y\, x + y^2 = 4\) から構成される方程式の リストを eq2 に割当てている. リストで表現するため, 一つの方程式を取り出す場合は, リストの成分の 取り出しと同じ方式で行なう. Maxima では与えられた方程式を, 厳密解, 近似解の二通りで解くことができる. 厳密解は数学的に厳密な解, 近似解は文字通りの真の解に対する近似である. 例えば, 方程式を \(x^2 - 2 = 0\) とすれば, \(x = \pm \sqrt{2}\) が厳密解, \(x = ±1.4142\) がその近似解となる. なお, 重複解を持つ方程式を解くと, 環境変数 multiplicities に重複度をリストとして設定する関数が 幾つかある. algsys では factor で与えられた方程式を因子分割し, 終結式を用いて不要な多項式を減らして 解を求めようとする.
17.1 使用例
◆ 実行例:2次方程式を解く
/home/inoue/bin/go tmp_lang/chunk-145.mx > tmp_lang/chunk-145.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-145.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-145.mx
solve(a*x^2+b*x+c = 0,x)
2 2
sqrt(b - 4 a c) + b sqrt(b - 4 a c) - b
[x = - --------------------, x = --------------------]
2 a 2 a
solve(x^2-5*x+6 = 0,x)
[x = 3, x = 2]
/var/www/html/LANG/tmp_lang/chunk-145.mx◆ 実行例:連立1次方程式を解く
/home/inoue/bin/go tmp_lang/chunk-146.mx > tmp_lang/chunk-146.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-146.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-146.mx
solve([x+2*y = 5,2*x+3*y = 8],[x,y])
[[x = 1, y = 2]]
/var/www/html/LANG/tmp_lang/chunk-146.mx◆ 実行例:解けない例
/home/inoue/bin/go tmp_lang/chunk-147.mx > tmp_lang/chunk-147.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-147.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-147.mx
solve(exp(x) = 3-x^2,x)
x x
[x = - sqrt(3 - %e ), x = sqrt(3 - %e )]
load(newton)
newton(exp(x)-3+x^2,0.8)
8.344868653087891b-1
"/* 注: グラフで見る */"
define(f0(x),exp(x))
define(f1(x),3-x^2)
set_plot_option([gnuplot_term,png])
set_plot_option(['gnuplot_out_file,"Max-ref-2_files/fig17-1.png"])
gpreamble:"set key left; set yrange [-1:4]; set zeroaxis;"
plot2d([f0(x),f1(x)],[x,-2,2],[gnuplot_preamble,gpreamble])
/var/www/html/LANG/tmp_lang/chunk-147.mx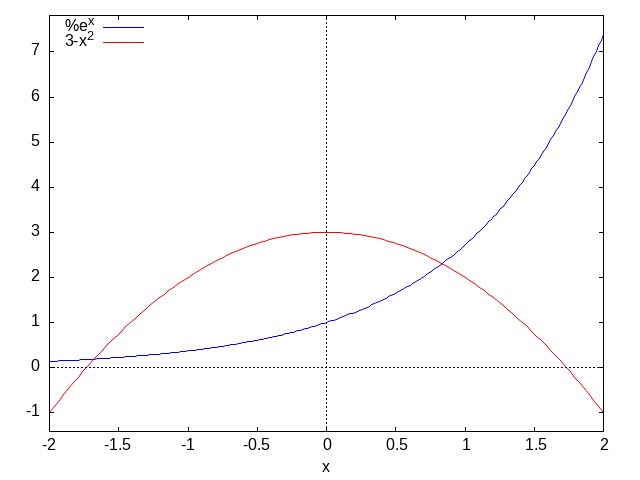
図17.1. Max-ref-2_files/fig17-1.png
◆ 実行例:不定方程式の例
/home/inoue/bin/go tmp_lang/chunk-148.mx > tmp_lang/chunk-148.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-148.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-148.mx
solve([2*x+4*y+(-3)*z = 30,x+y+z = 12],[x,y,z])
7 %r1 - 18 5 %r1 + 6
[[x = - ----------, y = ---------, z = %r1]]
2 2
/var/www/html/LANG/tmp_lang/chunk-148.mx◆ 実行例:不定方程式の例
/home/inoue/bin/go tmp_lang/chunk-149.mx > tmp_lang/chunk-149.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-149.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-149.mx
eq:x^6-6*x^4+13*x^2-2 = 0
"/* 注:solve() の返す結果の表示は省略する */"
out1:solve(eq,x)
"/* 注:algsys() の引数は,リストでなければならない */"
out2:algsys([eq],[x])
[[x = 1.786802359995863 - 0.5251544485445068 %i],
[x = 0.5251544485445068 %i + 1.786802359995863],
[x = (- 0.5251544485445078 %i) - 1.786802359995864],
[x = 0.5251544485445078 %i - 1.786802359995864], [x = 0.407736482825875],
[x = - 0.407736482825875]]
/var/www/html/LANG/tmp_lang/chunk-149.mx17.2 方程式に関連する環境変数
● %rnum_list:
変数 %r が algsys 関数で解に導入された場合, それらは %rnum_list
に生成された順番で追加される. これは後に解に代入するときに便利である.
concat(’%r, j) を実行するよりも, このリストを使うことを薦める.
● algexact:false
algsys 関数に影響を与える環境変数の一つである. true であれば, algsys は
solve を呼出し, realroots を常に利用する. false であれば,
終結式が単変数でない場合と quadratic か biquadratic な場合のみ solve
の呼出しをおこなう. algexact:true は厳密解のみを保証するものではなく,
algsys が最初に 厳密解を計算しようと試み, 最終的に, all
か失敗したときに近似解のみを生成する.
● algepsilon:108
algsys 関数で利用される定数である.
● backsubst:true
false ならば, 方程式を三角関数化した後の代入を防ぐ. これは,
後代入でとてつもなく大きな式が生成される様な 問題で必要となる.
● breakup:true
false であれば, solve
はデフォルト値の幾つかの共通部分式で構成されたものとしではなく,
一つの式として 3次又は2次の方程式の解の表示を行なう. ただし, breakup が
true となるのは programmode が false のときだけである.
● dispflag:true
false ならば, block 文の中で呼ばれた関数の出力表示を禁止する. 記号 $
のある block 文の末尾では dispflag を false に設定する.
● globalsolve:false
true の場合, 解かれた変数に解の値が実際に割当てられる.
/home/inoue/bin/go tmp_lang/chunk-150.mx > tmp_lang/chunk-150.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-150.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-150.mx
globalsolve:true
solve([xx*2+yy*3-1 = 0,xx+yy = 10],[xx,yy])
[[xx : 29, yy : - 19]]
xx
29
yy
- 19
globalsolve:false
solve([mm*2+nn*3-1 = 0,mm+nn = 10],[mm,nn])
[[mm = 29, nn = - 19]]
mm
mm
nn
nn
/var/www/html/LANG/tmp_lang/chunk-150.mxなお, globalsolve:true とした状態で, ある方程式を解いた後に同じ変数の方程式を解こうとすると次の エラーが出るので注意する. 例えば, 上記の例の (%i7) 行の方程式以下の行で置き換えた場合にはエラーに なる.
● linsolvewarn:true
false であれば, dependent equations
eliminated(従属方程式は消去された)
というメッセージ出 力が抑制される.
● insolve_params:true
true であれば, linsolve はまた記号 %ri を生成し, algsys
に記載された任意の助変数を表現するために 用いられる. false であれば,
以前の様に linsolve が動作する. 即ち, 不定方程式型に対し, 他の項の
幾つかの引数に対して解く.
● multiplicities:[not set yet]
solve や realroots で返される個々の解の重複度リストが設定される.
/home/inoue/bin/go tmp_lang/chunk-151.mx > tmp_lang/chunk-151.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-151.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-151.mx
multiplicities
not_set_yet
realroots(x^2-4 = 0,1.0E-5)
[x = - 2, x = 2]
multiplicities
[1, 1]
realroots(x^3-4*x^5 = 0)
1 1
[x = - -, x = -, x = 0]
2 2
multiplicities
[1, 1, 3]
/var/www/html/LANG/tmp_lang/chunk-151.mx● polyfactor:false
allroots で利用される環境変数である. polyfactor が true であれば,
polyfactor に与えられた多項式が 実係数多項式なら実数上で因子分解し,
係数に %i が含まれていれば複素数上で因子分解を行った結果を返す.
● programmode:true
false であれば, solve, realroots, allroots と linsolve が, %t ラベル
(中間行ラベル) に答を ラベル付けして出力する. true であれば, solve
等はリストの要素として答えを返す (programmode:false も 使われる. ただし,
backsubst が false に設定されたときを除く).
/home/inoue/bin/go tmp_lang/chunk-152.mx > tmp_lang/chunk-152.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-152.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-152.mx
programmode:false
false
solve(x^2+1,x)
solve: solution:
x = - %i
x = %i
[%t3, %t4]
programmode:true
solve(x^2+1,x)
[x = - %i, x = %i]
/var/www/html/LANG/tmp_lang/chunk-152.mx● realonly:false
true であれば, algsys は実数解, 即ち%i を持たない解のみを返す.
● rootsepsilon:1.0e-7
realroots
関数によって見つけられた根を含む確実な区間を設定する際に使う実数である.
● rootsmode:true
環境変数 rootsconmode は, true, false, all の値が設定可能で,
rootscontract に影響を与える. rootsconmode が false ならば,
rootscontract は wrt 有理数次数の分母が同じ次数のものだけを約分する.
true の場合, 次数の分母が割切れるもの同士のみ約分する. 例えば,
x^(1/6)*y^(1/8) の場合, 次数の分母の 8 と 6 に注目すると, 8 は 6
の倍数ではないため, rootscontract でこの項をまとめることは出来ない.
これに対し, x(1/4)y^(1/8) の場合は, 分母の 8 は 4
で割切れるため, rootscontract は (x^2y)(1/8) を返す. all
の場合, rootscontract は次数の分母の LCM を取ってまとめる.
● ieqnprint:true
ieqn 関数が返した結果の挙動を制御する. ieqnprint が false であれば, ieqn
関数によって返された リストは以下の形式となる.
最初に方程式を factor で因子分解し, 各因子から構成される部分系 system_i , 即ち, 方程式の集合を 構築する.
各部分系 system_i から, 方程式 eq を取出し, 変数 var を選択する. ここで変数 var は非零で最小次数を 持つものから選ぶ. それから方程式 eq と部分系 system_i - eq に含まれる方程式 eq_j を変数 var の多項式 と看倣して終結式を計算する. この操作によって, 新しい部分系 system_(i+1) がより少ない変数で生成される. それから (1) の処理に戻る.
一つの方程式で構成される部分系が最終的に得られると, その方程式が多変数で, 浮動小数による近似が なければ, 厳密解を求めるために solve を呼び出す. 方程式が単変数で線型, 2次, 或いは 4次の多項式で 近似されていれば, solve が再び呼出される. 近似されている場合や方程式が単変数で線型, 2次又は4次の 何れでもなく, realonly が true の場合, 実数値解を見付けるために関数 realroots を呼び出す. realonly が false の場合, 解を求めるために allroots が呼び出される. なお, algsys が要求以下の 精度解を生成した場合、algepsilon の値をより小さな値に変更してもかまわない. algexact が true であれば, solve が常に呼び出される.
- の段階で得られた解を以前の段階に挿入し, 解の計算過程は (1) に戻る.
なお, 浮動小数を近似した 多変数方程式に対しては,
次のメッセージを表示する:
”algsys cannot solve - system too complicated.” (意味:”algsys では解けません - 系が あまりにも複雑である.”)
radcan を使えば, 大きくて複雑な式ができる. この場合, pickapart や reveal を解の計算に使える. ここで, 解が完全 (exact) であれば flag の個所はない. そうでなければ, 不完全や非閉形式解に各々対応する approximate か incomolete という語になる. 級数による手法を用いると, nterms は取られた 項の数 (これは, エラーがより多くの項の生成を妨げた場合, ieqn に対して与えられた n よりも小さくなる) を与える.
- の段階で得られた解を以前の段階に挿入し, 解の計算過程は (1) に戻る.
なお, 浮動小数を近似した 多変数方程式に対しては,
次のメッセージを表示する:
● rootsconmode:true
rootscontract 命令の挙動を定める.
● solvedecomposes:true
true であれば, 多項式を解く際に, solve に polydecomp を導入する.
● solveexplicit:false
true であれば solve に陰的な解, 即ち, \(f(x)=0\) の形式で返すことを禁止する.
● solvefactors:true
false であれば, solve は式の因子分解を実行しない.
● solvenullwarn:true
true であれば, 空の方程式リストや空の変数リストで solve
を呼んだ場合に警告が出る. 例えば, solve([], []); と入力すると警告と []
が返される.
● solveradcan:false
true であれば solve は radcan を用いる. radcan を使うと solve
は遅くなるが, 指数や対数関数を含む 問題に対処できる.
● solvetrigwarn:true
false であれば, solve は方程式を解くために逆三角関数を利用し,
それによって解が失なわれることを 警告しない.
● solve_inconsistent_error:true
true であれば, solve と linsolve は, [a+b=1, a+b=2]
の様に階数が不十分な線形連立方程式に遭遇すれと エラーを表示する. false
であれば, 空リスト [] を返す.
17.3 代数方程式に関連する関数
● algsys([eq_1, eq_2, …], [var_1, var_2, …])
algsys は多項式方程式のリストや連立多項式方程式を,
与えられた変数リストに対して解く. 返却される解に %r1 や %r2
といった記号が含まれることがある.
これらは助変数を表示するために用いられる もので, 助変数は環境変数
%rnum_list に追加される.
/home/inoue/bin/go tmp_lang/chunk-153.mx > tmp_lang/chunk-153.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-153.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-153.mx
algsys([2*x+3*y = 1],[x,y])
2 %r1 - 1
[[x = %r1, y = - ---------]]
3
%rnum_list
[%r1]
/var/www/html/LANG/tmp_lang/chunk-153.mxこの例の様に, (連立)方程式の階数が足りない場合には,
助変数を補って与えられた方程式を解く. なお, %rnum_list には algsys
で使われた助変数が逐次追加されて行く.
algsys は以下の手順で方程式を解き,
必要であれば再帰的に処理をおこなう.
- first 解を見付ける第一の方法を試みる.
- all 全ての適応可能な方法を試みる.
実数値解であるにもかかわらず, 解の中に純虚数 %i が入っていることがある.
● allroots(eq)
単変数の実数係数多項式に対して実数解と複素解全てを計算する. 実多項式には
Jenkins(Algorithm 493,toms,vol. 1, (1975),p.178), 複素多項式には,
Jenkins と Traub のアルゴリズム (Algorithm
419,comm. acm,vol.15,(1972), p. 97) が用いられている. polyfactor が true
のとき, 与えられた 多項式が実係数であれば実数上で因子分解をおこなうが,
係数に %I が含まれていれば複素数上で因子分解を おこなう.
/home/inoue/bin/go tmp_lang/chunk-154.mx > tmp_lang/chunk-154.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-154.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-154.mx
allroots(%i*x^2+1 = 0)
[x = 0.7071067811865476 %i + 0.7071067811865475,
x = (- 0.7071067811865476 %i) - 0.7071067811865475]
polyfactor:true
allroots(x^2+1 = 0)
2
1.0 (x + 1.0)
allroots(%i*x^2+1 = 0)
1.0 %i (x - 0.7071067811865476 %i - 0.7071067811865475)
(x + 0.7071067811865476 %i + 0.7071067811865475)
/var/www/html/LANG/tmp_lang/chunk-154.mxallroots は重複解を持つときに不正確な結果を返すことがある. この場合は与式に %i をかけたものを計算 すれば解決する場合かもしれない. allroots は多項式方程式以外には使えない. rat 命令を実行した後に, 方程 式の分子が多項式で, 分母が高々複素数でなければならない. polyfactor が true であれば, allroots の 結果として常に同値な式 (ただし, 因子分解されたもの) が返される.
● funcsolve(eq, g(t))
方程式eqを満たす有理関数 g(t) が存在すれば有理関数のリストを返し,
存在しない場合は空リストを返す. ただし, 方程式は g(t) と g(t + 1)
の1次線形多項式でなければならない. 即ち, funcsolve は1次線形結合の
漸化式に対して利用できる. ただし, この関数の出来はまだ良くない.
/home/inoue/bin/go tmp_lang/chunk-155.mx > tmp_lang/chunk-155.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-155.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-155.mx
funcsolve((n+1)*foo(n)-((n+3)*foo(n+1))/(n+1) = (n-1)/(n+2),foo(n))
solve: dependent equations eliminated: (4 3)
n
foo(n) = ---------------
(n + 1) (n + 2)
/var/www/html/LANG/tmp_lang/chunk-155.mx● ieqn(eq, unknown_func, method, n , guess)
積分方程式eqを解く関数である. なお, この関数は保存領域の解放を行うため,
kill(labels) が含まれています. kill(labels) を実行すると, 入力 (%i
ラベルに保存) や計算結果 (%o ラベルに保存) は全て失われてしまう.
そのため, 積分方程式パッケージを読込む前に,
保持しておきたい式に名前を付けておかなければならない. ここで,
第3引数の手法には, 以下の2種類がある.
| 式 | rootsconmode | rootscontract の結果 |
|---|---|---|
| x^(1/2)*y^(3/2) | false | 1/2) |
| x^(1/2)*y^(1/4) | false | x^(1/2)*y^(1/4) |
| x^(1/2)*y^(1/4) | true | (x*y(1/2))(1/2) |
| x^(1/2)*y^(1/3) | true | x(1/2)*y^(1/3) |
| x^(1/2)*y^(1/4) | all | (x^2*y)^(1/4) |
| x^(1/2)*y^(1/3) | all | 1/6) |
第4,第5引数の n と guess は neumann や rstkindseries への予測値の初期値になる. n は taylor, neumann, rstkindseries や fedseries (微分手法に対する繰返しの最大深度でもある) から 取る羃の最大次数である. 第二から第五の助変数に対する初期値は, unk:p(x) である. ここで p は第一の関数で, Maxima の未知関数となる被積分関数に現れる. そして, x は第2種の方程式の場合, 積分の外側で現われる. p の第一の出現に対応する引数として現われるか, 第 1 種の方程式で積分変数を除いたその他の変数となる. x を探すことに失敗すると, 利用者は独立変数を与えることを要求される. tech:first; n: 1; guess:none これで neumann と rstkindseries を初期予測値として \(f(x)\) を用いる.
● lhs(eq)
● rhs(eq)
lhs は方程式eqの演算子=の左側を返し, rhs は右側の式を返す.
● linsolve([eq_1, eq_2, …], [var_1, var2, …])
与えられた線形連立方程式を変数リストに対して解く.
各方程式は各々与えられた変数リストの多項式でなければ ならないが,
方程式であっても構わない. なお, globalsolve が true であれば, solve
で解かれた変数に 連立方程式の集合の解が設定される.
/home/inoue/bin/go tmp_lang/chunk-156.mx > tmp_lang/chunk-156.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-156.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-156.mx
d1:x+z = y
d2:2*a*x-y = 2*a^2
d3:y-2*z = 2
ev(linsolve([d1,d2,d3],[x,y,z]),globalsolve:true)
[x : a + 1, y : 2 a, z : a - 1]
/var/www/html/LANG/tmp_lang/chunk-156.mx● nroots(poly, low, high)
上限hightと下限lowで指定された半開区間 (下限, 上限]
内部に存在する単変数多項式poly の実数根の個数を 返す.
区間の終点は負の無限大と正の無限大に各々対応する minf, inf
でもかまわない. アルゴリズムには Sturm
級数による手法が適用されている.
/home/inoue/bin/go tmp_lang/chunk-157.mx > tmp_lang/chunk-157.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-157.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-157.mx
nroots(x^2+2,-2,2)
0
nroots(x^2-2,-2,2)
2
nroots(x^2-5,-2,2)
0
nroots(x^2-1,-2,2)
2
/var/www/html/LANG/tmp_lang/chunk-157.mx● nthroot(poly, n)
多項式polyは整数係数の多項式, n を正整数, 返すのは整数上の多項式で,
この多項式の n 乗が多項式となるか, そうで無ければ多項式が完全な第 n
の羃乗ではないというエラーメッセージが表示される. このルーチンは factor
や sqfr よりも遥かに速い特徴を持っている.
/home/inoue/bin/go tmp_lang/chunk-158.mx > tmp_lang/chunk-158.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-158.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-158.mx
nthroot(x^2+2*x+1,2)
x + 1
print("nthroot(x^3+3*x^2+3*x+1,2); ---> Not an nth power")
nthroot(x^3+3*x^2+3*x+1,2); ---> Not an nth power
nthroot(1-3*x+3*x^2-x^3,3)
1 - x
/var/www/html/LANG/tmp_lang/chunk-158.mx● realroots(poly)
● realroots(poly, bound)
多項式polyは実単変数多項式で,
その全ての実根を許容範囲boundで指定する許容範囲内で求める. ここで,
許容範囲が 1 よりも小さければ, 全ての整数根を厳密に求める.
許容範囲は希望する精度を達成するために
任意の小さな数を設定してもかまわない. 許容範囲を省略した場合は,
rootsepsilon に設定した値が使われる. realroots は解の重複度リスト
multiplicities を設定する.
/home/inoue/bin/go tmp_lang/chunk-159.mx > tmp_lang/chunk-159.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-159.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-159.mx
realroots(x^2-2 = 0,1.0E-5)
370727 370727
[x = - ------, x = ------]
262144 262144
float(sqrt(2)-rhs(%o34[2]))
1.414213562373095
/var/www/html/LANG/tmp_lang/chunk-159.mxこの例では多項式ではなく, 方程式 \(x-2 - 2 = 0\) を精度 1.0e-5 以内で求めている. 解は浮動小数点 ではなく, 有理数の形で返される.
● rootscontract(exp)
式expを有理数次数の羃同士の積を環境変数 rootsmode の値に従ってまとめる.
例えば, rootsmode が true の場合, x(1/2)y^(3/2)
の様な根同士の積を sqrt(xy3) の様にまとめたものに変換する.
rootsconmode が false ならば, rootscontract は wrt
有理数次数の分母が同じ次数の羃だけを まとめる. true の場合,
次数の分母が割切れる羃だけをまとめる.all の場合, 全ての有理次数の分母の
LCM を取ってまとめる.
式 exp が変数 var のの線形結合であれば, var に対して自明に解ける.
式 exp が a var^n + b の形式ならば, 解は (-b/a)^(1/n) に 1 の n 乗根を掛けたもので得られる.
式 exp が変数 var の線形結合ではなく, 式 exp に含まれる var の各次数の gcd (n とする) が 次数を割切る場合には, 根の重複度リスト multiplicities に n が追加される. そして, solve は var^n で exp を割った結果に対して再び呼出される.
exp が因子分解されている場合, 各因子に対して solve が呼出される.
式 exp が2次, 3次, 又は4次の多項式方程式の場合, 解の公式を必要があれば用いる.
radexpand が true で domain が real であれば, rootscontract は abs を sqrt に変換する. 即ち, abs(x)sqrt(y) を sqrt(x^2y) に変換する. rootscontract は logcontract と似た手法で ratsimp を用いる.
● solve(eq)
● solve(eq, var)
● solve([eq_1, … , eq_n])
● solve([eq_1, … , eq_n], [var_1, … , var_n])
代数方程式を変数に対して解き, 方程式の解のリストを返す.
式が方程式でなければ, 式が零に等しいと仮定する. 即ち, 式 \(x^2+2*x+1\) が式であれば, solve は方程式
\(x^2+2*x+1=0\) が与えられたと解釈する.
変数は和や積を除く関数の様なアトムでない式でも構わない. なお, 式が関数
\(f(x)\) の多項式であれば, 最初に \(f(x)\) に対して解き, その結果を \(c\) とすれば, 方程式 \(f(x)=c\) を解くことで対処出来る.
/home/inoue/bin/go tmp_lang/chunk-160.mx > tmp_lang/chunk-160.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-160.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-160.mx
d1:solve(log(x)^2-2*log(x)+1,log(x))
[log(x) = 1]
solve(d1[1],x)
[x = %e]
/var/www/html/LANG/tmp_lang/chunk-160.mx式が1変数のみの場合は変数を省略できる. 更に, 式は有理式でも良く, その上, 三角関数, 指数関数等を 含んでいてもかまわない. solve は与えられた方程式が単変数の場合は次の手順で解の計算をおこなう.
'diff(f,x,2)=sin(x)+'diff(g,x);
'diff(f,x)+x^2-f=2*'diff(g,x,2); solve([eq_1, … , eq_n], [var_1, … , var_n]) の場合, 多項式の方程式系を linsolve, 或いは algsys を用いて解き, その変数で解のリストを返す. linsolve を用いる場合, 第一引数のリスト (eq_i, i=1, … , n) は解くべき方程式を表現し, 第二の引数リストは求めるべき未知変数のリストになるが, 方程式中の変数の総数が方程式数と等しい場合, 第二の引数リストは省略してもかまわない. 与えられた方程式が 十分でない場合, inconsistent と云うメッセージを表示する. これは環境変数 solve_inconsistent_error で 制御できる. 単一解が存在しない場合は singular と表示される.
18 微分方程式
Maxima での微分方程式の記述は通常の方程式と同様に, 演算子 = を挟んで左右に式が記述される形となるが, 式中に名詞型の微分 ’diff が含まれている. 更に, 未知関数がどの様な変数に依存するものかを明示的に 記述しなければならない. 例えば, 次の書式は正確な書式ではない. 何故なら, f と g が何の変数であるか 判らない.
'diff(f,x,2)=sin(x)+'diff(g,x);
'diff(f,x)+x^2-f=2*'diff(g,x,2); 'diff(f(x),x,2)=sin(x)+’diff(g(x),x);
’diff(f(x),x)+x^2-f(x)=2*’diff(g(x),x,2);常微分方程式に初期値を与えたければ, 普通の関数と同様に atvalue
命令を用いる. なお, atvalue で 初期値を設定する場合は, desolve や ode
を用いて微分方程式を処理する前に初期値の設定を行わなければ ならない.
atvalue は atvalue(f(x),x = pt,val) で, 関数 f(x) に対し, x=pt で値 val
を設定する. なお, f が多変数の場合は
atvalue(f(x,y,…),[x1=p1,x2=p2,…],[val1,val2,…])
の様に境界と対応する値をリストで与える.
◆ 実行例: \[ x^2\,y' + 3\,x\,y = \frac{\sin x}{x} ~ \rightarrow ~ y' + \frac{3}{x} \,y = \frac{\sin x}{x^3} ~ \rightarrow ~ y' + P(x)\,y = Q(x) \]
/home/inoue/bin/go tmp_lang/chunk-161.mx > tmp_lang/chunk-161.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-161.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-161.mx
d1:x^2*'diff(y,x)+3*y*x = sin(x)/x
d2:ode2(d1,y,x)
%c - cos(x)
y = -----------
3
x
"/* 注:初期条件 x=%pi,y=0 の下で解く */"
ic1(d2,x = %pi,y = 0)
cos(x) + 1
y = - ----------
3
x
/var/www/html/LANG/tmp_lang/chunk-161.mx◆ 実行例:\(y'' + y\,(y')^3 = 0\)
/home/inoue/bin/go tmp_lang/chunk-162.mx > tmp_lang/chunk-162.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-162.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-162.mx
d2:'diff(y,x,2)+y*('diff(y,x))^3 = 0
d3:ode2(d2,y,x)
3
y + 6 %k1 y
------------ = x + %k2
6
ratsimp(ic2(d3,x = 0,y = 0,'diff(y,x) = 2))
3
y + 3 y
-------- = x
6
bc2(d3,x = 0,y = 1,x = 1,y = 3)
3
y - 10 y 3
--------- = x - -
6 2
/var/www/html/LANG/tmp_lang/chunk-162.mx18.1 微分方程式に関連する関数
● bc2(solution, xvalue_1, yvalue_1, xvalue_2, yvalue_2)
2階の微分方程式の境界条件問題を解く. ここで一般解solution は, ode2
等で計算した微分方程式の 一般解である.
2階の方程式の一般解では定数が二つ現われるため, 特殊解を求めるため,
異なった2点での 連立方程式を解く必要がある. そのため, xvalue_1 と
yvalue_1 が一つの点での値, xvalue_2 と yvalue_2
がもう一つの別の点での値を定める. ここで, 値の与え方は, 一般解の変数を x
と y とすると, xvalue_1 と yvaue_1 を x=x0 や y=y0 の様に,
<対応する変数> = <境界値> の書式で記述する. なお, load(ode2)
でプログラムの読込を行う必要がある.
● desolve([eq_1,… , eq_n],[var_1,… , var_n])
微分方程式 eq_i とその従属変数 var_1,… var_n を指定する. ここで,
関数と変数の関連性ははっきと 指定しなければならない. 又, 初期条件は
desolve を呼出す前に, altvalue 関数で与えなければならない.
解はリストの形式で返却されるが, 解を得られなかった場合, desolve は false
を返す. なお, load(ode2) でプログラムの読込を行う必要がある.
◆ 実行例:
/home/inoue/bin/go tmp_lang/chunk-163.mx > tmp_lang/chunk-163.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-163.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-163.mx
d1:'diff(f(x),x) = 'diff(g(x),x)+sin(x)
d2:'diff(g(x),x,2) = 'diff(f(x),x)-cos(x)
atvalue('diff(g(x),x),x = 0,a)
a
atvalue(f(x),x = 0,1)
1
d3:desolve([d1,d2],[f(x),g(x)])
x x
[f(x) = a %e - a + 1, g(x) = cos(x) + a %e - a + g(0) - 1]
"/* 注: 検証 */"
ev([d1,d2],d3,diff)
x x x x
[a %e = a %e , a %e - cos(x) = a %e - cos(x)]
/var/www/html/LANG/tmp_lang/chunk-163.mx● ic1(solution, xvalue, yvalue)
初期値問題 (ivp) と境界値問題 (bvp) を解くための ode2
パッケージに含まれるプログラムである. solution は ode
等で計算した微分方程式の一般解となる. 後の二つが境界条件を与える.
一般解の変数を x, y とすると, xvalue と yvalue は x=x0 や y=y0 の様に,
<対応する変数> = <境界値> の書式になる. なお, load(ode2)
でプログラムの読込を行う必要がある.
● ic2(solution, xvalue, yvalue)
1階の微分方程式の境界値問題を解く関数である.solution は ode
等で計算した微分方程式の一般解となり, 後の二つがその境界条件を与える.
一般解の変数を x, y とすると, xvalue と yvalue は x=x0 や y=y0 の様に,
<対応する変数> = <境界値> の書式になる. なお, load(ode2)
でプログラムの読込を行う必要が ある.
● ode2(eq, dependent_var, independent_var)
3 個の引数を取る. 最初の eq は1階, 又は2階の常微分方程式を与える. なお,
常微分方程式の右側 (rhs(exp)) が 0 ならば,
左側のみを与えるだけでもかまわない. 第二引数dependent_varは従属変数,
最後の引数 independent_varが独立変数となる. 求解に成功すると,
従属変数に対する陽的な解, 或いは陰的な解の何れかを 返す. ここで, %c
は1階の方程式の定数, %k1 と %k2
は2階の方程式の定数を表記するために用いられる. ode2
が何らかの理由で解が得られなかった場合, エラーメッセージの表示等の後に
false を返す. 現在, 1階常微分方程式向けに実装され, 検証されている解法は,
線型, 分離法, 厳密 (積分因子が多分要求される), 同次, bernoulli 方程式,
そして一般化同次法がある. 2階の常微分方程式に対しては, 定数係数, 厳密,
定数係数に変換可能な非定数係数を持つ線型同次方程式, Euler
又は同次元方程式, 仮想変位法, そして
変形分離で解ける二つの独立な1階の線型な方程式に縮約可能となる方程式を含まないものがある.
常微分方程式を解く手順では, 幾つかの変数は純粋に情報的な目的, method
が記述する解法の集合である. 例えば, linear, intfactor
が記述する積分因子を用い, odeindex は Bernoulli 法や一般化同次法の
添字を記述し, yp は仮想変位による特殊な解法を記述している.
18.2 補足
\(y=y(x)\) の導関数 \(y' = \dfrac{dy}{dx},\, y'' = \dfrac{d^2 y}{dx^2},\, \cdots\) および,\(x\) の関数を含む方程式を「微分方程式」という.
\[\begin{array}{lll} (a)~y'=x-3, & (b)~y' + 2y = e^x & \cdots 1階の微分方程式 \\ (c)~y'' + 3 y' + 2y = 0, & (d)~(y'')^2 + y' + 3y = e^x &\cdots 2階の微分方程式 \end{array}\] \[\begin{array}{l} 上記の微分方程式を満たす関数 y=y(x) を「微分方程式の解」という. \rightarrow 解は関数として求まる(関数方程式の1つ). \end{array}\] 微分方程式の構成\[\begin{array}{l} (例)~ x^2 + y^2 - c x = 0 \quad (c : 任意定数) \quad \cdots (1)\\ (1) から任意定数 c を消去して微分方程式を構成する.\\ \qquad \dfrac{d}{dx}~:~ 2x + 2yy' - c = 0 \qquad \rightarrow \quad c = 2 (x+yy') \\ \qquad \rightarrow \quad x^2 + y^2 - 2 (x+yy')x = 0 \\ \qquad 2xy y' + x^2 - y^2 = 0 \quad (微分方程式) \end{array}\] 微分方程式の解(一般解,特殊解,特異解)
\[\begin{array}{l} (例)~ 微分方程式 ~:~ (y')^3 = 27\,y^2 ~の解\\ \qquad 一般解: y= (x+c)^3 \quad (c : 任意定数)\\ \qquad 特殊解: y= (x+1)^3 \\ \qquad 特異解: y= 0 \quad (一般解ではカバーできない解)\\ \qquad 初期条件 「x=a のとき y=b」 の下で微分方程式を解く \end{array}\]
変数分離形
\[\begin{array}{l} \dfrac{dy}{dx} = f(x)g(y) \rightarrow \int \frac{1}{g(y)} dy = \int f(x)dx + c \end{array}\]◆ 実行例: \(y' = k\,y, \quad y' = 2\,x\,y\)
/home/inoue/bin/go tmp_lang/chunk-164.mx > tmp_lang/chunk-164.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-164.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-164.mx
eq1:diff(y(x),x) = k*y(x)
ode2(eq1,y(x),x)
k x
y(x) = %c %e
eq2:diff(y(x),x) = 2*x*y(x)
ode2(eq2,y(x),x)
2
x
y(x) = %c %e
/var/www/html/LANG/tmp_lang/chunk-164.mx変数分離形へ
\[\begin{array}{l} \dfrac{dy}{dx} = f(ax+by+c) \\ \rightarrow u = ax +by +c \rightarrow u' = a + by' \rightarrow y' = \dfrac{u'-a}{b} = f(u) \\ \rightarrow u' = \dfrac{du}{dx} = a + b\,f(u) \quad \rightarrow \int \,\dfrac{1}{a+ b\,f(u)} \,du = \int 1\, dx + c \end{array}\]◆ 実行例: \(y\,y' + x = 0\)
/home/inoue/bin/go tmp_lang/chunk-165.mx > tmp_lang/chunk-165.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-165.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-165.mx
eq3:y(x)*diff(y(x),x)+x = 0
ode2(eq3,y(x),x)
2 2
y (x) x
- ----- = -- + %c
2 2
/var/www/html/LANG/tmp_lang/chunk-165.mx同次形
\[\begin{array}{l} \dfrac{dy}{dx} = f\left(\dfrac{y}{x}\right) \\ u = \dfrac{y}{x} \rightarrow y = x\,u \quad \rightarrow \quad y' = u + x\,u' \\ y' = f(u) \rightarrow u' = \dfrac{f(u)-u}{x} \\ \rightarrow \displaystyle\int \dfrac{1}{f(u)-u} du = \int \dfrac{1}{x} dx + c \\ \end{array}\]◆ 実行例: \(3\,x\,y^2\, y' = x^3 + y^3\)
/home/inoue/bin/go tmp_lang/chunk-166.mx > tmp_lang/chunk-166.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-166.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-166.mx
eq4:3*x*y(x)^2*diff(y(x),x) = x^3+y(x)^3
ode2(eq4,y(x),x)
3 3
2 y (x) - x
------------ = %c
2 x
/var/www/html/LANG/tmp_lang/chunk-166.mx1階線形微分方程式
\[\begin{array}{l} \fbox{$ \dfrac{dy}{dx} + P(x)y = Q(x) \quad \Rightarrow \quad y = e^{-\int Pdx} \left( \int Q(x)\,e^{\int Pdx} dx + c \right) $ } \\ \dfrac{dy}{dx} + P(x)\,y = 0 を解く \rightarrow \dfrac{1}{y}\, dy = -P(x)\, dx \rightarrow \log y = -\int P(x) dx + c \\ y = c e^{-\int Pdx} \quad (定数変化法:~c = u(x)) \quad \rightarrow y = u(x) e^{-\int Pdx} \quad (この式を微分し与式と比較) \\ y' = u' e^{-\int Pdx} + u (-P(x))e^{-\int Pdx} = u' e^{-\int Pdx} - P(x)y \quad \leftrightarrow \quad y' = Q(x) - P(x)y \\ u' e^{-\int Pdx} = Q(x) \rightarrow \dfrac{du}{dx} = Q(x) \,e^{\int Pdx} \rightarrow u = \int Q(x)\,e^{\int Pdx} dx + c \\ \end{array}\]例1(1): \(\displaystyle\dfrac{dy}{dx} + \dfrac{1}{x}\,y = 1-x^2\)
\[\begin{array}{l} P = \dfrac{1}{x}, \quad Q = 1-x^2 \\ \displaystyle \int P dx = \displaystyle \int\dfrac{1}{x} \,dx = \log x \rightarrow e^{\int P dx} = e^{\log x } = x, \quad e^{-\int P dx} = e^{-\log x } = \dfrac{1}{x} \\ \displaystyle \int Q\,e^{\int P dx}\,dx = \displaystyle \int(1-x^2)\,x\,dx = \dfrac{1}{2}x^2 - \dfrac{1}{4}x^4 + c \\ y = e^{-\int Pdx} \left( \int Q(x)\,e^{\int Pdx} dx + c \right) = \dfrac{1}{x}\,\left( \dfrac{1}{2}x^2 - \dfrac{1}{4}x^4 + c \right) \\ \quad = \dfrac{1}{2}x - \dfrac{1}{4}x^3 + \dfrac{c}{x} \end{array}\]◆ 実行例: \(\displaystyle\frac{dy}{dx} + \frac{1}{x}\,y = 1 - x^2\)
/home/inoue/bin/go tmp_lang/chunk-167.mx > tmp_lang/chunk-167.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-167.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-167.mx
eq5:diff(y(x),x)+(1/x)*y(x) = 1-x^2
d1:ode2(eq5,y(x),x)
2 2
(1 - x )
%c - ---------
4
y(x) = --------------
x
/var/www/html/LANG/tmp_lang/chunk-167.mx完全微分形1
\[\begin{array}{l} \hspace{-2ex} P(x,y)dx + Q(x,y)dy = 0 \quad \Leftrightarrow \quad c = \displaystyle \int P(x,y)dx + \displaystyle \int\left( Q(x,y) - \frac{\partial}{\partial y} \displaystyle \int P(x,y)dx \right)dy \\ \end{array}\]\[ \begin{array}{ll} 予備知識 & \\ & u=u(x,\,y),~y=y(x)~の全微分\\ & \displaystyle \frac{du}{dx} = \frac{\partial u}{\partial x}\,\frac{dx}{dx} + \frac{\partial u}{\partial y}\,\frac{dy}{dx} = u_{x} \,\frac{dx}{dx} + u_{y} \,\frac{dy}{dx} \\ & du = u_{x} \,dx + u_{y} \, dy \\ \end{array} \]
\[ \displaystyle \begin{array}{l} u=u(x,y) を考え,その全微分に着目する.\\ \left\{ \matrix{ du &=& u_x dx + u_y dy = P(x,y)dx + Q(x,y)dy \cr du &=& 0 \quad \rightarrow u = c } \right. \\ 完全微分形の条件:~ u_{xy} = u_{yx} \quad \Leftrightarrow \quad \frac{\partial}{\partial y} P = \frac{\partial}{\partial x} Q \\ u_x = \frac{\partial u}{\partial x} = P(x,y) \rightarrow u = \int P(x,y) dx + \phi(y) \quad (yを固定した積分)\quad \cdots\cdots (1)\\ \rightarrow \frac{\partial }{\partial y}u = \frac{\partial}{\partial y} \left\{ \int P(x,y)dx +\phi(y) \right\} = Q(x,y)\\ \rightarrow \phi'(y) = Q(x,y) - \frac{\partial}{\partial y}\int P(x,y)dx \qquad (\phi'(y)~は~y~ のみの関数となる:注)\\ \rightarrow \phi(y) = \int \left\{Q(x,y) - \frac{\partial}{\partial y}\int P(x,y)dx \right\}dy \quad\cdots\cdots(2) \quad (これを(1)に代入) \end{array} \]
\[ \begin{array}{l} 注~:~ 「u = u(x,y)~ が 完全微分形~:~u_{xy} = u_{yx} ~\Leftrightarrow~ P_y = Q_x~であれば~ \\ \quad\phi'(y) = Q(x,y) - \frac{\partial}{\partial y}\int P(x,y)dx ~ ~は~y~ のみの関数となる.」(以下に示す)\\ f = Q(x,y) - \frac{\partial}{\partial y}\int P(x,y)dx ~として,~f_x = 0~ を示 せば,~f~は~y~ のみの関数となる.\\ 完全微分形の条件より,~\dfrac{\partial}{\partial y}\displaystyle \int P dx = \displaystyle \int\dfrac{\partial}{\partial y} P dx = \displaystyle \int Q_x \,dx = Q \\ f_x = \dfrac{\partial f}{\partial x} = Q_x - \dfrac{\partial }{\partial x} \left( \frac{\partial}{\partial y}\displaystyle \int P\,dx \right) = Q_x - \dfrac{\partial }{\partial x} Q = Q_x - Q_x = 0 \end{array} \]
例1:~微分方程式 \(\displaystyle(3x^2+3y)dx + (3x+y-1)dy =0\)~ が完全微分形であることを示し, その一般解を求めよ.
\[ \begin{array}{lll} u_{x} = P = 3x^2+3y & \rightarrow & u_{xy} = P_{y} = 3 \\ u_{y} = Q = 3x+y-1 & \rightarrow & u_{yx} = Q_{x} = 3 \\ \end{array} \]
\(u_{xy} = u_{yx}\) より,完全微分形である.
\[ \begin{array}{l} u_{x} = P = 3x^2+3y ~\rightarrow~ u = \displaystyle \int P \,dx + \phi(y) = x^3 + 3xy + \phi(y) \quad \cdots\cdots (1)\\ 上式を y で偏微分すると,~u_{y} = 3x + \phi'(y) \\ 上式と ~ u_{y} = Q = 3x+y-1 ~ から~ \phi'(y) = y-1 \quad \rightarrow \quad \phi(y) = \displaystyle \int(y-1) dy = \dfrac{1}{2}y^2 - y\\ (1)より,u = x^3 + 3xy + \dfrac{1}{2}y^2 - y\\ 求める一般解は ~u=c~,すなわち,~ x^3 + 3xy + \dfrac{1}{2}y^2 - y = c \end{array} \]
\[ \begin{array}{l} (別解)\\ u_{x} = 3x^2+3y \rightarrow u = \displaystyle \int u_{x}dx = x^3 + 3xy + \phi(y)\\ u_{y} = 3x+y-1 \rightarrow u = \displaystyle \int u_{y}dy = 3xy + \dfrac{1}{2}y^2 - y +\psi(x) \\ \phi(y) = \dfrac{1}{2}y^2 - y, \quad \psi(x) = x^3 ~と見なせば,\\ u = x^3 + 3xy + \dfrac{1}{2}y^2 - y = c \end{array} \]
◆ 実行例: \(\displaystyle(3x^2+3y)dx + (3x+y-1)dy =0\)
/home/inoue/bin/go tmp_lang/chunk-168.mx > tmp_lang/chunk-168.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-168.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-168.mx
ux:3*x^2+3*y(x)
uy:3*x+y(x)-1
eq6:ux+uy*diff(y(x),x) = 0
ode2(eq6,y(x),x)
2 3
y (x) + (6 x - 2) y(x) + 2 x
----------------------------- = %c
2
/var/www/html/LANG/tmp_lang/chunk-168.mx完全微分形2
\[ \begin{array}{l} \hspace{-2em} 微分方程式~ P(x,y)dx + Q(x,y)dy = 0 ~が 完全微分形~:~u_{xy} = u_{yx} ~\Leftrightarrow~ P_y = Q_x~であれば,\\ その一般解は次式で表せる. \\ \qquad \displaystyle \int_{x_0}^{x} P(x,y)dx + \displaystyle \int_{y_0}^{y} Q(x_0,y)dy = c \quad (ただし,x_0, \, y_0 は定数) \\ また,初期条件~:~「x =x_0,~y=y_0」~の下での特殊解は次式で表せる.\\ \qquad \displaystyle \int_{x_0}^{x} P(x,y)dx + \displaystyle \int_{y_0}^{y} Q(x_0,y)dy = 0 \end{array} \]
\[ \begin{array}{l} 以下に示す.\\ u = u(x,y) = \displaystyle \int_{x_0}^{x} P(x,y)dx + \displaystyle \int_{y_0}^{y} Q(x_0,y)dy ~とおく.\\ 上式が完全微分形の条件~:~u_{xy} = u_{yx} ~\Leftrightarrow~ P_y = Q_x~の下で, 微分方程式~\\P(x,y)dx + Q(x,y)dy = 0 をみたすことを示す.\\ u_x = \dfrac{\partial u}{\partial x} = P(x,y) \quad \cdots (1) \\ u_y = \dfrac{\partial u}{\partial y} = \dfrac{\partial }{\partial y} \left( \displaystyle \int_{x_0}^{x} P(x,y)dx + \displaystyle \int_{y_0}^{y} Q(x_0,y)dy \right) = \displaystyle \int_{x_0}^{x} \dfrac{\partial }{\partial y} P(x,y)dx + \dfrac{\partial }{\partial y} \displaystyle \int_{y_0}^{y} Q(x_0,y)dy \\ \quad \quad \leftarrow \dfrac{\partial }{\partial y} P(x,y) = P_y(x,y) = Q_x(x,y) \quad (完全微分形の条件より)\\ \quad = \displaystyle \int_{x_0}^{x} Q_x(x,y)\,dx + Q(x_0,y) = \left[ Q(x,y)\right]_{x=x_0}^{x} + Q(x_0,y) = Q(x,y) - Q(x_0,y) + Q(x_0,y) \\ \quad = Q(x,y) \quad \cdots (2) \\ (1), (2) より,~u = u(x,y)~は微分方程式~P(x,y)dx + Q(x,y)dy = 0~を満たす. \\ \end{array} \]
例2 \[ \begin{array}{ll} (1)&(y^2e^{xy^2} + 4x^3)dx + (2xye^{xy^2} - 3y^2)dy = 0 ~(完全微分形)~を解く. \\ (2)&初期条件「x=1,~y=0」の下で,(1)を解く. \end{array} \]
\[ \begin{array}{l} u_{x} = P = y^2e^{xy^2} + 4x^3 ~\rightarrow~ u_{xy} = P_y = (2y+2xy^3)e^{xy^2}\\ u_{y} = Q = 2xye^{xy^2} - 3y^2 ~\rightarrow~ u_{yx} = Q_x = (2y+2xy^3)e^{xy^2}\\ x_0 = 0,~y_0 = 0~(計算が楽)として,公式を計算する\\ \displaystyle \int_{x_0}^{x} P(x,y)dx = \displaystyle \int_{0}^{x} (y^2e^{xy^2} + 4x^3)dx = \left[ e^{xy^2} + x^4 \right]_{x=0}^{x} = e^{xy^2} + x^4 \\ \displaystyle \int_{y_0}^{y} Q(x_0,y)dy = \displaystyle \int_{0}^{y} Q(0,y)dy = \displaystyle \int_{0}^{y} (-3y^2)dy = \left[ -y^3 \right]_{y=0}^{y} = -y^3 \\ u = e^{xy^2} + x^4 -y^3 = c ~ が(1)の解\\ (2) の解を求める.\\ \displaystyle \int_{x_0}^{x} P(x,y)dx = \displaystyle \int_{1}^{x} (y^2e^{xy^2} + 4x^3)dx = \left[ e^{xy^2} + x^4 \right]_{x=1}^{x} = (e^{xy^2} + x^4) - (e^{y^2} + 1) \\ \displaystyle \int_{y_0}^{y} Q(x_0,y)dy = \displaystyle \int_{0}^{y} Q(1,y)dy = \displaystyle \int_{0}^{y} (2ye^{y^2} - 3y^2)dy = \left[ e^{y^2} - y^3 \right]_{y=0}^{y} = (e^{y^2} - y^3 )-(1) \\ u = \left\{(e^{xy^2} + x^4) - (e^{y^2} + 1)\right\} + \left\{ (e^{y^2} - y^3 )-(1) \right\} = e^{xy^2} + x^4 - y^3 -2 = 0 \end{array} \]
◆ 実行例: \(\displaystyle(y^2e^{xy^2} + 4x^3)dx + (2xye^{xy^2} - 3y^2)dy = 0\)
/home/inoue/bin/go tmp_lang/chunk-169.mx > tmp_lang/chunk-169.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-169.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-169.mx
ux:y(x)^2*%e^(x*y(x)^2)+4*x^3
uy:2*x*y(x)*%e^(x*y(x)^2)-3*y(x)^2
eq7:ux+uy*diff(y(x),x) = 0
out:ode2(eq7,y(x),x)
2
3 x y (x) 4
(- y (x)) + %e + x = %c
ic1(out,x = 1,y(1) = 0)
2 2
3 x y (x) 4 3 y (1)
(- y (x)) + %e + x = (- y (1)) + %e + 1
/var/www/html/LANG/tmp_lang/chunk-169.mx定数係数をもつ2階線形微分方程式
\[ \begin{array}{l} \left\{ \matrix{ 同次形 : && y'' + a y' + b y &=& 0 \cr 非同次形: && y'' + a y' + b y &=& F(x) } \right. \end{array} \]
◎~ 微分方程式 \(y'' + a y' + b y = 0\) (同次形)の一般解は以下で表せる.\ 1次独立な解 \(y_1 = y_1(x), \, y_2 = y_2(x)\) が存在すれば,\ 一般解は, \(y = c_1 y_1(x) + c_2 y_2(x) \quad (c_1,\, c_2 は任意定数)\) で表せる.\
\[ \begin{array}{l} y'' + a y' + b y = 0 \quad \rightarrow \quad \lambda^2 + a \lambda + b = 0 \quad(補助方程式) \\ 補助方程式が異なる実数解:~ \lambda_1,\, \lambda_2 をもつとき,\\ 微分方程式の解は次式で表せる.\\ \quad y_1 = e^{\lambda_1 x}, \quad y_2 = e^{\lambda_2 x} \quad \rightarrow \quad y= c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} \\ \end{array} \]
\[ \begin{array}{l} y_1 = e^{\lambda_1 x} ~より~ y_1' = \lambda_1 e^{\lambda_1 x},\quad y_1'' = \lambda_1^2 e^{\lambda_1 x} \\ y_1'' + a y_1' + b y_1 = (\lambda_1^2 + a \lambda_1 + b)e^{\lambda_1 x} = 0 \times e^{\lambda_1 x} = 0 \\ よって,~y_1 = e^{\lambda_1 x}~ は~ y'' + a y' + b y = 0~ の解.\\ 同様に, ~y_2 = e^{\lambda_2 x} ~ は~ y'' + a y' + b y = 0~ の解.\\ よって,y= c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} ~ は~ y'' + a y' + b y = 0~ の解. \end{array} \]
\[ \begin{array}{l} \\ y'' + a y' + b y = 0 \quad \rightarrow \quad \lambda^2 + a \lambda + b = 0 \quad(補助方程式) \\ 補助方程式が重解:~ \lambda_1~ をもつとき,\\ 微分方程式の解は次式で表せる.\\ \quad y_1 = e^{\lambda_1 x}, \quad y_2 = x\,e^{\lambda_1 x} \quad \rightarrow \quad y= (c_1 + c_2\,x) e^{\lambda_1 x} \\ \end{array} \] \[ \begin{array}{l} y_1 = e^{\lambda_1 x} ~より~ y_1' = \lambda_1 e^{\lambda_1 x},\quad y_1'' = \lambda_1^2 e^{\lambda_1 x} \\ y_1'' + a y_1' + b y_1 = (\lambda_1^2 + a \lambda_1 + b)e^{\lambda_1 x} = 0 \times e^{\lambda_1 x} = 0 \\ よって,~y_1 = e^{\lambda_1 x}~ は~ y'' + a y' + b y = 0~ の解.\\ \end{array} \]
\[ \begin{array}{l} y_2 = x\,e^{\lambda_1 x} ~より~ \\ \quad y_2' = (x)' e^{\lambda_1 x} + x \, (e^{\lambda_1 x})' = e^{\lambda_1 x} + x \lambda_1 e^{\lambda_1 x} = (1 + x \lambda_1) e^{\lambda_1 x}\\ \quad y_2'' = (1 + x \lambda_1)' e^{\lambda_1 x} + (1 + x \lambda_1) (e^{\lambda_1 x})' \\ \quad \quad ~ = \lambda_1 e^{\lambda_1 x} + (1 + x \lambda_1) \lambda_1\,e^{\lambda_1 x} = (2\,\lambda_1 + x\,\lambda_1^2) e^{\lambda_1 x} \\ y_2'' + a y_2' + b y_2 = \displaystyle\left\{ (2\,\lambda_1 + x\,\lambda_1^2) + a(1 + x \lambda_1) + bx \right\} e^{\lambda_1 x} \\ \quad \quad ~ = \displaystyle\left\{ (\lambda_1^2 + a \lambda_1 + b)x + (2\lambda_1 + a) \right\} e^{\lambda_1 x} \\ \qquad \qquad \lambda_1^2 + a \lambda_1 + b = 0 \\ \qquad \qquad \lambda^2 + a \lambda + b = (\lambda - \lambda_1)^2 = \lambda^2 - 2\lambda_1\,\lambda + \lambda_1^2 ~ より ~ a = -2\lambda_1\\ \quad \quad ~ = 0 \\ よって~y_2 = xe^{\lambda_1 x} ~ は~ y'' + a y' + b y = 0~ の解.\\ 以上より,y= c_1 e^{\lambda_1 x} + c_2 x e^{\lambda_1 x} ~ は~ y'' + a y' + b y = 0~ の解. \end{array} \]
\[ \begin{array}{l} \\ y'' + a y' + b y = 0 \quad \rightarrow \quad \lambda^2 + a \lambda + b = 0 \quad(補助方程式) \\ 補助方程式が異なる複素数解:~ \lambda_1=\alpha+i\,\beta,\, \lambda_2=\alpha - i\,\beta を もつとき,\\ 微分方程式の解は次式で表せる.\\ \quad y_1 = e^{\lambda_1 x}, \quad y_2 = e^{\lambda_2 x} \quad \rightarrow \quad y= c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} = e^{\alpha x} \left(c_1 \cos \beta x + c_2 \sin \beta x\right)\\ \end{array} \]
\[ \begin{array}{l} オイラーの公式:~ e^{\pm ix} = \cos x \pm i \sin x \\ y = c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} = c_1 e^{\alpha x + i \beta x} + c_2 e^{\alpha x - i \beta x} = e^{\alpha x} \left( c_1 e^{i \beta x} + c_2 e^{-i \beta x}\right) \\ \quad = e^{\alpha x} \left( c_1 (\cos \beta x + i \sin \beta x) + c_2 (\cos \beta x - i \sin \beta x) \right) \\ \quad = e^{\alpha x} \left\{ ( c_1 + c_2) \cos \beta x + i (c_1 - c_2) \sin \beta x \right\} \\ \quad = e^{\alpha x} \left\{ c_1' \cos \beta x + c_2' \sin \beta x \right\} \quad (c_1' = c_1 + c_2, \quad c_2' = i (c_1 - c_2)) \end{array} \] \[ \begin{array}{l} (p.66)~ 例3(1)~ y'' - 2y' + 2y = 0 ~を解く.\\ 補助方程式:~\lambda^2 - 2\lambda + 2 = 0 \\ \quad \rightarrow \quad \lambda = 1 \pm i \quad \leftrightarrow \quad \lambda = \alpha \pm i\beta \quad(\alpha =1,\, \beta = 1)\\ y = e^{\alpha x} \left(c_1 \cos \beta x + c_2 \sin \beta x\right)\\ \quad = e^{ x} \left(c_1 \cos x + c_2 \sin x\right)\\ \end{array} \]
/home/inoue/bin/go tmp_lang/chunk-170.mx > tmp_lang/chunk-170.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-170.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-170.mx
eq8:diff(y(x),x,2)-2*diff(y(x),x)+2*y(x) = 0
ode2(eq8,y(x),x)
x
y(x) = %e (%k1 sin(x) + %k2 cos(x))
/var/www/html/LANG/tmp_lang/chunk-170.mx\[ \begin{array}{l} (p.66)~ 例4(1)~ y''' - y = 0 ~を解く.(3階の微分方程式)\\ 補助方程式:~\lambda^3 - 1 = 0 \\ \quad (\lambda -1)(\lambda^2 + \lambda + 1) = 0 \quad \rightarrow \quad \lambda = 1, \, -\,\dfrac{1}{2} \pm i \, \dfrac{\sqrt{3}}{2} \\ \quad \displaystyle y = c_1 e^{x} + c_2 e^{-\frac{1}{2}x} \cos \dfrac{\sqrt{3}}{2} x + c_3 e^{-\frac{1}{2}x} \sin \dfrac{\sqrt{3}}{2} x \end{array} \]
/home/inoue/bin/go tmp_lang/chunk-171.mx > tmp_lang/chunk-171.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-171.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-171.mx
eq9:diff(y(x),x,3)-y(x) = 0
ode2(eq9,y(x),x)
3
d
(%t3) --- (y(x)) - y(x) = 0
3
dx
not a proper differential equation
false
/var/www/html/LANG/tmp_lang/chunk-171.mx\[ \begin{array}{l} (p.66)~ 例4(2)~ y''' + 5y'' +4y'= 0 ~を解く.(3階の微分方程式)\\ 補助方程式:~\lambda^3 + 5 \lambda^2 + 4\lambda = 0 \\ \quad \lambda (\lambda + 1)(\lambda + 4) = 0 \quad \rightarrow \quad \lambda = 0, \, -1, \, -4 \\ \quad \displaystyle y = c_1 e^{0x} + c_2 e^{-1x} + c_3 e^{-4x} = c_1 + c_2 e^{-x} + c_3 e^{-4x} \end{array} \]
/home/inoue/bin/go tmp_lang/chunk-172.mx > tmp_lang/chunk-172.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-172.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-172.mx
eq10:diff(y(x),x,3)+5*diff(y(x),x,2)+4*y(x) = 0
ode2(eq10,y(x),x)
3 2
d d
(%t3) --- (y(x)) + 5 (--- (y(x))) + 4 y(x) = 0
3 2
dx dx
not a proper differential equation
false
/var/www/html/LANG/tmp_lang/chunk-172.mx\[ \begin{array}{l} (p.66)~ 例4(3)~ y''' - y'' - y' + y = 0 ~を解く.(3階の微分方程式)\\ 補助方程式:~\lambda^3 - \lambda^2 - \lambda + 1 = 0 \\ \quad (\lambda - 1)^2(\lambda + 1) = 0 \quad \rightarrow \quad \lambda = 1 ~(2重解), \, -1 \\ \quad \displaystyle y = c_1 e^{1x} + c_2 xe^{1x} + c_3 e^{-1x} = c_1 e^{x} + c_2 xe^{x} + c_3 e^{-x} \end{array} \]
/home/inoue/bin/go tmp_lang/chunk-173.mx > tmp_lang/chunk-173.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-173.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-173.mx
eq11:diff(y(x),x,3)-diff(y(x),x,2)-diff(y(x),x)+y(x) = 0
ode2(eq11,y(x),x)
3 2
d d d
(%t3) --- (y(x)) - --- (y(x)) - -- (y(x)) + y(x) = 0
3 2 dx
dx dx
not a proper differential equation
false
/var/www/html/LANG/tmp_lang/chunk-173.mx\[ \begin{array}{l} \\ \lambda^2 + a \lambda + b = 0 \quad(補助方程式) に対応して\\ (1) 異なる実数解:~ \lambda_1,\, \lambda_2 をもつとき,\\ y_1 = e^{\lambda_1 x}, \quad y_2 = e^{\lambda_2 x} \quad \rightarrow \quad y= c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} \\ (2) 重解:~ \lambda,\, をもつとき,\\ y_1 = e^{\lambda x}, \quad y_2 = x e^{\lambda x} \quad \rightarrow \quad y= (c_1 + c_2 x) e^{\lambda x} \\ (3) 複素数解:~ \lambda_1 = \alpha + i \beta,\, \lambda_2 = \alpha - i \beta をもつとき,\\ y_1 = e^{\lambda_1 x}, \quad y_2 = e^{\lambda_2 x} \quad \rightarrow \quad y = c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} = e^{\alpha x} \left(c_1 \cos \beta x + c_2 \sin \beta x\right) {1ex} \\ オイラーの公式:~ e^{\pm ix} = \cos x \pm i \sin x \\ y = c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} = c_1 e^{\alpha x + i \beta x} + c_2 e^{\alpha x - i \beta x} = e^{\alpha x} \left( c_1 e^{i \beta x} + c_2 e^{-i \beta x}\right) \\ \quad = e^{\alpha x} \left( c_1 (\cos \beta x + i \sin \beta x) + c_2 (\cos \beta x - i \sin \beta x) \right) \\ \quad = e^{\alpha x} \left\{ ( c_1 + c_2) \cos \beta x + i (c_1 - c_2) \sin \beta x \right\} \\ \quad = e^{\alpha x} \left\{ c_1' \cos \beta x + c_2' \sin \beta x \right\} \quad (c_1' = c_1 + c_2, \quad c_2' = i (c_1 - c_2)) \\ \\ \end{array} \]
非同次形
◎~ 微分方程式 \(y'' + a y' + b y = F(x)\) (非同次形)の一般解は以下で表せる.\ \(y'' + a y' + b y = 0\) (同次形)の1次独立な解(基本解)を \(y_1 = y_1(x), \, y_2 = y_2(x)\) ,\ \(y'' + a y' + b y = F(x)\) (非同次形)の特殊解を \(y_0 = y_0(x)\) とするとき, \(y'' + a y' + b y = F(x)\) (非同次形)の一般解は, \(y = y_0(x) + c_1 y_1(x) + c_2 y_2(x) \quad (c_1,\, c_2 は任意定数)\) で表せる. \ 「特殊解の求め方」 同次形の一般解: ~ \(y = c_1 y_1 + c_2 y_2\) の定数 \(c_1,c_2\) を \(c_1 = u_1(x),\, c_2 = u_2(x)\) とおく.(定数変化法 → ロンスキー)
\[ \begin{array}{l} y'' + a y' + b y = F(x) \cdots\cdots (1) \\ y = u_1 y_1 + u_2 y_2 \quad が,(1)の解(特殊解)であるとする.\\ y' = u_1' y_1 + u_1 y_1' + u_2' y_2 + u_2 y_2' = (u_1 y_1' + u_2 y_2') + (u_1' y_1 + u_2' y_2)\\ y'' = (u_1 y_1'' + u_2 y_2'') + (u_1' y_1' + u_2' y_2') + (u_1' y_1 + u_2' y_2)' \\ \end{array} \]
\[ \begin{array}{l} (1) \Leftrightarrow \{ (u_1 y_1'' + u_2 y_2'') + (u_1' y_1' + u_2' y_2') + (u_1' y_1 + u_2' y_2)' \} \\ \qquad \qquad + a \{ (u_1 y_1' + u_2 y_2') + (u_1' y_1 + u_2' y_2) \} \\ \qquad \qquad + b \{ u_1 y_1 + u_2 y_2 \} = F(x) \\ \quad \Leftrightarrow u_1(y_1'' + a y_1' + by_1) + u_2(y_2'' + a y_2' + by_2) \\ \qquad \qquad + (u_1' y_1' + u_2' y_2') + (u_1' y_1 + u_2' y_2)' + a(u_1' y_1 + u_2' y_2) = F(x) \\ \qquad \qquad \left\{ \matrix{ u_1' y_1 + u_2' y_2 &=& 0 \cr u_1' y_1' + u_2' y_2' &=& F(x) } \right. \quad \Leftrightarrow \quad \left[\matrix{ y_1 & y_2 \cr y_1' & y_2' }\right] \left[\matrix{ u_1' \cr u_2'}\right] = \left[\matrix{ 0 \cr F(x)}\right] \\ \qquad \qquad \rightarrow \left\{ \matrix{ u_1' \rightarrow u_1 = \int u_1' dx \cr u_2' \rightarrow u_2 = \int u_2' dx } \right. \quad \rightarrow \quad 特殊解 y_0 = u_1 y_1 + u_2 y_2 で求まる. \end{array} \]
\[ \begin{array}{l} \left[\matrix{ y_1 & y_2 \cr y_1' & y_2' }\right] \left[\matrix{ u_1' \cr u_2'}\right] = \left[\matrix{ 0 \cr F(x)}\right] \\ \rightarrow \left[\matrix{u_1' \cr u_2'} \right] = \left[\matrix{y_1 & y_2 \cr y_1' & y_2'} \right]^{-1} \left[\matrix{0 \cr F(x)} \right] = \dfrac{1}{W} \left[\matrix{y_2' & -y_2 \cr -y_1' & y_1} \right] \left[\matrix{0 \cr F(x)} \right] = \dfrac{1}{W} \left[\matrix{-y_2 F(x) \cr y_1 F(x)} \right] \\ \qquad \quad (W = y_1y_2' - y_2y_1') \\ \fbox{$\quad y_0(x) = u_1 y_1 + u_2 y_2 = y_1 \times \left(- \displaystyle \int\dfrac{y_2 F(x)}{W} dx \right) + y_2 \times \left(\displaystyle \int\dfrac{y_1 F(x)}{W} dx \right) \quad $} \end{array} \]
◎~特殊解 \(y_0 = y_0(x)\) の推量による解法 \[ \begin{array}{l} y'' + a y' + b y = F(x) \quad \rightarrow \quad 一般解 y = y_0 + c_1 y_1 + c_2 y_2 \\ y'' + a y' + b y = 0 の基本解 y_1,~ y_2,~ 補助方程式 ~ f(\lambda) = \lambda^2 + a \lambda + b \end{array} \]
\([1]~~ F(x) = k\) (定数) のとき
\[ \begin{array}{l} 1) ~ b \neq 0 ~ のとき, ~ y_0 = \dfrac{k}{b} \\ 2) ~ b = 0 ~かつ ~ a \neq 0~ のとき,~ y_0 = \dfrac{k}{a}x \end{array} \]
\([2]~~ F(x) = k e^{\alpha x}\) のとき
\[ \begin{array}{l} 1) ~ f(\alpha) \neq 0 ~ のとき, y_0 = \dfrac{k}{f(\alpha)}e^{\alpha x} \\ 2) ~ f(\alpha) = 0 ~かつ ~ \lambda = \alpha ~が~ f(\lambda) = 0 ~ の1重解のとき, ~ y_0 = A x e^{\alpha x}\\ ~~~ ~ f(\alpha) = 0 ~かつ ~ \lambda = \alpha ~が~ f(\lambda) = 0 ~ の2重解のとき, ~ y_0 = A x^2 e^{\alpha x} \end{array} \]
\([3]~~ F(x) : x の n 次整式\) のとき
\[ \begin{array}{l} 1) ~ b \neq 0 ~ のとき, y_0 = (x の n 次整式) \\ 2) ~ b = 0 ~かつ ~ a \neq 0~ のとき, y_0 = x \times (x の n 次整式) \end{array} \]
\([4]~~ F(x) = \left\{ \matrix{k \cos \alpha x \cr k \sin \alpha x} \right.\) のとき
\[ \begin{array}{l} 1) ~ f(i \alpha) \neq 0 ~ のとき,~ y_0 = A \cos \alpha x + B \sin \alpha x \\ 2) ~ f(i \alpha) = 0 ~ のとき,~ y_0 = x \times (A \cos \alpha x + B \sin \alpha x) \end{array} \]
◆ 実行例: \(y'' + 2\,y' + 2\,y = e^{2\,x}\)
/home/inoue/bin/go tmp_lang/chunk-174.mx > tmp_lang/chunk-174.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-174.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-174.mx
eq:diff(y(x),x,2)+2*diff(y(x),x)+2*y(x) = %e^(2*x)
ode2(eq,y(x),x)
2 x
- x %e
y(x) = %e (%k1 sin(x) + %k2 cos(x)) + -----
10
/var/www/html/LANG/tmp_lang/chunk-174.mx◆ 実行例: \(y'' - 5\,y' + 4\,y = x^2\)
/home/inoue/bin/go tmp_lang/chunk-175.mx > tmp_lang/chunk-175.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-175.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-175.mx
eq:diff(y(x),x,2)-5*diff(y(x),x)+4*y(x) = x^2
ode2(eq,y(x),x)
2
4 x x 8 x + 20 x + 21
y(x) = %k1 %e + %k2 %e + ----------------
32
/var/www/html/LANG/tmp_lang/chunk-175.mx◆ 実行例: \(y'' - 5\,y' + 4\,y = \cos\,x\)
/home/inoue/bin/go tmp_lang/chunk-176.mx > tmp_lang/chunk-176.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-176.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-176.mx
eq:diff(y(x),x,2)-5*diff(y(x),x)+4*y(x) = cos(x)
ode2(eq,y(x),x)
5 sin(x) - 3 cos(x) 4 x x
y(x) = (- -------------------) + %k1 %e + %k2 %e
34
/var/www/html/LANG/tmp_lang/chunk-176.mx19. 行列と線形代数について
19.1 行列とベクトル
Maxima は行列を扱える. 行列は matrix 命令を用いて宣言する. この matrix 命令は matrxi(行1, 行2, …) の様に行列の行ベクトルをリストの形式でコンマで区切った列を引数とする. 行列の和と差は通常の演算子 \(+\) と演算子 \(-\) を各々用いる. 積演算子 * と商演算子 / は行列の成分同士の 積と商となり, 行列や逆行列との積にはならない点に注意する.
/home/inoue/bin/go tmp_lang/chunk-177.mx > tmp_lang/chunk-177.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-177.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-177.mx
a:matrix([1,0],[0,2])
[ 1 0 ]
[ ]
[ 0 2 ]
b:matrix([1,2],[3,4])
[ 1 2 ]
[ ]
[ 3 4 ]
a+b
[ 2 2 ]
[ ]
[ 3 6 ]
a-b
[ 0 - 2 ]
[ ]
[ - 3 - 2 ]
b*b
[ 1 4 ]
[ ]
[ 9 16 ]
/var/www/html/LANG/tmp_lang/chunk-177.mxそのため, 通常の積演算子 * のことをここでは可換積と呼ぶ. 通常の行列の積演算子は dot 積と呼び, 記号は dot(.) で表す. 例えば, 行列 A と B に対しては, A . B で行列の積を定める. この行列の積に 関しては可換性はない. この dot 積とその他の演算子に関しては環境変数でその分配律や結合律が制御できる. 又, 行列の冪乗は記号^^で記述する. ここで, 行列 A の逆行列が存在する場合, A^^(-1) が行列 A の逆行列に なる. ベクトルは share/vector/ にベクトル解析パッケージが含まれている. ベクトル解析パッケー ジの 読込は load(vect) で行なう. ベクトル解析パッケー ジを使えば内積と外積, 勾配, 発散, 回転 や laplace 演算子を含む記号式のまとめと簡約化が行える様になる. これらの演算子の和や積に対する分配は, 利用者指定で 制御できる. なお, スカラー値や場のベクトルの微分も可能である. このパッケージは次の命令を含んでいる. vectorsimp, scalefactors, express, potential と vectorpotential. ここで注意することに, vect パッケージの読込みを行うと dot 演算子が行列の非可換積では無く, 可換演算子であると宣言してしまう ことである.
19.2 行列操作の実行例
◆ 行列の定義1
/home/inoue/bin/go tmp_lang/chunk-178.mx > tmp_lang/chunk-178.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-178.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-178.mx
M:matrix([a,b],[c,d])
[ a b ]
[ ]
[ c d ]
/var/www/html/LANG/tmp_lang/chunk-178.mx◆ 行列の定義2
/home/inoue/bin/go tmp_lang/chunk-179.mx > tmp_lang/chunk-179.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-179.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-179.mx
h[i,j]:=i+j-1
A:genmatrix(h,3,3)
[ 1 2 3 ]
[ ]
[ 2 3 4 ]
[ ]
[ 3 4 5 ]
B:genmatrix(h,3,3,2,1)
[ 2 3 4 ]
[ ]
[ 3 4 5 ]
/var/www/html/LANG/tmp_lang/chunk-179.mx行列 B は h[i,j] の添字を i=2,3, j=1,2,3 とした要素からなる行列を生成する.
◆ 行列の基本演算
/home/inoue/bin/go tmp_lang/chunk-180.mx > tmp_lang/chunk-180.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-180.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-180.mx
A:matrix([a11,a12],[a21,a22])
[ a11 a12 ]
[ ]
[ a21 a22 ]
B:matrix([b11,b12],[b21,b22])
[ b11 b12 ]
[ ]
[ b21 b22 ]
b:matrix([b1],[b2])
[ b1 ]
[ ]
[ b2 ]
A+B
[ b11 + a11 b12 + a12 ]
[ ]
[ b21 + a21 b22 + a22 ]
A-B
[ a11 - b11 a12 - b12 ]
[ ]
[ a21 - b21 a22 - b22 ]
A . b
[ a12 b2 + a11 b1 ]
[ ]
[ a22 b2 + a21 b1 ]
"/* 注:A^^2 */"
A^^2
[ 2 ]
[ a12 a21 + a11 a12 a22 + a11 a12 ]
[ ]
[ 2 ]
[ a21 a22 + a11 a21 a22 + a12 a21 ]
"/* 注:A^^(-1) */"
A^^(-1)
[ a22 a12 ]
[ ----------------- - ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
[ ]
[ a21 a11 ]
[ - ----------------- ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
invert(A)
[ a22 a12 ]
[ ----------------- - ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
[ ]
[ a21 a11 ]
[ - ----------------- ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
doallmxops:false
dosmxops:false
detout:true
invert(A)
[ a22 - a12 ]
[ ]
[ - a21 a11 ]
-----------------
a11 a22 - a12 a21
/var/www/html/LANG/tmp_lang/chunk-180.mx◆ リストから列ベクトルを生成する
/home/inoue/bin/go tmp_lang/chunk-181.mx > tmp_lang/chunk-181.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-181.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-181.mx
load(eigen)
columnvector([x1,x2])
[ x1 ]
[ ]
[ x2 ]
/var/www/html/LANG/tmp_lang/chunk-181.mx◆ 行ベクトル,列ベクトルの生成
/home/inoue/bin/go tmp_lang/chunk-182.mx > tmp_lang/chunk-182.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-182.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-182.mx
A:matrix([a11,a12],[a21,a22])
row(A,1)
[ a11 a12 ]
col(A,2)
[ a12 ]
[ ]
[ a22 ]
/var/www/html/LANG/tmp_lang/chunk-182.mx◆ 対角行列,単位行列,零行列,転置行列,部分行列
/home/inoue/bin/go tmp_lang/chunk-183.mx > tmp_lang/chunk-183.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-183.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-183.mx
diagmatrix(2,c)
[ c 0 ]
[ ]
[ 0 c ]
M:matrix([m11,m12],[m21,m22])
diagmatrix(2,M)
[ [ m11 m12 ] ]
[ [ ] 0 ]
[ [ m21 m22 ] ]
[ ]
[ [ m11 m12 ] ]
[ 0 [ ] ]
[ [ m21 m22 ] ]
ident(2)
[ 1 0 ]
[ ]
[ 0 1 ]
zeromatrix(2,3)
[ 0 0 0 ]
[ ]
[ 0 0 0 ]
A:matrix([a11,a12],[a21,a22],[a31,a32])
M:transpose(A)
[ a11 a21 a31 ]
[ ]
[ a12 a22 a32 ]
submatrix(1,M,2)
[ a12 a32 ]
/var/www/html/LANG/tmp_lang/chunk-183.mx◆ 行列式の値
/home/inoue/bin/go tmp_lang/chunk-184.mx > tmp_lang/chunk-184.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-184.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-184.mx
M:matrix([a,b],[c,d])
determinant(M)
a d - b c
/var/www/html/LANG/tmp_lang/chunk-184.mx◆ 余因子行列
/home/inoue/bin/go tmp_lang/chunk-185.mx > tmp_lang/chunk-185.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-185.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-185.mx
M:matrix([a,b],[c,d])
adjoint(M)
[ d - b ]
[ ]
[ - c a ]
/var/www/html/LANG/tmp_lang/chunk-185.mx◆ 方程式から係数行列を生成
/home/inoue/bin/go tmp_lang/chunk-186.mx > tmp_lang/chunk-186.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-186.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-186.mx
augcoefmatrix([a11*x+a12*y = b1,a21*x+a22*y = b2],[x,y])
[ a11 a12 - b1 ]
[ ]
[ a21 a22 - b2 ]
/var/www/html/LANG/tmp_lang/chunk-186.mx◆ 特性多項式を変数に対して求める
/home/inoue/bin/go tmp_lang/chunk-187.mx > tmp_lang/chunk-187.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-187.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-187.mx
A:matrix([3,1],[2,4])
eq1:expand(charpoly(A,t))
2
t - 7 t + 10
(programmode:true,ans:solve(eq1))
[t = 5, t = 2]
x:matrix([x1],[x2])
eq2:ev(A . x-t*x,ans[1])
[ x2 - 2 x1 ]
[ ]
[ 2 x1 - x2 ]
eq3:eq2[1,1] = 0
x2 - 2 x1 = 0
eq4:x1^2+x2^2 = 1
2 2
x2 + x1 = 1
solve([eq3,eq4],[x1,x2])
1 2 1 2
[[x1 = - -------, x2 = - -------], [x1 = -------, x2 = -------]]
sqrt(5) sqrt(5) sqrt(5) sqrt(5)
/var/www/html/LANG/tmp_lang/chunk-187.mx◆ 連立1次方程式の係数行列
/home/inoue/bin/go tmp_lang/chunk-188.mx > tmp_lang/chunk-188.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-188.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-188.mx
coefmatrix([a*x+b*y = 0,c*x+d*y = 0],[x,y])
[ a b ]
[ ]
[ c d ]
/var/www/html/LANG/tmp_lang/chunk-188.mx◆ ベクトル X の複素共役を返す
/home/inoue/bin/go tmp_lang/chunk-189.mx > tmp_lang/chunk-189.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-189.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-189.mx
load(eigen)
X:matrix([a],[b1+b2*%i])
conjugate(X)
[ a ]
[ ]
[ b1 - %i b2 ]
/var/www/html/LANG/tmp_lang/chunk-189.mx◆ 行列の複製をつくる.
/home/inoue/bin/go tmp_lang/chunk-190.mx > tmp_lang/chunk-190.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-190.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-190.mx
A:matrix([a11,a12],[a21,a22])
B:copymatrix(A)
[ a11 a12 ]
[ ]
[ a21 a22 ]
C:setelmx(c,1,2,A)
[ a11 c ]
[ ]
[ a21 a22 ]
/var/www/html/LANG/tmp_lang/chunk-190.mx複製と同時に一部を変更した行列を作成するには setelmx を用いる.
◆ 行列への行ベクトル,列ベクトルの追加
/home/inoue/bin/go tmp_lang/chunk-191.mx > tmp_lang/chunk-191.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-191.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-191.mx
A:matrix([a11,a12],[a21,a22])
addrow(A,[b1,b2])
[ a11 a12 ]
[ ]
[ a21 a22 ]
[ ]
[ b1 b2 ]
addcol(A,[b1,b2])
[ a11 a12 b1 ]
[ ]
[ a21 a22 b2 ]
/var/www/html/LANG/tmp_lang/chunk-191.mx◆ 行列の上三角化: Echelon 形式
/home/inoue/bin/go tmp_lang/chunk-192.mx > tmp_lang/chunk-192.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-192.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-192.mx
M:matrix([a,b,c],[d,e,f])
echelon(M)
[ b c ]
[ 1 - - ]
[ a a ]
[ ]
[ a f - c d ]
[ 0 1 --------- ]
[ a e - b d ]
triangularize(M)
[ a b c ]
[ ]
[ 0 a e - b d a f - c d ]
/var/www/html/LANG/tmp_lang/chunk-192.mx◆ 固有値・固有ベクトル
/home/inoue/bin/go tmp_lang/chunk-193.mx > tmp_lang/chunk-193.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-193.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-193.mx
M:matrix([a,b],[b,a])
eigenvalues(M)
[[a - b, b + a], [1, 1]]
eigenvectors(M)
[[[a - b, b + a], [1, 1]], [[[1, - 1]], [[1, 1]]]]
/var/www/html/LANG/tmp_lang/chunk-193.mxeigenvalues(M) では,結果を,[[固有値1,固有値2],[重複度1,重複度2]]の形式で返し,eigenvectors(M) では,結果を,[[固有値1,固有値2],[重複度1,重複度2]], 固有ベクトル1,固有ベクトル2] の形式で返す.
◆ 固有値分解:基準化
/home/inoue/bin/go tmp_lang/chunk-194.mx > tmp_lang/chunk-194.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-194.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-194.mx
load(eigen)
M:matrix([a,b],[b,a])
uniteigenvectors(M)
1 1 1 1
[[[a - b, b + a], [1, 1]], [[[-------, - -------]], [[-------, -------]]]]
sqrt(2) sqrt(2) sqrt(2) sqrt(2)
/var/www/html/LANG/tmp_lang/chunk-194.mx◆ ベクトルの正規化(長さ1に基準化)
/home/inoue/bin/go tmp_lang/chunk-195.mx > tmp_lang/chunk-195.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-195.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-195.mx
unitvector([a,b])
unitvector([a, b])
/var/www/html/LANG/tmp_lang/chunk-195.mx◆ Gram-Schmidt のアルゴリズム(直交化)
/home/inoue/bin/go tmp_lang/chunk-196.mx > tmp_lang/chunk-196.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-196.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-196.mx
load(eigen)
M:matrix([a,b],[b,a])
gramschmidt(M)
b (b - a) (b + a) a (b - a) (b + a)
[[a, b], [-----------------, - -----------------]]
2 2 2 2
b + a b + a
/var/www/html/LANG/tmp_lang/chunk-196.mx◆ 内積
/home/inoue/bin/go tmp_lang/chunk-197.mx > tmp_lang/chunk-197.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-197.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-197.mx
load(eigen)
x:matrix([x1],[x2])
y:matrix([y1],[y2])
innerproduct(x,y)
x2 y2 + x1 y1
x . y
x2 y2 + x1 y1
/var/www/html/LANG/tmp_lang/chunk-197.mx外積については拡張機能を参照.
◆ 逆行列:余因子行列を用いる.
/home/inoue/bin/go tmp_lang/chunk-198.mx > tmp_lang/chunk-198.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-198.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-198.mx
print(" invert(M) := adjoint(M) / determinant(M) ")
invert(M) := adjoint(M) / determinant(M)
M:matrix([a11,a12],[a21,a22])
adjoint(M)
[ a22 - a12 ]
[ ]
[ - a21 a11 ]
determinant(M)
a11 a22 - a12 a21
Minv:adjoint(M)/determinant(M)
[ a22 a12 ]
[ ----------------- - ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
[ ]
[ a21 a11 ]
[ - ----------------- ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
invert(M)
[ a22 a12 ]
[ ----------------- - ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
[ ]
[ a21 a11 ]
[ - ----------------- ----------------- ]
[ a11 a22 - a12 a21 a11 a22 - a12 a21 ]
/var/www/html/LANG/tmp_lang/chunk-198.mx◆ トレース:正方行列の対角成分の和を求める
/home/inoue/bin/go tmp_lang/chunk-199.mx > tmp_lang/chunk-199.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-199.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-199.mx
load(nchrpl)
M:matrix([a11,a12],[a21,a22])
mattrace(M)
a22 + a11
/var/www/html/LANG/tmp_lang/chunk-199.mx◆ 小行列:行列から,ある行,ある列を除いた小行列を生成する
/home/inoue/bin/go tmp_lang/chunk-200.mx > tmp_lang/chunk-200.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-200.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-200.mx
M:matrix([a11,a12,a13],[a21,a22,a23])
minor(M,1,2)
[ a21 a23 ]
/var/www/html/LANG/tmp_lang/chunk-200.mx◆ 階数(ランク)
/home/inoue/bin/go tmp_lang/chunk-201.mx > tmp_lang/chunk-201.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-201.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-201.mx
M:matrix([1,2,3],[2,4,6])
rank(M)
1
/var/www/html/LANG/tmp_lang/chunk-201.mx◆ 1x1 行列をスカラーに変換する
/home/inoue/bin/go tmp_lang/chunk-202.mx > tmp_lang/chunk-202.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-202.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-202.mx
scalarmatrixp:false
matrix([a1,a2]) . matrix([b1],[b2])
[ a2 b2 + a1 b1 ]
scalarmatrixp:true
matrix([a1,a2]) . matrix([b1],[b2])
a2 b2 + a1 b1
/var/www/html/LANG/tmp_lang/chunk-202.mx19.3 行列操作の追加機能
本節で取り上げる機能は,私用ライブラリ MATLIB.mx にまとめられている.
外積
/home/inoue/bin/go tmp_lang/chunk-203.mx > tmp_lang/chunk-203.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-203.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-203.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-203.mxリストのベクトル化
/home/inoue/bin/go tmp_lang/chunk-204.mx > tmp_lang/chunk-204.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-204.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-204.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-204.mx行列の次元
/home/inoue/bin/go tmp_lang/chunk-205.mx > tmp_lang/chunk-205.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-205.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-205.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-205.mx対称行列の固有値分解 \(A' A \,=\, G\, D\, G'\)
/home/inoue/bin/go tmp_lang/chunk-206.mx > tmp_lang/chunk-206.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-206.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-206.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-206.mx特異値分解 \(X \,=\, Z\, \Lambda^{1/2}\, G'\)
/home/inoue/bin/go tmp_lang/chunk-207.mx > tmp_lang/chunk-207.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-207.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-207.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-207.mx射影子 \(Q = X\,(X'\,X)^{-1}\,X'\)
\((X'X)^{-1}\) が存在しない場合には,特異値分解 \(X = Z\,D\,G'\) を用いて, \(Q = Z\,Z'\) として求められる.
/home/inoue/bin/go tmp_lang/chunk-208.mx > tmp_lang/chunk-208.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-208.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-208.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-208.mx一般逆行列 \(X^{-1} = (X'\,X)^{-1}\,X'\)
\((X'X)^{-1}\) が存在しない場合には,特異値分解 \(X = Z\,D\,G'\) を用いて, \(X^{-} = G\,D^{-1}\,Z'\) として求められる.関係式 \(X\,X^{-}\,X = X\), \(X^{-}\,X\,X^{-} = X^{-}\) が成り立つ.
/home/inoue/bin/go tmp_lang/chunk-209.mx > tmp_lang/chunk-209.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-209.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-209.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-209.mx掃き出し法(教育用)
/home/inoue/bin/go tmp_lang/chunk-210.mx > tmp_lang/chunk-210.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-210.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-210.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-210.mx行列の基本操作
/home/inoue/bin/go tmp_lang/chunk-211.mx > tmp_lang/chunk-211.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-211.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-211.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-211.mx/home/inoue/bin/go tmp_lang/chunk-212.mx > tmp_lang/chunk-212.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-212.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-212.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-212.mx基底の変換と表現行列
%* 基底の変換と表現行列 桑村 p.178 参照 * 平面\(X\)上の点\((x_1,\,x_2)\) を平面\(Y\)上の点\((y_1,\,y_2)\) に移す線型写像(1次変換) \(f\) \[ \pmatrix{y_1 \cr y_2} = f(\pmatrix{x_1 \cr x_2}) = \pmatrix{x_1+x_2 \cr x_1-x_2} \] を考える.平面\(X,\, Y\)上の基底をそれぞれ \(\{\mathbf{a}_1,\, \mathbf{a}_2\} = \{(1, -1),\, (1, 0)\}\), \(\{\mathbf{b}_1,\, \mathbf{b}_2\} = \{(0, -1),\, (1, 2)\}\) とする.このとき,\(f : X \rightarrow Y\) の表現行列 \(C\) は次式で表せる. \[ f(\mathbf{a}_1) = f(\pmatrix{1 \cr -1}) = \pmatrix{0 \cr 2}, \quad f(\mathbf{a}_2) = f(\pmatrix{1 \cr 0}) = \pmatrix{1 \cr 1}, \] \[ (f(\mathbf{a}_1),\, f(\mathbf{a}_2)) = (\mathbf{b}_1,\, \mathbf{b}_2)\, C ~\Leftrightarrow ~ \pmatrix{0 & 1 \cr 2 & 1} = \pmatrix{0 & 1 \cr -1 & 2} \, C \] \[ ~\Leftrightarrow ~ C = \pmatrix{0 & 1 \cr -1 & 2}^{-1}\, \pmatrix{0 & 1 \cr 2 & 1} = \pmatrix{2 & -1 \cr 1 & 1}\, \pmatrix{0 & 1 \cr 2 & 1} = \pmatrix{-2 & 1 \cr 0 & 1} \] 次に,平面\(X,\, Y\)上の新基底をそれぞれ \(\{\mathbf{a}_1',\, \mathbf{a}_2'\} = \{(0, 1),\, (1, 1)\}\), \(\{\mathbf{b}_1',\, \mathbf{b}_2'\} = \{(-1, 1),\, (1, 0)\}\) とすると,新基底に関する\(f\) の表現行列 \(C'\) は次式で表せる. \[ f(\mathbf{a}_1') = f(\pmatrix{0 \cr 1}) = \pmatrix{1 \cr -1}, \quad f(\mathbf{a}_2') = f(\pmatrix{1 \cr 1}) = \pmatrix{2 \cr 0}, \] \[ (f(\mathbf{a}_1'),\, f(\mathbf{a}_2')) = (\mathbf{b}_1',\, \mathbf{b}_2')\, C' ~\Leftrightarrow ~ \pmatrix{1 & 2 \cr -1 & 0} = \pmatrix{-1 & 1 \cr 1 & 0} \, C' \] \[ ~\Leftrightarrow ~ C' = \pmatrix{-1 & 1 \cr 1 & 0}^{-1}\, \pmatrix{1 & 2 \cr -1 & 0} = \pmatrix{0 & -1 \cr -1 & -1}\, \pmatrix{1 & 2 \cr -1 & 0} = \pmatrix{-1 & 0 \cr 0 & 2} \] ところで,基底変換は行列\(P,\, Q\) を用いてそれぞれ次式で表せる. \[ (\mathbf{a}_1',\, \mathbf{a}_2' ) = (\mathbf{a}_1,\, \mathbf{a}_2 )\, P, ~\Leftrightarrow ~ \pmatrix{0 & 1 \cr 1 & 1} = \pmatrix{1 & 1 \cr -1 & 0}\, P ~\Leftrightarrow ~ P = \pmatrix{-1 & -1 \cr 1 & 2} \] \[ (\mathbf{b}_1',\, \mathbf{b}_2' ) = (\mathbf{b}_1,\, \mathbf{b}_2 )\, Q ~\Leftrightarrow ~ \pmatrix{-1 & 1 \cr 1 & 0} = \pmatrix{0 & 1 \cr -1 & 2}\, Q ~\Leftrightarrow ~ Q = \pmatrix{-3 & 2 \cr -1 & 1} \] これを用いると,表現行列 \(C\) と \(C'\) の間に以下の関係式を得る. \[ 着目:~~f(\mathbf{a}_1') = f(\mathbf{a}_1\,p_{11} + \mathbf{a}_2\,p_{21}) = f(\mathbf{a}_1)\,p_{11} + f(\mathbf{a}_2)\,p_{21}, \] \[\qquad ~~ ~~f(\mathbf{a}_2') = f(\mathbf{a}_2\,p_{12} + \mathbf{a}_2\,p_{22}) = f(\mathbf{a}_2)\,p_{12} + f(\mathbf{a}_2)\,p_{22} \] \[ (f(\mathbf{a}_1'),\, f(\mathbf{a}_2')) = (f(\mathbf{a}_1\,P),\, f(\mathbf{a}_2\,P)) = (f(\mathbf{a}_1),\, f(\mathbf{a}_2))\, P = (\mathbf{b}_1,\, \mathbf{b}_2 )\, C\, P \] \[ (f(\mathbf{a}_1'),\, f(\mathbf{a}_2')) = (\mathbf{b}_1',\, \mathbf{b}_2' )\, C' = (\mathbf{b}_1,\, \mathbf{b}_2 )\, Q \, C' \] \[ ∴ ~~ Q\,C' = C\,P ~\Leftrightarrow ~ C' = Q^{-1}\,C \, P \]
/home/inoue/bin/go tmp_lang/chunk-213.mx > tmp_lang/chunk-213.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-213.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-213.mx
batchload("/home/inoue/Max-ex/MATLIB.mx")
file_search1: /home/inoue/Max-ex/MATLIB.mx not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-213.mx19.4 関連する環境変数
● detout:false
true であれば,
逆行列を計算したときに行列式の割算がそのまま行列の外に残される.
この環境変数が 効力を持つためには doallmxops と doscmxops が false
でなければならない. この設定を ev で与える こともできる.
● doallmxops:true
true であれば, 全ての行列演算子が評価される. false であれば, 演算子を
支配する個々の dot 環境変数の設定が実行される.
● domxexpt:true
true の場合, %e^matrix([1,2],[3,4]) は
matrix([%e,%e^2],[%e3,%e4]) となる.
一般的 に, この変換は<基底>^<羃> の形式の変換に影響する. なお,
基底はスカラか定数の式であり, 羃はリストか行列である. false であれば,
この変換は実行されない.
● domxmxops:true
true であれば,
行列と行列間の演算子や行列とリストの間の演算子が実行される.false
であれば, これらの演算は実行されない.
この環境変数はスカラーと行列との間の演算には影響を与えない.
● domxnctimes:false false であれば行列の非可換積が実行される.
● doscmxops:false
true であればスカラと行列間の演算子が実行される.
● doscmxplus:false
true であれば, スカラ+行列が行列値となる. この環境変数は doallmxops
と独立した変数である.
● lmxchar:[
行列の (左) の括弧として表示する文字を設定する. 右側は rmxchar
で指定する.
● rmxchar:]
行列の (右) の括弧として表示する文字を設定する. 左側は lmxchar
で指定する.
● matrix_element_add:+
matrix_element_add は行列同士の和を計算する演算子を設定する.
● matrix_element_mult:* matrix_element_mult は行列の成分同士の積を計算する演算子を設定する.
● matrix_element_transpose:false
別の便利な設定は transpose と nonscalars; であり, 関数名や lambda
式であっても良い. こうすることで 様々な代数的構造が扱える.
● ratmx:false
false であれば, 行列式や行列の和, 差, 積が行列の表示形式で行われ,
逆行列の結果も一般の表示となる. true であれば, これらの演算は CRE
形式で行われて逆行列の結果も CRE 形式となる. これは成分が往々にして
望みもしない展開 (ratfac の設定に依存するものの)
の原因となるかもしれない.
● scalarmatrixp:true
true であれば, 二つの行列の dot 積の計算で得られた 1x1
行列はスカラーに変換される. all であれば, この変換は 1x1
行列は常にスカラーに実行される. false に設定されていれば,
この変換は実行されない.
● sparse:false true でかつ ratmx:true であれば, determinant は疎行列式を計算するためのルーチンを利用する.
● vect_cross:false
true であれば diff(x~y,y) が使える. ここで, ~ は share;vect
で定義されている.
19.5 関連する関数
● addcol(Mat, L_1, L_2, … , L_n)
● addrow(Mat, L_1, L_2, … , L_n)
addcol は列として, addrow は行として,
複数の複数のリストや行列を行列に追加する. なお, 追加するリストや行列は,
行列Matの大きさと矛盾しないものでなければならない.
● adjoint(Mat)
行列Matの余因子行列を計算する.
● augcoefmatrix([eq_1, …],[var_1, …])
与えられた方程式eq_iと指定した変数var_iのリストから, 係数行列を生成する.
行列は, 方程式eq_1,..から
構成される線形方程式系に含まれる変数var_1,…の係数から構築される.
この係数行列には各方程式の定数項が 列として付け加えられている.
● charpoly(Mat, var)
行列の特性多項式 det( I -
● coefmatrix([eq_1,…], [var_1,…])
連立一次方程式の変数リストに対応する係数行列を返す.
● col(Mat, i)
行列Matの i 番目の列を返す.
● columnvector(List)
予め load(eigen) を実行する. columnvector はリストListを引数とし,
引数リストを成分とする 列ベクトルを返す.
● conjugate(List)
eigen パッケージの関数である. conjugate は引数の複素共役を返す.
● copymatrix(Mat)
行列Matの複製を作成する.
この命令は行列Matを成分毎に再生成するときに使われる.
一部を変更した行列の複製では setmelmx を使うと便利である.
● determinant(Mat)
gauss の消去法と似た方法で行列Matの行列式を計算する.
計算結果の書式は環境変数 ratmx の設定に依存する.
疎行列の行列式を計算する特別な方法もあり,ratmx:true と sparse:true
と設定した場合に使える.
● diagmatrix(n, Mat)
第2引数で指定した行列Matを対角に n 個並べた行列を返す. diagmatrix(n,1)
は ident(n) と同じ n 次元の 単位行列を返す.
● echelon(Mat)
行列Matの echelon 形式を返す.
これは初等的な行操作で各々の行の最初の非零元を 1, その元を含む列に
対してはその元を含む行よりも下の成分を全て零となる様に変形する
(上三角行列).
/home/inoue/bin/go tmp_lang/chunk-214.mx > tmp_lang/chunk-214.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-214.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-214.mx
M:matrix([a,b,c],[d,e,f])
[ a b c ]
[ ]
[ d e f ]
echelon(M)
[ b c ]
[ 1 - - ]
[ a a ]
[ ]
[ a f - c d ]
[ 0 1 --------- ]
[ a e - b d ]
/var/www/html/LANG/tmp_lang/chunk-214.mx● eigenvalues(Mat)
行列 Mat の固有値と重複度を求め,結果をリスト [[固有値1,固有値2, …],
[重複度1, 重複度2, …]] で返す.
● eigenvectors(Mat)
行列Mat の固有値(重複度)と固有ベクトルを求め,結果をリスト
[[固有値1,固有値2, …], [重複度1, 重複度2, …], 固有ベクトル1,
固有ベクトル2, …] で返す.
● ematrix(m, n, x, i, j)
m 行 n 列の行列で i 行 j 列成分のみが x ,
他が全て零となる行列を返す.
● entermatrix(m, n)
Maxima の要求に従って m × n 個の成分を入力して行列を生成する.
● genmatrix(array, i2, j2, i1, j1)
配列arrayから行列を生成する. ここで配列 array(i1, j1) は最初(左側上)
の元 array(i2, j2) が 残り(左下)の元となる. j1 = i1 であれば, j1
は削除される. j1 = i1 = 1 ならば, i1 と j1 の両方が
省略されることもある. 配列の元が不足した場合には,
記号的な元が使わる.
/home/inoue/bin/go tmp_lang/chunk-215.mx > tmp_lang/chunk-215.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-215.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-215.mx
h[i,j]:=1/(i+j-1)
genmatrix(h,3,3)
[ 1 1 ]
[ 1 - - ]
[ 2 3 ]
[ ]
[ 1 1 1 ]
[ - - - ]
[ 2 3 4 ]
[ ]
[ 1 1 1 ]
[ - - - ]
[ 3 4 5 ]
/var/www/html/LANG/tmp_lang/chunk-215.mx● gramschmidt([L_1,…,L_n])
予め load(eigen) を実行する.長さの等しいリスト [L_1,…,L_n]
に対して,互いに直交したリストを返す.
なお、返す結果には因子分解された整数が含まれることがある. これは Maxima
の factor 関数が gram-schmidt の処理の過程で使われたためである.
こうすることで式が複雑なものになることを回避し,
生成される変数の大きさを減らす助けになる.
● hach(a,b,m,n,l)
Hacijan の線型プログラミングアルゴリズムの実装. 予め load(hach)
を実行する.
● ident(n)
n 行 n 列の単位行列を返す.
● innerproduct(x, y)
予め load(eigen) を実行する. 長さの等しい2つのリスト x と y に対して,
「(x の複素共役) . y」 で定義されている内積を返す. ここで, dot
演算子は通常のベクトルの内積演算子と同じである.
● invert(Mat)
行列 Mat の逆行列を余因子行列を用いた方法で求め,結果を返す. これは boat
値成分や浮動小数点を 係数とする多項式を成分とする行列の逆行列を CRE
形式に変換せずに計算できる. determinant 命令は
余因子の計算で利用されるので, ratmx が false ならば,
その逆行列は成分表現を変更せずに計算される.
現行の実装は高い次数の行列に対して効率的なものではない. detout フラグが
true であれば行列式の部分は 逆行列の外側に出されたままとなる. invert
が返した結果は展開されていない. 最初から多項式成分を持つ行列 の場合,
expand(invert(mat)), detout で生成された出力は見栄えが良くなる.
行列式で割られた方が望ましい 場合, xthru(%) を併用したり,
expand(adjoint(行列))/expand(determinant(行列)) で計算すると良い.
● matrix(row_1,… , row_n)
指定した行row_iを持つ行列を定義する.
● matrixmap(func, Mat)
行列Matの各成分に関数funcを作用させる.
● matrixp(exp)
式expが行列であれば true, そうでなければ false を返す.
● mattrace(Mat)
正方行列Matの対角和(行列の主対角成分の総和)を返す.
● minor(Mat, i, j)
行列Matの i , j 成分の小行列, つまり, 行列から i 行と j
列を抜いた小行列を返す.
● ncexpt(Mat_1, Mat_2)
Mat_1 ^^ Mat_2 を(非可換)指数式で表示する際に, 大き過ぎれば
ncexpt(Mat_1, Mat_2) が用いられる.
● ncharpoly(Mat, var) 変数varに対する行列Matの特性多項式を返す.これは Maxima の charpoly とは別物である. 予め load(”nchrpl”) を実行する.
● newdet(Mat, n)
行列(配列)Matの行列式を返す. この際に, Johnson-Gentleman tree minor
アルゴリズムを用いる. Matは行列か配列の何れかで, n
は行列の大きさになる.
● nonscalarp(exp)
式expが非スカラ, つまり, 原子を含み,
非スカラと宣言されたリストや行列であれば true を返し, スカラの場合は
false を返す.
● permanent(Mat, n)
行列Matの permanent を計算する. permanent は行列式に似ているが,
符号の変化はない.
● rank(Mat)
行列Matの階数を返す. なお, rank
は行列成分の値が非常に零に近い場合には誤った答を返すことがある.
● row(Mat, i)
行列Matの i 番目の行を返す.
● scalarp(exp)
true となるのは, 式expが数, 定数やスカラーとして宣言された変数, 数,
定数, そしてその様な変数の合成で 行列やリストを含まない場合である.
● setelmx(x, i, j, Mat)
行列Matの i 行 j 列成分を x で置き換えた行列を返す. なお,
直接行列の成分を指定して置換えることもできる. この場合, A[i,j]:x で行列
A の (i,j) 成分を x で置換する. ただし, この場合の返却値は x になる.
● similaritytransform(Mat)
予め, load(eigen) を実行する.行列Matに対し,
uniteigenvectors(Mat)の出力リストを返す. 環境変数が
nondiagonalizable:false であれば, 二つの行列 L と R が生成される. この L
と R は, L . Mat . R が対角行列となり,
行列Matの固有値が対角成分に現れる. nondiagonalizable:true であれば,
これらの行列は生成されない. 環境変数が hermitianmatrix:true で あれば, L
は R の複素共役の転置となる. false であれば, L は R の逆行列になる. R は
行列 Mat の正規化した固有ベクトルを列とする行列になる.
● submatrix(row_1,…, row_m, col_1,…, col_n)
行row_iと列col_jが削除された小行列を返す.
● transpose(Mat)
行列Matの転置行列を返す.
● triangularize(Mat)
行列Matの上三角行列形式を返す. 行列が正方行列である必要はない.
● uniteigenvectors(Mat)
予め load(eigen) を実行する. 行列 Mat
の固有値と「正規化された」固有ベクトルで構成されたリストを返す.
eigenvectors 関数の詳細で述べた環境変数はここでも同様の影響を与える.
● unitvector(List)
予め load(eigen) を実行する.unitvector はリストListを正規化したリスト,
即ち, その大きさを 1 にした リストを返す.
● vectorsimp(Vec)
この関数は和の簡約化で様々な環境変数の設定と共に用いる.
ここで式は以下の環境変数の設定に関連する.
全てのこれらの環境変数はデフォルト値として false が設定されている. 後に plus の付く環境変数は加法性と 被演算子の分配性に関連する. 同様に, 後に prod の付く環境変数はあらゆる種類の積演算に対する被演算子への 分配性に関連する.
● zeromatrix(m, n)
引数として整数値の m , n を取って m 行 n 列の零行列を返す.