Maxima レファレンス・マニュアル(暫定第3.3版)
INOUE Takakatsu 2024-05-15
索引
20. 作図1 plot
20.1 作図関数(plot2d, plot3d)
20.1.1 2次元プロット(plot2d)
● plot2d(exp,range,…,options,..)
● plot2d([exp_1,exp_2,..,exp_n],xrange,…,options,..)
● plot2d(parametric_exp)
expr は y 軸について 1 変数の関数としてグラフ表示される式である. range
は [var, min, max] の形式で あり, exp は var
に対してグラフ表示される式である. 二番目の plot2d 関数の形式で, 式の
リストは表示するために与えても良い. y 方向での切り捨てはデフォルト 値の
y の領域に対して行われる. これは option や set_plot_option
を用いて指定できる.
◆ 実行例:関数 \(y = f(x)\) の表示
/home/inoue/bin/go tmp_lang/chunk-1.mx > tmp_lang/chunk-1.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-1.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-1.mx
set_plot_option([plot_format,gnuplot])
set_plot_option(['gnuplot_ps_term_command,
"set size 1.2, 1.2; set term postscript eps enhanced color solid 28"])
"/* size: 1.2, 1.2 (画面サイズ:1.5, 1.5), 28:(フォントサイズ:24) */"
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-1.png"])
plot2d(sin(x),[x,-5,5])
/var/www/html/LANG/tmp_lang/chunk-1.mx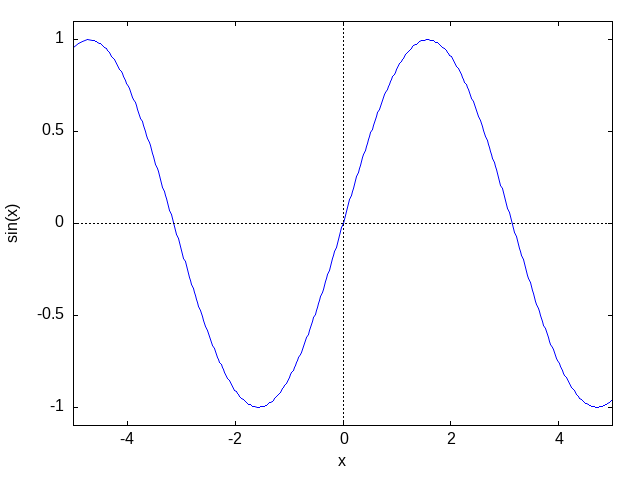
図20.11. Max-ref-3_files/fig20-1.png
更に, exp に媒介変数表示(助変数式) \(x = x(t), y = y(t)\) を用いても良い: parametric_exp は [parametric, xexp, yexp, trange, … options] の形式のリストで指定する.
◆ 実行例:媒介変数による関数 \((x=x(t),\,y=y(t))\) の表示
/home/inoue/bin/go tmp_lang/chunk-2.mx > tmp_lang/chunk-2.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-2.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-2.mx
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-2a.png"])
plot2d([parametric,cos(t),sin(t),[t,(-%pi)*2,%pi*2]])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-2b.png"])
plot2d([parametric,cos(t),sin(t),[t,(-%pi)*2,%pi*2]],['nticks,10])
/var/www/html/LANG/tmp_lang/chunk-2.mx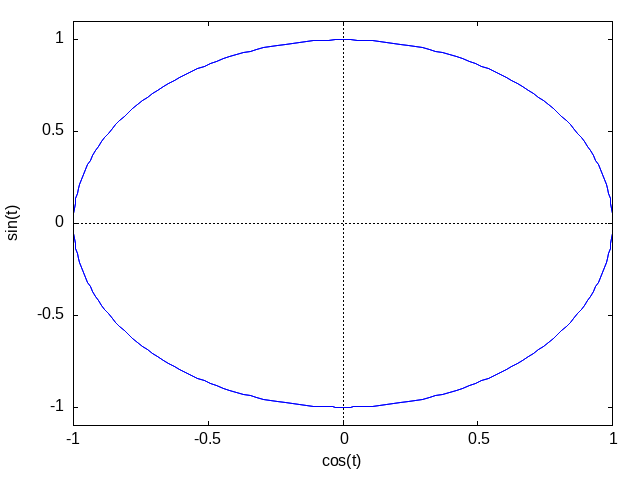
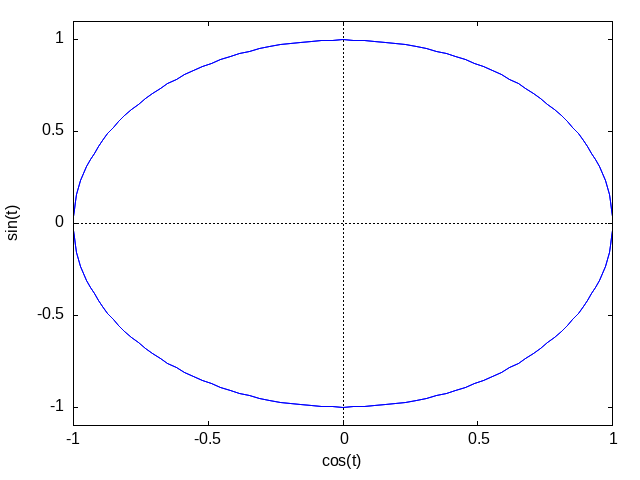
図20.12. Max-ref-3_files/fig20-2.png
◆ 実行例:通常関数 \(y = f(x)\) と媒介変数による関数 \((x=x(t),\,y=y(t))\) の同時表示
/home/inoue/bin/go tmp_lang/chunk-3.mx > tmp_lang/chunk-3.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-3.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-3.mx
display2d:false
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-3.png"])
plot2d([x^3+2,[parametric,cos(t),sin(t),[t,-5,5]]],[x,-2,2],[nticks,80])
"/var/www/html/LANG/tmp_lang/chunk-3.mx"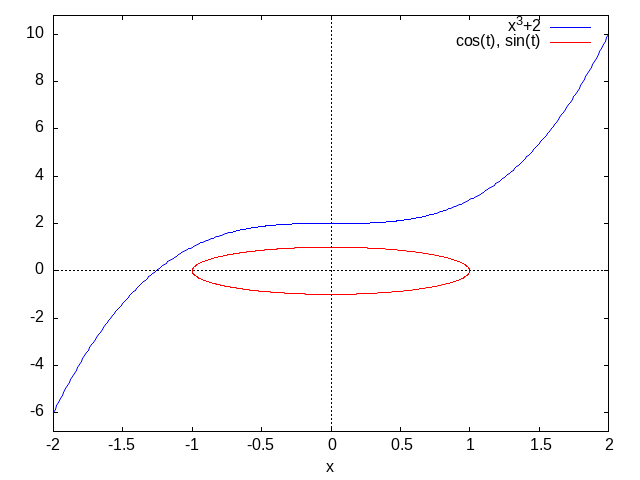
図20.13. Max-ref-3_files/fig20-3.png
◆ 実行例:リストデータの作図
/home/inoue/bin/go tmp_lang/chunk-4.mx > tmp_lang/chunk-4.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-4.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-4.mx
"/* 注:リストデータの作図*/"
xx:[10,20,30,40,50]
yy:[0.6,0.9,1.1,1.3,1.4]
xy:[[10,0.6],[20,0.9],[30,1.1],[40,1.3],[50,1.4]]
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d1.png"])
plot2d([discrete,xx,yy])
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d2.png"])
plot2d([discrete,xy],[style,points])
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d3.png"])
plot2d([[discrete,xy],2*%pi*sqrt(l/980)],[l,0,50],
[style,[points,3,5],[lines,1,3]],[legend,"experiment","theory"],
[xlabel,"pendulum's length (cm)"],[ylabel,"period (s)"])
/var/www/html/LANG/tmp_lang/chunk-4.mx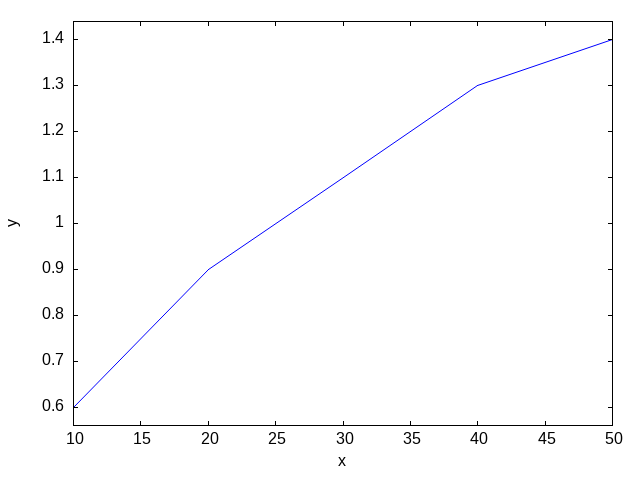
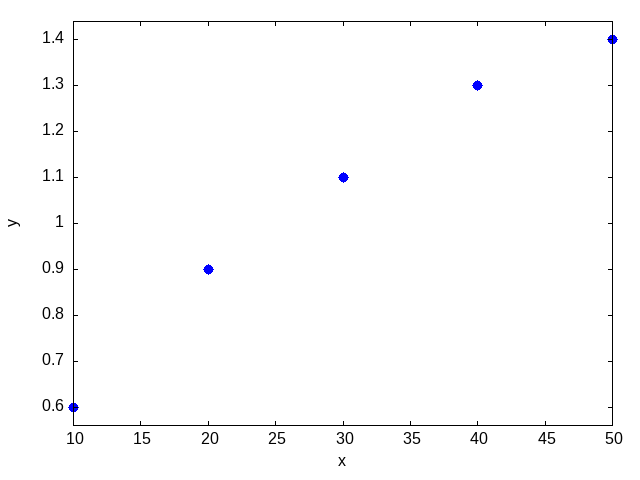
図20.14. Max-ref-3_files/fig20-d1.png fig20-d2.png
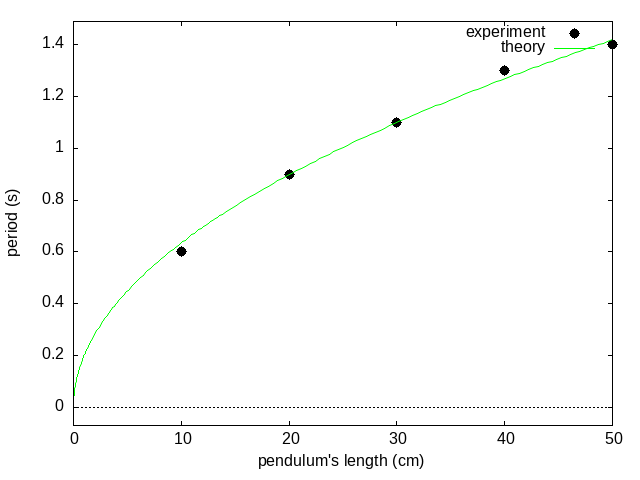
図20.15. Max-ref-3_files/fig20-d3.png
20.1.2 3次元プロット(plot3d)
● plot3d(exp,xrange,yrange,…,options,..)
● plot3d([exp_1,exp_2,exp_3],xrange,yrange,…,options,..)
◆ 実行例:2変数関数 \(z = f(u,\,v)\) の表示
/home/inoue/bin/go tmp_lang/chunk-5.mx > tmp_lang/chunk-5.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-5.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-5.mx
display2d:false
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-4.png"])
plot3d(2^((-u^2)+v^2),[u,-5,5],[v,-7,7])
set pm3d hidden3d 100 border lw 0.5 lt rgb "#000000"
^
"/tmp/maxout35622.gnuplot" line 9: invalid pm3d option
"/var/www/html/LANG/tmp_lang/chunk-5.mx"
図20.16. Max-ref-3_files/fig20-4.png
変数 u と v の領域を各々 [-5,5] と [-7,7], u を x 軸, v を y 軸として, \(z = 2^{( - u^2 + v^2 )}\) のグラフを表示している.
◆ 実行例:2変数関数 \(z = f(x(y),\,y(t))\) の表示
/home/inoue/bin/go tmp_lang/chunk-6.mx > tmp_lang/chunk-6.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-6.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-6.mx
display2d:false
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-5.png"])
plot3d([cos(x)*(3+y*cos(x/2)),sin(x)*(3+y*cos(x/2)),y*sin(x/2)],[x,-%pi,%pi],
[y,-1,1],['grid,50,15])
set pm3d hidden3d 100 border lw 0.5 lt rgb "#000000"
^
"/tmp/maxout35659.gnuplot" line 9: invalid pm3d option
"/var/www/html/LANG/tmp_lang/chunk-6.mx"
図20.17. Max-ref-3_files/fig20-5.png
この例では, これはメビウスの輪を表示し, plot3d
の最初の引数で与えられた 3 個の
式でパラメータ付けられている. 最後のオプションの [’grid, 50, 15]
は x と y 方向の長方形の刻み数を与える.
等高線図の作図
/home/inoue/bin/go tmp_lang/chunk-7.mx > tmp_lang/chunk-7.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-7.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-7.mx
display2d:false
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d4.png"])
contour_plot(x^2+y^2,[x,-4,4],[y,-4,4])
contour_plot is now obsolete. Using plot2d instead:
plot2d ([contour, y^2+x^2], [x,-4,4], [y,-4,4])
f(x,y):=x^2+y^2
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d5.png"])
contour_plot(f(x,y),[x,-4,4],[y,-4,4],[gnuplot_preamble,"set size ratio -1"])
contour_plot is now obsolete. Using plot2d instead:
plot2d ([contour, y^2+x^2], [x,-4,4], [y,-4,4], [gnuplot_preamble,"set size ratio -1"])
set_plot_option(['gnuplot_out_file,"Max-ref-3_files/fig20-d6.png"])
contour_plot(f(x,y),[x,-4,4],[y,-4,4],
[gnuplot_preamble,"set size ratio -1; set cntrparam level 12"])
contour_plot is now obsolete. Using plot2d instead:
plot2d ([contour, y^2+x^2], [x,-4,4], [y,-4,4], [gnuplot_preamble,"set size ratio -1; set cntrparam level 12"])
"/var/www/html/LANG/tmp_lang/chunk-7.mx"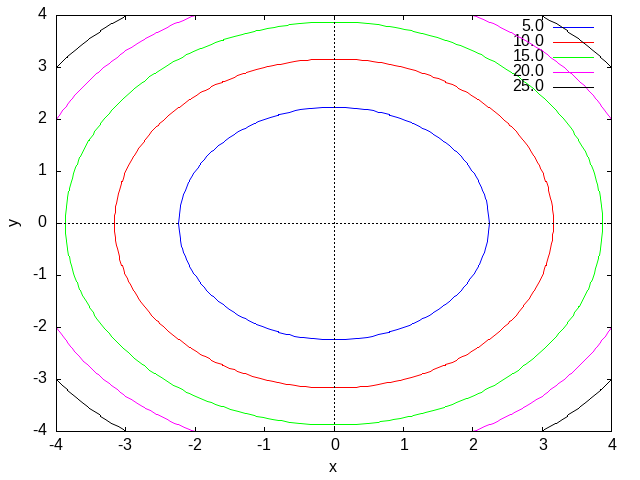
図20.18. Max-ref-3_files/fig20-d4.png
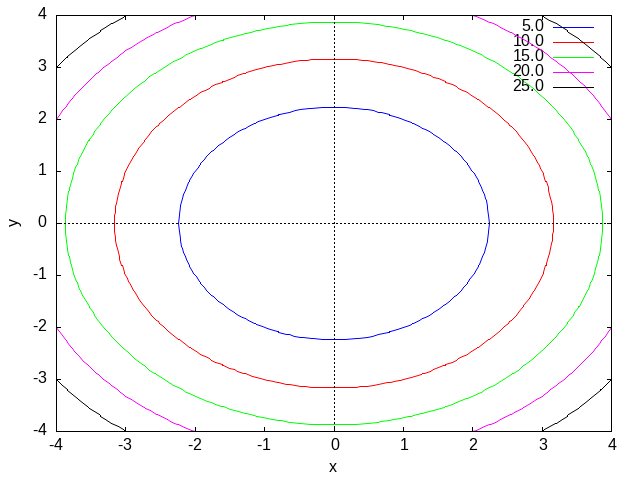

図20.19. Max-ref-3_files/fig20-d1.png fig20-d5,d6.png
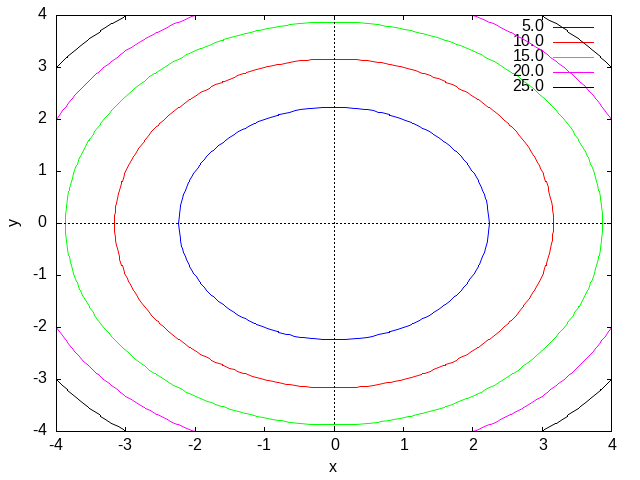
図20.19. Max-ref-3_files/fig20-d5,d6.png
20.2 作図オプション
(%i1) plot_options;
(%o1) [[x, - 1.75555970201398E+305, 1.75555970201398E+305],
[y, - 1.75555970201398E+305, 1.75555970201398E+305], [t, - 3, 3],
[grid, 30, 30], [view_direction, 1, 1, 1], [colour_z, false],
[transform_xy, false], [run_viewer, true], [plot_format, gnuplot],
[gnuplot_term, png], [gnuplot_out_file, false], [nticks, 10],
[adapt_depth, 10], [gnuplot_pm3d, false], [gnuplot_preamble, ],
[gnuplot_curve_titles, [default]], [gnuplot_curve_styles,
[with lines 3, with lines 1, with lines 2, with lines 5, with lines 4,
with lines 6, with lines 7]], [gnuplot_default_term_command, ],
[gnuplot_dumb_term_command, set term dumb 79 22],
[gnuplot_ps_term_command,
set size 1.5, 1.5;set term postscript eps enhanced color solid 24],
[logx, false], [logy, false], [plot_realpart, false]]
(%i2)設定変更は,set_plot_options(項目,値) で行う.ただし,指定でき る項目は1項目づつ行う必要がある.または,描画関数の中で指定する.
1) set_plot_options(['plot_format, gnuplot])$
set_plot_options(['run_viewer, false])$
plot2d(sin(x),[x,0,4])$
2) plot2d(sin(x),[x,0,4],['plot_format, gnuplot],[run_viewer, false])$作図関数 plot2d, plot3d では, plot_format で指定したアプリケーション向けのデータファイルを, ユーザのホームディレクトリ上に,maxout.gnuplot, maxout.openmath のように作成する. run_view が true の場合は,上記データファイルを外部アプリケーションに渡す.
☆☆☆ plot_options の一般的項目
◎ [plot_format, gnuplot]
グラフ表示アプリケーションを指定する.指定できるアプリケーションとしては,gnuplot,
openmath, geomview, ps, mgnuplot と zic がある.ps
を指定した場合は,外部アプリケーション gv (ghostview) が起動する.
◎ [run_viewer, true]
true の場合,plot_format で指定したアプリケーションを起動する.
◎ [colour_z, false]
カラーのPSファイルを出力するか否かを指定する.[plot_format, ps]
を指定したときのみ有効となる.
◎ [view_direction, 1, 1, 1]
plot_format が ps の場合に3次元グラフの視点を指定する.[plot_format,
ps] を指定したときのみ有効となる.
◎ [transform_xy, false]
3次元グラフ表示で座標変換を行うか否かを指定する.
◎ [grid, 30, 30]
3次元グラフの解像度を指定する. ◎ [nticks, 10]
2次元グラフの解像度を指定する.
◎ [logx, false]
2次元グラフで横軸を対数目盛にするか否かを指定する.
◎ [logy, false]
2次元グラフで縦軸を対数目盛にするか否かを指定する.
◎ [plot_realpart, false]
複素関数のとき,実部の表示を行うか否かを指定する. plot2d (log(x), [x,
-5, 5], [plot_realpart, true]); のように用いる.
◎ [x, - 1.75555970201398E+305, 1.75555970201398E+305]
横軸の表示可能な区間を指定する.
◎ [y, - 1.75555970201398E+305, 1.75555970201398E+305]
縦軸の表示可能な区間を指定する. ◎ [t, - 3, 3]
助変数表示に置ける表示可能な区間を指定する.
◎ [adapt_depth, 10]
光点の間隔を指定する.
☆☆☆ gnuplot における plot_options の項目
◎ [gnuplot_pm3d, false]
gnuplot の PM3D(曲面張り処理)を行うか否かを指定する.
◎ [gnuplot_curve_titles, [default]] (廃止)
描画する曲線の表題を指定する.[legend, “line1”, “line2”]
を用いる.set_plot_option では指定できず,plot2d
の中で指定する.以下に例を示す.
◎ [gnuplot_curve_styles, [“with lines 3”, “with lines 1”, …]]
(廃止)
描画する曲線の様式を文字列で指定する. [style, [lines, w, t], [points,
w, t]] を用いる. w は線幅を指定し,t は線種(色)を指定する.
set_plot_option では指定できず,plot2d の中で指定する.
(1) 凡例位置を変更する
set_plot_option(['gnuplot_preamble, "set key right bottom;"])$
(2) 格子線を入れる
set_plot_option(['gnuplot_preamble, "set grid on;"])$
(3) 縦軸の描画区間を指定する.
set_plot_option(['gnuplot_preamble, "set yrange [ymin:ymax];"])$
(4) 原点をとおる座標を入れる.
set_plot_option(['gnuplot_preamble, "set zeroaxis;"])$
(5) plot3d において,面付け処理,底面への投影とワイヤ線の消去を指定する.
set_plot_option(['gnuplot_preamble, "set pm3d at bs; unset surf"])$なお,線種の指定は,lines の他に, points, linespoints, impulses,
dots 等がある.詳細は GNUPLOT マニュアルを参照. ◎ [gnuplot_out_file,
false]
gnuplot 出力ファイルを指定する.
◎ [gnuplot_term, ps]
gnuplot のターミナルタイプを指定する.
◎ [gnuplot_default_term_command, ]
gnuplot の指定したターミナルタイプ上での追加指定を与える.
◎ [gnuplot_dumb_term_command, set term dumb 79 22]
gnuplot の指定したターミナルタイプが dump
のときの追加指定を与える.
◎ [gnuplot_ps_term_command,
set size 1.5, 1.5;set term postscript eps enhanced color solid 24]
PS ファイルに追加する命令を指定する.ここで,set size は画面サイズ,24
は文字サイズを指定する. (白黒の場合は color を mono に変更する.) ◎
[xlabel, “x-axis” ] (plot2d の中で指定する.)
◎ [ylabel, “y-axis” ] (plot2d の中で指定する.)
◎ [gnuplot_preamble, ]
gnuplot に引き渡す藷設定を文字列で指定する.以下に例を示す.
20.3 作図例
標準の作図例
/home/inoue/bin/go tmp_lang/chunk-8.mx > tmp_lang/chunk-8.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-8.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-8.mx
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g0.png"])
plot2d(sin(x),[x,(-2)*%pi,2*%pi])
/var/www/html/LANG/tmp_lang/chunk-8.mx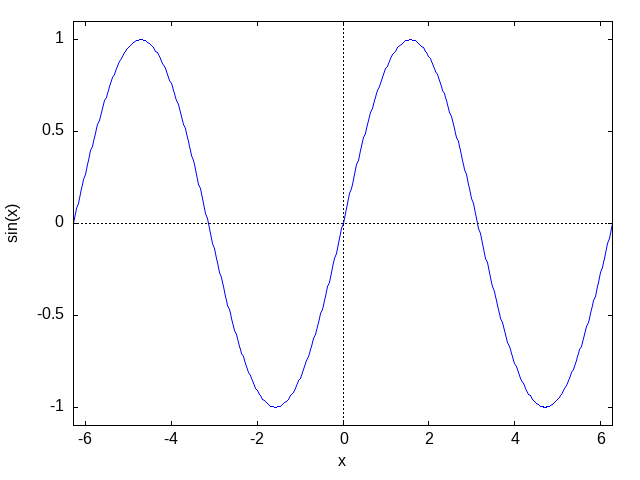
図20.g0. Max-ref-3_files/fig20-g0.png
描画範囲,原点座標,文字サイズの指定例
/home/inoue/bin/go tmp_lang/chunk-9.mx > tmp_lang/chunk-9.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-9.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-9.mx
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g1a.png"])
gpreamble:"set yrange [-1.1:1.1]; set zeroaxis linetype 7;"
plot2d(sin(x),[x,(-2)*%pi,2*%pi],['gnuplot_preamble,gpreamble])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g1b.png"])
gpreamble:sconcat("set xtics ('-2{/Symbol p}' -6.283, '-3{/Symbol p}/2' -4.712,",
"'-{/Symbol p}' -3.142, '-{/Symbol p}/2' -1.571,","'0' 0,",
"'{/Symbol p}/2' 1.571, '{/Symbol p}' 3.142,",
"'3{/Symbol p}/2' 4.712, '2{/Symbol p}' 6.283);",
"set yrange [-1.1:1.1];","set key right top;",
"set zeroaxis linetype 7; ")
plot2d([sin(x),cos(x)],[x,(-2)*%pi,2*%pi],['legend,"Sin(x)","Cos(x)"],
['gnuplot_preamble,gpreamble])
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
gdImageStringFT: fontconfig: Didn't find expected font family. Perhaps URW Type 1 fonts need installing? while printing string p with font Symbol
/var/www/html/LANG/tmp_lang/chunk-9.mx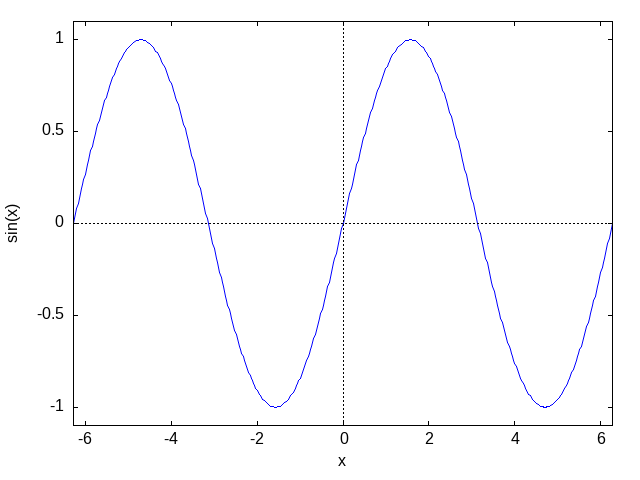
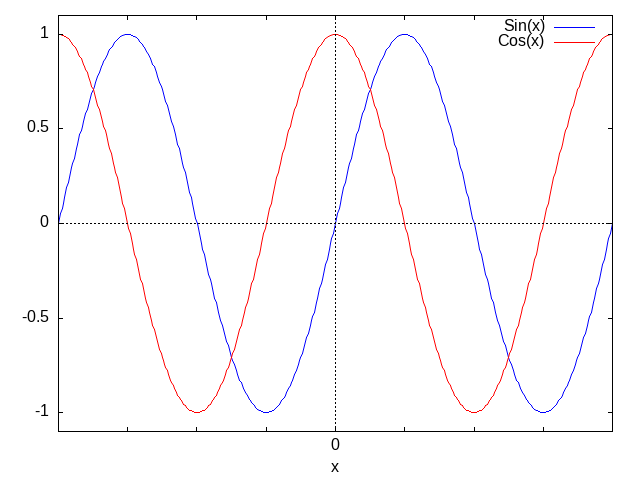
図20.g1. Max-ref-3_files/fig20-g1.png
[作図オプション例]
gpreamble : sconcat("set title ''; ",
"set xlabel 'x'; ",
"set ylabel ''; ",
"set yrange [0:0.4]; ");
plot2d(f(x),[x,-3,3],[gnuplot_preamble, gpreamble]);
/* 横軸の設定例 */
gpreamble : sconcat(
"set xtics ('-2{/Symbol p}' -6.283, '-3{/Symbol p}/2' -4.712,",
"'-{/Symbol p}' -3.142, '-{/Symbol p}/2' -1.571,",
"'0' 0,",
"'{/Symbol p}/2' 1.571, '{/Symbol p}' 3.142,",
"'3{/Symbol p}/2' 4.712, '2{/Symbol p}' 6.283);",
"set yrange [-1.5:1.5];",
"set key right top;",
"set zeroaxis; "
)$
plot2d([sin(x),cos(x)],[x,-2*%pi,2*%pi], [gnuplot_preamble, gpreamble])$媒介変数表示の例
/home/inoue/bin/go tmp_lang/chunk-10.mx > tmp_lang/chunk-10.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-10.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-10.mx
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g1c.png"])
gpreamble:sconcat("set xrange [-1.1:1.1]; "," set yrange [-1.1:1.1]; ",
" set zeroaxis linetype 7;")
plot2d([parametric,cos(t),sin(t),[t,0,2*%pi]],['gnuplot_preamble,gpreamble])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g1d.png"])
plot2d([parametric,cos(t),sin(t),[t,0,2*%pi]],['nticks,100],
['gnuplot_preamble,gpreamble])
/var/www/html/LANG/tmp_lang/chunk-10.mx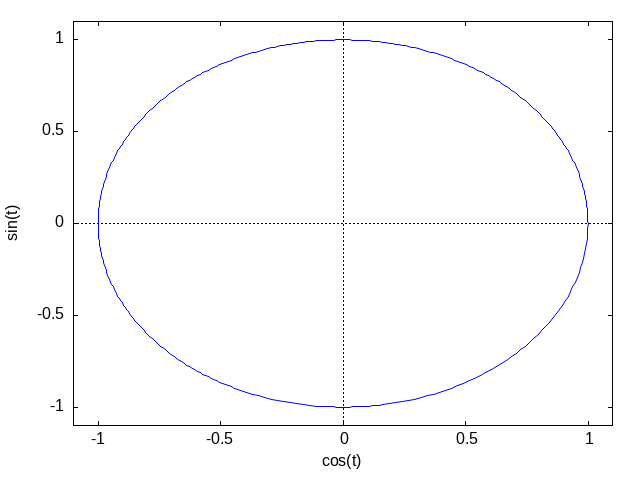
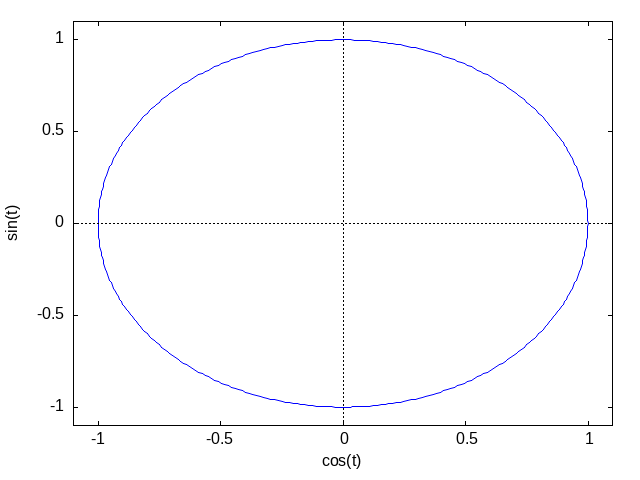
図20.g. Max-ref-3_files/fig20-g1c,d.png
リストプロットの例
/home/inoue/bin/go tmp_lang/chunk-11.mx > tmp_lang/chunk-11.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-11.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-11.mx
display2d:false
(xmin:-3,xmax:3,n:50)
x[i]:=float(xmin+((xmax-xmin)*i)/n)
xl:makelist(x[i],i,0,n)
yl:makelist(float(erf(x)),x,xl)
plot2d([discrete,xl,yl],['ylabel,""],
['gnuplot_preamble,"set zeroaxis linetype 7; set yrange [-1.1:1.1]"],
['gnuplot_out_file,"Max-ref-3_files/fig20-d1.png"])
"/var/www/html/LANG/tmp_lang/chunk-11.mx"
図20.g. Max-ref-3_files/fig20-d1.png
曲面の表示例
/home/inoue/bin/go tmp_lang/chunk-12.mx > tmp_lang/chunk-12.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-12.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-12.mx
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g1.png"])
plot3d(sin(x*y),[x,-3,3],[y,-3,3],[gnuplot_pm3d,true],[grid,50,40])
set pm3d hidden3d 100 border lw 0.5 lt rgb "#000000"
^
"/tmp/maxout35889.gnuplot" line 9: invalid pm3d option
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-g2.png"])
plot3d(sin(x*y),[x,-3,3],[y,-3,3],
[gnuplot_preamble,"set pm3d at bs; unset surf"],[grid,50,40])
set pm3d hidden3d 100 border lw 0.5 lt rgb "#000000"
^
"/tmp/maxout35889.gnuplot" line 10: invalid pm3d option
/var/www/html/LANG/tmp_lang/chunk-12.mx

図20.g. Max-ref-3_files/fig20-g1,g2.png
/home/inoue/bin/go tmp_lang/chunk-13.mx > tmp_lang/chunk-13.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-13.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-13.mx
batchload("/home/inoue/.maxima/max-init.mac")
file_search1: /home/inoue/.maxima/max-init.mac not found in file_search_maxima.
-- an error. To debug this try: debugmode(true);
/var/www/html/LANG/tmp_lang/chunk-13.mx
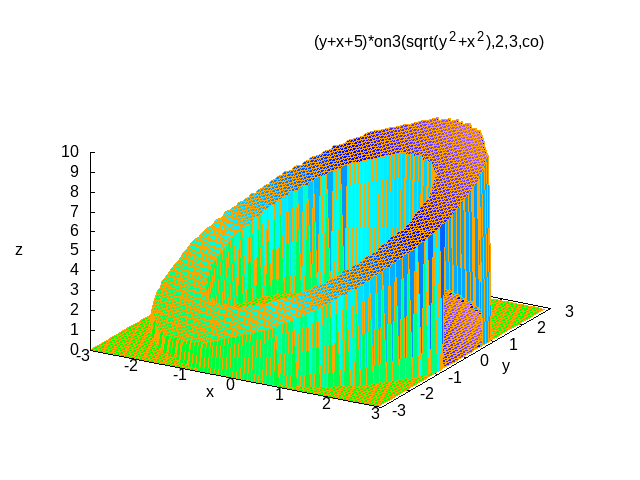
図20.g. Max-ref-3_files/fig20-g1,g2.png
等高線図への応用例
/home/inoue/bin/go tmp_lang/chunk-14.mx > tmp_lang/chunk-14.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-14.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-14.mx
display2d:false
set_plot_option([plot_format,gnuplot])
set_plot_option([gnuplot_term,png])
set_plot_option([gnuplot_out_file,"Max-ref-3_files/fig20-ga.png"])
plot3d(cos((-x^2)+y^3/4),[x,-4,4],[y,-4,4],
[gnuplot_preamble,"set view map; unset surface"],[gnuplot_pm3d,true],
[grid,150,150])
set pm3d hidden3d 100 border lw 0.5 lt rgb "#000000"
^
"/tmp/maxout35970.gnuplot" line 10: invalid pm3d option
"/var/www/html/LANG/tmp_lang/chunk-14.mx"
図20.ga. Max-ref-3_files/fig20-ga.png
21 作図2 draw
maxima draw 例
draw2d( terminal='png, file_name="Max-ref-3_files/draw-1",
title="Two simple plots",
xlabel="x",ylabel="y",grid=true,
color=red,key="A sinus",
explicit(sin(x),x,1,10),
color=blue,line_type=dots,key="A cosinus",
explicit(cos(x),x,1,10)
)$## /home/inoue/bin/go tmp_lang/chunk-15.mx > tmp_lang/chunk-15.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-15.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-15.mx
## draw2d(terminal = 'png,file_name = "Max-ref-3_files/draw-1",
## title = "Two simple plots",xlabel = "x",ylabel = "y",grid = true,
## color = red,key = "A sinus",explicit(sin(x),x,1,10),color = blue,
## line_type = dots,key = "A cosinus",explicit(cos(x),x,1,10))
## /var/www/html/LANG/tmp_lang/chunk-15.mx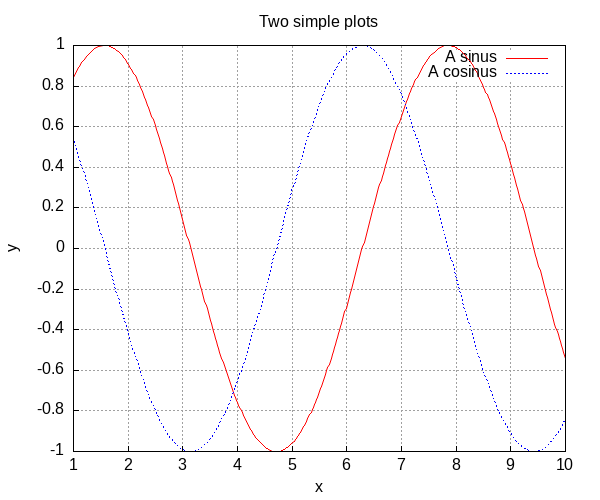
maxima gr2d 例
◆ 実行例1:
/home/inoue/bin/go tmp_lang/chunk-16.mxl > tmp_lang/chunk-16.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-16.mxl")
read and interpret /var/www/html/LANG/tmp_lang/chunk-16.mxl
display2d:false
" /* F(x) = erf(x) の場合 */ "
define(F(x),erf(x))
define(f(x),diff(F(x),x))
Maxima encountered a Lisp error:
Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
Automatically continuing.
To enable the Lisp debugger set *debugger-hook* to nil.
c0show(f(x))
f(x) = f(x)
g01:gr2d(key = "f(x)",explicit(f(x),x,-4,4),grid = true,title = "f(x)=dF(x)/dx")
g02:gr2d(key = "F(x)",explicit(F(x),x,-4,4),grid = true,title = "F(x)=erf(x)")
draw(g01,g02,columns = 2,dimensions = [800,300],'terminal = 'png,
'file_name = "Max-ref-2_files/fig11-3")
draw2d (explicit): non defined variable in term: 'realpart(f(-3.7241379))
-- an error. To debug this try: debugmode(true);
"/var/www/html/LANG/tmp_lang/chunk-16.mxl"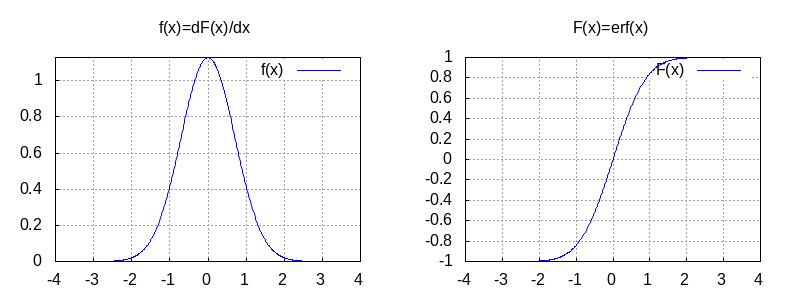
Graph of erf(x) 誤差関数
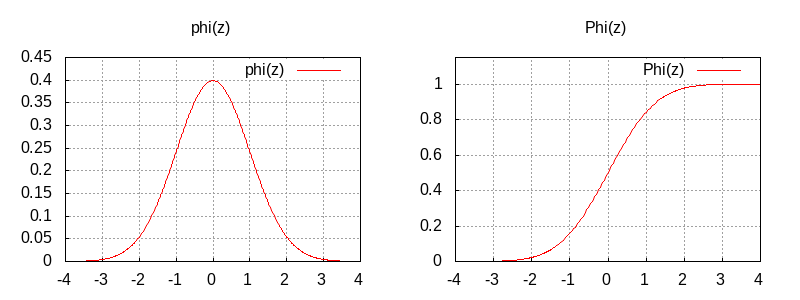
Graph of Phi(x) 標準正規分布の分布関数
g1: gr2d(title="Ellipse",
nticks=300,
parametric(2*cos(t),5*sin(t),t,0,2*%pi))$
g2: gr2d(title="Triangle",
polygon([4,5,7],[6,4,2]))$
draw( terminal='png, file_name="Max-ref-3_files/tmp1",
g1, g2, columns = 2, dimensions=[800,400])$## /home/inoue/bin/go tmp_lang/chunk-17.mx > tmp_lang/chunk-17.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-17.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-17.mx
## g1:gr2d(title = "Ellipse",nticks = 300,
## parametric(2*cos(t),5*sin(t),t,0,2*%pi))
## g2:gr2d(title = "Triangle",polygon([4,5,7],[6,4,2]))
## draw(terminal = 'png,file_name = "Max-ref-3_files/tmp1",g1,g2,columns = 2,
## dimensions = [800,400])
## /var/www/html/LANG/tmp_lang/chunk-17.mx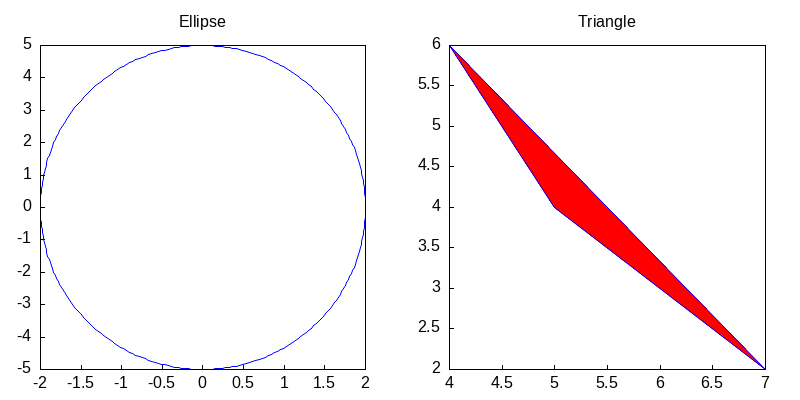
maxima gr3d 例
g1 : gr3d(explicit(x^2+y^2,x,-1,1,y,-1,1))$
draw( terminal='png, file_name="Max-ref-3_files/tmp3", g1)$## /home/inoue/bin/go tmp_lang/chunk-18.mx > tmp_lang/chunk-18.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-18.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-18.mx
## g1:gr3d(explicit(x^2+y^2,x,-1,1,y,-1,1))
## draw(terminal = 'png,file_name = "Max-ref-3_files/tmp3",g1)
## /var/www/html/LANG/tmp_lang/chunk-18.mx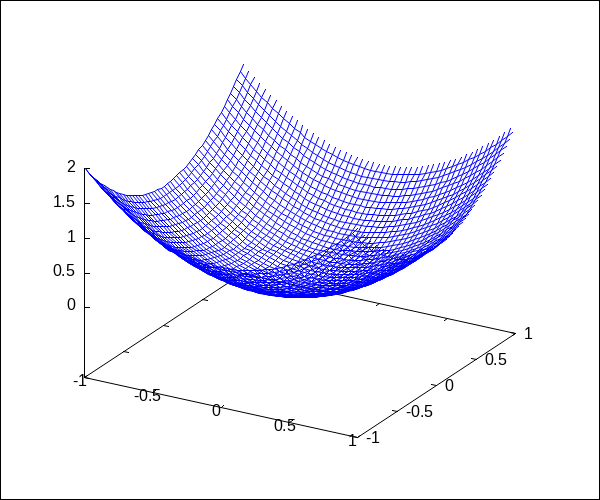
maxima gr3d + gif アニメーション例
draw(
delay = 100,
file_name = "Max-ref-3_files/zzz",
terminal = 'animated_gif,
gr2d(explicit(x^2,x,-1,1)),
gr2d(explicit(x^3,x,-1,1)),
gr2d(explicit(x^4,x,-1,1)));## /home/inoue/bin/go tmp_lang/chunk-19.mx > tmp_lang/chunk-19.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-19.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-19.mx
## draw(delay = 100,file_name = "Max-ref-3_files/zzz",terminal = 'animated_gif,
## gr2d(explicit(x^2,x,-1,1)),gr2d(explicit(x^3,x,-1,1)),
## gr2d(explicit(x^4,x,-1,1)))
## 3 frames in animation sequence
## [gr2d(explicit), gr2d(explicit), gr2d(explicit)]
## /var/www/html/LANG/tmp_lang/chunk-19.mx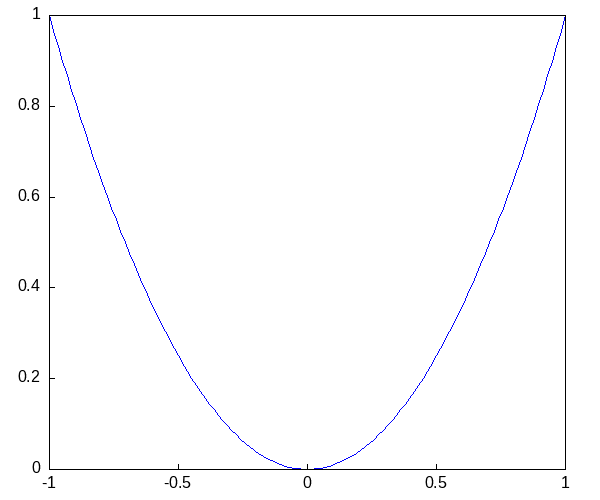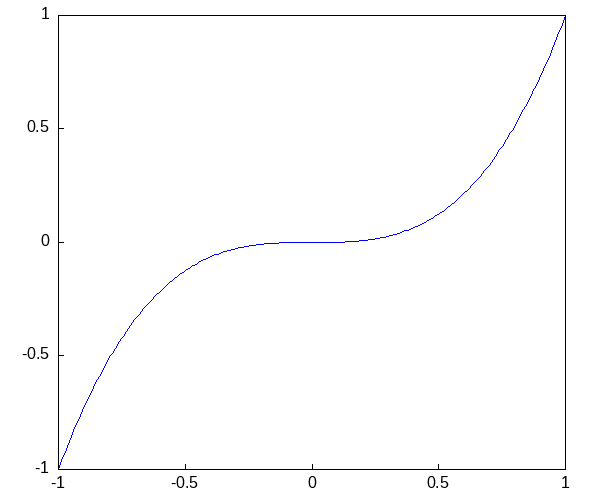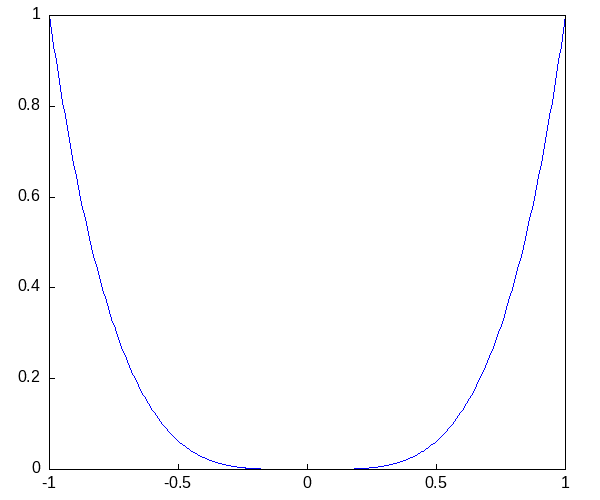
maxima multi line plot (multiplotは機能せず!!)
set_draw_defaults(
xrange = [-1.1,1.1],
yrange = [-1,1],
grid = true,
title = "Multi Lines plot" )$
/* multiplotは機能せず
multiplot_mode(aquaterm)$
draw2d(color=blue, explicit(x^2,x,-1,1))$
draw2d(color=red, explicit(x^3,x,-1,1))$
draw2d(color=brown, explicit(x^4,x,-1,1))$
multiplot_mode(none)$
*/
g : gr2d(color=blue, explicit(x^2,x,-1,1),
color=red, explicit(x^3,x,-1,1),
color=brown, explicit(x^4,x,-1,1))$
draw(g, terminal='png, file_name="Max-ref-3_files/tmp4")$## /home/inoue/bin/go tmp_lang/chunk-20.mx > tmp_lang/chunk-20.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-20.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-20.mx
## set_draw_defaults(xrange = [-1.1,1.1],yrange = [-1,1],grid = true,
## title = "Multi Lines plot")
## g:gr2d(color = blue,explicit(x^2,x,-1,1),color = red,explicit(x^3,x,-1,1),
## color = brown,explicit(x^4,x,-1,1))
## draw(g,terminal = 'png,file_name = "Max-ref-3_files/tmp4")
## /var/www/html/LANG/tmp_lang/chunk-20.mx
maxima gr3d カラー
/**
g : gr3d(enhanced3d = true,
color = green,
cbrange = [-3,10],
explicit(x^2+y^2, x,-2,2,y,-2,2)) $
draw(g, terminal='png, file_name="Max-ref-3_files/tmp5")
*/
draw3d (terminal='png, file_name="Max-ref-3_files/tmp5",
enhanced3d = true,
color = green,
cbrange = [-3,10],
explicit(x^2+y^2, x,-2,2,y,-2,2)) $## /home/inoue/bin/go tmp_lang/chunk-21.mx > tmp_lang/chunk-21.out 2>&1
## batch("/var/www/html/LANG/tmp_lang/chunk-21.mx")
## read and interpret /var/www/html/LANG/tmp_lang/chunk-21.mx
## draw3d(terminal = 'png,file_name = "Max-ref-3_files/tmp5",enhanced3d = true,
## color = green,cbrange = [-3,10],explicit(x^2+y^2,x,-2,2,y,-2,2))
## /var/www/html/LANG/tmp_lang/chunk-21.mx
21.1 draw メモ
******* Maxima (数式電卓): draw **********
draw2d(color=red, key="sin(x)", explicit(sin(x)/x,x,-10,10));
draw2d(xrange=[-20,20],explicit(sin(x)/x,x,-10,10));
(%i4) neko:explicit(sin(x)/x,x,-10,10); sin(x)
(%i5) X1:xrange=[-20,20];
(%i6) Y1:yrange=[-0.5,1.5];
(%i7) draw2d(X1,neko,Y1);
(%i28) nekoneko:points([1,2,3],[1,2,3]);
(%o28) points([1, 2, 3], [1, 2, 3]);
(%i29) draw2d(xrange=[-1,6], yrange=[-1,6], nekoneko, point_size=3,
point_type=diamant, points_joined=true, line_type=dots,
color=red, nekoneko);
(%o29) [gr2d(points, points)]
draw函数とdraw2d函数,draw3d函数との関係
draw2d(対象1, ... , 対象n) draw3d(対象1, ... ,対象n)
⇒ ⇒ draw(gr2d(対象1, ... , 対象n)) draw(gr3d(対象1, ... , 対象n))
(%i7) draw(gr2d(explicit(sin(x),x,-10,10)), gr2d(explicit(x^2+1,x,-2,2)));
(%i15) draw(columns=1,gr2d(explicit(sin(x),x,-10,10)),
gr3d(explicit(x*y,x,-2,2,y,-2,2)),
(%i16) draw(columns=3,gr2d(explicit(sin(x),x,-10,10)),
gr3d(explicit(x*y,x,-2,2,y,-2,2)),
gr2d(explicit(x^2-x+1,x,-2,2)));
===============================================================================
◎ drawの大域的属性
columns=1 terminal={eps|wxt|png} pic width=640 pic height=480
eps_width=12 eps_height=8 file_name=\"maxima_out\"
◎ グラフ枠に関連する属性
xrange=[xl,xr] yrange=[yl,yr] zrange=[zl,zr]
axis_top=true axis_bottom=true axis_right=true axis_left=true axis_3d=true
◎ 軸の目盛とグリッド(網線)の属性
grid=true, xtics=true ytics=true ztics=true logx=false logy=false logz=false grid=false
◎ 表題や各軸のラベルに関連する属性
title="Titile", xlabel="x", ylabel="y", zlabel="z"
◎ 視点の変更, 検出した座標値の保存に関連する属性
rot_vertical=60, rot_horizontal=30, xy_file=\"\"
-------------------------------------------------------------------------------
◎ 関数
explicit(exp, x, xl, xr) <--- y=f(x)
adapt_depth=10, nticks=30, line_width=1, line_type={solid|dots},
color=black, filled_func=false, fill_color=red, key=\"\"
explicit(exp, x, xl, xr, y, yl, yr) <--- z=f(x,y)
xu_grid=30, yv_grid=30, contour={surface|base|both|map},
contour_levels=5, enhanced3d=\"\",
line_width=1, line_type={solid|dots}, color=black, key=\"\"
◎ 陰関数
implicit(exp, x, xl, xr, y, yl, yr) <--- f(x,y)=0
implicit(exp, x, xl, xr, y, yl, yr, z, zl, zr) <--- f(x,y,z)=0
ip_grid=[50,50], ip_grid_in=[5,5],
x_voxel=10, y_voxel=10, z_voxel=10,
line_width=1, line_type={solid|dots}, color=black, key=\"\"
◎ 媒介変数表示
parametric(x(t), y(t), t, tl, tr)
parametric(x(t), y(t), z(t), t, tl, tr) <---
nticks=30, line_width=1, line_type={solid|dots}, color=black, key=\"\"
◎ 極座標表示
polar(r(t),t,tmin,tmax)
nticks=30, line_width=1, line_type={solid|dots}, color=black, key=\"\"
◎ 媒介変数表示された空間曲面
parametric_surface(x(t,u),y(t,u),z(t,u), t,tl,tr, u,ul,ur)
xu_grid=30, yv_grid=30, line_width=1, line_type={solid|dots}, color=black, key=\"\"
<div style="text-align:right; color:blue">
[ PageTop](#PageTop)
[ PageEnd](#PageEnd)
[ ChapTop](#Chap-21)
[ ChapEnd](#Chap-21)
</div>
◎ 点列の描画
points(List)
List : [[x1, y1], ... , [xn, yn]] or [[x1, ... , xn], [y1, ... , yn]]
List : [[x1, y1, z1], ... , [xn, yn, zn]] or
[[x1, ... , xn], [y1, ... , yn], [z1, ... , zn]]
point_size=, point_type=, points_joined=false, line_width=,
line_type={solid,dots}, color=black, key=\"\"
point_type=x -1:none, 0:dot, 1:plus, 2:multiply 3:asterisk, 4:square
5:full_square, 6:circle, 7:filled_circle, 8:up_triabgle, 9:filled_up_triangle,
10:down_triangle, 11:filled_down_triabgle, 12:diamant, 13:filled_diamant
◎ 平面上の多角形の描画
polygon(List)
List : [[x1, y1], ... , [xn, yn]] or [[x1, ... , xn], [y1, ..., yn]]
rectangle([x1, y1], [x2, y2]) <--- 長方形の対角線上の点を指定
transparent=false (透明化の有無), border=true, fill_color=red, line_width=1,
line_type={dots|solid}, color=black, key=\"\"
◎ 楕円の描画
ellipse(原点x, 原点y, 半径1, 半径2, 角度1, 角度2 )
nticks=30, transparent=false, border=true, fill_color=red,
line_width=1, line_type=solid, color=black, key=\"\"
◎ 矢印(ベクトル)の描画
vector([基点のx座標, 基点のy座標], [基点からのx成分の増分, 基点からのy成分の増分])
vector([基点のx座標, 基点のy座標, 基点のz座標],
[基点からのx成分の増分, 基点からのy成分の増分, 基点からのZ成分の増分])
head_angle=45, head_both=false, head_length=2
head_type={filled,empty,nofilled}, line_width=1, line_type={solid,dots},
color=black, key=\"\"
◎ 画像(イメージ)の描画
image(実数行列, x0, y0, 幅, 高さ)
image([r, g, b]の行列, x0, y0, 幅, 高さ)
colorbox=true, palette=\"\"
◎ 指定凡例(legend)を記述
label([文字列1, x1, y1], ... , [文字列n, xn, yn])
label([文字列1, x1, y1, z1], ... , [文字列n, xn, yn, zn])
label_allgnment={center,left,right}
label_orientation={horizontal,vertical}
◎ その他の函数
add_zeroes(整数)
T:title=sconcat(\"f(x)=\",f(x))$ K:key=sconcat(\"f(x)=\",f(x))$
draw(font_size=12,gr2d(T,K,explicit(sin(x),x,-10,10)))$
---> font_size は maxima-5.19以降で可
*******************************";;22. ファイルの利用
22.1 Maxima でのデータ入出力について
ここでは Maxima へのデータ入力と出力について述べる. Maxima は Common LISP で記述されているため, 基本的に入出力は LISP の入出力関数を用いたも のである. 特に Maxima は表示され ている形式と内部形式が別物のため, 結果や 式を保存したり, 逆に保存したものを読込む際には, 注意が必要になる.
ファイルに画面と同じ出力を得たければ, writefile を用いる. この writefile は LISP の dribble 関数を用いたもので, 入力と出力をそのまま 指定したファイルに保存する. ただし, writefile では指定したファイルを新 規に生成するので, 単純に既存のファイルに記録したければ, appendle 関数 を用いる. writefile と appendle で開いたファイルを閉じる場合は closele() で開いたファイルを閉じる. ただし, これらのファイルは実質的 に記録ファイルであって, Maxima でそのまま再利用は出来ない. 再利用可能 なファイルを生成するのは, save と stringout である. ここで, save は Maxima の内部表現を保存する関数で, load や loadfile を用いて Maxima に読み込む. これに対して, stringout や grind は内部形式ではなく, Maxima の入力に対応する通常の形式でデータの保存を行なう.
Maxima で C の scan 命令に似たものに, read と readonly がある. こ れらの関数は, 引数として与えた文字列を全て同一行に表示し, キーボードか らの入力を待つ. 利用者は通常の Maxima の入力と同様に式を入力する. ここで, 行末には ; か $ を付ける. すると, read の場合 は式を Maxima で評価し, readonly の場合は評価せずにそのまま受け取る. この様に, 単純なファイル操作に限定されるとは言え, 必要なものは一応揃っ ており, 足りない部分は LISP で補うことになる. ウインドウのスクロールダウ ンで入力行の後戻し (playback) が可能で, 現在の作業を失なうこともない. これは関数 e を入力することで実行ができる. 開始すべき行数を数値引 数で尋ねると, それ以外は 40 行遡ることとなる.
22.2 ファイル処理に関連する環境変数
● batchkill:false
true の場合, バッチファイルを読み込む際に kill(all) と reset()
が自動的に実行されるので, 以前のバッチファイルの影響が 全て無効になる.
batchkill が他のアトムであれば, batchkill の値で kill が実行される.
● batcount:0
ファイルからのバッチ処理された最後の式の番号を設定する.
batcon(batchcount-1) は以前の処理から, 最新の batch 処理された
式の処理結果を保存する.
● file_search_Maxima, file_search_LISP, file_search_demo
load や他の関数で,
ファイルの読込を行う際に検索されるディレクトリのリスト.
file_search_Maxima は Maxima のプログラム (末尾が, mac と mc) 向け,
file_search_LISP は LISP のプログラム (末尾 が, fas, LISP, lisp) 向け,
file_search_demo が LISP のプログラム (末尾が, dem, dm1, dm2, dm3, dmt)
向けとなっており, 各々が Maxima のリスト形式 となっている.
なお, これらの値は, src/init-cl.LISP で設定されている.
● file_string_print:true
true であれば, ファイル名は文字列, false であれば,
リストとして出力される.
● loadprint:false
ファイル読込に伴うメッセージ表示を制御する環境変数である. loadprint が
取る値は, true, loadfile, autoload, false の四種類あり, 各々,
対応が異なる.
mygnuplot(f,var,range,number_ticks):=
block([numer:true],
with_stdout("/tmp/gnu",
for x:range[1] thru range[2] step
(range[2]-range[1])/number_ticks
do (print(x,at(f,var=x)))),
system("echo \"set data style lines; set title ’",
f,"’ ;plot ’/tmp/gnu’
;pause 10 \" | gnuplot"));
(%i8) with_stdout("/tmp/out",
n:5,
for i:3 thru n do(print("factorial(",i,") gives ",i!)));
(%o8) false
(%i9) system("cat /tmp/out");
factorial( 3 ) gives 6
factorial( 4 ) gives 24
factorial( 5 ) gives 120
(%o9) 0 false
● packagefile:false
save, fassave, 或いは translate を用いてパッケージ (ファイル)
を作成する場合, packagefile:true$ と設定して,
ファイルが読み込まれる時点で必要な場所を除いた情報が Maxima の情報リスト
(例えば values, functions) に追加されることを避けたいかもしれない.
この方法でパッケージに含まれる物は, 利用者のデータを付け加えた時点で,
利用者の側では得られない. これは名前の衝突の問題を解決するものでは無
いことに注意する. この環境変数は単にパッケージファイルへの出力に影
響を与えることに注意する. なお, この変数の値を true に設定すると, Maxima
の初期化ファイルの生成でも便利である.
● with_stdout(file,stmt1,stmt2,…)
ファイルを開き, stm1, stm2,… の評価を行なう. 標準出力への任意の表
示は端末の代りにファイルに送られ, 端末側には常に false が返される.
(%i1) a:read("mikeneko");
mikeneko
diff(x^2+1,x);
(%o1) 2 x 22.3 ファイル処理に関連する関数
● appendfile(fname)
指定したファイル fname に Maxima の入出力の追加を行なう. writefile
との違いは, 同名のファイルが存在した場合, writefile
では上書きをしてしまうが, appendfile は既存のファイルの末尾に Maxima
の入出力を追加する点が異なる. なお, writefile と同様に指定したファイルは
closefile() で閉じる.
● batch(fname)
指定されたファイル fname に含まれる Maxima の命令行を逐次評価する.
ファイル はパスを含まない場合, file_search_Maxima に含まれるディレクトリ
上を検索し, 存在した場合には読込みと実行をする. ファイルの内容は基本的
に Maxima での入力行と同じもので, 行末には ; か $ を置く. 又, % と %th
を用いて入力と出力を指定することも出来る. な お, 空行, Tab や
改行コードは無視される. batch 処理ファイルは通常のテ
キストエディタで編集することもできるし, Maxima の stringout 関数で出力し
たものも使える. 深刻なエラーが生じた場合, ファイル末端に達した場合にの
み, 利用者に制御が戻される. ただし, 利用者はどの時点でも
Cntrl-g を押せば, この処理を止められる.
● batchload(fname)
指定されたファイル fname のバッチ処理を行なう. batch との違いは,
batchload
ではファイルに記述された式の入力や出力表示等を行わないことである.
● batcon(arg)
中断されたファイルのバッチ処理を再開する.
● closefile()
appendfile や writefile で開かれたファイルを閉じる. closefile は LISP の
closfile を使った関数である. この closfile
は開かれたストリームを閉じる関数になる.
● filename_merge(str_1, str_2)
文字列str_1と文字列str_2の結合を行なう. 内部的には, 先頭に #P を文
字列の先頭に付けた対象を生成するが, Maxima 上では, 単純に文字列をつな
ぎ合せた様にしか見えない. 基本的には Maxima の各種命令でファイルの検
索を行う際にパス指定のあるファイル名を生成する際に用いられる関数である.
● file_search(fname)
指定したファイル fname を file_search_LISP, file_search_Maxima と
file_search_demo に含まれるディレクトリ上で検索し, ファイル
が存在すればファイル名を返し, 存在しなければ, false を返す.
● file_type(fname)
指定したファイル fname の属性を返す. ただし,
ファイル名の末尾で判断する関数 で, 返却する値も, fasl, LISP や Maxima
を返す. なお, fasl はコンパイルされた LISP ファイルである.
● load(fname)
文字列やリストで表現されたファイル名 fname の読込みを行なう.
ディレクトリ が指定されていなければ, 最初にカレントディレクトリ,
それから file_search_Maxima, file_search_LISP や file_search_demo
といった環境変数に保存されているディレクトリを 検索し,
指定されたファイルを読込もうとする.
load はファイルが batch 処理に対応していることを見付けると, batchload を
用いる(これは, 黙って端末に出力やラベルを出力せずにファイルの batch 処
理を実行することを意味する). 他のファイルの読込を行う Maxima 命令に,
loadfile, batch と demo がある. loadfile は save で
書込んだファイルに対して動作し, batch と demo は stringout
で書込まれたり, テキストエディタで命令のリ
ストとして生成されたファイル向けである.
● loadfile(fname)
指定されたファイル fname を読込む. この関数は以前の Maxima の処理で save
関数で保存した値を Maxima に戻すことに使える. ここで, パスの指定はオペ
レーティングシステムのパスの指定方法に従う. 例えば, unix の 場合 は
/home/user ディレクトリにある foo.mc ファイルを読込むのであ れば,
“/home/user/foo.mc” となる. なお. save 関数で保存したファ イルを
loadfile で読込むと, Maxima[は初期化されるので注意が必要である.
● read(str_1,…)
この関数は画面上に全ての引数を表示して入力を待つ. 利用者が式を入力
すると, 入力した式は Maxima に引渡されて評価が行なわれる.
(%i46) a:readonly("mikeneko");
mikeneko
diff(x^2+1,x);
2
(%o46) diff(x + 1, x) この例では, mikeneko と表示された後に, diff(x^2+1,x); を 入力する. ここでの入力でも通常の入力と同様に行末に ; か $ が必要である. この例では, 入力した値が Maxima に評価されて, 結局, a に 2*x が割当てられている.
● readonly(str_1, … )
引数を全て表示して, それから式を読み込む. 基本的には read
と同様であるが, read と違うのは, 読込んだ式を評価しないことである.
(%i1) 1+2+3;
(%o1) 6
(%i2) a1:x^2+y^2+1;
2 2
(%o2) y + x + 1
(%i3) resultant(x-t,y-t^2,t);
2
(%o3) y - x
(%i4) save("test",all);
(%o4) test ● save(fname, arg_1, arg_2, …)
● save(fname, name_1=exp_1, name_2=exp_2, … )
● save(fname, [m, n])
● save(fname, values, functions, labels, … )
● save(fname, all)
指定したファイル fname に, 指定した式や関数等の値を書き込む. なお,
保存した 値は削除されずに Maxima 本体にも残っている. 引数1, 引数2, … で,
各引 数の値を保存する.
[m, n] で m 番目の入力行から n 番目の入力行の内容を保存する.
引数に環境変数 values, functions, labels 等を指定することもできる.
values, functions で利用者が設定した変数値や定義関数を全て保存する. 又,
labels を指定すると, 入出力行の内容が全て保存する. 最後に, 引数 に all
を指定すれば, Maxima の内容をファイルに保存する. この場合は, 入力や計算
結果だけではなく, Maxima の様々な設定も一緒に保存されるので,
処理した内容以上にファイルが大きなものとなるので注意が必要になる. save
関数の返却値は保存先のファイル名となる.
(%i1) loadfile("test");
(%o4) test
(%i5) %i2;
2 2
(%o5) a1 : y + x + 1
(%i6) %i1;
(%o6) 6
(%i7) %o3;
2
(%o7) y - x
(%i8) loadfile("test");
(%o4) test save 関数で保存したファイルは loadfile 関数で Maxima に再び読込むことが出 来る. ただし, loadfile を実行すると, 以前の Maxima 自体を初期化し, save 関数を実行した時点にまで戻してしまう効果があるので, 注意が必要に なる. 以下の例では最初に loadfile でファイル test を読込んでいるが, 行 ラベルは上の save で保存する場合と同じものになっていることと, 二度目に loadfile を実行するとラベルが (%i8) から (%i5) に戻って いることに注意する.
;;; -*- Mode: LISP; package:Maxima[; syntax:common-LISP; -*-
(in-package "Maxima[")
(DSKSETQ $%I1 '((MPLUS) 1 2 3))
(ADDLABEL '$%I1)
(DSKSETQ $%O1 6)
(ADDLABEL '$%O1)
(DSKSETQ $%I2 '((MSETQ) $A1 ((MPLUS) ((MEXPT) $X 2) ((MEXPT) $Y 2) 1)))
(ADDLABEL '$%I2)
(DSKSETQ $%O2 '((MPLUS SIMP) 1 ((MEXPT SIMP) $X 2) ((MEXPT SIMP) $Y 2)))
(ADDLABEL '$%O2)
(DSKSETQ $%I3
'(($RESULTANT) ((MPLUS) $X ((MMINUS) $T))
((MPLUS) $Y ((MMINUS) ((MEXPT) $T 2))) $T)) (ADDLABEL '$%I3)
(DSKSETQ $%O3
'((MPLUS SIMP) ((MTIMES SIMP) -1 ((MEXPT SIMP RATSIMP) $X 2)) $Y))
(ADDLABEL ’$%O3) (DSKSETQ $%I4
'(($SAVE) &TEST $ALL)) (ADDLABEL '$%I4)
(DSKSETQ $A1 '((MPLUS SIMP) 1 ((MEXPT SIMP) $X 2) ((MEXPT SIMP) $Y 2)))
(ADD2LNC '$A1 $VALUES)
以下略
なお, save ファイルの内容は, LISP の S 式そのものとなる. 要するに, LISP 上で動く Maxima のためのデータファイルになる. ファイルの先頭側に実 行内容の内部形式が記述されるが, その後には Maxima の諸設定が保存される. そのため, 以下に示す例は 1+2+3 から 4 行の入力だけだが, save 関数で保存したファイル (test) は 256 行に及ぶ. これは内部形式で記述す るとどうしても長くなる側面もあるが, 実際は, 入出力以外に様々な設定 (大 域変数の値等) も保存されているためである.
(%i1) writefile("test1");
(%o1) #<OUTPUT BUFFERED FILE-STREAM CHARACTER test1>
(%i2) 1+2+3;
(%o2) 6
(%i3) diff(sin(x)*x+2,x);
(%o3) sin(x) + x cos(x)
(%i4) closefile();
(%o4) #<CLOSED OUTPUT BUFFERED FILE-STREAM CHARACTER test1>
そのため, Maxima 内部でデータがどの様に処理されているかを見る場合には便 利である. とは言え, 作業を一旦中断し, 中断した個所から再度処理を行う必 要がなければ, save 以外の命令, 例えば, stringout や grind を用いた方が 総合的な使い勝手自体は良い.
● stringout(fname, exp_1, exp_2, …)
● stringout(fname, [m, n])
● stringout(fname, input)
● stringout(fname, functions)
● stringout(fname, values)
指定したファイル fname に Maxima が読込める書式で出力する. 直接, exp_1,
exp_2, … と式を並べると, 各式が順番にファイルに書込まれる. 引数に, [m,
n] と指定すると入力行の m 行から n 行がファイルの書込まれる.
これらに対し, input を指定すると入力行全てが書込まれる. functions
を指定すると環境変数 functions に記載された利用者定義の関数
が全て保存される. 同様に values を指定すると, 環境変数 values に記載
された利用者定義の変数の値が書込まれる. なお, この stringout 関数は
writefile を実行中に利用することもできる. 環境変数の grind が true で
あれば, stringout は文字列では無く, grind と同じ書式で出力する.
● writele(fname)
書込み用にファイル fname を新規に開く. writefile を実行すると,
それ以降の Maxima への入力と出力処理は全て指定したファイルに記録される.
そのため, このファイルをそのまま Maxima
に再度読込ませたりすることは出来ない. ファ イル名の指定は文字列で行なう.
文字列ではなく, ABCD の様に二重引用符 無しで指定すると, Maxima
はアトムの内部表現で用いる $ を頭に付 けたファイル名(この例では $ABCD)
でファイルを生成する. なお, こ の writefile の実体は LISP の dribble
関数 である. \ ファイルを閉じる場合は closefile() を用いる.
以下に簡単な例を示す.
;; Dribble of #<IO TERMINAL-STREAM> started 2005-11-17 06:31:16
(%o1) #<OUTPUT BUFFERED FILE-STREAM CHARACTER test1>
(%i2) 1+2+3;
(%o2) 6
(%i3) diff(sin(x)*x+2,x);
(%o3) sin(x) + x cos(x)
(%i4) closefile();
;; Dribble of #<IO TERMINAL-STREAM> finished 2005-11-17 06:31:40
f(n):=block(integrate(x ,x),subst(3,x,%%)-subst(2,x,%%))
と
f(n):=block([%%],%%:integrate(x ,x),s n n ??? この様に,Maxima の画面入出力そのままが保存されている. この writefile 関数を記録ファイルの生成に利用すれば, 下手なフロントエンドも不要になる.
23. システム
23.1 ラベルの参照
Maxima は入力と計算した結果を各々 %i と %o ラベルに保存 する. ここで,
% は %o の中で 最も数字の大きなもの を指す. そのため, % は Maxima
の処理が進むにつれて更新される.
入力ラベル %i と出力ラベル %o に割当てられた値を参照 する関数に, %, と
%th がある. % は 最新の結果を表示し, 最新の入力を返す. 又, %th は %th(6)
の様に用い, 6個前の結果を参照する.
更に, %i7 や %o8 とすれば, (%i7) 行で入力した式や, (%o8)
に表示された結果を参照することができる.
ただし, _ にはその様な使い方は出来ない.
入力と出力ラベルは kill(labels) で全て削除することができる. これ
を実行すると, 入力と出力ラベルに割当てられた値は消去されて, 各ラベルの
カウンタも 1 に戻される. そのため, 入力は再度 (%i1)
から開始することになる.
/home/inoue/bin/go tmp_lang/chunk-25.mx > tmp_lang/chunk-25.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-25.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-25.mx
1+2
3
resultant(x-t,y-t^2,t)
2
y - x
algsys([2*x+3*y = 1],[x,y])
2 %r1 - 1
[[x = %r1, y = - ---------]]
3
%
2 %r1 - 1
[[x = %r1, y = - ---------]]
3
_
%
%i1
batch(/var/www/html/LANG/tmp_lang/chunk-25.mx)
%o1
%o1
%i2
3
kill(labels)
done
/var/www/html/LANG/tmp_lang/chunk-25.mxこの例では, 様々な処理を行い, それらを % や で確認し, 最後に kill(labels) でラベル (%i や %o) の 内容を全て消 去する. ラベルの消去を行ったために, kill(labels) を入力した (%i10) から, (%o0) を経て (%i1) に初期化されてい ることに注目する.
23.2 結果の表示
Maxima では入力行に ; を付けると, Maxima が評価した値が表示され る. 数値の四則演算は実 行された後の値がデフォルトで表示される. ここで, 結果表示に関しては, Maxima は結果を2次元的に表示するのがデフォルトとなっ ている.
/home/inoue/bin/go tmp_lang/chunk-26.mx > tmp_lang/chunk-26.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-26.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-26.mx
2/5
2
-
5
integrate(f(x),x,a,b)
b
/
[
I f(x) dx
]
/
a
expand((x+1)*(x-1))
2
x - 1
/var/www/html/LANG/tmp_lang/chunk-26.mxこの表示は式が小さなものであれば良いが, 式が長くなると非常に判 り難いものになる. そこで, 表示を 1 行で済む様に指定が行える環境変 数 display2d がある. この変数の値が デフォルトの true であ れば, 2次元的な表示を行い, false を指定すると, 結果を1次元で表示する.
/home/inoue/bin/go tmp_lang/chunk-27.mx > tmp_lang/chunk-27.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-27.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-27.mx
display2d
true
'integrate(f(x),x)
/
[
I f(x) dx
]
/
expand((x+1)^3)
3 2
x + 3 x + 3 x + 1
display2d:false
false
'integrate(f(x),x)
'integrate(f(x),x)
expand((x+1)^3)
x^3+3*x^2+3*x+1
"/var/www/html/LANG/tmp_lang/chunk-27.mx"Maxima にはこの他にも特殊な表示を行う関数がある. 基本的に Maxima はキャラクター端末しかなかった昔のシステムでの利用を前提としていたため, 積分記号の様に文字を使って数式を表示する等の, ある意味では涙ぐましい努 力の跡がある. しかし, 近年の Window システムから見ると非常に古臭く感じ るものが多いのが現状である.
23.3 ラベルに関連する環境変数
● %
Maxima で処理されたもので, 最新の結果を指定する.
● %%
この値は Maxima-break の間に処理された最新の値である. 通常の入力では意
味を持たないが, 例えば, block 文の中で,(n-1) 行目の文の値を n 行目の文
で参照する場合には便利である.
例えば,
| 入力 | 表示 | 内部表現 |
|---|---|---|
| a-b; | a-b | a + (- 1) b |
| a/b; | \(\frac{a}{b}\) | \(a\,b^{-1}\) |
| sqrt(x); | sqrt(x) | \(x^{1/2}\) |
| x*4/3; | \(\frac{4\,x}{3}\) | \(\frac{4}{3}\,x\) |
は同値である.
● inchar:%i
Maxima の入力行ラベルで用いられる文字. 例えば, デフォルトでは i のため,
入力行ラベルは (%i1) の様に % の後に inchar で指定 した i
が続いている.
● outchar:%o
出力式の名前の先頭に付けられるアルファベットを指定する.
● linechar:%t
中間表示される際, 式の名前の前に置かれる文字を指定する.
● linenum
その時点での入力行番号が割当てられている.
● nolabels:false
true の場合, 入力値と計算結果をラベルに束縛しない. 即ち, %i や %o
等で入出力の参照が出来なくする. この様にすることで, batch
処理の空き領域を増すために kill(labels) を実行しなくて済む.
● prompt:
これは demo 関数のプロンプト記号を指定するもので, playback(slow) mode と
(Maxima-break) がある.
23.4 表示に関連する環境変数
● ibase:10
入力数値の基数.
● obase:10
表示の際に用いる数値の基数.
● absboxchar:!
絶対値を描く際に用いる文字を指定する. なお,
絶対値は精々一行の高さしかない.
● cursordisp:true
true であれば式が論理的列として描かれる. これはカーソルの移動が可能
なコンソールでのみ動作する. false であれば, 式は行から行へと単純に表
示される. cursordisp は writefile が有効であれば false になる.
● display2d:true
false であれば, 結果表示が2次元的な書式ではなく, 一行に収まる様に表示
される. 長い式や複雑な式, 表示に余裕が無い場合には特に便利である.
● display_format_internal:false
true が設定されていれば, 内部の数学的表現を隠した表示ではなく,
内部表現を反映した表示に 切り替わる. 従って,
内部表現そのもので表示するものではない. ここでの出 力は part
関数に対応するものではなく, inpart 関数に準じたものになると
も言える.
tcl_output([x1,y1,x2,y2,x3,y3],1) --> @{x1 x2 x3 @}
tcl_output([x1,y1,x2,y2,x3,y3],2) --> @{y1 y2 y3 @}
tcl_output([1,2,3,4,5,6],1,3) --> @{1 4@}
tcl_output([1,2,3,4,5,6],2,3) --> @{2 5@} ● %edispflag:false
自然底 %e の羃表示を定める環境変数である. デフォルトの false の場 合, %e
の負の羃は負の羃のまま羃表示される. 例えば, exp(-x) は %e の負の羃
%e^(-x) で表示される. true の場合, %e の負の羃は %e
の羃の商の形式で表示される. 即ち, %e^(-x) は 1/%e^x
の形式で表示される.
/home/inoue/bin/go tmp_lang/chunk-28.mx > tmp_lang/chunk-28.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-28.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-28.mx
exp(-x)
- x
%e
%edispflag:true
true
exp(-x)
1
---
x
%e
/var/www/html/LANG/tmp_lang/chunk-28.mx● exptdispflag:true
true であれば, Maxima は負の羃を持った項を分数式で表示する. 例えば,
x^(-1) は 1/x で表示される.
● lasttime
直前に入力した式の計算時間をミリ秒単位で time と gctime
の組合せを成分とするリストである.
● linel:79
一行に表示される文字数を設定する. いつでも変更できるが, 長過ぎたり,
短か過ぎたりすれば, 実用的ではない.
● pfeformat:false
true であれば, 有理数は行の中で表示され,
整数の分母は有理数の積として表示される. 例えば, 入力が b/4 であれば,
1/4*b と表示される. ただし, a/b の様に, a,b の両方が 不定元であれば,
通常の プリティプリントで表示される.
● showtime:false
true であれば, 出力式と共に計算時間の自動表示を行なう. showtime:all
とすれば, CPU 時間も含めて Maxima は計算処理に於け るメモリのゴミ収集
(gc) に費した時間も零でなければ表示する. この時間 は time=
の時間表示に含まれている. なお, time= には計算 時間のみが含まれ,
中間表示時間やファイルを読込む時間は含まれておらず, gc
への反応性に分けて認識することが難しいため, 表示される gctime には計算
の実行中に費やした全ての gctime を含んでいる. それ故, 稀に time= よりも
gctime の方が大きくなるかもしれない.
● stardisp:false
デフォルトの false の場合, 可換積演算子は出力では省略されている. true
であれば, 可換積演算子 * を表示する.
● ttyoff:false
true であれば入力行の表示のみを行い, 通常の出力を止める. ただし, エラー
表示は行なう. なお, writele を開いたファイルに対しても,
同じ出力となる.
23.5 エラー表示に関連する環境変数
● error_size:10
エラーメッセージの長さを制御する. error_size
よりも大きな式は文字列に置換され, 文字列には式が設定 されている.
文字列は利用者が設定可能なリストから取られる. この環境
変数のデフォルト値は利用者のが置換えてもかまわない.
● error_syms:[errexp1,errexp2,errexp3]
エラーメッセージで, error_size よりも大きな式は文字列に置換され,
その文字列には式が設定されている. 文字列は error_syms リスト
から取られて初期値は errexp1, errexp2, errexp3 となっている. エラー
メッセージが表示された後, 例えば, “the function foo doesn’t like errexp1
as input” であれば, errexp1; と利用者が入力すると, その
式を見ることができる. 必要であれば, error_syms に 別の文字列を
設定してもかまわない.
23.6 利用者の環境設定に関連する環境変数
● myoptions:[]
利用者が設定した全てのオプションを蓄えるリストである.
● optionset:false
true であれば, Maxima はオプションが再設定された時点でメッセージを表示
する. これはオプションの綴りが不確かな場合, 割当てた値が本当にオプ
ションの値となっているかを確認したいときに便利である.
23.7 デバッグに関連する環境変数
● debugmode:false
true の場合, エラーが生じたときや false
で中断モードに入ったときはいつでも Maxima の break loopに入る. all
が設定されていれば, 実行中の関数のリス トに対して backtrace
を調べることができる.
● ttyintfun:false
ttyinnum に設定された中断文字が入力された時点で, 動作する関数を制御す
る. この機能を利用するためには, ttyintfun(デフォルト値は false で, こ
の機能が使われていないことを意味する)
を引数を持たない関数として設定する. ここで, ttyinnum をデフォルトの 21
のままにしていれば, (Cntrl-u) が入力されたときに, この関数が動作する.
例えば, for 文のループで増分が i で for 文を動かしている間に i
の値を簡単に確認したければ次の様に行なる:
ttyinnum:21$ ttyintfun:printi$ printi():=print(i)$ すると, u を
打ち込めばいつでも変数 i の検査が行える様になる.
● ttyintnum:21(control+u(^u) のアスキーコード値に対応) これはどの文字が中断文字になるかを制御する. u は記憶を補助する変数 (mnemoric value) として選ばれている. 他の利用者は u を何か他のことで利用している訳でも 無い限り, ttyintnum を再設定すべきではない.
● values:[]
全ての値が束縛されたアトム, 即ち, 利用者変数で, Maxima のオプションや大
域変数では無いもので, :, ::
や関数等で値を束縛されたものを含むリストである.
/home/inoue/bin/go tmp_lang/chunk-29.mx > tmp_lang/chunk-29.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-29.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-29.mx
values
[]
a:1
1
values
[a]
/var/www/html/LANG/tmp_lang/chunk-29.mx23.8 ラベル処理に関連する関数
● %th(n)
“正整数” n 番前の計算結果を取り出す. この %th は batch ファイル
では非常に便利である. これは %o ラベルの値が batch ファイルをどの
時点で処理するかで異なるのに対し, %th はその関数を実行する時点
を中心として, 結果が指定出来るからである.
● labels(char)
文字 %i, %o に %t を引数として取り, 全ての %i-ラベル, %o-ラベル や
%t-ラベル のリストを各々生成する, もし, solve で沢山の %o-ラベル
を生成した場合は firrst(rest(labels(%o))) とすれば, 最新 の
%o-ラベルが何で あるかが判る.
labels は引数として任意の記号名を取り, inchar, outchar や linechar を再
設定すれば, ラベルのリストを返すが, ラベルの最初の文字は labels に
与えた引数の最初の文字に適合する. 変数の labels はデフォルト値が無設
定の c, d と e 行の値が設定されたもののリストとなる.
23.9 式の表示に関連する関数
● disp(exp_1, exp_2,…)
display に似ているが, 引数の値のみを表示する.
● dispcon(tensor_1,tensor_2,…)
● dispcon(all)
defcon に対して与えられた \(\rm
tensor_i\) の縮約属性を表示する. dispcon(all)
は定義されている全ての縮約属性を表示する.
● display(exp_1, … , exp_n)
式exp_1, … , exp_n を表示する. その左側が未評価の式で, その右側の行の
中心がその式の値となる. この関数は block や for 文で, 途中結果の表示を
行うのに便利である. display の引数は通常, アトム, 添字された変数や関数の
呼出しである.
● dispterms(exp)
引数の成分を一つづづ, 一つの成分を表示すると下に次の成分を表示して行く.
つまり, 最初に 式 の演算子が表示され, 和の各項, 積の因子, より一般の式
の成分が分離されて表示される. これは, 式が表示にとても大きいときには便
利である. 例えば, p_1, p_2, … がとても大きな式ならば, 表示プログラムは
p_1+p_2+… を一度に表示しようとして, 保存領域を使い果してしまう
かもしれない. しかし, dispterms(p_1+p_2+…) は p_1 を最初に表示 すれば,
その下に p_2 を表示等々となる. dispterms を利用しないとき, もし,
指数式が a^b の形式で表示するにはとても長い場合, expt(a,b) (又は,a^(-b)
の場合は ncexpt(a,b)) で表示される.
● expt(a,b)
指数式が a^b で表示されるのに余りにも大き過ぎる場合は expt(a,b), a^(-b)
の場合は ncexpt(a,b) と表示する.
● grind(arg)
引数 arg を string 関数よりも, より読み易い書式で表示する. 値として
%o-行を返す.
● ldisp(exp_1, exp_2, … )
disp に似ているが, 中間ラベルを生成する点で異なる.
/home/inoue/bin/go tmp_lang/chunk-30.mx > tmp_lang/chunk-30.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-30.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-30.mx
ldisp(x^2+y)
2
(%t2) y + x
[%t2]
/var/www/html/LANG/tmp_lang/chunk-30.mx● ldisplay(exp_1, exp_2, … )
display に似ているが, 中間ラベルを生成する点が異なる.
● nostring(arg)
後戻しを行っているときに, 全ての入力行を string で文字列にする代りに,
その表示を行なう. 引数 が grind であれば,
その表示はより読み易い書式となる. なお, playback([5,10],20,time,slow)
の様に, 任意の数のオプションを入れてもかまわない.
● print(exp_1, exp_2, …)
式exp_1がら順番に評価を行い, その結果を表示する. ここで,
式exp_iに含まれる アトムや関数の前に単引用符’ が置かれていたり, 文字列
(全体を二重引用 符で括ったもの) の場合は, 評価を行わずに,
そのままで表示を行なう.
● tcl_output(List, index, step)
● tcl_output(list, index)
添字 index を展開したリスト List に対応 する tcl のリストを表示する.
ここで, 飛幅 step の初期値は 2 で,
引数がリストで構成されたリストではなく, 数値リスト 形式の場合,
飛幅から外れた全ての要素が表示される.
- argi=labels であれば, 古くなった全ての入力, 中間行, 出力行 (他
の名付けられていない項目を除く) が消去される.
- argi=clabels であれば, 入力行だけが消去される.
- argi=elabels であれば, 中間の t-行のみが消去される.
- argi=dlabels であれば, 出力行のみが消去される.
- argi が任意の他の情報のリスト (要素は Maxima 変数の infolists
のもの) の名前であれば, そのクラス (とその属性)
の全ての項目が削除される.
- argi=all であれば, 以前定義された全ての情報リストに関する全ての
項目が labels と同様に削除される.
- argi=数値 (n とする) であれば, 最後の n 行 (つまり, 最後の n 個
の行) が消去される.
- argi が [m,n] の形式であれば, m と n の間に含まれる行番号の行が 全て削除される.
● reveal(exp, depth)
深度 depth は整数値で指定された各々の成分の長さで 式 exp を表示する.
和は sum(n), 積は product(n) として表示される. ここで n は
和や積の成分の数になる. 指数関数は expt で表現される.
/home/inoue/bin/go tmp_lang/chunk-31.mx > tmp_lang/chunk-31.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-31.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-31.mx
aa:integrate(1/(x^3+2),x)
aa
1/3
2 x - 2
atan(------------)
2 1/3 2/3 1/3 1/3
log(x - 2 x + 2 ) 2 sqrt(3) log(x + 2 )
(- -----------------------) + ------------------ + -------------
5/3 2/3 2/3
3 2 2 sqrt(3) 3 2
reveal(aa,1)
Sum(3)
reveal(aa,2)
Negterm + Quotient + Quotient
reveal(aa,3)
atan log
(- Quotient) + ---------- + ----------
Product(2) Product(2)
reveal(aa,4)
log atan(Quotient) log(Sum(2))
(- ----------) + -------------- + -----------
Product(2) Expt sqrt 3 Expt
reveal(aa,5)
Sum(2)
atan(----------)
log(Sum(3)) Product(2) log(x + Expt)
(- -----------) + ---------------- + -------------
3 Expt 2/3 2/3
2 sqrt(3) 3 2
/var/www/html/LANG/tmp_lang/chunk-31.mx● show(exp)
式 exp を添字された対象として表示する. その際, 共変添字を下添字, 反変添
字を上添字として表示する. 微分添字は下添字として表示され, コンマで共
変添字が分離されている.
● tex(exp)
● tex(exp, fname)
● tex(label, fname)
与えられた式 exp や ラベル行 label を TEX の書式に変換する. ファイル名
fname を指定 すると, 出力結果は指定ファイルに保存される. なお,
指定ファイルが既存 の場合, 結果はそのファイルの末尾に追加される. なお,
ラベル行を変換する 場合, 式のラベル番号も生成される.
/home/inoue/bin/go tmp_lang/chunk-32.mx > tmp_lang/chunk-32.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-32.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-32.mx
d1:integrate(1/(1+x^3),x)
2 x - 1
2 atan(-------)
log(x - x + 1) sqrt(3) log(x + 1)
(- ---------------) + ------------- + ----------
6 sqrt(3) 3
tex(d1)
$$-{{\log \left(x^2-x+1\right)}\over{6}}+{{\arctan \left({{2\,x-1
}\over{\sqrt{3}}}\right)}\over{\sqrt{3}}}+{{\log \left(x+1\right)
}\over{3}}$$
false
tex(integrate(sin(x),x))
$$-\cos x$$
false
tex(d1,"/tmp/out.tex")
false
/var/www/html/LANG/tmp_lang/chunk-32.mx● box(exp)
● box(exp, label)
式 exp を文字で囲んで返す. この箱は式の一部でもある. なお, box(exp,
label) とすると 式 exp を文字で囲み, 上に ラベル label を表示する.
ただし, ラベル が長ければ, 表示の際に切捨てられてしまう. なお, 環境変数
boxchar に box, dpart や lpart 関数で与えられた文字列を囲む際
に使う文字を割当てる.
/home/inoue/bin/go tmp_lang/chunk-33.mx > tmp_lang/chunk-33.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-33.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-33.mx
box(" this is a pen. ")
""""""""""""""""""
" this is a pen. "
""""""""""""""""""
box(" this is a pen. ","maxima")
"maxima"""""""""""
" this is a pen. "
""""""""""""""""""
boxchar:x
x
box(" this is a pen. ","maxima")
Maxima encountered a Lisp error:
Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-TYPE-ERROR: $X is not of type SEQUENCE:
Automatically continuing.
To enable the Lisp debugger set *debugger-hook* to nil.
/var/www/html/LANG/tmp_lang/chunk-33.mx● dpart(exp, n_1, … , n_k)
式 exp の内部表現から, n_1, … , n_k で指定される部分式を文字で囲んで
式全体を表示する. この囲まれる部分式 は part
関数で抜出す部分式になる.
/home/inoue/bin/go tmp_lang/chunk-34.mx > tmp_lang/chunk-34.out 2>&1
batch("/var/www/html/LANG/tmp_lang/chunk-34.mx")
read and interpret /var/www/html/LANG/tmp_lang/chunk-34.mx
dpart(x+y/z^2,1,2,1)
y
---- + x
2
"""
"z"
"""
/var/www/html/LANG/tmp_lang/chunk-34.mx● lpart(label, exp, n_1, … , n_k)
dpart に似ているが, ラベル付けられた箱を用いる. ラベル付けられた箱 は
dpart で生成したものに似ているが, 上の行に名前がある点で異なる.
● rembox(exp, arg)
式 exp から 引数 argに沿って box を削除する. 引数 が unlabeled,
全てのラベ ル付けされていない box が削除される. 引数
があるラベルの名前であれば, そのラベルを伴う box だけが削除される. 引数
が省略されると, 全ての box が削除されてしまう.
23.10 システムに関連する関数
● alias(new_name_1, old_name_1, … , new_name_n, old_name_n)
(利用者, 又はシステム) 関数, 変数, 配列等に別名を与える. 引数は新名
称と旧名称の一組となるので, 偶数個の引数が必要になる.
● debug, debugprintmode, LISPdebugmode
これらの関数は引数を必要としない. debug() の様に使う, LISPdebugmode();
debugprintmode(); と debug(); は
システムプログラマーが使う虫取り機能を利用者が使える様にする. これ
らのツールは強力であるが, 幾つかの取決めが通常の Maxima
のものと異っている. これらの命令は Maxima
言語で構築した関数が上手く動作する様に虫取
りしなければならない利用者向けに設計されている.
● kill(arg_1, arg_2, …)
Maxima から指定した引数を消去する. 第 i 引数 arg_i が変数
(単配列要素を含む), 関数, 又は配列の場合, 指定された項目は,
その属性の全てと一緒に Maxima の中核から消去される.
to_lisp();
type (to-maxima) to restart, ($quit) to quit Maxima.
Maxima> (setq $a '1)
1
Maxima> (to-maxima)
returning to Maxima
(%o1) true
(%i2) a;
(%o2) 1 kill(values) や kill(variabkes) で同じ式を指定するラベル
が消去される迄, メモリの占有領域を解放しないことに注意する. 例えば,
大きな式が %i7 行の x に対して割り当てられていた場合, 占有され
た保存領域を解放するためには, kill(x) と kill(%o7) も実行し
なければならない.
kill(allbut(name1,…,namek) は kill(all) を, その名前を allbut
で指定したものを 除外して実行する (注意: namei は, u, v, f, g
の様な名前を意味し, functions の様な infolist ではない). kill は
与えられた引数から全ての属性を削除するので, kill(values) は values
リストの全ての項目に関連する全ての属性を削除するが, それに対して remove
関数群 (remvalue, remfunction, remarray, remrule) は指定し
た属性を削除する. 更に, 後者はリストの名前か指定した引数が存在しなけ
れば false を返すが, kill は指定した項目がたとえ存在しなくても 常に done
を返す. 式の削除は, あまりにも多くの fasl ファイルが読 み込まれたり,
メモリの割当ての水準が高くなり過ぎたかの何れかの理由によ り, no core
-fasload という文句が出る問題への対処にはならない. 式の削
除は単に幾つかの領域を空にするだけで, より小さくすることではない.
● remfunction(func_1, func_2, … )
利用者の定義関数を Maxima から削除する. 利用者定義の関数は環境変数
functions にその名 前が保存されており, remfunction はこの functions に
含まれている関数の削除を行なう. なお, all が 唯一の引数であれば
functions に含まれる全ての利用者定義の関数が削除される.
● reset()
全ての Maxima の初期化を行なう. この場合, 全ての環境変数の値の殆どが
デフォルト値に戻されるが, 一部, linel の様に割当によってのみ変更可能
な表示に関連する環境変数は Maxima の 計算機能として考えられているため,
この初期化はされない.
● sstatus(feature, package)
状態を設定することを意味する. status(feature, hack_package) が true
を返す様に
sstatus(feature, hack_package) を用いることができる.
これはパッケージを書く場合, それらが読み込まれた
機能の記録を保つのに便利である. sstatus(feature, hack_package)
はその名の通り, 状態を設定することを意味する.
● playback(arg)
入力と出力行の後戻し (play-back) を実行する. arg=n(整数) であれば,
最近の n 個の式 (ci, di と ei を各々1 で数える) が後戻しされ, arg が省
略されていれば, 全ての行となる. arg=input であれば, 入力行が後戻し され,
arg=[m,n] であれば, m から n 迄の間に含まれる全ての行が後 戻しされる.
もし, m=n であれば, [m] だけで引数としては 十分である. arg=slow
であれば, デモ(その対極としては”速い” batch) の様に遅く後戻しを実行する.
これは有用な式を取り出す目的で, save や stringout
と連携して第二の保存ファイルを生成するときに便利である. もし, arg=time
であれば, 計算時間が式と同様に表示される. もし, arg=gctime か totaltime
であれば, showtime:all;
を用いたのと同じ様に計算時間の完全な詳細が表示される. arg=string
であれば, 全ての入力行を文字列として返し (string 函数を参照),
それらを表示すると云うよりは後戻しをする. arg=grind であれば, “grind”
モードに (入力行の進行に対して) 切り替わる (grind を参照).
playback([5,10],20,time,slow)
の中のオプションの様に任意の数を含んで良い.
● system(command)
オペレーティングシステムの命令等の Maxima 外部の命令を実行する. オプ
ションを持つ命令 を実行したければ, 命令全体を文字列として system 関数
に引渡する. 例えば, ls -a を実行したければ, system(“ls -a”);
と入力する.
● quit()
Maxima を停止させる. 入力は引数無しで quit(); 或いは quit()$ と入力する.
単に quit だけでは意味がない. なお, Maxima
を一時的に停止させるのであれば, Cntrl-C(^C) を入力する.
● to_lisp
● collapse(exp)
全ての共通 (つまり, 等しい) 部分式を共有する (つまり, 同じセルを用いる)
ことで引数を消去し, 領域を節約する (collapse は optimize
命令で用いられる サブルーチンである). それ故, fassave を使う前や save
で保存したファイ ルを読み込んだ後に collapse
を呼出すことは便利である.
collapse([expr1,…,exprn]) を用いて, 幾つかの式を一緒に潰すこと
も可能である. 同様に, collapse(listarray(’a)) とすることで,
配列の成分を消去することも出来る.
● ?
関数や変数の前置詞として, 関数や変数が LISP の表記であって, Maxima の表
記では無いことを識別する. 二つの疑問符 ?? は Maxima の現行の Maxima の命
令行の内容を空にする.
24 LISP に関連する関数
24.1 Maxima と LISP
Maxima は Common LISP と呼ばれる LISP の一方言で記述されている. LISP
は関数型と呼ばれるプログラム言語で, 様々な関数を定義し,
それらを組合せてプログラムを記述する. なお, C や FORTRAN は手続型と呼ば
れる. Maxima はこの LISP の上で動作する環境であるが, Maxima 自体は
PASCAL 風の言語仕様を持っており, 構文的にも LISP を意識することは単純な
利用では殆どない.
ただし, Maxima で処理エラーが発生したときに LISP
のデバッガに落ちることがある. LISP のデバッガからの抜け方は, Maxima
を実装した LISP によって微妙に異 なるが, CLISP の場合は :q と入力すると
Maxima に戻る.
LISP の特徴は言語仕様が非常に柔軟な点である. LISP にはアトムと呼ばれる変
数があり, それらを空白で区切って小括弧 () で括ったリストと呼ばれるデー
タが, 最も基本的なデータとなる. このリストはリストのリストといっ
たものも許容する. このアトムとリスト等で構成されたデータ を S 式と呼ぶ.
なお, LISP のプログラム自体も S 式である. そのため, LISP の関数でプ
ログラムを操作することも容易に行える.
そのため, Maxima のプログラムでは足りない所を LISP
で代用することも多くある. 又, Maxima から LISP
を直接利用することもできる. この場合は Maxima の to_LISP 関数を利用する.
Maxima で to_lisp(); と入力 すると, 裏方の LISP が表に出る. これで LISP
を使って遊べる. この 状態から Maxima に戻りたければ, (to-maxima)
と入力する. すると通常の Maxima に戻る.
(%i1) a:x+y+z;
(%o1) z+y+x
(%i2) :lisp $a;
((MPLUS SIMP) $X $Y $Z)
(%i2) :lisp (car $a)
(MPLUS SIMP)
(%i3) ?car(a);
(%o3) ("+", simp) この例では to_lisp(); で LISP に入って, アトム $a に 1
を割当てている. その後 (to-maxima) で Maxima に戻っている. to_lisp()
関数の返却値は true である. 最後に a; を入力すると, LISP で $a
に割当てた値 1 が返却される. これは Maxima でのアトムの内部表現では $a
の様に先頭に $ が付くためである. この例で注目して頂きたいことは, Maxima
で表示されているものと LISP 側で見たものと様子が違うことである. 即ち,
Maxima で扱うデータ, 更には関数 それ自体も LISP
側では別の表記方法がある. この LISP 側での表現を単
純に内部表現と呼んでいる. この内部表現を通常の処理で気にすることは殆ど
ないが, 細かな処理を行う必要がある時点で初めて意識することになる.
なお, Maxima の関数名で先頭に ? が付いているものが幾つか存在する. この様
な関数は ? を外した部分は LISP の関数で, Maxima から裏の LISP
で処理させて, その結果を Maxima 側に返す関数である.
? は通常の LISP の関数にも適応可能で ? を頭に付けた関数は, Maxima 内
部では ? を外して, LISP の関数として処理される. この様に Maxima
が介在するため, ? を用いて LISP の関数を利用する場合には, 引数は Maxima
で見えているものを設定する. なお, ? と関数の間に 空白を入れると Maxima
のオンラインマニュアルを呼出そうとするので, 注意が必要である.
? と似た関数に :lisp がある. こちらは, 直接 LISP の S 式を Maxima
側から入力し, LISP に評価させた値を得るための関数である. ? との違いは, ?
では引数が LISP の関数で, その引数は Maxima に準じたものとなるが, :lisp
の場合はより一般的な
LISP の S 式となる. そのため, 引数も Maxima
の内部表現そのものとなる.
(%i37) ? inte;
0: (maxima.info)Introduction to Elliptic Functions and Integrals.
1: Definitions for Elliptic Integrals.
2: Integration.
3: Introduction to Integration.
4: Definitions for Integration.
5: INTERRUPTS.
6: ASKINTEGER :Definitions for Simplification.
7: DISPLAY_FORMAT_INTERNAL :Definitions for Input and Output.
8: INTEGERP :Definitions for Miscellaneous Options.
9: INTEGRATE :Definitions for Integration.
10: INTEGRATE_USE_ROOTSOF :Definitions for Integration.
11: INTEGRATION_CONSTANT_COUNTER :Definitions for Integration.
12: INTERPOLATE :Definitions for Numerical.
Enter space-separated numbers, ALL or NONE: 上記の例では変数 a に x+y+z を割当ているが, $a が変数 a の内部変数名となる. :lisp $a; で この変数に割当てた値を参照するが, 返却値は内部表現そのものである. この様な変数の参照は ? では出来ない. 更に, :lisp (car $a); の値は内部表現そのものが返される.一方, ?car(a); の値はそれを Maxima で解釈した (“+”, simp) となっていること, 引数に $ が付いていないこと, および ;lisp の結果に %o ラベルが 無いことに注目する. この様に, ? は入力と出力に Maxima が介在するために, 入出力をする度に Maxima の評価を受けることになるが, :lisp の 場合は直接操作となる. :lisp は Maxima で内部表現を確認する 必要がある場合に特に便利な関数である. なお, Maxima は LISP で記述されてい るため, そのデータだけではなく, 全てが LISP の S 式で, LISP の関数で処理 が可能となる. このことを利用して Maxima の機能を拡張することが容易に行 える. 各種データの内部表現については各々の章で必要があれば解説を行なう.
24.2 LISP に関連する関数
● ?LISPの関数
演算子 ? を LISP の関数の頭に付けることで, Maxima から LISP
の関数が利用可能となる. 関数の記述方法は Maxima 風に行い, 引数も Maxima
側で見えている変数名 (内部表現では通常アトムの先頭に $ が付いている)
を与える. 又, 返却値も Maxima の解釈を経たものとなり,
内部表現そのものが返却される訳ではない. なお, ? と LISP の
関数の間には空白を入れてはならない. 空白を入れた場合, Maxima は
describe(引数) と解釈して, 引数に関連したオンラインマニュアルを
起動しようとする. そのため, オンラインマニュアルが起動してしまうか,
或いは結果として false が返却されることになる.
● :lisp S式
:lisp の後に空白を入れて LISP の S 式を続けると, LISP 側で S 式
を評価し, その結果を Maxima に返す. なお, 結果は %o ラベルに
は蓄えられず, 内部表現がそのまま返される.
● to_lisp(), (to-maxima) と (continue)
to_lisp() は Maxima から LISP に移行するための関数で, 引数は必要 ない.
to_lisp で制御は Maxima から LISP に移される. こ の時点でプロンプトが
Maxima> に変化する. LISP から Maxima に 戻る関数は (to-maxima)
である. この関数も引数は不要である. この函 数を実行すると, Maxima は
to_lisp() を入力した入力行の結果とし て true を返し,
セッションを再開する. 又, (continue) も LISP から Maxima 戻る際に使える.
動作は (to-maxima) と同様である.
23.3 ヘルプについて
Maxima にはオンラインヘルプがある. オンラインヘルプを参照するために は, DESCRIBE か ? を用いる. 使い方は, describe(“inte”), 或いは, ? inte とすると inte を含む事項が以下の様に表示される.
(%i1) :lisp (foo 1 2) 後は番号を入力するか, all を入力する. 他に, 関数のデモを実行する DEMO 命令と例題を実行する EXAMPLE 命令がある. どちらも各命令の実行 後に中断し, スペースキーを押すと次の例題を実行する. なお, デモファイル の拡張子は .dem である.
24.4 LISP と Maxima
Maxima の全ては lisp で記述されている. そのため, 関数と変数の名前の変 換がある. lisp の 階層で $ で始まる全ての記号は Macsyma の階層では $ を外して読まれる. 例えば, 二つの lisp の関数 TRANSLATE と $TRANSLATE がある. Maxima の階層で TRANSLATE(FOO); と入力すると, 内部 で呼出される関数は $translate 関数になる. もう一方の関数を 呼出すためには, ? を前に置く. なお, ? の後には空白を入 れてはいけない. LISP 命令を直接入力したければ, :lisp 命令を使って,
(%i1) Integrate;
(%o1) INTEGRATE
(%i2) Integ;
(%o2) Integ の様にするか, to_lisp(); を使って直接 LISP を表に出す方法, debug
break に入るために Ctrl-c を使う方法を用いる. それか ら, $%o2
の評価を行えば, ラベル %o2 行の値を内部 LISP の 書式で見られる. 更に, :q
と入力するとトップレベルに戻る. もし, to lisp(); で Maxima
を抜けていれば, LISP プロンプトに続け て (run) か (to-maxima)
と入力する.
Macsyma の階層で呼出せる LISP の関数を書きたければ, それらの名前は $
で始まる様にしなければならない. LISP の階層で入力された全て の記号は
|$odeSolve| の様にでもしない限り, 大文字で自動的に読込 まれる. もし,
記号が既に読込まれていた場合や, 最初の読込んだ時点で,
大文字だけの同名の記号がまだ存在しなければ, Maxima はその記号を大文字
と小文字が混在したものとして解釈する.
(setq $foo #$[x,y]$) 記号 Integrate は Maxima の予約語(プリミティブ)のために,
その大文字が既に存在し ている. しかし, Integ はまだ存在していないので,
Integ は Maxima に受け入れられる,
これは幾らか曖昧に見えるかもしれないが, Maxima
のプリミティブが大文字であろうが小文字であろうが, 古い Maxima
のプログラムの動作保証(サポート)のために設定されている.
このシステムの長所は, LISP の 階層で入力しても, 即座に Maxima
のキーワードであるか,関数であるかを判 別できることである.
LISP の階層で Maxima の書式を入力をするためには, #$
マクロを用いてもよい.
(%i1)FOO:[X,Y]; (displa $foo) 例外は VALUES リストに foo が現れないことである. Macsyma の表示書式で foo を見るためには次の様に入力しなければならない:
(%o2) FOO(X, Y) := X + Y + 3 この文書では, Maxima の記号を参照するときに, Maxima
の階層で入力するの と全く同様に$ を 省略する. これは, LISP
の記号を参照するときには 混乱の原因となる. この場合, 通常の LISP
記号に対しては小文字を用い, Macsyma の記号に対しては大文字を用いる.
例えば, $list には LIST, 表示名が “list” の LISP の記号には list とする.
Maxima 言語で定義された関数は通常の LISP 関数ではないので, それらを呼
出すために mfuncall 関数を使わなければならない.
例えば:
MAXIMA> (mfuncall '$foo 4 5)
12
MAXIMA> (macsyma:typep '(1 2)) ==> 'list
(lisp:typep '(1 2))==> error (lisp:type-of '(1 2))==> 'cons となる. 幾つかの LISP 関数が Maxima パッケージに潜んでいる. 何故 なら, それらを Maxima で利用しても, システム関数の定義と互換性が無いか らである. 例えば, typep は MacLisp と Common LISP での挙動は異なる. もし, Maxima のパッケージで zeta lisp の typep を参照したければ, global:typep(又 は Common Lisp では cl:typep) を用いなけ ればならない. つまり,
/*-*-Maxima-*-*/
setup_autoload("vect");
showtime:all;
testdata:"nekoneko"; となる.
どの記号が裏に潜んでいるかを参照するためには,”src/maxima-package.lisp”
を参照するか, LISP 階層でパッケージの describe 関数を実行する.
24.5 ごみ集め
記号処理は膨大なゴミの生成を行う傾向があり, この効率的な実装は, ある種 のプログラムの完遂にとって非常に重要なことになる. mprotext システム コールが利用可能な UNIX システム (SunOS 4.0 や BSD の幾つかを含む) 上 での GCL では多重層のゴミ集め機能が利用できる. これは最近書き込まれ たページの回収に限定される. ALLOCATE や GBC に関する GCL の文書を参 照する. LISP 階層で (setq si::notify-gbc t) を実行すれ ば, どの領域がより多くの空領域が必要とするのかを決定する手助けになる.
25 Maxima の実行環境について
25.1 Maxima の初期化
Maxima を起動する際に, Maxima をカスタマイズするためのファイル maxima-init.mac が自動的に 読み込まる. なお, このファイルは Maxima を起動するディレクトリ上に置く必要がある. maxima-init.mac には Maxima の関数や環境変数の設定が記述できる. 特に, setup_autoload 関数を用いると, 必要な パッケージの読込が自動的に行える. 以下に簡単な例を示す.
/*-*-Maxima-*-*/
setup_autoload("vect");
showtime:all;
testdata:"nekoneko";先ず, 註釈は /* / で囲む. この例では頭に, /--Maxima--*/ と置いて Maxima 言語のファイルで あることを示しているが, わざわざ書込む必要性はない. 次の setup_autoload は初期化ファイルの中で関数を 自動的に読込む際に用いる. その後には環境変数 showtime の設定による Maxima の環境設定を行なっている. この初期化ファイルには利用者独自の物を書込める. この例ではアトム testdata に文字列 “nekoneko” を 割り当てている.
25.2 中断の方法
Maxima の計算を中断したければ, 通常は制御文字 c(Cntrl-c) を用いる. Maxima は z(Cntrl-z) が入力されて も中断するが, この場合は Maxima を出て UNIX の shell レベルに戻るの で, 通常は Cntrl-c で計算を中断して break loop に入る. なお, :t と入力すれば Maxima の最上層に再び戻る.
25.3 関数
● room()
● room(true)
● room(false)
保存領域の状況を詳細な記述で出力して Maxima の管理に蓄える. これは lisp
の room 関数を利用している. room(false) - 非常に詳細な記述を出力するか,
大半は同様の情報を含んでいる.
● setup_autoload(fname, func_1, … , func_n)
ファイル, 関数名, “funci” で, “funci” の呼出しを行い, “funci”
が定義されていなければ, “file” によるファイルの指定は自動的に load に
よって読み込まれなければならず, その file には “funci” の定義を含んで
いなければならないことを指示する (これは呼出しによる過程, 例えば, Maxima
で integrate が様々なファイルを読み込む原因となる). Maxima でファイル
を扱う他の命令での様に setup_autoload の引数は評価されない.
setup_autoload は配列関数に対しては動作しない.
● status(arg)
Maxima に関する様々な情報を与えられた引数に従って返却する.
使える引数と結果を以下に示す:
- time 計算で消費した時間.
- day その週の日
- date 年, 月, 日々のリスト
- daytime 時間, 分, 秒のリスト
- runtime 現時点の Maxima で集計された cpu 時間に原子”milliseconds”をかけたもの.
- realtime 利用者が Maxima を立ち上げてから経過した実際の時間 (秒単位).
- gctime 計算で費やしたゴミ集め (garbage collection) 時間
- totalgctime Maxima でゴミ集めに費やした総時間.
- freecore アドレス空間を使い果す前に拡張可能な Maxima
のコアブロックの 数 (1ブロックは 1024 語). 250*blocks(mc
にて得られる最大値) か ら値を減じ, Maxima
が使い上げた中心核のブロック数を知せる (固定ファ イル無しの Maxima
は大体 191 ブロックで開始する).
- feature システム機能のリストを返す.
● time(%o1, %o2, …)
%oi の計算で費した計算時間をミリ秒単位で表記したリストを返す. (注:変数
showtime:false を true にすると, 各%o-行 (結果表示行)
で計算時間が表示される).
(%i17) showtime;
(%o17) false
(%i18) integrate(sin(x)*exp(-x),x,0,inf);
1
(%o18) -
2
(%i19) showtime:true;
Evaluation took 0.00 seconds (0.00 elapsed) using 72 bytes.
(%o19) true
(%i20) integrate(sin(x)*exp(-x),x,0,inf);
Evaluation took 0.02 seconds (0.02 elapsed) using 109.234 KB.
1
(%o20) -
2
(%i21) time(%o18,%o20);
Time:Evaluation took 0.00 seconds (0.00 elapsed) using 96 bytes.
(%o21) [0.015998, 0.015998]
付録 Mathematica
Mathematica から Maxima へ
| Mathematica | Maxima |
|---|---|
| ◆ 定数 | |
| Pi | %pi |
| E | %e |
| I | %i |
| Infinity | inf minf |
| ◆ 演算と数値 | |
| a+b | a+b; |
| a-b | a-b; |
| a*b | a*b; |
| a/b | a/b; |
| a^b | a^b; |
| Sqrt[a] | sqrt(a); |
| N[a] | float(a); |
| N[a,b] | fpprec:n; bfloat(a); |
| ◆ 方程式を解く | |
| Solve[f[x]==g[x],x] | solve(f(x)=g(x),x); |
| Solve[{f==g,h==k},{x,y}] | solve([f=g,h=k],[x,y]); |
| NSolve[f==g,x] | expand(float(solve(f=g,x))); |
| FindRoot[f(x)==g(x),{x,a}] | load(newton); newton(f(x)-g(x),x,a); |
| ◆ 多項式の操作 | |
| Expand[f[x]] | expand(f(x)); |
| Factor[f[x]] | factor(f(x)); |
| Together[f[x]] | ratsimp(f(x)); |
| Apart[f[x]] | partfrac(f(x)); |
| Cancel[f[x]] | ratsimp(f(x)); |
| ◆ 式の簡約化 | |
| Simplity[f[x]] | ratsimp(f(x)); |
| FullSimplify[f[x]] | fullratsimp(f(x)); |
| ◆ 複素数 | |
| a+b*I | a+b*%i; |
| Re[z] | realpart(z); |
| Im[z] | imagpart(z); |
| Abs[z] | cabs(z); |
| Arg[z] | carg(z); |
| Conjugate[z] | realpart(z)-imagpart(z)*%i; |
| ◆ リストや行列の作成 | |
| {a,b,c} | [a,b,c]; |
| {{a,b},{c,d}} | リスト:[[a,b],[c,d]]; 行列:matrix([a,b],[c,d]); |
| Table[a[i],{i,p,q}] | makelist(a(i),i,p,q); |
| Table[a[i],{i,p,q,r}] | makelist(a(p+(q-p)*r),i,1,(q-p)/r); |
| ◆ 行列の演算 | |
| a.b | a.b; |
| Cross[a,b] | transpose(adjoint(matrix(a,b,[1,1,1])))[3]; |
| Outer[f,a,b] | outermap(f,a,b); |
| Tr[a] | load(nchrpl); mattrace(a); |
| Det[a] | determinant(a); |
| Inverse[a] | invert(a); |
| Transpose[a] | transpose(a); |
| Eigenvalues[a] | load(eigen); eigenvalues(a); |
| Eigenvectors[a] | load(eigen); eigenvectors(a); |
| ◆ 三角関数 | |
| Sin[x] | sin(x); |
| Cos[x] | cos(x); |
| Tan[x] | tan(x); |
| ArcSin[x] | asin(x); |
| ArcCos[x] | acos(x); |
| ArcTan[x] | atan(x); |
| TrigExpand[f[x]] | trigexpand(f(x)); |
| TrigReduce[f[x]] | trigreduce(f(x)); |
| ◆ 指数と対数 | |
| Log[x] | log(x); |
| Log[10,x] | log(x)/log(10); |
| Exp[x] | exp(x); |
| ◆ 双曲線関数 | |
| Sinh[x] | sinh(x); |
| Cosh[x] | cosh(x); |
| Tanh[x] | tanh(x); |
| ArcSinh[x] | asinh(x); |
| ArcCosh[x] | acosh(x); |
| ArcTanh[x] | atanh(x); |
| ◆ 通常の演算 | |
| D[f[x],x] | diff(f(x),x); |
| Integrate[f[x],x] | integrate(f(x),x); |
| Integrate[f[x],{x,a,b}] | integrate(f(x),x,a,b); |
| Sum[x[k],{k,a,b}] | sum(x(k),k,a,b); |
| Product[x[k],{k,a,b}] | product(x(k),k,a,b); |
| Limit[f[x],x->a] | limit(f(x),x,a); |
| Series[f[x],{x,a,n}] | taylor(f(x),x,a,n); |
| ◆ 微分方程式 | |
| DSolve[f[y[x]]==0,y[x],x] | desolve(f(y(x))=0,y(x)); |
| または ode2(f(y(x))=0,y(x),x); | |
| DSolve[{f==0,g==0},y[x],x] | desolve([f=0,g=0],y(x)); |
| DSolve[{f==0,y[0]==a},y[x],x] | |
| atvalue(y(x),x=0,a); desolve(f=0,y(x)); | |
| ◆ 変換 | |
| LaplaceTransform[f[t],t,s] | laplace(f(t),t,s); |
| InverseLaplaceTransform[g[s],s,t] | ilt(g(s),s,t); |
| FourierTransform[f[t],t,w] | load(fft); fft(f(t),t,w); |
| InverseFourierTransform[g[w],w,t] | load(fft); ift(f(t),t,w); |
| ◆ 整数関数 | |
| Round[x] | ?round(x); |
| Mod[n,p] | mod(n,p); |
| GCD[a,b] | gcd(a,b); |
| LCM[a,b] | lcm(a,b); |
| FactorInteger[n] | factor(n); |
| Rationalize[x] | ratsimp(x); |
| ◆ 特殊関数 | |
| n! | n!; |
| BesselI[v,z] | bessel i(v,z); |
| BesselJ[v,z] | bessel j(v,z); |
| BesselK[v,z] | bessel k(v,z); |
| BesselY[v,z] | bessel y(v,z); |
| Erf[x] | erf(x); |
| Gamma[x] | gamma(x); |
| Zeta[x] | zeta(x); |
| ◆ グラフィックス | |
| Plot[y,{x,a,b}] | plot2d(y,[x,a,b]); |
| Plot[{y1,y2},{x,a,b}] | plot2d([y1,y2],[x,a,b]); |
| ParametricPlot[{x,y},{t,a,b}] | plot2d([parametric,x,y],[t,a,b]); |
| Plot3D[z,{x,a,b},{y,p,q}] | plot3d(z,[x,a,b],[y,p,q]); |
| ParametricPlot3D[{x,y,z},{s,a,b},{t,p,q}] | plot3d([x,y,z],[s,a,b],[t,p,q]); |
| ListPlot[x] | openplot_curves(x); |
| ◆ 関数定義 | |
| f[x_] := body | f(x) := body |
| define(f(x), body) | |
| f[x_] := Modules[…] | f(x) := block(…) |