定義域を伴った関数の数式処理(jjas 2008)
INOUE Takakatsu 2024-05-11
言語エンジンeng_langの環境設定
HOME <- system("echo ${HOME}", intern=T)
setup_file <- paste(HOME,"/bin/eng_lang_setup.R",sep="")
source(setup_file)## === knitr, (reticulate,) eng_lang are go. ===on3env() : on3ライブラリーのロードとlispファイルの書き出し
batchload("/home/inoue/Maxlib-20/on3lib21.mx")$
on3env()$
max_save()$ /* lisp ファイルに書き出す */## ~/bin/go TMP/tmp_lang/chunk-1.mx > TMP/tmp_lang/chunk-1.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-1.mx")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-1.mx
## batchload("/home/inoue/Maxlib-20/on3lib21.mx")
## on3env()
## -- <on3env> logbegin --
## maxima_tempdir = TMP/tmp_maxima figs_dir = figs
## max_save()
## save("/tmp/max_save.lisp", all)
## "/var/www/html/LANG/TMP/tmp_lang/chunk-1.mx" チャンクの取扱
{skip, echo=T} --- チャンクソースのみ表示
{skip, echo=F} --- チャンクソースを含めて全ての出力を停止
{lang, ext="mxl", eval=T, echo=F} --- チャンク出力のみ表示
{lang, ext="mxl", eval=F, echo=T} --- チャンクソースのみ表示
{lang, ext="mxl", eval=F, echo=F} --- 次の1行のみを表示
*** eval=FALSE ***索引
- 注: 2008年に応用統計学に掲載された内容ですが,その後のプログラムがかなり変更されています。本稿では,プログラム変更に伴い,当時の例題が正しく動作するかを確認する目的で RMarkDown を用いて時々検証しています。以下はその結果です。
定義域を伴った関数の数式処理(jjas 2008)
要旨: 区間(または領域)毎に場合分けされる関数を数式処理言語を用いて記述し, その関数式に対して,微分,積分,等の数式処理を適正に行う為の手法(道具)を提案する. 数式処理言語としては Maxima を用い,結果を Maximaライブラリとしてまとめる. 最後に機能検証の為の使用例を示す.
1 はじめに
区間毎に異なる関数で表される関数を数式処理的に扱う問題を考える. 以下の例を取り上げる. \[ f(x) = \cases{f_1(x) & ($a \leq x < b$~ のとき) \cr f_2(x) & ($b \leq x \leq c$~ のとき) \cr 0 & (その他のとき)} \]
ここで,\(f_1(x),\,f_2(x)\) は三角関数,指数関数,対数関数,等を含みうる一般的な数式表現とする. 上記のような関数表現は統計では一様分布や指数分布といった確率分布や,それらの混合 分布の密度関数, ヒストグラムを経験密度関数として記述する際に現れる.それらの関数は 数値的に取り扱う場合が多いが,数式的に取り扱うことも必要と考えられる. 数式処理言語としては,商用でなく,かつ Windows 版以外に Linux版 が用意されている点を考慮して,Maxima (中川(2002),横田(2006)参照) を用いることにする. 上記の関数 \(f(x)\) を数式処理言語 Maximaで表すと,
f(x) := if a <= x and x < b then f1(x)
else if b <= x and x <= c then f2(x)
else 0 ; のように記述できる. また,上記と同等な機能は Maxima 関数 charfun を用いて
f(x) := f1(x) * charfun('"and", (a <= x, x < b))
+ f2(x) * charfun('"and", (b <= x, x <= c)) ;のように記述できる(バージョン 5.13 以降のcharfun関数では, charfun(a <= x and x < b) のような記述に仕様変更がなされている).それらの記述によって得られた関数式 f(x) では, 定数 \(a,b,c\) に数値を与えた置数後の関数式 f(x) を用いると, そのグラフを描くといった数値評価が行える. しかしながら,どちらの記述においても,関数 f1(x), f2(x) に対しては可能で ある微分,積分といった数式処理操作が,関数式 f(x) に対しては置数 後であっても機能しない.このことは区間によって場合分けされる関数式 f(x) を数式処理的に扱う問題を複雑にする.
本稿では,定義域を記述する Maxima 関数 on3(x, x0, x1, lr) を準備する. 引数は x : 変数, x0 : 左境界値, x1 : 右境界値, lr : 端点の開閉を表す記号 (cc : x0 \(\leq\) x \(\leq\) x1,\(~\) co : x0 \(\leq\) x \(<\) x1,\(~\) oc : x0 \(<\) x \(\leq\) x1,\(~\) oo : x0 \(<\) x \(<\) x1) を表し,
f(x) := f1(x) * on3(x,a,b,co) + f2(x) * on3(x,b,c,cc) ;のように用いることにする. このとき,Maxima 関数 on3 と上記の右辺に現れる関数式(これを on3 関数式と呼ぶ)に幾つかの規則を与え,関数式 f(x) の微分,積分をはじめ,四則演算,2変数関数への対応を可能とするいくつかの Maxima 関数を作成し,それらをまとめ,ライブラリー化する. また,機能検証のための使用例を与える. なお,商用の数式処理言語 Mathematica(バージョン5.1以降)では,高機能な区分定義関数 Piecewise があり,関連関数 PiecewiseExpand を用いて,本稿の後述する on3decomp 関数と同等の処理が可能である.さらに,区分定義関数は Mathematica の標準関数として組み込まれているため,微分,積分といった関数との連携も 良く整備されている. しかしながら,Mathematica の利用環境にないユーザにとって Maxima 上にその代替ツールを 準備すること,および,その作成手順を明らかにすることは重要であると考える.
2 on3 関数の規則
2.1 on3 関数
on3 関数 on3(x,x0,x1,lr) は,変数 \(x\) の値が引数 x0, x1, lr で定まる区間に含まれるとき 関数値「1」を返し,含まれないときは「0」を返す. また,判別不能の場合は定義式を返す. なお,左境界値 x0 として minf(負の無限大),右境界値 x1 として inf(無限大) を指定できるものとする. 以下に実行例を示す.
実行例1
(%i1) on3(0, 1, 3, co); ---> 0
(%i2) on3(1, 1, 3, co); ---> 1
(%i3) on3(3, 1, 3, co); ---> 0
(%i4) on3(inf,0,inf,co); ---> 0
(%i5) on3(x, 1, 3, co); ---> on3(x, 1, 3, co) <--- 判別不能の場合
(%i6) on3(3, 1, b, co); ---> on3(3, 1, b, co) <--- 判別不能の場合
注: ここで,実行結果は ---> のように略記されている.また, <--- は注釈を表す.- Maxima 実行例1
## ~/bin/go TMP/tmp_lang/chunk-3.mxl > TMP/tmp_lang/chunk-3.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl
## on3(0,1,3,co)
## 0
## on3(1,1,3,co)
## 1
## on3(3,1,3,co)
## 0
## on3(inf,0,inf,co)
## 0
## on3(x,1,3,co)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3(3,1,b,co)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-3.mxl"なお,on3 関数 on3(x,x0,x1,lr) の第1引数 x には,変数(アトミック変数)ではなく 一般の式表現を許す.以下に,そのような場合の実行例を示す.
実行例2
(%i1) h(x) := on3(x^2, 1, 4, co)$
(%i2) mshow(h(0), h(1), h(-1), h(2))$ <--- h(0), h(1),... を表示する関数
mshow : h(0) = 0 , h(1) = 1 , h(-1) = 1 and h(2) = 0
(%i3) d(x, y) := on3(sqrt(x^2 + y^2), 2, 3, co)$
(%i4) mshow(d(1, 0), d(1, 1), d(1, 2), d(1, 3))$
mshow : d(1, 0) = 0 , d(1, 1) = 0 , d(1, 2) = 1 and d(1, 3) = 0
(%i5) f(x) := %e^(-x^2) * on3(x^2 , 1, 4, co)$
(%i6) g(x, y) := (x + y + 5) * on3(sqrt(x^2 + y^2), 2, 3, co)$- Maxima 実行例2
## ~/bin/go TMP/tmp_lang/chunk-5.mxl > TMP/tmp_lang/chunk-5.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl
## h(x):=on3(x^2,1,4,co)
## cshow(h(0),h(1),h(-1),h(2))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## d(x,y):=on3(sqrt(x^2+y^2),2,3,co)
## cshow(d(1,0),d(1,1),d(1,2),d(1,3))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## f(x):=%e^-x^2*on3(x^2,1,4,co)
## g(x,y):=(x+y+5)*on3(sqrt(x^2+y^2),2,3,co)
## g1:gr2d(explicit(f(x),x,-5,5))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## g2:gr3d(explicit(g(x,y),x,-2,2,y,-2,2))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## draw([g1,g2],columns = 2,dimensions = [2*500,500],terminal = 'png,
## file_name = "figs/fig-1")
## part: argument must be a non-atomic expression; found g1
## -- an error. To debug this try: debugmode(true);
## "/var/www/html/LANG/TMP/tmp_lang/chunk-5.mxl"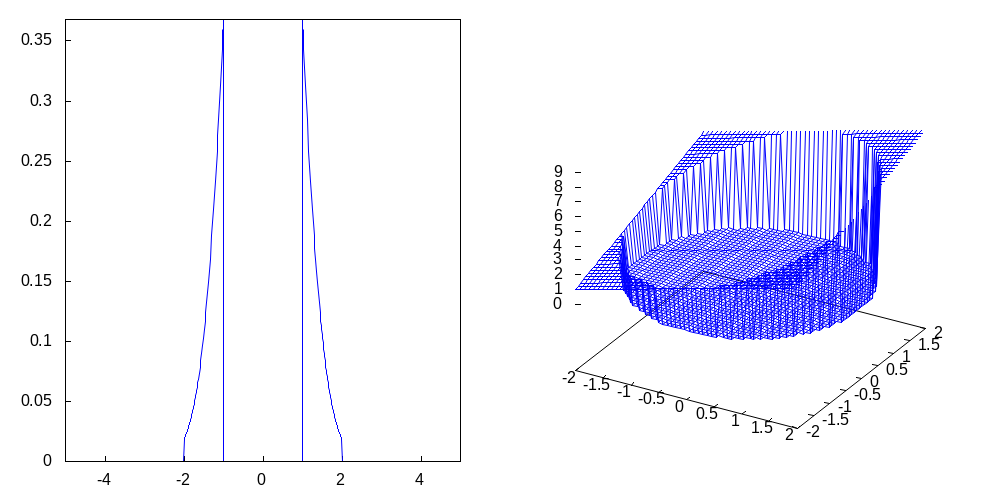
ここで,関数 cshow は1行に複数の評価結果を表示する私用表示関数(ライブラリに含める)である. 上記の実行例での関数 f(x) および g(x,y) をグラフ表示した結果を図\(\ref{fig:1}\)に示す.
実行例2とそのグラフから,on3 関数 on3(x,x0,x1,lr) の第1引数 x に は変数(アトミック変数)ではなく一般式表現を許すが,その利用は数値評価であり,上 記の関数 f(x), g(x,y) を数式レベルで評価する場合は工夫を必要とする.本稿で は,on3 関数 on3(x,x0,x1,lr) の第1引数 x が 変数(アトミック変数)でない場合の取扱いは節3.7 にまとめ,それまでの記述はすべ て,on3 関数の第1引数 x は変数(アトミック変数)とする.
2.2 巾等性
on3関数式に対して以下の規則を与える.すなわち,巾等性をもたせる.
[規則]
f(x) := f1(x) * on3(x,a,b,co);
f(x))^2; ---> (f1(x))^2 * on3(x,a,b,co) 上記の演算規則は本ライブラリの呼び出された時点で常駐化される.
2.3 除法
1個の on3 関数によって構成される関数式の除法(割算)に対して以下の規則を与える.
[規則]
f(x) := f1(x) * on3(x,a,b,co);
1/f(x); ---> 1/f1(x) * on3(x,a,b,co)
g(x) := g1(x) * on3(x,a,b,co);
f(x)/g(x); ---> f1(x)/g1(x) * on3(x,a,b,co)- Maxima 実行例2
f(x) := f1(x) * on3(x,a,b,co)$
cshow(1/f(x))$ /* ---> 1/f1(x) * on3(x,a,b,co) */
g(x) := g1(x) * on3(x,a,b,co)$
cshow(f(x)/g(x))$ /* ---> f1(x)/g1(x) * on3(x,a,b,co) */## ~/bin/go TMP/tmp_lang/chunk-6.mxl > TMP/tmp_lang/chunk-6.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl
## f(x):=f1(x)*on3(x,a,b,co)
## cshow(1/f(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## g(x):=g1(x)*on3(x,a,b,co)
## cshow(f(x)/g(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-6.mxl"f(x)/g(x) を与えると Maxima は内部簡約化により \(\dfrac{\rm on3(x,a,b,co)}{\rm on3(x,a,b,co)} = 1\) と見なし,無意味な結果 \(\dfrac{f1(x)}{f2(x)}\) を返す. そのため,上記の演算規則は常駐化させ,かつ Maxima の内部簡約化の前に適用する.
2.4 乗法
2個(以上)の on3 関数が積の形で現れるときの演算規則を与える.次の例から考える.
f(x) := f1(x) * on3(x,a,b,co) * f2(x) * on3(x,c,d,co); 2つ区間 \([a,b)\),\([c,d)\) (ただし,\(a <b,~c <d\) とする) の位置関係が比較可能なと きには以下のように処理される.
- \(a < b \leq c < d\) のとき \(f(x) = 0\)
- \(a \leq c < b \leq d\) のとき \(f(x) = f1(x) * f2(x) * on3(x,c,b,co)\)
- \(a \leq c < d \leq b\) のとき \(f(x) = f1(x) * f2(x) * on3(x,c,d,co)\)
- \(c \leq a < b \leq d\) のとき \(f(x) = f1(x) * f2(x) * on3(x,a,b,co)\)
- \(c \leq a < d \leq b\) のとき \(f(x) = f1(x) * f2(x) * on3(x,a,d,co)\)
- \(c < d \leq a < b\) のとき \(f(x) = 0\)
\(\displaystyle \prod_{i=1}^{k} \rm f_i(x) * on3(x,\,xl_i,\,xr_i,\,lr)\) の場合にも, 上記の規則を再帰的に機能させる.なお,端点\(a,\,b,\,c,\,d\) のいずれかが文字定数で 上記の区間比較が出来ない場合は定義式を返すものとする. この処理のための関数 on3simp(f(x)) を準備する. 以下に実行例を示す.
実行例3
(%i1) f(x) := f1(x)*on3(x,1,3,co)*f2(x)*on3(x,2,5,co)*f3(x)*on3(x,0,10,co)$
(%i2) on3simp(f(x));
(%o2) f1(x) f2(x) f3(x) on3(x, 2, 3, co)
(%i3) f(x) := f1(x)*on3(x,1,3,co)*f2(x)*on3(x,a,b,co)$
(%i4) on3simp(f(x));
(%o4) f1(x) f2(x) on3(x, 1, 3, co) on3(x, a, b, co)- 実行例3
## ~/bin/go TMP/tmp_lang/chunk-8.mxl > TMP/tmp_lang/chunk-8.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl
## f(x):=f1(x)*on3(x,1,3,co)*f2(x)*on3(x,2,5,co)*f3(x)*on3(x,0,10,co)
## on3simp(f(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## f(x):=f1(x)*on3(x,1,3,co)*f2(x)*on3(x,a,b,co)
## on3simp(f(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/var/www/html/LANG/TMP/tmp_lang/chunk-8.mxl"2.5 加法(減法)
次の様なon3関数式 f(x) を考える.
f(x) := f1(x) * on3(x,a,b,co) + f2(x) * on3(x,c,d,co); ここで,2個のon3関数で定まる区間が互いに排他的(共通部分をもたない)でないとき, これを互いに排他的な区間に分解し,その分解された区間上の関数表現を得ることを考える. そのような分解演算は f(x) の定積分や不定積分関数(確率密度関数のときその分布関数)を求める状況, 等で必要になる. いま,2つ区間 \([a,b)\),, \([c,d)\) ~(ただし,\(a < b,~c <d\) とする) の位置関係が比較可能とすると,以下のような6通り (\(= \frac{4!}{2! \cdot 2!}\)) の場合に分類され,それぞれ以下のように互いに排他的な区間に分解される.
- \(a < b \leq c < d\) のとき \(f(x) = f1(x)*on3(x,a,b,co)+f2(x)*on3(x,c,d,co)\)
- \(a \leq c < b \leq d\) のとき \(f(x) = f1(x)*on3(x,a,c,co)+(f1(x)+f2(x))*on3(x,c,b,co)+f2(x)*on3(x,b,d,co)\)
- \(a \leq c < d \leq b\) のとき \(f(x) = f1(x)*on3(x,a,c,co)+(f1(x)+f2(x))*on3(x,c,d,co)+f1(x)*on3(x,d,b,co)\)
- \(c \leq a < b \leq d\) のとき \(f(x) = f2(x)*on3(x,c,a,co)+(f1(x)+f2(x))*on3(x,a,b,co)+f2(x)*on3(x,b,d,co)\)
- \(c \leq a < d \leq b\) のとき \(f(x) = f2(x)*on3(x,c,a,co)+(f1(x)+f2(x))*on3(x,a,d,co)+f1(x)*on3(x,d,b,co)\)
- \(c < d \leq a < b\) のとき \(f(x) = f1(x)*on3(x,a,b,co)+f2(x)*on3(x,c,d,co)\)
ここで,区間の分解と端点での開閉を判定する必要があるが,上記 2. の場合について例示する.
2. の場合
|
f2(x) | *-----------+
|
f1(x) | *---------+ (*は閉,+は開を表す)
|
------------------------------> x
a c b d上記略図において,端点 \(c\) は左区間 \([a,\,c]\) ではなく右区間 \([c,\,b)\) に含まれる点に 注意する.そのような端点処理(端点が左右何方の区間に含めるかを判定する処理)は, 端点 \(c\) ,端点 \(c\) を右境界値とする左区間の中点 \({\rm ml} = \frac{1}{2}(a+c)\) と,端点 \(c\) を左境界値とする右区間の中点 \({\rm mr} = \frac{1}{2}(c+b)\) での関数式
c : f1(x)*on3(c,a,b,co) + f2(x)*on3(c,c,d,co) = f1(x) + f2(x)
ml : f1(x)*on3(ml,a,b,co) + f2(x)*on3(ml,c,d,co) = f1(x)
mr : f1(x)*on3(mr,a,b,co) + f2(x)*on3(mr,c,d,co) = f1(x) + f2(x)を調べ,端点 c での関数式が右区間の関数式に一致することで右区間に含めると判定する. 次の例を考える.
f(x) := f1(x)*on3(x,a,b,co) + f2(x)*on3(x,c,d,co) + f3(x)*on3(x,e,f,co); このとき,3つ区間 \([a,\,b),~[c,\,d),~[e,\,f)\)~(ただし,\(a < b,~c <d,~e < f\) とする) は \(\frac{6!}{2! \cdot 2! \cdot 2!} = 90\) 個の場合に分類される.同様に4個の区間では,場合の数は \(\frac{8!}{2!^4} = 2520\) となり,場合分けによる方法以外の対応が必要になる.
次の一般例を考える.
f(x) := f1(x) * on3(x,l1,r1,lr1) + f2(x) * on3(x,l2,r2,lr2) + ...
+ fi(x) * on3(x,li,ri,lri) + ... + fk(x) * on3(x,lk,rk,lrk) ; このとき,以下の【手順】を考える.
手順1° 端点 (l1, r1, l2, r2, ..., lk,rk) を要素とするリスト T を作成し,さらに,
minf(負の無限大) と inf(無限大) をリスト要素としてTに追加する.
手順2° リストT = [t1, t2, ...] を t1 <= t2 <= ... となるようにソートを行う.
手順3° ソート後のリスト T から同値要素があれば切り詰め,切り詰め後のリストを T=[t1,t2,...,tm] とする.
(このとき,t1=minf, tm=inf である.)
手順4° リスト T の第1要素 t1=minf と第2要素 t2 を両端とする区間を K1 とし,第2要素 t2 と 第3要素 t3 を両端とする区間を K2 とする.
以下同様にして第(m-1)区間を Km-1 とする.これらの区間の関数式と端点処理を行うために次の関数を準備する.
g(x,t) := f1(x) * on3(t,l1,r1,lr1) + f2(x) * on3(t,l2,r2,lr2) + ...
+ fi(x) * on3(t,li,ri,lri) + ... + fk(x) * on3(t,lk,rk,lrk) ;
また,各区間 Ki の左境界値を tl,右境界値を tr,中央値を tm とする.
このとき,区間 Ki の関数式は g(x,tm) で得られ,端点検査は g(x,tl) = g(x,tm) ならば左境界値 tl を区間 Ki に含め(その他のときは含めない),同様に,g(x,tr) = g(x,tm) ならば右境界値 tr を区間 Ki に含める(その他のときは含めない)ことで行える.
なお,第1区間の左境界値はminfより左開,第(m-1)区間の右境界値はinfより右開となる.
手順5° 上記 4°で得られた各区間の関数式 g(x,tm) と端点検査に基づくon3(x,tl,tr,rl) の積 g(x,tm) * on3(x,tl,tr,rl) の全ての区間に亘る和を構成し,これを結果として返す.なお,関数式 g(x,tm) がゼロとなる無意味な区間は自動的に消滅する. 結果として,区間を「互いに排他的な区間」に分解しそれらの排他的な区間での関数式を明示的 に得ることが出来る.上記の処理を関数 on3decomp(funcs)で行う. 以下に実行例を示す.
実行例4
(%i1) f(x) := f1(x)*on3(x,1,3,co) + f2(x)*on3(x,2,5,cc) + f3(x)*on3(x,0,inf,co)$
(%i2) on3decomp(f(x));
(%o2) f3(x) on3(x, 5, inf, oo) + (f3(x) + f2(x)) on3(x, 3, 5, cc)
+ (f3(x) + f2(x) + f1(x)) on3(x, 2, 3, co)
+ (f3(x) + f1(x)) on3(x, 1, 2, co) + f3(x) on3(x, 0, 1, co)
(%i3) g(x) := g1(x)*on3(x,minf,0,oo) + g2(x)*on3(x,0,inf,oo)
+ g3(x)*on3(x,minf,1,oo) + g4(x)*on3(x,1,inf,oo)$
(%i4) on3decomp(g(x));
(%o4) (g3(x) + g1(x)) on3(x, minf, 0, oo) + (g4(x) + g2(x)) on3(x, 1, inf, oo)
+ g2(x) on3(x, 1, 1, cc) + (g3(x) + g2(x)) on3(x, 0, 1, oo)
+ g3(x) on3(x, 0, 0, cc)- Maxima 実行例4
## ~/bin/go TMP/tmp_lang/chunk-10.mxl > TMP/tmp_lang/chunk-10.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-10.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-10.mxl
## display2d:true
## f(x):=f1(x)*on3(x,1,3,co)+f2(x)*on3(x,2,5,cc)+f3(x)*on3(x,0,inf,co)
## on3decomp(f(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## g(x):=g1(x)*on3(x,minf,0,oo)+g2(x)*on3(x,0,inf,oo)+g3(x)*on3(x,minf,1,oo)
## +g4(x)*on3(x,1,inf,oo)
## on3decomp(g(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-10.mxlなお,節2.4で示した関数 on3simp を on3decomp から呼び出し, on3 関数式の積に対する処理機能を含めることにした. よって,関数 on3simp は主に内部関数として用いられるが,大規模な関数式において 積のみの簡約化結果を眺めたい状況を考慮し,ユーザ関数として残すことにした.
2.6 on3関数式の逆数
互いに排他的な区間に分解された加法表現式に対して以下の演算規則を定める.
g(x) := g1(x) * on3(x,a,b,co) + g2(x) * on3(x,c,d,co);
on3inv(g(x)); ---> 1/g1(x) * on3(x,a,b,co) + 1/g2(x) * on3(x,c,d,co)上記の処理を関数 on3inv(funcs)で行う.以下に実行例を示す.
実行例5
(%i1) f(x) := f2(x) * on3(x, 3, 9, co) + f1(x) * on3(x, 1, 5, co)$
(%i2) g(x) := g2(x) * on3(x, 4, 7, co) + g1(x) * on3(x, 2, 4, co)$
(%i3) gout : on3inv(g(x)); <--- 関数適用
on3(x, 4, 7, co) on3(x, 2, 4, co)
(%o3) ---------------- + ----------------
g2(x) g1(x)
(%i4) fout : on3decomp(f(x)); <--- 関数式f(x)の排他的分解
(%o4) f2(x) on3(x, 5, 9, co) + (f2(x) + f1(x)) on3(x, 3, 5, co)
+ f1(x) on3(x, 1, 3, co)
(%i5) out : ratsimp(on3decomp(fout*gout)); <--- f(x)/g(x) の計算
(%o5) (f2(x) g1(x) on3(x, 5, 7, co)
+ (f2(x) + f1(x)) g1(x) on3(x, 4, 5, co)
+ (f2(x) + f1(x)) g2(x) on3(x, 3, 4, co)
+ f1(x) g2(x) on3(x, 2, 3, co)) / (g1(x) g2(x))
(%i6) on3decomp(f(x)/g(x)); <--- f(x)/g(x) の自動処理
f2(x) on3(x, 5, 7, co) (f2(x) + f1(x)) on3(x, 4, 5, co)
(%o6) ---------------------- + --------------------------------
g2(x) g2(x)
(f2(x) + f1(x)) on3(x, 3, 4, co) f1(x) on3(x, 2, 3, co)
+ -------------------------------- + ----------------------
g1(x) g1(x)- Maxima 実行例5
## ~/bin/go TMP/tmp_lang/chunk-12.mxl > TMP/tmp_lang/chunk-12.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-12.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-12.mxl
## display2d:true
## f(x):=f2(x)*on3(x,3,9,co)+f1(x)*on3(x,1,5,co)
## g(x):=g2(x)*on3(x,4,7,co)+g1(x)*on3(x,2,4,co)
## gout:on3inv(g(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## fout:on3decomp(f(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## out:ratsimp(on3decomp(fout*gout))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3decomp(f(x)/g(x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-12.mxlなお,関数 on3inv(funcs) では,引数 funcs に排他的区間に分解されていない関数式を与えた場合, 自動的に排他的分解を行いその後に上記の演算を行うものとする. この関数規則を用いると,加法形式で記述された2つ関数式 f(x), g(x) に対してその割算 f(x)/g(x) を行うことが出来る. また,f(x)/g(x) のような on3 関数多項式を分母にもつ関数式に対して,これを自動検出し,上記の 分解を与える機能を on3decopmp 関数に付加した.
2.7 on3 関数式の微分
次の on3 関数式 f(x) を変数 x に関して k 階微分した導関数を次式で与える.
f(x) := f1(x) * on3(x,a,b,co) + f2(x) * on3(x,c,d,co);
on3diff(f(x),x,k);
---> diff(f1(x),x,k) * on3(x,a,b,lr) + diff(f2(x),x,k) * on3(x,c,d,lr)Maxima は on3 関数を変数 x を含む関数と見なす.従って,Maxima の微分関数 diff を用いると
{f1(x)*on3(x,...)}' = {f1(x)}'*on3(x,...) + f1(x)*{on3(x,...)}' のように振る舞う.これを阻止し,端点での開閉検査機能をもたせた微分関数 on3diff() を作成する.(実行例6 参照) %なお,Maxima 標準関数 diff での微分規則(偏微分,全微分等の規則)は %そのまま適用される.(実行例6 参照)
2.8 on3 関数式の積分
次の on3 関数式 f(x) を変数 x に関して積分する関数 on3integ() を次式で与える.
規則
f(x) := f1(x) * on3(x,a,b,co) + f2(x) * on3(x,c,d,co);
on3integ(f(x),x); <--- 次の不定積分(関数)を返す
---> (on3decomp による排他的な分解と端点処理機能をもたせる)
on3integ(f(x),x,x0,x1); <--- x0からx1までの定積分値を返す.
---> (on3decomp による排他的な分解とx0,x1の位置を判定し計算する)実行例6
(%i1) f(x) := f1(x)*on3(x,0,1,co) + f2(x)*on3(x,1,inf,co)$
(%i2) f1(x) := x^2$
(%i3) f2(x) := %e^(-(x-1))$
(%i4) f(x);
1 - x 2
(%o4) %e on3(x, 1, inf, co) + x on3(x, 0, 1, co)
(%i5) on3diff(f(x),x,1); <--- f(x) の微分
1 - x
(%o5) 2 x on3(x, 0, 1, oo) - %e on3(x, 1, inf, oo)
(%i6) on3integ(f(x),x); <--- f(x) の不定積分
- x x 3
%e (4 %e - 3 %e) on3(x, 1, inf, oo) x on3(x, 0, 1, cc)
(%o6) --------------------------------------- + -------------------
3 3
(%i7) on3integ(f(x),x,1/2,3/2); <--- f(x) の定積分
31 1
(%o7) -- - --------
24 sqrt(%e)
(%i8) define(F(x), on3integ(f(x),x))$ <--- 不定積分関数の定義
(%i9) ratsimp(F(3/2) - F(1/2)); <--- 不定積分関数を用いた定積分
31 sqrt(%e) - 24
(%o9) ----------------
24 sqrt(%e)- Maxima 実行例6
## ~/bin/go TMP/tmp_lang/chunk-14.mxl > TMP/tmp_lang/chunk-14.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-14.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-14.mxl
## display2d:true
## f(x):=f1(x)*on3(x,0,1,co)+f2(x)*on3(x,1,inf,co)
## f1(x):=x^2
## f2(x):=%e^-(x-1)
## "/* <--- f(x) の微分 */"
## on3diff(f(x),x,1)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/* <--- f(x) の定積分 */"
## on3integ(f(x),x,1/2,3/2)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/* <--- 不定積分関数の定義 */"
## define(F(x),on3integ(f(x),x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## "/* <--- 不定積分関数を用いた定積分 */"
## ratsimp(F(3/2)-F(1/2))
## 3 1
## F(-) - F(-)
## 2 2
## /var/www/html/LANG/TMP/tmp_lang/chunk-14.mxlなお,不定積分が返す関数 \(F(x)\) は,任意定数 \(x_0,\,x_1\) (すなわち, \(x_0\) と \(x_1\) とが異なる区間内の点であることを許す)に対して \(\displaystyle \int_{x_0}^{x_1} f(x)\,dx = F(x_1) - F(x_0)\) を満たすように積分定数が決められている.よって,\(f(x)\) が確率密度関数で あれば,不定積分関数 \(F(x)\) は分布関数となる. 以下に実行例を示す.
2.9 on3関数式の求解
on3 関数式 f(x) に関して,方程式 f(x) = 0 を求める関数 on3solve を作成した.以下に実行例を示す.
実行例7
(%i1) eq : -1/8*on3(x,minf,inf,oo) + x^2*on3(x,minf,0,oo)
+ (1-x)*on3(x,1,inf,oo) + (1-x)*(1+x)/2*on3(x,0,1,oo)$
(%i2) on3solve(eq, [x]);
1 sqrt(3)
(%o2) [x = - ---------, x = -------]
2 sqrt(2) 2- Maxima 実行例7
## ~/bin/go TMP/tmp_lang/chunk-15.mxl > TMP/tmp_lang/chunk-15.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-15.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-15.mxl
## display2d:true
## eq:((-1)/8)*on3(x,minf,inf,oo)+x^2*on3(x,minf,0,oo)+(1-x)*on3(x,1,inf,oo)
## +(((1-x)*(1+x))/2)*on3(x,0,1,oo)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3solve(eq,[x])
## length: argument cannot be a symbol; found out
## #0: on3solve(args=[eq,[x]])
## -- an error. To debug this try: debugmode(true);
## /var/www/html/LANG/TMP/tmp_lang/chunk-15.mxl2.10 on3関数式のリスト表現化
次の on3 関数式 f(x) を対応するリスト形式に変換する関数 on3list を作成する.
規則
f(x) := f1(x) * on3(x,a,b,co) + f2(x) * on3(c,d,co) + ... ;
L : on3list(f(x));
---> [[f1(x),[x,a,b,co]], [f2(x),[x,c,d,co]], ... ]このような処理関数は定義域部の集合演算的処理だけでなく,関数部 f1(x), f2(x), … に対してより複雑な数式処理を指定する際に必要となる. %%%(この機能を Maxima 言語を用いて実現できることに気付くのに筆者は苦慮した.) 前述のon3decomp, on3integ関数等はこの機能を用いて作成された. なお,リスト L において L[1] は [f1(x),[x,a,b,co]] を返し,L[1][1] は f1(x) を返す.
2.11 リスト化された関数式のon3関数表現化
on3list 関数によってリスト化された内容を on3 関数式に変換する関数 on3funcを次式で定める.
規則
L : [[f1(x),[x,a,b,co]], [f2(x),[x,c,d,co]], ... ];
on3func(L);
---> f1(x) * on3(x,a,b,co) + f2(x) * on3(c,d,co) + ...3 on3 関数の2変数関数式への拡張
本節では前節で与えた on3 関数式 f(x) を次のような2変数関数式 f(x,y) に拡張する.
f(x,y) := f1(x,y) * on3(x,x0,x1,co) * on3(y,y0,y1,co) + ...すなわち,\(D = \{(x,\,y), x_0 \leq x < x_1,\, y_0 \leq y < y_1\}\) (矩形領域)を定義域とす る2変数関数 \(f(x,\,y)\) に関して前節と同様な操作を考える. 以下では,そのために拡張された部分について述べる.
3.1 on3 関数式のリスト表現化
規則
f(x,y) := f1(x,y) * on3(x,x0,x1,co) * on3(y,y0,y1,co) + ... ;
on3list(f(x,y));
---> [[f1(x,y),[x,x0,x1,co,y,y0,y1,co]], ... ]3.2 リスト化された関数式の on3 関数表現化
規則
L : [[f1(x,y),[x,x0,x1,co,y,y0,y1,co]], ... ];
on3func(L);
---> f1(x,y) * on3(x,x0,x1,co) * on3(y,y0,y1,co) + ...3.3 on3decomp 関数の拡張
on3list 関数によってリスト化された表現を用いて,領域定義変数の検出,検出 された変数に基づく互いに排他的な領域(矩形領域)への分割とその領域上の関 数式の導出,端点検査を行うように機能拡張し,これを改めて on3decomp 関数とした.
また,分割された排他的な領域を整理する簡約化機能(デフォルトで実行)をも たせ,その機能を使用しない場合は引数 noreduce を指定するようにした. 以下に実行例を示す.
実行例8
(%i1) f(x,y) := f1(x,y)*on3(x,3,7,co)*on3(y,4,8,co)
+ f2(x,y)*on3(x,1,5,co)*on3(y,2,6,co)$
(%i2) on3decomp(f(x,y),noreduce); <--- 領域に関する簡約化を用いない場合
(%t2) vars = [x, y] <--- on3 関数に現れた変数を表示
(%o2) on3(x, 5, 7, co) f1(x, y) on3(y, 6, 8, co)
+ on3(x, 3, 5, co) f1(x, y) on3(y, 6, 8, co)
+ on3(x, 3, 5, co) (f2(x, y) + f1(x, y)) on3(y, 4, 6, co)
+ on3(x, 1, 3, co) f2(x, y) on3(y, 4, 6, co)
+ on3(x, 5, 7, co) f1(x, y) on3(y, 4, 6, co)
+ on3(x, 3, 5, co) f2(x, y) on3(y, 2, 4, co)
+ on3(x, 1, 3, co) f2(x, y) on3(y, 2, 4, co)
(%i3) on3decomp(f(x,y)); <--- 領域に関する簡約化を用いる(デフォルト)場合
(%t3) vars = [x, y]
(%o3) on3(x, 3, 5, co) f1(x, y) on3(y, 6, 8, co)
+ on3(x, 5, 7, co) f1(x, y) on3(y, 4, 8, co)
+ on3(x, 3, 5, co) (f2(x, y) + f1(x, y)) on3(y, 4, 6, co)
+ on3(x, 1, 3, co) f2(x, y) on3(y, 2, 6, co)
+ on3(x, 3, 5, co) f2(x, y) on3(y, 2, 4, co)- Maxima 実行例8 2022.02.16 change
## ~/bin/go TMP/tmp_lang/chunk-16.mxl > TMP/tmp_lang/chunk-16.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-16.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-16.mxl
## display2d:true
## f(x,y):=f1(x,y)*on3(x,3,7,co)*on3(y,4,8,co)+f2(x,y)*on3(x,1,5,co)*on3(y,2,6,co)
## out1:on3decomp21(f(x,y),y)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## out2:on3decomp21(out1,x)
## ◆◆◆ Error in progn = <on3decomp21>
## out1
## out3:on3info(out2,'std)
## out1
## /var/www/html/LANG/TMP/tmp_lang/chunk-16.mxl3.4 on3integ 関数
2変数関数 f(x,y) に関する積分に関しては以下の演算をサポートする.
規則
f(x,y) := f1(x,y) * on3(x,x0,x1,co) * on3(y,y0,y1,co) + ... ;
on3integ(f(x,y),x); <--- 変数xに関する不定積分
on3integ(f(x,y),x,xl,xr); <--- 変数xに関するxlからxrまでの定積分
---> integrate(f1(x,y),x,xl,xr) * on3(x,x0,x1,co) * on3(y,y0,y1,co) + ... これにより,f(x,y) を2変量確率密度関数や2変量ヒストグラムと見なすと,条件付き密度関数,周辺密度関数を求めることが出来る.
3.5 on3solve 関数
2変数関数 f(x,y) に関する方程式を解く.以下に実行例を示す.
実行例9
(%i1) eq1 : (x^2 + x*y -1) * on3(x,0,inf,co) * on3(y, 0, inf, co)$
(%i2) eq2 : (x*y^2 - x + y) * on3(x,0,inf,co) * on3(y, minf, inf, oo)$
(%i3) on3solve([eq1, eq2], [x, y]);
sqrt(2 - sqrt(2))
(%o3) [[x = sqrt(2 - sqrt(2)), y = -----------------]]
sqrt(2)- Maxima 実行例9
## ~/bin/go TMP/tmp_lang/chunk-17.mxl > TMP/tmp_lang/chunk-17.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-17.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-17.mxl
## display2d:true
## eq1:(x^2+x*y-1)*on3(x,0,inf,co)*on3(y,0,inf,co)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## eq2:(x*y^2-x+y)*on3(x,0,inf,co)*on3(y,minf,inf,oo)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3solve([eq1,eq2],[x,y])
## length: argument cannot be a symbol; found out
## #0: on3solve(args=[[eq1,eq2],[x,y]])
## -- an error. To debug this try: debugmode(true);
## /var/www/html/LANG/TMP/tmp_lang/chunk-17.mxl3.6 変数変換に伴う領域変換
on3(x,x0,x1,co) * on3(y,y0,y1,co) で定まる領域 \(D= \{(x,\,y); \,x_0 \leq x < x_1,\,y_0 \leq y < y_1\}\) を変数変換 \(t = x + y,\, u = y\) を用いて変換した \((t,\,u)\) の領域を \(G = \{(t,\,u); \,t_0 \leq t < t_1,\,u_0(t) \leq u < u_1(t)\}\) の形式で返す関数 on3chgvar2 を用意する. これまでと同様に,x0, y0 には minf を,x1, y1 には inf を指定でき,開閉の指定も可能とする. 以下に実行例を示す.
実行例10
(%i1) ex1 : on3(x, 0, 1, co) * on3(y, 0, 1, co)$
(%i2) on3chgvar2(ex1);
(%o2) on3(t, 1, 2, co) on3(u, t - 1, 1, cc) + on3(t, 0, 1, co) on3(u, 0, t, cc)
(%i3) ex2 : on3(x,0,1,co) * on3(y,0,2,co)$
(%i4) on3chgvar2(ex2);
(%o4) on3(t, 1, 2, co) on3(u, t - 1, t, cc)
+ on3(t, 2, 3, co) on3(u, t - 1, 2, cc)
+ on3(t, 0, 1, co) on3(u, 0, t, cc)
(%i5) ex3 : on3(x,0,2,co) * on3(y,0,1,co)$
(%i6) on3chgvar2(ex3);
(%o6) on3(t, 2, 3, co) on3(u, t - 2, 1, cc)
+ on3(t, 0, 1, co) on3(u, 0, t, cc)
+ on3(t, 1, 2, co) on3(u, 0, 1, cc)
(%i7) ex4 : on3(x, 0, inf, co) * on3(y, 0, inf, co)$
(%i8) on3chgvar2(ex4);
(%o8) on3(t, 0, inf, co) on3(u, 0, t, cc)- Maxima 実行例10
## ~/bin/go TMP/tmp_lang/chunk-18.mxl > TMP/tmp_lang/chunk-18.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-18.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-18.mxl
## ex1:on3(x,0,1,co)*on3(y,0,1,co)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3chgvar2(ex1)
## length: argument cannot be a symbol; found ex1
## #0: on3chgvar2(args=[ex1])
## -- an error. To debug this try: debugmode(true);
## "/var/www/html/LANG/TMP/tmp_lang/chunk-18.mxl"3.7 on3 関数の非アトミック変数への対応
節2.1 において,on3 関数 on3(x,x0,x1,lr) の第1引数 x には変数(ア トミック変数)ではなく,一般の式表現を許すことを示した.しかしながら,on3 関数 式の数値的取扱いは別として,その数式レベルの取扱いにおいては注意を払う必要がある. そのため,節2.2以降の記述はすべてアトミック変数の場合を取り扱ってきた.本節で は,on3 関数の第1引数が非アトミック変数の場合を取り上げる.はじめに,on3 関数の 第1引数が1変数関数(1個のアトミック変数の関数)で表せる場合について述べる.以下 に実行例を示す.
実行例11
(%i1) on3(x^2, 1, 4, co, eval); <--- 第1例
(%o1) on3(x, 1, 2, co) + on3(x, - 2, - 1, oc)
(%i2) on3(log(x), 1, 2, cc, eval); <--- 第2例
2
(%o2) on3(x, %e, %e , cc)- Maxima 実行例11
## ~/bin/go TMP/tmp_lang/chunk-19.mxl > TMP/tmp_lang/chunk-19.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-19.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-19.mxl
## display2d:true
## on3(x^2,1,4,co,eval)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3(log(x),1,2,cc,eval)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-19.mxlすなわち,on3 関数の第1引数が1変数関数で表せる場合には,on3 関数の最後にオプ ション引数 eval を追加することにより,アトミック変数に関する on3 関数式 を返すように機能拡張する.本機能は第1例について述べると,第1引数からアトミック 変数を見出し,方程式 \(x^2=1\) や \(x^2=4\) を変数\(x\)に ついて解く機能と,それらの解と minf , inf を端点とする各区間の 初与の on3 関数式に基づく端点検査機能により得られる. 方程式の求解に関しては, Maxima の標準関数 solve を用い,これに失敗した場合は realroots 関数を用いるようにした. また,本機能は,on3decomp にも組み込むようにした. この拡張機能を用いることにより,本稿の節2.2 から前節までの on3 関連関数を用い ることができる.次に,on3 関数の第1引数が2変数関数(2個のアトミック変数の関数) で表せる場合について考える.この場合には,一般の2次元領域における有効な 排他的領域分割の方法が見い出せない.よって,手動による対応が必要になる.以下にそ のような実行例を2例示す.実行例12a は累次積分によるアプローチであり,実行例 12b は極座標変換によるアプローチである.なお,取り上げた2変数関数 z0(x,y) は節2.1の図1の右図に示されている.
実行例12a
(%i1) z0(x, y) := (x + y + 5) * on3(x^2 + y^2, 4, 9, cc)$
(%i2) ans1 : solve(x^2 + y^2 = 4, [y]); <--- 条件式をyについて解く
2 2
(%o2) [y = - sqrt(4 - x ), y = sqrt(4 - x )]
(%i3) ans2 : solve(x^2 + y^2 = 9, [y]); <--- 条件式をyについて解く
2 2
(%o3) [y = - sqrt(9 - x ), y = sqrt(9 - x )]
(%i4) define(y1(x), rhs(ans1[2])); <--- 領域設定に用いる関数y1(x)を定義
2
(%o4) y1(x) := sqrt(4 - x )
(%i5) define(y2(x), rhs(ans2[2]));
2
(%o5) y2(x) := sqrt(9 - x ) <--- 領域設定に用いる関数y2(x)を定義
(%i6) assume(9 - x^2 > 0 and 4 - x^2 > 0)$ <--- 仮定の設定
(%i7) z1(x, y) := (x + y + 5) *
( on3(x, 2, 3, cc) * on3(y, -y2(x), y2(x), cc)
+ on3(x, -2, 2, co) * on3(y, y1(x), y2(x), cc)
+ on3(x, -2, 2, co) * on3(y, -y2(x), -y1(x), cc)
+ on3(x, -3, -2, co) * on3(y, -y2(x), y2(x), cc) )$
<--- 累次積分形式で定義域を手動で設定する
(%i8) out : ratsimp(on3integ(on3integ(z1(x, y), y, minf, inf),
x, minf,inf)); <--- 2重積分
on3integ : 2変数 定積分
(%o8) 25 %pi <--- 結果- Maxima 実行例12a
## ~/bin/go TMP/tmp_lang/chunk-20.mxl > TMP/tmp_lang/chunk-20.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-20.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-20.mxl
## display2d:true
## on3(x^2,1,4,co,eval)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## on3(log(x),1,2,cc,eval)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## z0(x,y):=(x+y+5)*on3(x^2+y^2,4,9,cc)
## ans1:solve(x^2+y^2 = 4,[y])
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## ans2:solve(x^2+y^2 = 9,[y])
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## define(y1(x),rhs(ans1[2]))
## y1(x) := 0
## define(y2(x),rhs(ans2[2]))
## y2(x) := 0
## assume(9-x^2 > 0 and 4-x^2 > 0)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## z1(x,y):=(x+y+5)
## *(on3(x,2,3,cc)*on3(y,-y2(x),y2(x),cc)+on3(x,-2,2,co)*on3(y,y1(x),y2(x),cc)
## +on3(x,-2,2,co)*on3(y,-y2(x),-y1(x),cc)
## +on3(x,-3,-2,co)*on3(y,-y2(x),y2(x),cc))
## out:ratsimp(on3integ(on3integ(z1(x,y),y,minf,inf),x,minf,inf))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-20.mxl実行例 12b
(%i1) z0(x, y) := (x + y + 5) * on3(x^2 + y^2 , 4, 9, cc)$
(%i2) (x : r * cos(t), y : r * sin(t))$ <--- 極座標変換
(%i3) assume(r > 0)$ <--- 仮定の設定
(%i4) matchdeclare(t_, true)$ <--- 規則定義変数を設定
(%i5) tellsimp(sin(t_)^2, 1 - cos(t_)^2)$ <--- 置換規則の定義
(%i6) ans1 : solve(x^2 + y^2 = 4, [r]);
(%o6) [r = - 2, r = 2]
(%i7) ans2 : solve(x^2 + y^2 = 9, [r]);
(%o7) [r = - 3, r = 3]
(%i8) r1 : rhs(ans1[2]);
(%o8) 2
(%i9) r2 : rhs(ans2[2]);
(%o9) 3
(%i10) z1(r, t) := (x + y + 5) * r * on3(r, r1, r2, cc) * on3(t, 0, 2*%pi, cc)$
<--- 極座標変換後の被積分関数( 右辺の最初に現れる r はヤコビアンを示す)
(%i11) on3integ(on3integ(z1(r, t), t, 0, inf), r, r1, r2);
(%t11) vars = [r, t]
on3integ : 2変数 定積分
(%o11) 25 %pi <--- 結果- Maxima 実行例12b <- on3integ()ではダメ
## ~/bin/go TMP/tmp_lang/chunk-21.mxl > TMP/tmp_lang/chunk-21.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-21.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-21.mxl
## display2d:true
## z0(x,y):=(x+y+5)*on3(x^2+y^2,4,9,cc)
## (x:r*cos(t),y:r*sin(t))
## assume(r > 0)
## matchdeclare(t_,true)
## tellsimp(sin(t_)^2,1-cos(t_)^2)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## ans1:solve(x^2+y^2 = 4,[r])
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## ans2:solve(x^2+y^2 = 9,[r])
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## r1:rhs(ans1[2])
## 0
## r2:rhs(ans2[2])
## 0
## z1(r,t):=(x+y+5)*r*on3(r,r1,r2,cc)*on3(t,0,2*%pi,cc)
## on3integ19(on3integ19(z1(r,t),t,0,inf),r,r1,r2)
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-21.mxl上記の実行例から判るように,2次元領域を定義域にもつ関数(の2重積分)では,変数変 換や累次積分を念頭においた排他的領域分割が必要になる.しかしながら,これを自動化する為の 有効な手段が見い出せず個別対応となっている. 節3.6の on3chgvar2 は変数変換を限定した場合の排他的領域分割を与える例題的関数である.
4 使用例
前節までに作成されたon3関数と一連の関数をライブラリー化し load(“on3lib.mx”) として呼び出すことにする.また,ヘルプ関数 on3help() を用意する(実行例 13 参照). 次に,それらの関数が有効に機能するかを検証するための使用例を実行例 14 に示す.
実行例13
$ maxima <--- Maxima の起動
Run: exec /usr/bin/maxima
Maxima 5.13.0 http://maxima.sourceforge.net
Using Lisp CLISP 2.39 (2006-07-16)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bug_report()
provides bug reporting information.
(%i1) load("on3lib.mx")$ <--- ライブラリの呼出
(%i2) on3help()$ <--- on3help の実行
=== on3lib.mx (定義域を伴った関数の数式操作) 一覧 ===
0. on3help() : on3関数の機能一覧
1. on3(z,z0,z1,lr,[args]) : on3関数(関数定義域)の定義[変数,下限,上限,開閉]
2. on3simp(on3funcs) : on3関数式の積に関する簡約化
3. on3decomp(funcs,[args]) : [1,2変数のみ対応版]
on3関数式の和(差)において排他的な区間(領域)への分解表現を与える
4 on3inv(func) : 1/(f1*on3+f2*on3)--->(1/f1)*on3+(1/f2)*on3
5. on3list(on3funcs) : on3関数式をon3リスト形式に変換する[1,2変数対応版]
6. on3func(on3list) : on3リスト形式をon3関数形式に変換する[1,2変数対応版]
7. on3solve(funcs,[var]) : on3関数方程式の求解[1,2変数対応版]
8. on3diff(func,var,p) : on3関数式の微分(多変数まで対応)
9. on3integ(func,var,[args]) : on3関数式の積分[1,2変数対応版]
on3integ(func,var) : 不定積分関数(分布関数に対応)
on3integ(func,var,x0,x1) : 定積分値
10. on3chgvar2(funcs) : on3関数式f(x,y)を変換(t=x+y,u=y)した関数g(t,u)を返す
11.on3show(funcs) : on3関数式の表示関数[1,2変数対応版]
12. on3pw(funcs) : on3関数式のカプセル化
ex. on3_intro(), on3_ex(), on3simp_ex(), on3inv_ex(),
on3list_ex(), on3func_ex(), on3decomp_ex(), on3show_ex(),
on3diff_ex(), on3integ_ex(), on3solve_ex(), on3chgvar2_ex(),
on3dim2_uni2() : 一様分布に従う独立確率変数の和の分布
on3dim2_exp2() : 指数分布に従う独立確率変数の和の分布
on3test() : on3_ex, on3list_ex, on3simp_ex, on3decomp_ex の連続実行
---> 関数表示 dispfun(on3,on3simp,...) または grind(on3)- Maxima 実行例13
## ~/bin/go TMP/tmp_lang/chunk-22.mx > TMP/tmp_lang/chunk-22.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-22.mx")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-22.mx
## batchload("/home/inoue/Maxlib-20/on3lib21.mx")
## on3help()
## === on3lib.mx (定義域を伴った関数の数式操作) 一覧 ===
## 0. on3help() : on3関数の機能一覧
## 1. on3(z,z0,z1,arg) : on3関数(関数定義域)の定義[変数,下限,上限,開閉]
## 2. f2l(on3funcs) : on3関数式をon3リスト形式に変換する[多変数対応版]
## 3. l2f(on3list) : on3リスト形式をon3関数形式に変換する[多変数対応版]
## 4. on3simp(on3funcs) : on3関数式の積に関する簡約化(on3decompに組み込み)
## 5. on3decomp(funcs,[args]) : [多変数対応版]
## on3関数式の和(差)において素な区間(領域)への分解表現を与える
## 6. on3std(on3func) : on3一般式の標準化
## 7. on3ev(on3func,arg) : 関数部に{factor,ratsimp,expand}を作用する
## 8. on3solve(funcs,vars) : on3関数式の求解[多変数対応版]
## 9. on3diff(func,var,p) : on3関数式の微分[多変数対応版]
## 10. on3integ(func,var,[args]) : on3関数式の積分[多変数対応版]
## on3integ(func,var) : 不定積分関数(分布関数に対応)
## on3integ(func,var,x0,x1) : 定積分値
## 11. on3chgvar2(funcs) : on3関数式f(x,y)を変換(t=x+y,u=y)した関数g(t,u)を返す
## 12. on3show(funcs) : on3関数式の表示[多変数対応版]
##
## 13. on3pw(funcs) : on3関数式のカプセル化
## ex. on3_ex(), on3simp_ex(), on3std_ex(),
## on3decomp_ex(), on3show_ex(), on3ev_ex(),
## on3diff_ex(), on3integ_ex(), on3solve_ex(),
## on3chgvar2_ex() on3pw_ex(),
## ex. on3dim2_uni2() : 一様分布に従う独立確率変数の和の分布
## on3dim2_exp2() : 指数分布に従う独立確率変数の和の分布
## ex. on3test() : on3_ex, on3list_ex, on3simp_ex, on3decomp_ex の連続実行
## ---> 関数表示 dispfun(on3,on3simp,...) または grind(on3)
## /var/www/html/LANG/TMP/tmp_lang/chunk-22.mx以下に,一様分布 \({\rm U}[0,\,1]\) に従う独立確率変数の和の分布(密度関数)を求める問題を例示する.
実行例14
(%i1) load("on3lib.mx")$
(%i2) f1(x) := 1*on3(x,0,1,cc)$ <--- 一様分布の密度関数を定義する
(%i3) g(x,y) := f1(x)*f1(y)$ <--- (x,y) の同時密度関数
(%i4) h2(t,u) := on3chgvar2(g(x,y))$ <--- (t=x+y,u=y) の同時密度関数
(%i5) ldisplay(h2(t,u))$ <--- 関数 h2(t,u) を表示する
(%o5) h2(t, u) = on3(t, 1, 2, co) on3(u, t - 1, 1, cc)
+ on3(t, 0, 1, co) on3(u, 0, t, cc)
(%i6) define(f2(t), on3integ(h2(t,u),u,minf,inf))$ /* 周辺分布 */
<--- h2(t,u) を u に関して定積分を行い tの周辺密度関数を得る
結果(2個の和の密度関数)を関数 f2(t) として定義する
(%i7) ldisplay(f2(t))$ <--- 結果を表示する
(%o7) f2(t) = (2 - t) on3(t, 1, 2, co) + t on3(t, 0, 1, co)
(%i8) g3(x,y) := f2(x)*f1(y)$ <--- 3個の和の分布
(%i9) h3(t,u) := on3chgvar2(g3(x,y))$ /* 同時分布 */
(%i10) ldisplay(h3(t,u))$
(%o10) h3(t, u) = on3(t, 1, 2, co) (t - u) on3(u, t - 1, 1, cc)
+ on3(t, 2, 3, co) (u - t) on3(u, t - 2, 1, cc)
+ 2 on3(t, 2, 3, co) on3(u, t - 2, 1, cc)
+ on3(t, 0, 1, co) (t - u) on3(u, 0, t, cc)
+ on3(t, 1, 2, co) (u - t) on3(u, 0, t - 1, cc)
+ 2 on3(t, 1, 2, co) on3(u, 0, t - 1, cc)
(%i11) out : on3integ(h3(t,u),u,minf,inf)$ /* 周辺分布 */
(%i12) define(f3(t), ratsimp(expand(out),on3))$
(%i13) ldisplay(f3(t))$
2
(%o13) f3(t) = ((t - 6 t + 9) on3(t, 2, 3, co)
2 2
+ (- 2 t + 6 t - 3) on3(t, 1, 2, co) + t on3(t, 0, 1, co))/2
(%i14) g4(x,y) := f2(x)*f2(y)$ <--- 4個の和の分布
(%i15) h4(t,u) := on3chgvar2(g4(x,y))$ /* 同時分布 */
(%i16) out : on3integ(h4(t,u),u,minf,inf)$ /* 周辺分布 */
(%i17) define(f4(t), ratsimp(expand(out),on3))$
(%i18) ldisplay(f4(t))$
3 2
(%o18) f4(t) = - ((t - 12 t + 48 t - 64) on3(t, 3, 4, co)
3 2
+ (- 3 t + 24 t - 60 t + 44) on3(t, 2, 3, co)
3 2 3
+ (3 t - 12 t + 12 t - 4) on3(t, 1, 2, co) - t on3(t, 0, 1, co))/6
(%i19) g5(x,y) := f3(x)*f2(y)$ <--- 5個の和の分布
(%i20) h5(t,u) := on3chgvar2(g5(x,y))$ /* 同時分布 */
(%i21) out : on3integ(h5(t,u),u,minf,inf)$ /* 周辺分布 */
(%i22) define(f5(t), ratsimp(expand(out),on3))$
(%i23) ldisplay(f5(t))$
4 3 2
(%o23) f5(t) = ((t - 20 t + 150 t - 500 t + 625) on3(t, 4, 5, co)
4 3 2
+ (- 4 t + 60 t - 330 t + 780 t - 655) on3(t, 3, 4, co)
4 3 2
+ (6 t - 60 t + 210 t - 300 t + 155) on3(t, 2, 3, co)
4 3 2
+ (- 4 t + 20 t - 30 t + 20 t - 5) on3(t, 1, 2, co)
4
+ t on3(t, 0, 1, co))/24
(%i24) set_plot_option([plot_format,gnuplot])$ <--- 作図準備
(%i25) set_plot_option([gnuplot_term, png])$
(%i27) set_plot_option([gnuplot_out_file, "on3fig-31.png"])$
(%i28) gpreamble : sconc("set xlabel 't'; ", "set yrange [0:1.5]; ")$
(%i29) plot2d(f2(t),[t,-1,3],[gnuplot_preamble, gpreamble]); <--- 作図
(%i30) set_plot_option([gnuplot_out_file, "on3fig-21.png"])$
(%i31) gpreamble : sconc("set xlabel 't'; ", "set ylabel 'u'; ")$
(%i32) plot3d(h2(t,u),[t,-1,3],[u,-1,3],['grid, 100, 60], <--- 作図
[gnuplot_pm3d, true],
[gnuplot_preamble, gpreamble]);
(%i32) quit()$- Maxima 実行例14
#grind(on3dim2_uni2);
on3dim2_uni2('plot, 'noview);## ~/bin/go TMP/tmp_lang/chunk-23.mxl > TMP/tmp_lang/chunk-23.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-23.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-23.mxl
## incorrect syntax: # is not a prefix operator
## #
## ^
## "/var/www/html/LANG/TMP/tmp_lang/chunk-23.mxl"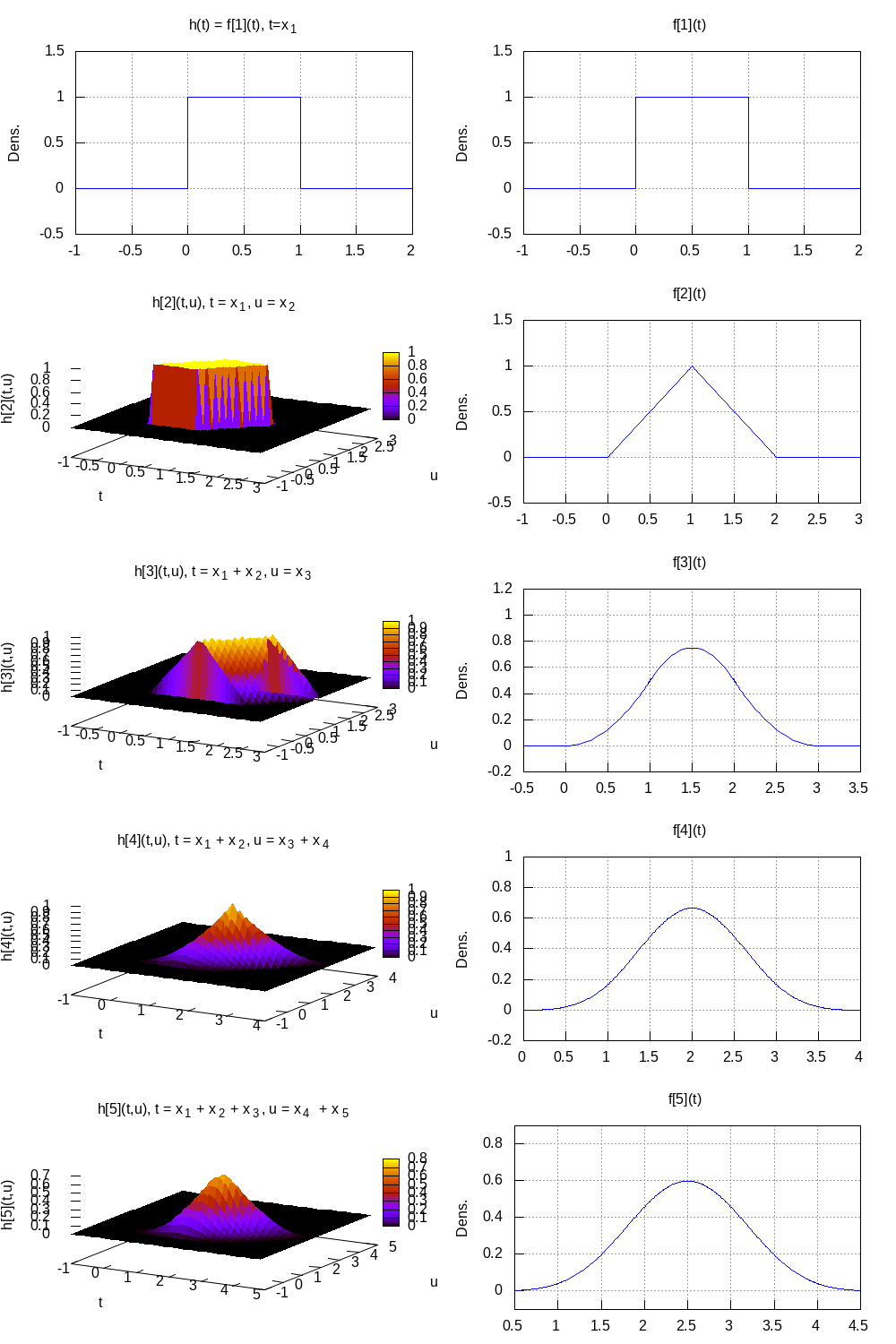
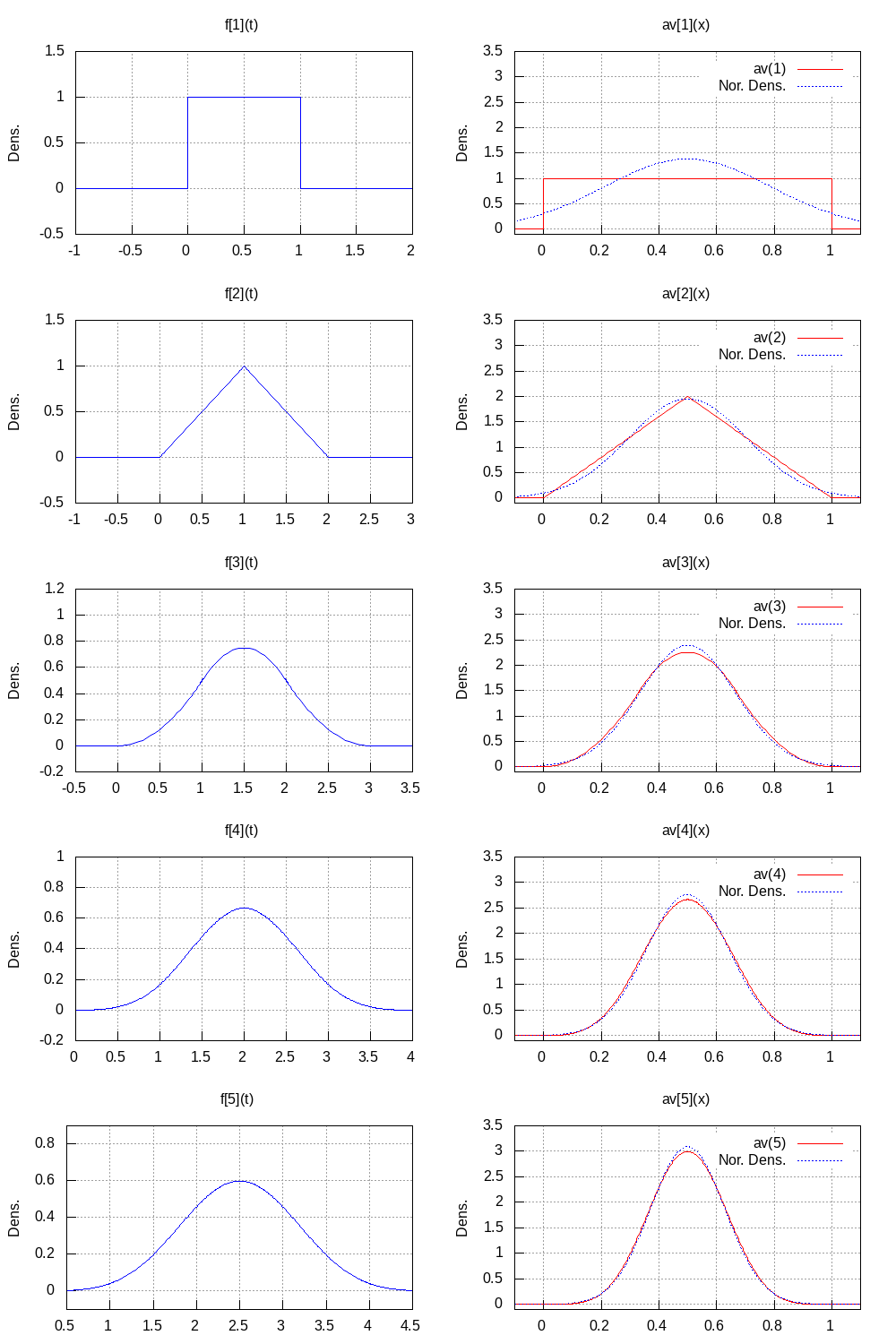
上記の実行例で得た関数 h2(t,u), h5(t,u) のグラフを図ref{fig:2} に, 関数 f2(t), f5(t) のグラフを図ref{fig:3} に示す.
本節の最後に,節3.3の実行例8にあるような表示を少しでも見やすくする表示関数(試作版) on3show の使用例を実行例 15 に示す.
実行例15
(%i1) f(x,y) := f1(x,y)*on3(x,3,7,co)*on3(y,4,8,co)
+ f2(x,y)*on3(x,1,5,co)*on3(y,2,6,co)$
(%i2) on3show(on3decomp(f(x,y),list))$
(%t2) vars = [x, y]
on3decomp(f(x, y), list) =
[ f2(x, y) (1 <= x < 3) & (2 <= y < 6), ]
[ f2(x, y) (3 <= x < 5) & (2 <= y < 4), ]
[ f2(x, y) + f1(x, y) (3 <= x < 5) & (4 <= y < 6), ]
[ f1(x, y) (3 <= x < 5) & (6 <= y < 8), ]
[ f1(x, y) (5 <= x < 7) & (4 <= y < 8), ]
[ 0 ( otherwise ) ]- Maxima 実行例15
## ~/bin/go TMP/tmp_lang/chunk-24.mxl > TMP/tmp_lang/chunk-24.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-24.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-24.mxl
## display2d:true
## f(x,y):=f1(x,y)*on3(x,3,7,co)*on3(y,4,8,co)+f2(x,y)*on3(x,1,5,co)*on3(y,2,6,co)
## on3show(on3decomp(f(x,y),list))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## /var/www/html/LANG/TMP/tmp_lang/chunk-24.mxlon3 関数式のカプセル化への試み
前節までは,定義域を伴った関数を on3 関数式で記述し,その四則演算や微分, 積分,等の数式処理を行い,結果を on3 関数式で返す処理について述べた.本 節では,上記処理結果として得られる on3 関数式以外に一般の関数式が混在す る状況での微分,積分といった数式処理を,Maxima の標準関数(名)を用いて処 理する方法について,その1つの試みを紹介する.以下に,実行例を示す.
実行例16
(%i1) f1(x) := x^2*on3(x,minf,0,oo) + (1-x^2)/2 *on3(x,0,1,oo)
+ (1-x)*on3(x,1,inf,oo)$ <--- on3関数式
(%i2) f0(x) := sin(x)$ <--- 一般式(on3関数を含まない式)
(%i3) f(x) := on3pw(f1(x)) + f0(x)$ <--- on3関数式をカプセル化した関数式
(%i4) define(df_direct(x), on3diff(f1(x),x,1) + diff(f0(x),x,1));
<--- 関数 f(x) の導関数を手動で求める
(%o4) df_direct(x) := 2 x on3(x, minf, 0, oo) - on3(x, 1, inf, co)
- x on3(x, 0, 1, oo) + cos(x)
(%i5) df_direct(1); <--- 導関数の検算
(%o5) cos(1) - 1
(%i6) define(df(x), diff(f(x),x)); <--- カプセル化関数の微分(標準関数 diff を用いて)
(%o6) df(x) := 2 x on3(x, minf, 0, oo) - on3(x, 1, inf, co)
- x on3(x, 0, 1, oo) + cos(x)
(%i7) df(1); <--- 導関数の検算
(%o7) cos(1) - 1
(%i8) define(F(x), integrate(f(x),x)); <--- カプセル化関数の不定積分
3 2
x on3(x, minf, 0, oc) (3 x - 6 x + 1) on3(x, 1, inf, oo)
(%o8) F(x) := ---------------------- - -----------------------------------
3 6
3
(x - 3 x) on3(x, 0, 1, oc)
- --------------------------- - cos(x)
6
(%i9) F(2) - F(-1); <--- 不定積分関数による定積分
1
(%o9) - cos(2) + cos(1) + -
6- Maxima 実行例16 不可
display2d:true$
f1(x) := x^2*on3(x,minf,0,oo) + (1-x^2)/2 *on3(x,0,1,oo)
+ (1-x)*on3(x,1,inf,oo)$
f0(x) := sin(x)$
f(x) := on3pw(f1(x)) + f0(x)$
define(df_direct(x), on3diff(f1(x),x,1) + diff(f0(x),x,1));
df_direct(1);
define(df(x), diff(f(x),x));
df(1);
define(F(x), integrate(f(x),x));
F(2) - F(-1);## ~/bin/go TMP/tmp_lang/chunk-25.mxl > TMP/tmp_lang/chunk-25.out 2>&1
## batch("/var/www/html/LANG/TMP/tmp_lang/chunk-25.mxl")
## read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-25.mxl
## display2d:true
## f1(x):=x^2*on3(x,minf,0,oo)+((1-x^2)/2)*on3(x,0,1,oo)+(1-x)*on3(x,1,inf,oo)
## f0(x):=sin(x)
## f(x):=on3pw(f1(x))+f0(x)
## define(df_direct(x),on3diff(f1(x),x,1)+diff(f0(x),x,1))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## df_direct(1)
## df_direct(1)
## define(df(x),diff(f(x),x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## df(1)
## df(1)
## define(F(x),integrate(f(x),x))
## Maxima encountered a Lisp error:
## Condition in MACSYMA-TOP-LEVEL [or a callee]: INTERNAL-SIMPLE-UNDEFINED-FUNCTION: Cell error on ^RULE1: Undefined function:
## Automatically continuing.
## To enable the Lisp debugger set *debugger-hook* to nil.
## F(2)-F(-1)
## F(2) - F(- 1)
## /var/www/html/LANG/TMP/tmp_lang/chunk-25.mxlここで,関数 on3pw() は関数名のみをもつ実体のない関数であり,on3 関数部をカプセル化する. また,Maxima の標準関数に on3 関数部を識別させるシンボルとして用いられる. この機能により,上記の実行例16の f(x) の様な形式で関数を定義すれば, on3 関数部を意識することなく, Maxima の標準関数 diff, integrate,等を用いた微分,積分, 等の操作が可能となる.
5 ライブラリの公開
本稿に示したライブラリ on3lib.mx を公開します.必要な方は筆者連絡先にメー ルを下さい.但し,開発途上である点をご承知下さい.また,ご批判,コメントは歓迎 します.なお,本ライブラリは,実行例13 の冒頭に表示されている環境 (Maxima 5.13.0 using CLISP 2.39, Linux (Vine)) で作成され, GNU Common Lisp (GCL 2.6.7) 上のMaxima 5.9.3 – 5.14.0 で 動作確認を行ないました.Windows XP 上では,日本語コード変換を必要 としますが,実行可能です.
ライブラリon3lib.mx内の例の実行
on3help()
on3help()$~/bin/go TMP/tmp_lang/chunk-26.mxl > TMP/tmp_lang/chunk-26.out 2>&1
batch("/var/www/html/LANG/TMP/tmp_lang/chunk-26.mxl")
read and interpret /var/www/html/LANG/TMP/tmp_lang/chunk-26.mxl
on3help()
=== on3lib.mx (定義域を伴った関数の数式操作) 一覧 ===
0. on3help() : on3関数の機能一覧
1. on3(z,z0,z1,arg) : on3関数(関数定義域)の定義[変数,下限,上限,開閉]
2. f2l(on3funcs) : on3関数式をon3リスト形式に変換する[多変数対応版]
3. l2f(on3list) : on3リスト形式をon3関数形式に変換する[多変数対応版]
4. on3simp(on3funcs) : on3関数式の積に関する簡約化(on3decompに組み込み)
5. on3decomp(funcs,[args]) : [多変数対応版]
on3関数式の和(差)において素な区間(領域)への分解表現を与える
6. on3std(on3func) : on3一般式の標準化
7. on3ev(on3func,arg) : 関数部に{factor,ratsimp,expand}を作用する
8. on3solve(funcs,vars) : on3関数式の求解[多変数対応版]
9. on3diff(func,var,p) : on3関数式の微分[多変数対応版]
10. on3integ(func,var,[args]) : on3関数式の積分[多変数対応版]
on3integ(func,var) : 不定積分関数(分布関数に対応)
on3integ(func,var,x0,x1) : 定積分値
11. on3chgvar2(funcs) : on3関数式f(x,y)を変換(t=x+y,u=y)した関数g(t,u)を返す
12. on3show(funcs) : on3関数式の表示[多変数対応版]
13. on3pw(funcs) : on3関数式のカプセル化
ex. on3_ex(), on3simp_ex(), on3std_ex(),
on3decomp_ex(), on3show_ex(), on3ev_ex(),
on3diff_ex(), on3integ_ex(), on3solve_ex(),
on3chgvar2_ex() on3pw_ex(),
ex. on3dim2_uni2() : 一様分布に従う独立確率変数の和の分布
on3dim2_exp2() : 指数分布に従う独立確率変数の和の分布
ex. on3test() : on3_ex, on3list_ex, on3simp_ex, on3decomp_ex の連続実行
---> 関数表示 dispfun(on3,on3simp,...) または grind(on3)
"/var/www/html/LANG/TMP/tmp_lang/chunk-26.mxl"